No CrossRef data available.
Article contents
FACTORIZATION OF MONOMORPHISMS OF A POLYNOMIAL ALGEBRA IN ONE VARIABLE
Published online by Cambridge University Press: 01 May 2008
Abstract
Let K[x] be a polynomial algebra in a variable x over a commutative 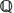 -algebra K, and Γ′ the monoid of K-algebra monomorphisms of K[x] of the type σ: x ↦ x+λ2x2 + . . . +λnxn, λi ∈ K, λn is a unit of K. It is proved that for each σ ∈ Γ′ there are only finitely many distinct decompositions σ = σ1. . .σs in Γ′. Moreover, each such decomposition is uniquely determined by the degrees of components: if σ = σ1. . . σs= τ1 . . . τs then σ1=τ1, λ. . ., σs=τs if and only if deg(σ1)=deg(τ1), . . ., deg(σs)=deg(τs). Explicit formulae are given for the components σi via the coefficients λj and the degrees deg(σk) (as an application of the inversion formula for polynomial automorphisms in several variables from [1]). In general, for a polynomial there are no formulae (in radicals) for its divisors (elementary Galois theory). Surprisingly, one can write such formulae where instead of the product of polynomials one considers their composition (as polynomial functions).
-algebra K, and Γ′ the monoid of K-algebra monomorphisms of K[x] of the type σ: x ↦ x+λ2x2 + . . . +λnxn, λi ∈ K, λn is a unit of K. It is proved that for each σ ∈ Γ′ there are only finitely many distinct decompositions σ = σ1. . .σs in Γ′. Moreover, each such decomposition is uniquely determined by the degrees of components: if σ = σ1. . . σs= τ1 . . . τs then σ1=τ1, λ. . ., σs=τs if and only if deg(σ1)=deg(τ1), . . ., deg(σs)=deg(τs). Explicit formulae are given for the components σi via the coefficients λj and the degrees deg(σk) (as an application of the inversion formula for polynomial automorphisms in several variables from [1]). In general, for a polynomial there are no formulae (in radicals) for its divisors (elementary Galois theory). Surprisingly, one can write such formulae where instead of the product of polynomials one considers their composition (as polynomial functions).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2008

