Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-15T11:33:31.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite abelian surface coverings†

Published online by Cambridge University Press:  18 May 2009

S. A. Jassim
S. A. Jassim
Affiliation:
11A Clarendon Road, Sketty, Swansea SA2 0SR, Wales
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a finite abelian group, and Y be a closed surface. The problems of classifying and enumerating the free and effective G-actions on Y modulo selfhomeomorphisms of Y and X = Y/G can be transferred into ones of classifying regular G-coverings on X. P. A. Smith [7], proved that for any prime number p there are pr(r–1)/2 equivalence classes of free (ℤp)r actions on Y provided that rℤgenus of X. This paper is devoted to the classification and the enumeration of regular G-covering surfaces, when G is any finite abelian group. Recently, A. Edmonds [2] classified the G-actions on closed surfaces by their G-bordism classes in the set 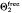(G) of free oriented G-cobordism classes of free oriented G-surfaces.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 25 , Issue 2 , July 1984 , pp. 207 - 218
Copyright
Copyright © Glasgow Mathematical Journal Trust 1984

References

REFERENCES

1.Birman, J. S., On Siegel's modular group, Math. Ann. 191 (1971), 59–68.CrossRefGoogle Scholar
2.Edmonds, A. L., Surface symmetry, Michigan Math. J. 29 (1982), 171–183.CrossRefGoogle Scholar
3.Hartley, B. and Hawkes, T. O., Rings modules and linear algebra (Chapman and Hall, 1970).Google Scholar
4.Jassim, S. A., Classifications of covering spaces (Ph.D. Thesis, University College of Swansea, 1980).Google Scholar
5.Lickorish, W. B. R., A finite set of generators for the homeotopy group of a 2-manifold, Proc. Cambridge Philos. Soc. 60 (1964), 769–778.CrossRefGoogle Scholar
6.Magnus, W., Karass, A. and Solitar, B., Combinatorial group theory, (John Wiley, 1966).Google Scholar
7.Smith, P. A., Abelian actions on 2-manifolds, Michigan Math. J. 14 (1967), 257–275.CrossRefGoogle Scholar