Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T07:02:45.641Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITENESS OF TOPOLOGICAL ENTROPY FOR LOCALLY COMPACT ABELIAN GROUPS

Part of: Topological and differentiable algebraic systems Topological dynamics Maps and general types of spaces defined by maps

Published online by Cambridge University Press:  26 February 2020

DIKRAN DIKRANJAN Open the ORCID record for DIKRAN DIKRANJAN [Opens in a new window] ,
ANNA GIORDANO BRUNO Open the ORCID record for ANNA GIORDANO BRUNO [Opens in a new window]  and
FRANCESCO G. RUSSO Open the ORCID record for FRANCESCO G. RUSSO [Opens in a new window]
DIKRAN DIKRANJAN
Affiliation:
Dipartimento di Scienze Matematiche, Informatiche e Fisiche, Università di Udine, Via delle Scienze 206, 33100Udine, Italy e-mails: dikran.dikranjan@uniud.it; anna.giordanobruno@uniud.it
ANNA GIORDANO BRUNO
Affiliation:
Dipartimento di Scienze Matematiche, Informatiche e Fisiche, Università di Udine, Via delle Scienze 206, 33100Udine, Italy e-mails: dikran.dikranjan@uniud.it; anna.giordanobruno@uniud.it
FRANCESCO G. RUSSO
Affiliation:
Department of Mathematics and Applied Mathematics, University of Cape Town, Private Bag X1, Rondebosch 7701, Cape Town, South Africa e-mail: francescog.russo@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the locally compact abelian groups in the class 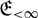${\mathfrak E_{ \lt \infty }}$ , that is, having only continuous endomorphisms of finite topological entropy, and in its subclass 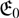$\mathfrak E_0$ , that is, having all continuous endomorphisms with vanishing topological entropy. We discuss the reduction of the problem to the case of periodic locally compact abelian groups, and then to locally compact abelian p-groups. We show that locally compact abelian p-groups of finite rank belong to 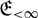${\mathfrak E_{ \lt \infty }}$ , and that those of them that belong to 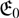$\mathfrak E_0$ are precisely the ones with discrete maximal divisible subgroup. Furthermore, the topological entropy of endomorphisms of locally compact abelian p-groups of finite rank coincides with the logarithm of their scale. The backbone of the paper is the Addition Theorem for continuous endomorphisms of locally compact abelian groups. Various versions of the Addition Theorem are established in the paper and used in the proofs of the main results, but its validity in the general case remains an open problem.

MSC classification

Primary: 22A05: Structure of general topological groups 37B40: Topological entropy
Secondary: 54C70: Entropy
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 1 , January 2021 , pp. 81 - 105
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, R. L., Konheim, A. G. and McAndrew, M. H., Topological entropy, Trans. Amer. Math. Soc. 114 (1965), 309–319.Google Scholar
Alcaraz, D., Dikranjan, D. and Sanchis, M., Bowen’s entropy for endomorphisms of totally bounded abelian groups, in Descriptive topology and functional analysis (Ferrando, J. C. and López-Pellicer, M., Editors), Springer Proceedings in Mathematics & Statistics, vol. 80 (Springer, Cham, 2014), 143–162.Google Scholar
Baumgartner, U. and Willis, G. A., Contraction groups and scales of automorphisms of totally disconnected locally compact groups, Israel J. Math. 142 (2004), 221–248.Google Scholar
Berlai, F., Dikranjan, D. and Giordano Bruno, A., Scale function vs Topological entropy, Topology Appl. 160 (2013), 2314–2334.CrossRefGoogle Scholar
Bowen, R., Entropy for group endomorphisms and homogeneous spaces, Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
Braconnier, J., Sur les groupes topologiques localement compacts, J. Math. Pures Appl. 27(9)(1948) 1–85.Google Scholar
Dikranjan, D. and Giordano Bruno, A., Topological entropy and algebraic entropy for group endomorphisms, in Proceedings ICTA2011 Islamabad, Pakistan, July 4–10, 2011 (Cambridge Scientific Publishers, 2012), 133–214.Google Scholar
Dikranjan, D. and Giordano Bruno, A., The Bridge Theorem for totally disconnected LCA groups, Topology Appl. 169 (2014), 21–32.CrossRefGoogle Scholar
Dikranjan, D. and Giordano Bruno, A., Entropy on abelian groups, Adv. Math. 298 (2016), 612–653.CrossRefGoogle Scholar
Dikranjan, D., Goldsmith, B., Salce, L. and Zanardo, P., Algebraic entropy of endomorphisms of abelian groups, Trans. Amer. Math. Soc. 361 (2009), 3401–3434.CrossRefGoogle Scholar
Dikranjan, D., Iv. Prodanov and Stoyanov, L., Topological groups: character, dualities and minimal group topologies, Pure and Applied Mathematics, vol. 130 (Marcel Dekker Inc., New York-Basel, 1989).Google Scholar
Dikranjan, D. and Sanchis, M., Dimension and entropy in compact topological groups, J. Math. Anal. Appl. 476(2) (2019), 337–366.CrossRefGoogle Scholar
Dikranjan, D., Sanchis, M. and Virili, S., New and old facts about entropy in uniform spaces and topological groups, Topology Appl. 159 (2012), 1916–1942.CrossRefGoogle Scholar
Giordano Bruno, A. and Virili, S., Algebraic Yuzinvinski Formula, J. Alg. 423 (2015), 114–147.CrossRefGoogle Scholar
Giordano Bruno, A. and Virili, S., On the Algebraic Yuzvinski formula, Topololgical Alg. Appl. 3 (2015), 86–103.Google Scholar
Giordano Bruno, A. and Virili, S., Topological entropy in totally disconnected locally compact groups, Ergodic Theor. Dyn. Sys. 37 (2017), 2163–2186.CrossRefGoogle Scholar
Glöckner, H., Scale functions on p-adic Lie groups, Manuscripta Math. 97 (1998), 205–215.Google Scholar
Herfort, W., Hofmann, K. H. and Russo, F. G., Periodic locally compact groups, Stud. Math. 71 (2019), De Gruyter.CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A., Abstract harmonic analysis I (Springer-Verlag, Berlin-Heidelberg-New York, 1963).Google Scholar
Hofmann, K. H. and Morris, S., The structure of compact groups (de Gruyter, Berlin, 2006).CrossRefGoogle Scholar
Hood, B. M., Topological entropy and uniform spaces, J. London Math. Soc. 8(2) (1974), 633–641.CrossRefGoogle Scholar
Leedham-Green, C. R. and McKay, S., The structure of groups of prime power order, LMSM 27 (Oxford University Press, Oxford, 2002).Google Scholar
Lehmer, D. H., Factorization of certain cyclotomic functions, Ann. Math. 34 (1933), 461–479.CrossRefGoogle Scholar
Lind, D. and Ward, T., Automorphisms of solenoids of p-adic entropy, Ergod. Theory Dyn. Sys. 8 (1988), 411–419.CrossRefGoogle Scholar
Peters, J., Entropy of automorphisms on L.C.A. groups, Pacific J. Math. 96(2) (1981), 475–488.CrossRefGoogle Scholar
Schmidt, K., Dynamical systems of algebraic origin, Progress in Mathematics, vol. 128 (Birkhäuser Zentralblatt Verlag, Basel, 1995).Google Scholar
van Dantzig, D., Studien over topologische Algebra, Dissertation (Amsterdam, 1931).Google Scholar
Virili, S., Entropy for endomorphisms of LCA groups, Topology Appl. 159(9) (2012). 2546–2556.CrossRefGoogle Scholar
Walters, P., An introduction to ergodic theory (Springer, Berlin, 1969).Google Scholar
Willis, G. A., The scale and tidy subgroups for endomorphisms of totally disconnected locally compact groups, Math. Ann. 361 (2015), 403–442.Google Scholar
Yuzvinski, S., Metric properties of endomorphisms of compact groups, Izv. Acad. Nauk SSSR Ser. Mat. 29 (1965), 1295–1328 (in Russian). English Translation: Amer. Math. Soc. Transl. 66(2) (1968), 63–98.Google Scholar