Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wright, J. D. Maitland
1969.
A lifting theorem for Boolean ?-algebras.
Mathematische Zeitschrift,
Vol. 112,
Issue. 5,
p.
326.
Wright, J. D. Maitland
1970.
A decomposition theorem.
Mathematische Zeitschrift,
Vol. 115,
Issue. 5,
p.
387.
1981.
Foundations of Stochastic Analysis.
p.
283.

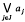 and the greatest lower bound by
and the greatest lower bound by 