Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
BAUES, HANS-JOACHIM
and
MIKHAILOV, ROMAN
2008.
INTERSECTION OF SUBGROUPS IN FREE GROUPS AND HOMOTOPY GROUPS.
International Journal of Algebra and Computation,
Vol. 18,
Issue. 05,
p.
803.
Михайлов, Роман Валерьевич
and
Mikhailov, Roman Valer'evich
2014.
Гомотопические и комбинаторные аспекты теории нормальных рядов в группах.
Современные проблемы математики,
Vol. 18,
Issue. ,
p.
3.
Mikhailov, R.
2014.
Homotopical and combinatorial aspects of the theory of normal series in groups.
Proceedings of the Steklov Institute of Mathematics,
Vol. 286,
Issue. S1,
p.
1.
Kulikova, O. V.
2018.
On Independent Families of Normal Subgroups in Free Groups.
Journal of Mathematical Sciences,
Vol. 233,
Issue. 1,
p.
125.

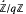 /q for any non-negative integer
/q for any non-negative integer 