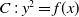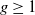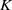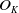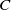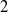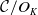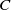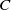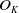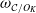1. Introduction
The purpose of this paper is to construct regular models of hyperelliptic curves and to describe a basis of integral differentials attached to them. Moreover, we want these constructions explicit and easy to compute.
1.1. Overview
To describe the arithmetic of curves over global fields, for example in the study of the Birch & Swinnerton-Dyer conjecture, it is essential to understand regular models and integral differentials over all primes, including those with very bad reduction. Constructing regular models of curves over discrete valuation rings is not an easy problem, even in the hyperelliptic curve case. In fact, there is no practical algorithm able to determine a model, unless the genus of the curve is
![]() $1$
or we have some tameness or nondegeneracy hypothesis.
$1$
or we have some tameness or nondegeneracy hypothesis.
One possible approach to tackle this problem is giving a full classification of possible regular models in a fixed genus, as done by the Kodaira–Néron [Reference Kodaira7, Reference Néron19] and Namikawa–Ueno [Reference Liu10, Reference Namikawa and Ueno18] classifications for curves of genera
![]() $1$
and
$1$
and
![]() $2$
, respectively. However, this strategy seems impractical in general, since the number of models grows fast with the genus. Recently, new approaches based on clusters [Reference Dokchitser, Dokchitser, Maistret and Morgan14], Newton polytopes [Reference Dokchitser1], and MacLane valuations [Reference Obus and Wewers21], have been developed (see Section 1.5 for more detail).
$2$
, respectively. However, this strategy seems impractical in general, since the number of models grows fast with the genus. Recently, new approaches based on clusters [Reference Dokchitser, Dokchitser, Maistret and Morgan14], Newton polytopes [Reference Dokchitser1], and MacLane valuations [Reference Obus and Wewers21], have been developed (see Section 1.5 for more detail).
On one side, clusters define nice and clear invariants from which one can extract information on the local arithmetic of hyperelliptic curves. Such invariants turn out to be particularly useful from a Galois theoretical point of view. However, for describing regular models, restrictions on the reduction type of the curve and on the residue characteristic of its base field [Reference Faraggi and Nowell5, Reference Dokchitser, Dokchitser, Maistret and Morgan14] need to be imposed. On the other side, Newton polytopes and MacLane valuations have a potential to solve the problem in general, but the respective constructions are more algorithmic and so do not give the result in closed form. Furthermore, they often depend on the chosen equation rather than on the curve itself.
In this paper, we present a new approach that preserves both positive aspects from the above and provides a link between the two sides. We describe a model from simple invariants defined from what we call rational cluster picture (Definition 1.10). This object modifies the theory in [Reference Dokchitser, Dokchitser, Maistret and Morgan14] and appears to be more suitable for our purpose (see Section 1.3). In fact, the rational cluster picture also carries intrinsic connections with the other presented approaches, as it is closely related to Newton polygons and to degree
![]() $1$
MacLane valuations (see [Reference Fernández, Guárdia, Montes and Nart3]). When these valuations are enough to describe a regular model we say that the curve has an almost rational cluster picture (Definition 1.1; see also Corollary 3.29, Proposition 3.31). It turns out that the approach even works in residue characteristic 2, under an extra assumption that the curve is
$1$
MacLane valuations (see [Reference Fernández, Guárdia, Montes and Nart3]). When these valuations are enough to describe a regular model we say that the curve has an almost rational cluster picture (Definition 1.1; see also Corollary 3.29, Proposition 3.31). It turns out that the approach even works in residue characteristic 2, under an extra assumption that the curve is
![]() $y$
-regular (Definition 1.4). Our main result is:
$y$
-regular (Definition 1.4). Our main result is:
Let
![]() $K$
be a complete
Footnote 1 discretely valued field with
$K$
be a complete
Footnote 1 discretely valued field with
![]() $\textrm{char}(K)\neq 2$
, and let
$\textrm{char}(K)\neq 2$
, and let
![]() $K^{nr}$
be its maximal unramified extension. Let
$K^{nr}$
be its maximal unramified extension. Let
![]() $C/K$
be a hyperelliptic curve, having an almost rational cluster picture over
$C/K$
be a hyperelliptic curve, having an almost rational cluster picture over
![]() $K^{nr}$
. If the residue characteristic of
$K^{nr}$
. If the residue characteristic of
![]() $K$
is
$K$
is
![]() $2$
, assume that
$2$
, assume that
![]() $C_{K^{nr}}$
is
$C_{K^{nr}}$
is
![]() $y$
-regular. Then via the rational cluster picture we determine:
$y$
-regular. Then via the rational cluster picture we determine:
-
(i) the minimal regular model with normal crossings
 $\mathcal{C}^{\textrm{min}}$
,
$\mathcal{C}^{\textrm{min}}$
, -
(ii) a basis of integral differentials of
 $C$
.
$C$
.
This result applies to a wide class of curves, covering wild cases and base fields with even residue characteristic. For example, if
![]() $g=2$
, then
$g=2$
, then
![]() $107$
out of
$107$
out of
![]() $120$
Namikawa-Ueno types [Reference Namikawa and Ueno18] arise from hyperelliptic curves satisfying the conditions of our theorem. In addition, the author believes it has a potential to solve the problem in general. Heuristically speaking, the rational clusters invariants are expected to extend to general MacLane valuations. This approach could eventually lead to a full characterisation of minimal models with normal crossings of hyperelliptic curves (over any discretely valued field).
$120$
Namikawa-Ueno types [Reference Namikawa and Ueno18] arise from hyperelliptic curves satisfying the conditions of our theorem. In addition, the author believes it has a potential to solve the problem in general. Heuristically speaking, the rational clusters invariants are expected to extend to general MacLane valuations. This approach could eventually lead to a full characterisation of minimal models with normal crossings of hyperelliptic curves (over any discretely valued field).
1.2. Main results
We will now present (a simplified version of) the main results of this paper. We will then illustrate them with an explicit example in Section 1.4.
Let
![]() $K$
be a complete discretely valued field of residue characteristic
$K$
be a complete discretely valued field of residue characteristic
![]() $p$
, with normalised discrete valuation
$p$
, with normalised discrete valuation
![]() $v$
and ring of integers
$v$
and ring of integers
![]() $O_K$
. We require
$O_K$
. We require
![]() $\textrm{char}(K)$
to be not
$\textrm{char}(K)$
to be not
![]() $2$
, but we allow
$2$
, but we allow
![]() $p=2$
and
$p=2$
and
![]() $p=0$
. In this subsection we will assume for simplicity that
$p=0$
. In this subsection we will assume for simplicity that
![]() $K=K^{nr}$
. Extend the valuation
$K=K^{nr}$
. Extend the valuation
![]() $v$
to an algebraic closure
$v$
to an algebraic closure
![]() $\bar{K}$
of
$\bar{K}$
of
![]() $K$
. Let
$K$
. Let
![]() $C/K$
be a hyperelliptic curve, that is a geometrically connected smooth projective curve, double cover of
$C/K$
be a hyperelliptic curve, that is a geometrically connected smooth projective curve, double cover of
![]() ${\mathbb{P}}^1_K$
. Let
${\mathbb{P}}^1_K$
. Let
![]() $g$
be the genus of
$g$
be the genus of
![]() $C$
. Assume
$C$
. Assume
![]() $g\geq 1$
. Fix a Weierstrass equation
$g\geq 1$
. Fix a Weierstrass equation
Let
![]() $\mathfrak{R}$
be the set of roots of
$\mathfrak{R}$
be the set of roots of
![]() $f$
in
$f$
in
![]() $\bar{K}$
. Thus
$\bar{K}$
. Thus
For any
![]() $r,r'\in \mathfrak{R}$
, with
$r,r'\in \mathfrak{R}$
, with
![]() $r\neq r'$
, denote by
$r\neq r'$
, denote by
![]() $\mathcal{D}_{r,r^{\prime}}$
the smallest
$\mathcal{D}_{r,r^{\prime}}$
the smallest
![]() $v$
-adic disc containing
$v$
-adic disc containing
![]() $r$
and
$r$
and
![]() $r'$
.
$r'$
.
Definition 1.1 (Definition 3.26). We say that
![]() $C$
has an almost rational cluster picture if for any roots
$C$
has an almost rational cluster picture if for any roots
![]() $r,r'\in \mathfrak{R}$
with
$r,r'\in \mathfrak{R}$
with
![]() $r\neq r'$
, either
$r\neq r'$
, either
-
(a)
 $\mathcal{D}_{r,r^{\prime}}\cap K\neq \varnothing$
, or
$\mathcal{D}_{r,r^{\prime}}\cap K\neq \varnothing$
, or
-
(b)
 $p\gt 0$
and
$p\gt 0$
and
 $|\mathcal{D}_{r,r^{\prime}}\cap \mathfrak{R}|\leq |v(r-w)|_p$
for some
$|\mathcal{D}_{r,r^{\prime}}\cap \mathfrak{R}|\leq |v(r-w)|_p$
for some
 $w\in K$
,
$w\in K$
,
where
![]() $|\cdot |_p$
denotes the canonical
$|\cdot |_p$
denotes the canonical
![]() $p$
-adic absolute value on
$p$
-adic absolute value on
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Definition 1.2.
A rational cluster is a non-empty subset
![]() $\mathfrak{s}\subset \mathfrak{R}$
of the form
$\mathfrak{s}\subset \mathfrak{R}$
of the form
![]() $\mathcal{D}\cap \mathfrak{R}$
, where
$\mathcal{D}\cap \mathfrak{R}$
, where
![]() $\mathcal{D}$
is a
$\mathcal{D}$
is a
![]() $v$
-adic disc
$v$
-adic disc
![]() $\mathcal{D}=\{x\in \bar{K}\mid v(x-w)\geq \rho \}$
for some
$\mathcal{D}=\{x\in \bar{K}\mid v(x-w)\geq \rho \}$
for some
![]() $w\in K$
and
$w\in K$
and
![]() $\rho \in \mathbb{Q}$
. We denote by
$\rho \in \mathbb{Q}$
. We denote by
![]() $\Sigma _K$
the set of rational clusters.
$\Sigma _K$
the set of rational clusters.
In the following definition we introduce most of the notation and quantities, associated with rational clusters, needed in order to state our main theorems.
Definition 1.3.
For any
![]() $\mathfrak{s}\in \Sigma _K$
we say:
$\mathfrak{s}\in \Sigma _K$
we say:
|
|
|
|
|
|
|
|
|
|
|
|
Moreover, we write
![]() $\mathfrak{s}^{\prime}\lt \mathfrak{s}$
, or
$\mathfrak{s}^{\prime}\lt \mathfrak{s}$
, or
![]() $\mathfrak{s}=P(\mathfrak{s}^{\prime})$
, for a child
$\mathfrak{s}=P(\mathfrak{s}^{\prime})$
, for a child
![]() $\mathfrak{s}^{\prime}\in \Sigma _K$
of
$\mathfrak{s}^{\prime}\in \Sigma _K$
of
![]() $\mathfrak{s}$
, and
$\mathfrak{s}$
, and
![]() $r\wedge \mathfrak{s}$
for the smallest rational cluster containing the root
$r\wedge \mathfrak{s}$
for the smallest rational cluster containing the root
![]() $r\in \mathfrak{R}$
and
$r\in \mathfrak{R}$
and
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
Let
![]() $\Sigma _K$
be the set of proper rational clusters. For any
$\Sigma _K$
be the set of proper rational clusters. For any
![]() $\mathfrak{s}\in \Sigma _K$
, define its radius
$\mathfrak{s}\in \Sigma _K$
, define its radius
and the following quantities:
|
|
denominator of
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 if
|
Definition 1.4 (Definition 4.10). We say that the hyperelliptic curve
![]() $C$
is
$C$
is
![]() $y$
-regular if either
$y$
-regular if either
![]() $p\neq 2$
or
$p\neq 2$
or
![]() $D_{\mathfrak{s}}=1$
for any
$D_{\mathfrak{s}}=1$
for any
![]() $\mathfrak{s}\in \Sigma _K$
.
$\mathfrak{s}\in \Sigma _K$
.
Definition 1.5.
Let
![]() $\mathfrak{s}\in \Sigma _K$
and let
$\mathfrak{s}\in \Sigma _K$
and let
![]() $c\in \{0,\dots,b_{\mathfrak{s}}-1\}$
such that
$c\in \{0,\dots,b_{\mathfrak{s}}-1\}$
such that
![]() $c\rho _{\mathfrak{s}}-\frac{1}{b_{\mathfrak{s}}}\in \mathbb{Z}$
. Define
$c\rho _{\mathfrak{s}}-\frac{1}{b_{\mathfrak{s}}}\in \mathbb{Z}$
. Define
where
![]() $\varnothing \lt \mathfrak{s}$
if
$\varnothing \lt \mathfrak{s}$
if
![]() $\mathfrak{s}$
is minimal and
$\mathfrak{s}$
is minimal and
![]() $p_{\mathfrak{s}}^0=2$
.
$p_{\mathfrak{s}}^0=2$
.
The genus
![]() $g(\mathfrak{s})$
of a rational cluster
$g(\mathfrak{s})$
of a rational cluster
![]() $\mathfrak{s}\in \Sigma _K$
is defined as follows:
$\mathfrak{s}\in \Sigma _K$
is defined as follows:
-
If
 $D_{\mathfrak{s}}=1$
, then
$D_{\mathfrak{s}}=1$
, then
 $g(\mathfrak{s})=0$
.
$g(\mathfrak{s})=0$
. -
If
 $D_{\mathfrak{s}}=2$
, then
$D_{\mathfrak{s}}=2$
, then
 $2g(\mathfrak{s})+1$
or
$2g(\mathfrak{s})+1$
or
 $2g(\mathfrak{s})+2$
equals
$2g(\mathfrak{s})+2$
equals
 $\dfrac{|\mathfrak{s}|-\sum _{\mathfrak{s}^{\prime}\lt \mathfrak{s}}|\mathfrak{s}^{\prime}|}{b_{\mathfrak{s}}}+|\tilde{\mathfrak{s}}|$
.
$\dfrac{|\mathfrak{s}|-\sum _{\mathfrak{s}^{\prime}\lt \mathfrak{s}}|\mathfrak{s}^{\prime}|}{b_{\mathfrak{s}}}+|\tilde{\mathfrak{s}}|$
.
Notation 1.6.
Let
![]() $\alpha \in \mathbb{Z}_+$
,
$\alpha \in \mathbb{Z}_+$
,
![]() $a,b\in \mathbb{Q}$
, with
$a,b\in \mathbb{Q}$
, with
![]() $a\gt b$
, and fix
$a\gt b$
, and fix
![]() $\frac{n_i}{d_i}\in \mathbb{Q}$
so that
$\frac{n_i}{d_i}\in \mathbb{Q}$
so that
and
![]() $r$
minimal. We write
$r$
minimal. We write
![]() ${\mathbb{P}}^1(\alpha,a,b)$
for a chain of
${\mathbb{P}}^1(\alpha,a,b)$
for a chain of
![]() ${\mathbb{P}}^1$
s (Notation 4.16) of length
${\mathbb{P}}^1$
s (Notation 4.16) of length
![]() $r$
and multiplicities
$r$
and multiplicities
![]() $\alpha d_i,\dots,\alpha d_r$
. Denote by
$\alpha d_i,\dots,\alpha d_r$
. Denote by
![]() ${\mathbb{P}}^1(\alpha,a)$
the chain
${\mathbb{P}}^1(\alpha,a)$
the chain
![]() ${\mathbb{P}}^1(\alpha,a,\lfloor \alpha a-1\rfloor/\alpha )$
.
${\mathbb{P}}^1(\alpha,a,\lfloor \alpha a-1\rfloor/\alpha )$
.
The following theorem describes the special fibre of a regular model of
![]() $C$
with strict normal crossings.Footnote 2 It follows from a more general result constructing a proper flat model of
$C$
with strict normal crossings.Footnote 2 It follows from a more general result constructing a proper flat model of
![]() $C$
unconditionally (Theorem 4.18). For the special fibre
$C$
unconditionally (Theorem 4.18). For the special fibre
![]() $\mathcal{C}^{\textrm{min}}_s$
of the minimal regular model with normal crossings, the reader can refer to Theorem 4.23, where we also describe a defining equation for all components of
$\mathcal{C}^{\textrm{min}}_s$
of the minimal regular model with normal crossings, the reader can refer to Theorem 4.23, where we also describe a defining equation for all components of
![]() $\mathcal{C}_s^{\textrm{min}}$
and discuss the Galois action (for general
$\mathcal{C}_s^{\textrm{min}}$
and discuss the Galois action (for general
![]() $K$
). Finally, note that all these models are constructed in Section 5 by giving an explicit open affine cover (see Sections 5.1–5.3).
$K$
). Finally, note that all these models are constructed in Section 5 by giving an explicit open affine cover (see Sections 5.1–5.3).
Theorem 1.7 (Regular SNC model). Suppose
![]() $C$
is
$C$
is
![]() $y$
-regular and has almost rational cluster picture. Then we can explicitly construct a regular model with strict normal crossings
$y$
-regular and has almost rational cluster picture. Then we can explicitly construct a regular model with strict normal crossings
![]() $\mathcal{C}/O_{K}$
of
$\mathcal{C}/O_{K}$
of
![]() $C$
(Sections 5.1–5.3
). Its special fibre
$C$
(Sections 5.1–5.3
). Its special fibre
![]() $\mathcal{C}_s/k$
is given as follows.
$\mathcal{C}_s/k$
is given as follows.
-
(1) Every
 $\mathfrak{s}\in \Sigma _K$
gives a
$\mathfrak{s}\in \Sigma _K$
gives a
 $1$
-dimensional closed subscheme
$1$
-dimensional closed subscheme
 $\Gamma _{\mathfrak{s}}$
of multiplicity
$\Gamma _{\mathfrak{s}}$
of multiplicity
 $m_{\mathfrak{s}}$
. If
$m_{\mathfrak{s}}$
. If
 $\mathfrak{s}$
is übereven and
$\mathfrak{s}$
is übereven and
 $\epsilon _{\mathfrak{s}}$
is even, then
$\epsilon _{\mathfrak{s}}$
is even, then
 $\Gamma _{\mathfrak{s}}$
is the disjoint union of
$\Gamma _{\mathfrak{s}}$
is the disjoint union of
 $\Gamma _{\mathfrak{s}}^{-}\simeq{\mathbb{P}}^1$
and
$\Gamma _{\mathfrak{s}}^{-}\simeq{\mathbb{P}}^1$
and
 $\Gamma _{\mathfrak{s}}^{+}\simeq{\mathbb{P}}^1$
, otherwise
$\Gamma _{\mathfrak{s}}^{+}\simeq{\mathbb{P}}^1$
, otherwise
 $\Gamma _{\mathfrak{s}}$
is a smooth geometrically integral curve of genus
$\Gamma _{\mathfrak{s}}$
is a smooth geometrically integral curve of genus
 $g(\mathfrak{s})$
(write
$g(\mathfrak{s})$
(write
 $\Gamma _{\mathfrak{s}}^{-}=\Gamma _{\mathfrak{s}}^{+}=\Gamma _{\mathfrak{s}}$
in this case).
$\Gamma _{\mathfrak{s}}^{-}=\Gamma _{\mathfrak{s}}^{+}=\Gamma _{\mathfrak{s}}$
in this case).
-
(2) Every
 $\mathfrak{s}\in \Sigma _K$
with
$\mathfrak{s}\in \Sigma _K$
with
 $D_{\mathfrak{s}}=1$
gives
$D_{\mathfrak{s}}=1$
gives
 $(|\mathfrak{s}|-\sum _{\mathfrak{s}^{\prime}\in \Sigma _K,\,\mathfrak{s}^{\prime}\lt \mathfrak{s}}|\mathfrak{s}^{\prime}|+p_{\mathfrak{s}}^0-2)/b_{\mathfrak{s}}$
open-ended
$(|\mathfrak{s}|-\sum _{\mathfrak{s}^{\prime}\in \Sigma _K,\,\mathfrak{s}^{\prime}\lt \mathfrak{s}}|\mathfrak{s}^{\prime}|+p_{\mathfrak{s}}^0-2)/b_{\mathfrak{s}}$
open-ended
 ${\mathbb{P}}^1$
s of multiplicity
${\mathbb{P}}^1$
s of multiplicity
 $b_{\mathfrak{s}}$
from
$b_{\mathfrak{s}}$
from
 $\Gamma _{\mathfrak{s}}$
.
$\Gamma _{\mathfrak{s}}$
. -
(3) Finally, for any
 $\mathfrak{s}\in \Sigma _K$
draw the following chains of
$\mathfrak{s}\in \Sigma _K$
draw the following chains of
 ${\mathbb{P}}^1$
s:
${\mathbb{P}}^1$
s:
| Conditions | Chain | From | To |
|
|
|
|
open-ended |
|
|
|
|
open-ended |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
open-ended |
|
|
|
|
open-ended |
Definition 1.8.
For any
![]() $\mathfrak{s}\in \Sigma _K$
, an element
$\mathfrak{s}\in \Sigma _K$
, an element
![]() $w_{\mathfrak{s}}\in K$
is called rational centre of
$w_{\mathfrak{s}}\in K$
is called rational centre of
![]() $\mathfrak{s}$
if
$\mathfrak{s}$
if
![]() $\min _{r\in \mathfrak{s}}v(r-w_{\mathfrak{s}})=\rho _{\mathfrak{s}}$
.
$\min _{r\in \mathfrak{s}}v(r-w_{\mathfrak{s}})=\rho _{\mathfrak{s}}$
.
If
![]() $\mathfrak{s}^{\prime}\lt \mathfrak{s}$
and
$\mathfrak{s}^{\prime}\lt \mathfrak{s}$
and
![]() $w_{\mathfrak{s}^{\prime}}$
is a rational centre of
$w_{\mathfrak{s}^{\prime}}$
is a rational centre of
![]() $\mathfrak{s}^{\prime}$
, then
$\mathfrak{s}^{\prime}$
, then
![]() $w_{\mathfrak{s}^{\prime}}$
is also a rational centre of
$w_{\mathfrak{s}^{\prime}}$
is also a rational centre of
![]() $\mathfrak{s}$
. For any minimal rational cluster
$\mathfrak{s}$
. For any minimal rational cluster
![]() $\mathfrak{s}^{\prime}$
fix a rational centre
$\mathfrak{s}^{\prime}$
fix a rational centre
![]() $w_{\mathfrak{s}^{\prime}}$
. For any
$w_{\mathfrak{s}^{\prime}}$
. For any
![]() $\mathfrak{s}\in \Sigma _K$
fix
$\mathfrak{s}\in \Sigma _K$
fix
![]() $w_{\mathfrak{s}}=w_{\mathfrak{s}^{\prime}}$
for some minimal rational cluster
$w_{\mathfrak{s}}=w_{\mathfrak{s}^{\prime}}$
for some minimal rational cluster
![]() $\mathfrak{s}^{\prime}\subseteq \mathfrak{s}$
.
$\mathfrak{s}^{\prime}\subseteq \mathfrak{s}$
.
The following result gives a basis of integral differentials when
![]() $K=K^{nr}$
. In Theorem 6.4 we extend it to the case
$K=K^{nr}$
. In Theorem 6.4 we extend it to the case
![]() $K\neq K^{nr}$
.
$K\neq K^{nr}$
.
Theorem 1.9 (Theorem 6.3). Suppose
![]() $C$
is
$C$
is
![]() $y$
-regular and has almost rational cluster picture. For
$y$
-regular and has almost rational cluster picture. For
![]() $i=0,\dots,g-1$
, inductively
$i=0,\dots,g-1$
, inductively
-
(i) define
 $e_i\;:\!=\;\displaystyle \max _{\mathfrak{t}\in \Sigma _K}\bigg \{\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{\mathfrak{s}_j\wedge \mathfrak{t}}\bigg \}$
;
$e_i\;:\!=\;\displaystyle \max _{\mathfrak{t}\in \Sigma _K}\bigg \{\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{\mathfrak{s}_j\wedge \mathfrak{t}}\bigg \}$
; -
(ii) let
 $\Sigma _i=\displaystyle \bigg \{\mathfrak{t}\in \Sigma _K\mid \,e_i=\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{\mathfrak{s}_j\wedge \mathfrak{t}}\bigg \}$
;
$\Sigma _i=\displaystyle \bigg \{\mathfrak{t}\in \Sigma _K\mid \,e_i=\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{\mathfrak{s}_j\wedge \mathfrak{t}}\bigg \}$
; -
(iii) choose a maximal element
 $\mathfrak{s}_i$
of
$\mathfrak{s}_i$
of
 $\Sigma _i$
freely.
$\Sigma _i$
freely.
Then a basis of integral differentials is given by
 \begin{align*} \mu _i=\pi ^{\lfloor e_i\rfloor }\prod _{j=0}^{i-1}(x-w_{\mathfrak{s}_j})\frac{dx}{2y},\qquad i=0,\dots,g-1. \end{align*}
\begin{align*} \mu _i=\pi ^{\lfloor e_i\rfloor }\prod _{j=0}^{i-1}(x-w_{\mathfrak{s}_j})\frac{dx}{2y},\qquad i=0,\dots,g-1. \end{align*}
Note that given
![]() $e_i$
as in the previous theorem, the sum
$e_i$
as in the previous theorem, the sum
![]() $\sum _{i=0}^{g-1}\lfloor e_i \rfloor$
is the quantity, often denoted by
$\sum _{i=0}^{g-1}\lfloor e_i \rfloor$
is the quantity, often denoted by
![]() $v({\omega ^\circ }/{\omega })$
, appearing in the period in the Birch and Swinnerton-Dyer conjecture (for more details see [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell4], [Reference van Bommel25, §1.3]).
$v({\omega ^\circ }/{\omega })$
, appearing in the period in the Birch and Swinnerton-Dyer conjecture (for more details see [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell4], [Reference van Bommel25, §1.3]).
1.3. Rational cluster picture
In this subsection we define the rational cluster picture and compare it with the classical cluster picture defined in [Reference Dokchitser, Dokchitser, Maistret and Morgan14]. We will show, via a simple example, in which sense the new object we introduce appears to be more suitable for the study of regular models.
Definition 1.10 (Definition 3.9). Let
![]() $K$
and
$K$
and
![]() $C$
as before. The rational cluster picture of
$C$
as before. The rational cluster picture of
![]() $C$
is the collection of its rational clusters
$C$
is the collection of its rational clusters
![]() $\Sigma _K$
together with their radii.
$\Sigma _K$
together with their radii.
Example 1.11.
Let
![]() $p$
be any prime number and set
$p$
be any prime number and set
![]() $K=\mathbb{Q}_p^{nr}$
. Let
$K=\mathbb{Q}_p^{nr}$
. Let
![]() $E_p/\mathbb{Q}_p^{nr}$
given by
$E_p/\mathbb{Q}_p^{nr}$
given by
![]() $y^2=x^3-p$
. Then
$y^2=x^3-p$
. Then
![]() $E_p$
is an elliptic curve with Kodaira-Néron reduction type II. Therefore, the minimal regular model (with normal crossings) of
$E_p$
is an elliptic curve with Kodaira-Néron reduction type II. Therefore, the minimal regular model (with normal crossings) of
![]() $E_p$
does not depend on
$E_p$
does not depend on
![]() $p$
. This is in accordance with the fact that the rational cluster picture of
$p$
. This is in accordance with the fact that the rational cluster picture of
![]() $E_p$
is the same for all
$E_p$
is the same for all
![]() $p$
. Indeed, the set of roots of the polynomial
$p$
. Indeed, the set of roots of the polynomial
![]() $x^3-p$
is
$x^3-p$
is
![]() $\mathfrak{R}=\{\sqrt [3]{p}, \zeta _3\sqrt [3]{p}, \zeta _3^2\sqrt [3]{p}\}$
, where
$\mathfrak{R}=\{\sqrt [3]{p}, \zeta _3\sqrt [3]{p}, \zeta _3^2\sqrt [3]{p}\}$
, where
![]() $\zeta _3$
is a primitive
$\zeta _3$
is a primitive
![]() $3$
rd of unity. Hence the rational cluster picture of
$3$
rd of unity. Hence the rational cluster picture of
![]() $E_p$
is
$E_p$
is

where we denoted with bullet points the roots in
![]() $\mathfrak{R}$
, with a surrounding oval the only rational cluster
$\mathfrak{R}$
, with a surrounding oval the only rational cluster
![]() $\mathfrak{R}$
, and with the subscript the radius
$\mathfrak{R}$
, and with the subscript the radius
![]() $\rho _{\mathfrak{R}}$
of
$\rho _{\mathfrak{R}}$
of
![]() $\mathfrak{R}$
.
$\mathfrak{R}$
.
A different behaviour is observed when we consider the cluster picture [Reference Dokchitser, Dokchitser, Maistret and Morgan14
, Definition 1.26] of
![]() $E_p$
, collection of its clusters together with their depths. The cluster picture of
$E_p$
, collection of its clusters together with their depths. The cluster picture of
![]() $E_p$
is
$E_p$
is

where the subscripts represent the depth of the cluster
![]() $\mathfrak{R}$
. It does depend on
$\mathfrak{R}$
. It does depend on
![]() $p$
and differs from the rational cluster picture when
$p$
and differs from the rational cluster picture when
![]() $p=3$
. Thus, although the cluster picture is particularly useful for Galois theoretical problems, the rational cluster picture appears to be a more suitable object for the study of regular models of the curve.
$p=3$
. Thus, although the cluster picture is particularly useful for Galois theoretical problems, the rational cluster picture appears to be a more suitable object for the study of regular models of the curve.
Finally, note that
![]() $E_p$
has an almost rational cluster picture. For any two distinct roots
$E_p$
has an almost rational cluster picture. For any two distinct roots
![]() $r,r'\in \mathfrak{R}$
, the smallest
$r,r'\in \mathfrak{R}$
, the smallest
![]() $v$
-adic disc
$v$
-adic disc
![]() $D_{r,r^{\prime}}$
containing them also contains the whole
$D_{r,r^{\prime}}$
containing them also contains the whole
![]() $\mathfrak{R}$
. The element
$\mathfrak{R}$
. The element
![]() $0\in \mathbb{Q}_p^{nr}$
belongs to
$0\in \mathbb{Q}_p^{nr}$
belongs to
![]() $D_{r,r^{\prime}}$
when
$D_{r,r^{\prime}}$
when
![]() $p\neq 3$
, while
$p\neq 3$
, while
![]() $|D_{r,r^{\prime}}\cap \mathfrak{R}|=3=|v(r)|_p$
, if
$|D_{r,r^{\prime}}\cap \mathfrak{R}|=3=|v(r)|_p$
, if
![]() $p=3$
.
$p=3$
.
The advantages of the rational cluster picture discussed in this subsection can also be observed in the following example where we study a more complex family of hyperelliptic curves having almost rational cluster picture.
1.4. Example
In this subsection we are going to present an example of a family of hyperelliptic curves
![]() $C_p$
satisfying the hypothesis of Theorems 1.7 and 1.9. Via those results we will then describe the special fibre of the minimal regular model and a basis of integral differentials of
$C_p$
satisfying the hypothesis of Theorems 1.7 and 1.9. Via those results we will then describe the special fibre of the minimal regular model and a basis of integral differentials of
![]() $C_p$
. All the computations involved are explained in detail in Examples 3.32, 4.25 and 6.5.
$C_p$
. All the computations involved are explained in detail in Examples 3.32, 4.25 and 6.5.
For any prime number
![]() $p$
, let
$p$
, let
![]() $a\in \mathbb{Z}_p$
,
$a\in \mathbb{Z}_p$
,
![]() $b\in \mathbb{Z}_p^\times$
such that the polynomial
$b\in \mathbb{Z}_p^\times$
such that the polynomial
![]() $x^2+ax+b$
is not a square modulo
$x^2+ax+b$
is not a square modulo
![]() $p$
. Let
$p$
. Let
![]() $C_p/\mathbb{Q}_p$
be the hyperelliptic curve of genus
$C_p/\mathbb{Q}_p$
be the hyperelliptic curve of genus
![]() $4$
given by
$4$
given by
![]() $y^2=f(x)$
, where
$y^2=f(x)$
, where
![]() $f(x)=(x^6+ap^4x^3+bp^8)((x-p)^3-p^{11})$
. The curve
$f(x)=(x^6+ap^4x^3+bp^8)((x-p)^3-p^{11})$
. The curve
![]() $C_p/\mathbb{Q}_p^{nr}$
has an almost rational cluster picture and is
$C_p/\mathbb{Q}_p^{nr}$
has an almost rational cluster picture and is
![]() $y$
-regular when
$y$
-regular when
![]() $p=2$
. Its rational cluster picture is
$p=2$
. Its rational cluster picture is

where
![]() $\rho _{\mathfrak{t}_3}=\frac{4}{3}$
,
$\rho _{\mathfrak{t}_3}=\frac{4}{3}$
,
![]() $\rho _{\mathfrak{t}_4}=\frac{11}{3}$
, and
$\rho _{\mathfrak{t}_4}=\frac{11}{3}$
, and
![]() $\rho _{\mathfrak{R}}=1$
. From Theorem 1.7 we can construct a regular model with strict normal crossings of
$\rho _{\mathfrak{R}}=1$
. From Theorem 1.7 we can construct a regular model with strict normal crossings of
![]() $C_p$
with special fibre
$C_p$
with special fibre

over
![]() $\bar{\mathbb{F}}_p$
. Computing the self-intersection of each irreducible component we easily see that this model coincides with the minimal regular model
$\bar{\mathbb{F}}_p$
. Computing the self-intersection of each irreducible component we easily see that this model coincides with the minimal regular model
![]() $\mathcal{C}^{\textrm{min}}$
. Theorem 4.23 also describes the action of the Galois group
$\mathcal{C}^{\textrm{min}}$
. Theorem 4.23 also describes the action of the Galois group
![]() $\textrm{Gal}(\bar{\mathbb{F}}_p/{\mathbb{F}}_p)$
on the special fibre
$\textrm{Gal}(\bar{\mathbb{F}}_p/{\mathbb{F}}_p)$
on the special fibre
![]() $\mathcal{C}_s^{\textrm{min}}$
of
$\mathcal{C}_s^{\textrm{min}}$
of
![]() $\mathcal{C}^{\textrm{min}}$
. If the roots of
$\mathcal{C}^{\textrm{min}}$
. If the roots of
![]() $x^2+ax+b\mod p$
are in
$x^2+ax+b\mod p$
are in
![]() ${\mathbb{F}}_p$
then the absolute Galois group acts trivially on each component, otherwise it swaps the
${\mathbb{F}}_p$
then the absolute Galois group acts trivially on each component, otherwise it swaps the
![]() $2$
irreducible components of multiplicity
$2$
irreducible components of multiplicity
![]() $3$
intersecting
$3$
intersecting
![]() $\Gamma _{\mathfrak{t}_3}$
.
$\Gamma _{\mathfrak{t}_3}$
.
From Theorem 1.9 it follows that, for any
![]() $p$
, a basis of integral differentials of
$p$
, a basis of integral differentials of
![]() $C_p/\mathbb{Q}_p^{nr}$
is given by
$C_p/\mathbb{Q}_p^{nr}$
is given by
In fact, this is also a basis of integral differentials of
![]() $C_p/\mathbb{Q}_p$
since they are all defined over
$C_p/\mathbb{Q}_p$
since they are all defined over
![]() $\mathbb{Q}_p$
(see Proposition B.2).
$\mathbb{Q}_p$
(see Proposition B.2).
Below we will present related works of other authors concerning regular models and integral differentials of hyperelliptic curves. Note that the example presented here is not covered by [Reference Dokchitser, Dokchitser, Maistret and Morgan14] and [Reference Dokchitser1] since the curve
![]() $C_p$
is not semistable and not
$C_p$
is not semistable and not
![]() $\Delta _v$
-regular. In fact, if
$\Delta _v$
-regular. In fact, if
![]() $p=3$
the curve
$p=3$
the curve
![]() $C_p$
does not even have tamely potential semistable reduction. The results in [Reference Faraggi and Nowell5] assume
$C_p$
does not even have tamely potential semistable reduction. The results in [Reference Faraggi and Nowell5] assume
![]() $p\gt 2$
and
$p\gt 2$
and
![]() $C_p$
with tamely potential semistable reduction, hence they cannot be used when
$C_p$
with tamely potential semistable reduction, hence they cannot be used when
![]() $p=2,3$
. Finally, there is no classification for genus
$p=2,3$
. Finally, there is no classification for genus
![]() $4$
curves.
$4$
curves.
1.5. Related works of other authors
Let
![]() $K$
be a discretely valued field with residue field
$K$
be a discretely valued field with residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
and let
$p$
and let
![]() $C/K$
be a hyperelliptic curve of genus
$C/K$
be a hyperelliptic curve of genus
![]() $g$
.
$g$
.
In genus
![]() $1$
, when
$1$
, when
![]() $k$
is perfect, thanks to Tate’s algorithm, one can describe the minimal regular model and the space of integral differentials of an elliptic curve
$k$
is perfect, thanks to Tate’s algorithm, one can describe the minimal regular model and the space of integral differentials of an elliptic curve
![]() $C$
(see e.g., [Reference Silverman24, IV.8.2], [Reference Liu9, Theorem 9.4.35]).
$C$
(see e.g., [Reference Silverman24, IV.8.2], [Reference Liu9, Theorem 9.4.35]).
If
![]() $K={\mathbb{C}}(t)$
and
$K={\mathbb{C}}(t)$
and
![]() $C$
has genus
$C$
has genus
![]() $2$
, then Namikawa and Ueno [Reference Namikawa and Ueno18] and Liu [Reference Liu12] give a full classification of the possible configurations of the special fibre of the minimal regular model of
$2$
, then Namikawa and Ueno [Reference Namikawa and Ueno18] and Liu [Reference Liu12] give a full classification of the possible configurations of the special fibre of the minimal regular model of
![]() $C$
.
$C$
.
If
![]() $p\neq 2$
, then Liu and Lorenzini show in [Reference Liu and Lorenzini13] that regular models of
$p\neq 2$
, then Liu and Lorenzini show in [Reference Liu and Lorenzini13] that regular models of
![]() $C$
can be seen as double cover of well-chosen regular models of
$C$
can be seen as double cover of well-chosen regular models of
![]() ${\mathbb{P}}^1_K$
. Since the latter can be found by using the MacLane valuations [Reference MacLane15] approach in [Reference Obus and Wewers21], this argument gives a way to describe any regular model of a hyperelliptic curve. At the moment there is no known closed form description of a regular model based on this approach and it has not been generalised to the
${\mathbb{P}}^1_K$
. Since the latter can be found by using the MacLane valuations [Reference MacLane15] approach in [Reference Obus and Wewers21], this argument gives a way to describe any regular model of a hyperelliptic curve. At the moment there is no known closed form description of a regular model based on this approach and it has not been generalised to the
![]() $p=2$
case.
$p=2$
case.
If
![]() $p\gt 2$
,
$p\gt 2$
,
![]() $k$
finite, and
$k$
finite, and
![]() $C$
is semistable, then in [Reference Dokchitser, Dokchitser, Maistret and Morgan14] the authors explicitly construct a minimal regular model in terms of the cluster picture of
$C$
is semistable, then in [Reference Dokchitser, Dokchitser, Maistret and Morgan14] the authors explicitly construct a minimal regular model in terms of the cluster picture of
![]() $C$
. Under the same assumptions, Kunzweiler [Reference Kunzweiler8] gives a basis of integral differentials rephrasing [Reference Kausz6, Proposition 5.5] in terms of the cluster invariants introduced in [Reference Dokchitser, Dokchitser, Maistret and Morgan14]. These results can be recovered from Theorem 4.23 (see Corollary 4.27) and Theorem 6.3.
$C$
. Under the same assumptions, Kunzweiler [Reference Kunzweiler8] gives a basis of integral differentials rephrasing [Reference Kausz6, Proposition 5.5] in terms of the cluster invariants introduced in [Reference Dokchitser, Dokchitser, Maistret and Morgan14]. These results can be recovered from Theorem 4.23 (see Corollary 4.27) and Theorem 6.3.
If
![]() $p\gt 2$
and
$p\gt 2$
and
![]() $C$
is semistable over some tamely ramified extension
$C$
is semistable over some tamely ramified extension
![]() $L/K$
, then Faraggi and Nowell [Reference Faraggi and Nowell5] find the special fibre of the minimal regular model of
$L/K$
, then Faraggi and Nowell [Reference Faraggi and Nowell5] find the special fibre of the minimal regular model of
![]() $C$
with strict normal crossings taking the quotient of the stable model of
$C$
with strict normal crossings taking the quotient of the stable model of
![]() $C_L$
and resolving the (tame) singularities. However, since they do not describe the charts of the model, their result does not immediately yield all arithmetic invariants, such as a basis of integral differentials.
$C_L$
and resolving the (tame) singularities. However, since they do not describe the charts of the model, their result does not immediately yield all arithmetic invariants, such as a basis of integral differentials.
The last work we want to recall represents an important ingredient of the strategy we will use in this paper (described more precisely in the next subsection). T. Dokchitser in [Reference Dokchitser1] shows that the toric resolution of
![]() $C$
gives a regular model in case of
$C$
gives a regular model in case of
![]() $\Delta _v$
-regularity [Reference Dokchitser1, Definition 3.9]. This result, used also in [Reference Faraggi and Nowell5], holds for general curves and in any residue characteristic. In his paper, Dokchitser also describes a basis of integral differentials since his model is given as open cover of affine schemes. In Corollary 3.25 and Theorem 6.1, we will rephrase his results for hyperelliptic curves by using rational cluster picture invariants from Section 3.
$\Delta _v$
-regularity [Reference Dokchitser1, Definition 3.9]. This result, used also in [Reference Faraggi and Nowell5], holds for general curves and in any residue characteristic. In his paper, Dokchitser also describes a basis of integral differentials since his model is given as open cover of affine schemes. In Corollary 3.25 and Theorem 6.1, we will rephrase his results for hyperelliptic curves by using rational cluster picture invariants from Section 3.
1.6. Strategy and outline of the paper
In [Reference Dokchitser1], Dokchitser not only describes a regular model of
![]() $C$
in case of
$C$
in case of
![]() $\Delta _v$
-regularity, but also constructs a proper flat model
$\Delta _v$
-regularity, but also constructs a proper flat model
![]() $\mathcal{C}_\Delta$
without any assumptions on
$\mathcal{C}_\Delta$
without any assumptions on
![]() $C$
. Assume
$C$
. Assume
![]() $C$
is
$C$
is
![]() $y$
-regular and has an almost rational cluster picture over
$y$
-regular and has an almost rational cluster picture over
![]() $K^{nr}$
with rational centres
$K^{nr}$
with rational centres
![]() $w_1,\dots, w_m\in K^{nr}$
. Our approach to construct the minimal regular model with normal crossings of
$w_1,\dots, w_m\in K^{nr}$
. Our approach to construct the minimal regular model with normal crossings of
![]() $C$
is composed by the following steps:
$C$
is composed by the following steps:
-
Consider the
 $x$
-translated hyperelliptic curves
$x$
-translated hyperelliptic curves
 $C^{w_h}/K^{nr}:y^2=f(x+w_h)$
, for
$C^{w_h}/K^{nr}:y^2=f(x+w_h)$
, for
 $h=1,\dots,m$
. For each
$h=1,\dots,m$
. For each
 $h$
, [Reference Dokchitser1, Theorem 3.14] constructs a proper flat model
$h$
, [Reference Dokchitser1, Theorem 3.14] constructs a proper flat model
 $\mathcal{C}_\Delta ^{w_h}$
, possibly singular.
$\mathcal{C}_\Delta ^{w_h}$
, possibly singular. -
We glue regular open subschemes of these models along common opens, and show that the result is a proper flat regular model
 $\mathcal{C}$
of
$\mathcal{C}$
of
 $C_{K^{nr}}$
with strict normal crossings.
$C_{K^{nr}}$
with strict normal crossings. -
We give a complete description of what components of the special fibre of
 $\mathcal{C}$
have to be blown down to obtain the minimal model with normal crossings
$\mathcal{C}$
have to be blown down to obtain the minimal model with normal crossings
 $\mathcal{C}^{\textrm{min}}$
of
$\mathcal{C}^{\textrm{min}}$
of
 $C_{K^{nr}}$
.
$C_{K^{nr}}$
. -
Finally, we describe the action of the absolute Galois group
 $G_k$
of
$G_k$
of
 $k$
on the special fibre of
$k$
on the special fibre of
 $\mathcal{C}^{\textrm{min}}$
.
$\mathcal{C}^{\textrm{min}}$
.
We will explicitly describe both the models
![]() $\mathcal{C}_\Delta ^{w_h}$
and
$\mathcal{C}_\Delta ^{w_h}$
and
![]() $\mathcal{C}$
. This allows us to study the global sections of its relative dualising sheaf
$\mathcal{C}$
. This allows us to study the global sections of its relative dualising sheaf
![]() $\omega _{\mathcal{C}/O_K}(\mathcal{C})$
.
$\omega _{\mathcal{C}/O_K}(\mathcal{C})$
.
In Section 2, we present some results on Newton polygons used in the following sections. In Section 3, we recall the basic objects and notation of [Reference Dokchitser, Dokchitser, Maistret and Morgan14] and define the rational cluster picture. Moreover, we relate it with the notions given in Section 2. This comparison allows us to rephrase the objects in [Reference Dokchitser1] in terms of rational clusters invariants in Section 4. In the same section we also state the theorems which describe the special fibres of a proper flat model (Theorem 4.18) and of the minimal regular model with normal crossings (Theorem 4.23) of
![]() $C$
. The construction of these models, from which the two theorems above follow, is presented in Section 5. Finally, in Section 6, Theorems 6.3 and 6.4 describe a basis of integral differentials of
$C$
. The construction of these models, from which the two theorems above follow, is presented in Section 5. Finally, in Section 6, Theorems 6.3 and 6.4 describe a basis of integral differentials of
![]() $C$
, in terms of rational clusters invariants defined in Section 3.
$C$
, in terms of rational clusters invariants defined in Section 3.
1.7. Notation
In the following, we present the main notation used for fields, hyperelliptic curves and Newton polytopes.
|
|
complete field with normalised discrete valuation
|
|
|
ring of integers, uniformiser, residue field,
|
|
|
fixed algebraic closure of
|
|
|
separable closure, maximal unramified extension of
|
|
|
ring of integers of
|
|
|
extension of
|
|
|
absolute Galois groups
|
|
|
|
|
|
Newton polygon of
|
|
|
restriction and reduction of
|
|
|
|
|
|
hyperelliptic curve defined over
|
|
|
|
|
|
|
|
|
|
|
|
Newton polytopes attached to
|
|
|
|
|
|
|
For a separable polynomial
![]() $f\in k[x]$
or a hyperelliptic curve
$f\in k[x]$
or a hyperelliptic curve
![]() $C/K:y^2=f(x)$
as above, the following is the main notation for clusters.
$C/K:y^2=f(x)$
as above, the following is the main notation for clusters.
|
|
leading coefficient and set of roots of
|
|
|
cluster picture, the set of clusters of
|
|
|
cluster,
|
|
|
|
|
|
|
|
|
|
|
|
smallest cluster containing
|
|
|
|
|
|
denominator of
|
|
|
rational centre of
|
|
|
|
|
|
rational cluster picture (Definition 3.9) |
|
|
rational cluster (Definition 3.9) |
|
|
|
|
|
cluster picture centred at
|
|
|
cluster centred at
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
polynomials in one variable over
|
In Section 5 we explicitly construct proper flat models of hyperelliptic curves and study the conditions for having (minimal) regular models with normal crossings. Here you can find the most used objects and notation.
|
|
|
|
|
a rationally minimal cluster, element of
|
|
|
|
|
|
fixed rational centre of
|
|
|
|
|
|
|
|
|
matrix associated to a proper rational cluster
|
|
|
change of variable
|
|
|
integer, cone, toric scheme attached to a matrix
|
|
|
entries of the matrices
|
|
|
|
|
|
proper model of
|
|
|
closure of
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sets attached to a rational cluster
|
|
|
|
|
|
|
|
|
|
2. Newton polygon
Let
![]() $K$
be a complete field with a normalised valuation
$K$
be a complete field with a normalised valuation
![]() $v$
, ring of integers
$v$
, ring of integers
![]() $O_K$
, uniformiser
$O_K$
, uniformiser
![]() $\pi$
, and residue field
$\pi$
, and residue field
![]() $ k$
of characteristic
$ k$
of characteristic
![]() $p$
. We fix
$p$
. We fix
![]() $\bar{K}$
, an algebraic closure of
$\bar{K}$
, an algebraic closure of
![]() $K$
, of residue field
$K$
, of residue field
![]() $\bar{k}$
, and we denote by
$\bar{k}$
, and we denote by
![]() $K^{\textrm{s}}$
the separable closure of
$K^{\textrm{s}}$
the separable closure of
![]() $K$
in
$K$
in
![]() $\bar{K}$
. Denote by
$\bar{K}$
. Denote by
![]() $K^{nr}$
the maximal unramified extension of
$K^{nr}$
the maximal unramified extension of
![]() $K$
in
$K$
in
![]() $K^{\textrm{s}}$
, by
$K^{\textrm{s}}$
, by
![]() $O_{K^{nr}}$
its ring of integers, and by
$O_{K^{nr}}$
its ring of integers, and by
![]() $ k^{\textrm{s}}$
its residue field. Note that
$ k^{\textrm{s}}$
its residue field. Note that
![]() $ k^{\textrm{s}}$
is the separable closure of
$ k^{\textrm{s}}$
is the separable closure of
![]() $k$
in
$k$
in
![]() $\bar{k}$
. Extend the valuation
$\bar{k}$
. Extend the valuation
![]() $v$
to
$v$
to
![]() $\bar{K}$
. Finally, write
$\bar{K}$
. Finally, write
![]() $G_K$
,
$G_K$
,
![]() $G_k$
for the Galois groups
$G_k$
for the Galois groups
![]() $\textrm{Gal}(K^{\textrm{s}}/K)$
,
$\textrm{Gal}(K^{\textrm{s}}/K)$
,
![]() $\textrm{Gal}( k^{\textrm{s}}/ k)$
, respectively.
$\textrm{Gal}( k^{\textrm{s}}/ k)$
, respectively.
Notation 2.1.
Let
![]() $O_{\bar{K}}=\{a\in \bar{K}\mid v(a)\geq 0\}$
. Throughout this paper, given an element
$O_{\bar{K}}=\{a\in \bar{K}\mid v(a)\geq 0\}$
. Throughout this paper, given an element
![]() $a\in O_{\bar{K}}$
, we will write
$a\in O_{\bar{K}}$
, we will write
![]() $a\mod \pi$
for the reduction of
$a\mod \pi$
for the reduction of
![]() $a$
in
$a$
in
![]() $\bar{k}$
. Similarly, given a polynomial
$\bar{k}$
. Similarly, given a polynomial
![]() $h\in O_{\bar{K}}[x_1,\dots,x_n]$
, namely
$h\in O_{\bar{K}}[x_1,\dots,x_n]$
, namely
![]() $h=\sum a_{i_1,\dots,i_n}\cdot x_1^{i_1}\cdots x_n^{i_n}$
, we will write
$h=\sum a_{i_1,\dots,i_n}\cdot x_1^{i_1}\cdots x_n^{i_n}$
, we will write
![]() $h\mod \pi$
for the polynomial
$h\mod \pi$
for the polynomial
![]() $\sum (a_{i_1,\dots,i_n}\mod \pi )\cdot x_1^{i_1}\cdots x_n^{i_n}\in \bar{k}[x_1,\dots,x_n]$
.
$\sum (a_{i_1,\dots,i_n}\mod \pi )\cdot x_1^{i_1}\cdots x_n^{i_n}\in \bar{k}[x_1,\dots,x_n]$
.
Let
![]() $f\in K[x]$
be a non-zero polynomial of degree
$f\in K[x]$
be a non-zero polynomial of degree
![]() $d$
, say
$d$
, say
The Newton polygon of
![]() $f$
, denoted
$f$
, denoted
![]() $\texttt{NP}(f)$
, is
$\texttt{NP}(f)$
, is
We recall the following well-known result (see e.g., [Reference Neukirch17, II.6.3,6.4]).
Theorem 2.2.
Let
![]() $i_0\lt \ldots \lt i_s=d$
be the set of indices in
$i_0\lt \ldots \lt i_s=d$
be the set of indices in
![]() $\{0,\dots,d\}$
such that the points
$\{0,\dots,d\}$
such that the points
![]() $(i_0,v(a_{i_0})),\dots,(i_s,v(a_{i_s}))$
are the vertices of
$(i_0,v(a_{i_0})),\dots,(i_s,v(a_{i_s}))$
are the vertices of
![]() $\texttt{NP}(f)$
. For any
$\texttt{NP}(f)$
. For any
![]() $j=1,\dots,s$
, denote by
$j=1,\dots,s$
, denote by
![]() $\rho _j$
the slope of the edge of
$\rho _j$
the slope of the edge of
![]() $\texttt{NP}(f)$
which links the points
$\texttt{NP}(f)$
which links the points
![]() $(i_{j-1},v(a_{i_{j-1}}))$
and
$(i_{j-1},v(a_{i_{j-1}}))$
and
![]() $(i_j,v(a_{i_j}))$
. Then
$(i_j,v(a_{i_j}))$
. Then
![]() $f$
has a unique factorisation over
$f$
has a unique factorisation over
![]() $K$
as a product
$K$
as a product
where
![]() $g_0=x^{i_0}$
and, for all
$g_0=x^{i_0}$
and, for all
![]() $j=1,\dots, s$
,
$j=1,\dots, s$
,
-
the polynomials
 $g_j\in K[x]$
are monic of degree
$g_j\in K[x]$
are monic of degree
 $d_j=i_j-i_{j-1}$
,
$d_j=i_j-i_{j-1}$
, -
all the roots of
 $g_j$
have valuation
$g_j$
have valuation
 $-\rho _j$
in
$-\rho _j$
in
 $\bar{K}$
.
$\bar{K}$
.
In particular,
![]() $\texttt{NP}(g_j)$
is a segment of slope
$\texttt{NP}(g_j)$
is a segment of slope
![]() $\rho _j$
.
$\rho _j$
.
Corollary 2.3.
With the notation of Theorem 2.2, the polynomial
![]() $f$
has exactly
$f$
has exactly
![]() $d_j$
roots of valuation
$d_j$
roots of valuation
![]() $-\rho _j$
for all
$-\rho _j$
for all
![]() $j=1,\dots,s$
.
$j=1,\dots,s$
.
Corollary 2.4.
If
![]() $f=\sum a_ix^i$
is irreducible of degree
$f=\sum a_ix^i$
is irreducible of degree
![]() $d$
and
$d$
and
![]() $a_0\neq 0$
, then
$a_0\neq 0$
, then
![]() $\texttt{NP}(f)$
is a segment linking the points
$\texttt{NP}(f)$
is a segment linking the points
![]() $(0,v(a_0))$
and
$(0,v(a_0))$
and
![]() $(d,v(a_d))$
.
$(d,v(a_d))$
.
Definition 2.5 (Restriction and reduction). Let
![]() $f=\sum _{i=0}^da_ix^i\in K[x]$
and consider an edge
$f=\sum _{i=0}^da_ix^i\in K[x]$
and consider an edge
![]() $L$
of its Newton polygon
$L$
of its Newton polygon
![]() $\texttt{NP}(f)$
. Let
$\texttt{NP}(f)$
. Let
![]() $(i_1,v(a_{i_1})), (i_2,v(a_{i_2}))$
,
$(i_1,v(a_{i_1})), (i_2,v(a_{i_2}))$
,
![]() $i_1\lt i_2$
be the two endpoints of
$i_1\lt i_2$
be the two endpoints of
![]() $L$
. Denote by
$L$
. Denote by
![]() $\rho$
the slope of
$\rho$
the slope of
![]() $L$
and by
$L$
and by
![]() $n$
the denominator of
$n$
the denominator of
![]() $\rho$
. Define the restriction of
$\rho$
. Define the restriction of
![]() $f$
to
$f$
to
![]() $L$
as
$L$
as
Moreover, we define the reduction of
![]() $f$
with respect to
$f$
with respect to
![]() $L$
to be the polynomial
$L$
to be the polynomial
where
![]() $c=v(a_{i_1})=v(a_{i_2})+(i_1-i_2)\rho .$
$c=v(a_{i_1})=v(a_{i_2})+(i_1-i_2)\rho .$
Remark 2.6.
These definitions coincide with the ones given in [
Reference Dokchitser1, Definitions 3.4, 3.5] when the number of variables is
![]() $1$
(for suitable choices of basis of the lattices used in the definitions).
$1$
(for suitable choices of basis of the lattices used in the definitions).
Until the end of the section let
![]() $f\in K[x]$
, consider a factorisation
$f\in K[x]$
, consider a factorisation
![]() $f=a_d\cdot g_0\cdot g_1\cdots g_s$
as in Theorem 2.2. Denote by
$f=a_d\cdot g_0\cdot g_1\cdots g_s$
as in Theorem 2.2. Denote by
![]() $L_j$
the edge of slope
$L_j$
the edge of slope
![]() $\rho _j$
of
$\rho _j$
of
![]() $\texttt{NP}(f)$
, for any
$\texttt{NP}(f)$
, for any
![]() $j=1\dots s$
.
$j=1\dots s$
.
Remark 2.7.
By the lower convexity of
![]() $\texttt{NP}(f)$
, for all
$\texttt{NP}(f)$
, for all
![]() $j=1,\dots,s$
, note that
$j=1,\dots,s$
, note that
![]() ${\overline{f|_{L_j}}}=\bar{c}_j\cdot{\overline{g_j|_{\texttt{NP}(g_j)}}}$
for some
${\overline{f|_{L_j}}}=\bar{c}_j\cdot{\overline{g_j|_{\texttt{NP}(g_j)}}}$
for some
![]() $\bar{c}_j\in k^\times$
. In particular they define the same
$\bar{c}_j\in k^\times$
. In particular they define the same
![]() $ k$
-scheme in
$ k$
-scheme in
![]() $\mathbb{G}_{m, k}$
. More precisely, for any
$\mathbb{G}_{m, k}$
. More precisely, for any
![]() $j=1,\dots,s$
, let
$j=1,\dots,s$
, let
Then
![]() $\bar{c}_j=u_j/\pi ^{v(u_j)}\mod \pi$
.
$\bar{c}_j=u_j/\pi ^{v(u_j)}\mod \pi$
.
Definition 2.8.
We say that
![]() $f$
is
$f$
is
![]() $\texttt{NP}$
-regular if the
$\texttt{NP}$
-regular if the
![]() $ k$
-scheme
$ k$
-scheme
is smooth for all
![]() $j=1,\dots,s$
.
$j=1,\dots,s$
.
Lemma 2.9.
The polynomial
![]() $f=a_d\cdot g_0\cdot g_1\cdots g_s$
is
$f=a_d\cdot g_0\cdot g_1\cdots g_s$
is
![]() $\texttt{NP}$
-regular if and only if
$\texttt{NP}$
-regular if and only if
![]() $g_j$
is
$g_j$
is
![]() $\texttt{NP}$
-regular for every
$\texttt{NP}$
-regular for every
![]() $j=1,\dots,s$
.
$j=1,\dots,s$
.
Proof. The Lemma follows from Remark 2.7.
We conclude this section with two examples.
Example 2.10.
Let
![]() $f=x^{11}+9x^7-3x^6+9x^5+81x-27\in \mathbb{Q}_3[x]$
. Then the Newton polygon of
$f=x^{11}+9x^7-3x^6+9x^5+81x-27\in \mathbb{Q}_3[x]$
. Then the Newton polygon of
![]() $f$
is
$f$
is

Corollary 2.3 implies that
![]() $f$
has
$f$
has
![]() $6$
roots of valuation
$6$
roots of valuation
![]() $\frac{1}{3}$
and
$\frac{1}{3}$
and
![]() $5$
roots of valuation
$5$
roots of valuation
![]() $\frac{1}{5}$
. Furthermore, the two polynomials
$\frac{1}{5}$
. Furthermore, the two polynomials
![]() $g_1$
and
$g_1$
and
![]() $g_2$
in the factorisation
$g_2$
in the factorisation
![]() $f=g_1\cdot g_2$
of Theorem 2.2 turn out to be
$f=g_1\cdot g_2$
of Theorem 2.2 turn out to be
Finally,
and
Thus
![]() $f$
is
$f$
is
![]() $\texttt{NP}$
-regular.
$\texttt{NP}$
-regular.
Example 2.11.
We now show an example of a polynomial that is not
![]() $\texttt{NP}$
-regular. Let
$\texttt{NP}$
-regular. Let
![]() $f=x^9+12x^6+36x^3+81\in \mathbb{Q}_3[x]$
. Then the Newton polygon of
$f=x^9+12x^6+36x^3+81\in \mathbb{Q}_3[x]$
. Then the Newton polygon of
![]() $f$
is
$f$
is

Corollary 2.3 implies that
![]() $f$
has
$f$
has
![]() $3$
roots of valuation
$3$
roots of valuation
![]() $\frac{2}{3}$
and
$\frac{2}{3}$
and
![]() $6$
roots of valuation
$6$
roots of valuation
![]() $\frac{1}{3}$
. Furthermore, the two polynomials
$\frac{1}{3}$
. Furthermore, the two polynomials
![]() $g_1$
and
$g_1$
and
![]() $g_2$
in the factorisation
$g_2$
in the factorisation
![]() $f=g_1\cdot g_2$
of Theorem 2.2 are
$f=g_1\cdot g_2$
of Theorem 2.2 are
Finally,
and
Then
![]() $f$
is not
$f$
is not
![]() $\texttt{NP}$
-regular. In fact, in accordance with Lemma 2.9,
$\texttt{NP}$
-regular. In fact, in accordance with Lemma 2.9,
![]() $g_2$
is not
$g_2$
is not
![]() $\texttt{NP}$
-regular.
$\texttt{NP}$
-regular.
3. Rational clusters
In this subsection we introduce simple combinatorial objects, that we call rational clusters, attached to a separable polynomial
![]() $f\in K[x]$
. Via this new terminology, we will give a characterisation for the
$f\in K[x]$
. Via this new terminology, we will give a characterisation for the
![]() $\texttt{NP}$
-regularity, from which the definition of almost rational cluster picture, key condition for the next sections, will follow. In fact, rational clusters are the main objects we will use for the construction of models and the description of integral differentials of hyperelliptic curves in Sections 5 and 6.
$\texttt{NP}$
-regularity, from which the definition of almost rational cluster picture, key condition for the next sections, will follow. In fact, rational clusters are the main objects we will use for the construction of models and the description of integral differentials of hyperelliptic curves in Sections 5 and 6.
From now on, let
![]() $f\in K[x]$
be a separable polynomial and denote by
$f\in K[x]$
be a separable polynomial and denote by
![]() $\mathfrak{R}$
the set of its roots in
$\mathfrak{R}$
the set of its roots in
![]() $K^{\textrm{s}}$
and by
$K^{\textrm{s}}$
and by
![]() $c_f$
its leading coefficient. Then
$c_f$
its leading coefficient. Then
Definition 3.1 ([Reference Dokchitser, Dokchitser, Maistret and Morgan14, Definition 1.1]). A cluster (for
![]() $f$
) is a non-empty subset
$f$
) is a non-empty subset
![]() $\mathfrak{s}\subseteq \mathfrak{R}$
of the form
$\mathfrak{s}\subseteq \mathfrak{R}$
of the form
![]() $\mathcal{D}\cap \mathfrak{R}$
, where
$\mathcal{D}\cap \mathfrak{R}$
, where
![]() $\mathcal{D}$
is a
$\mathcal{D}$
is a
![]() $v$
-adic disc
$v$
-adic disc
![]() $\mathcal{D}=\{x\in \bar{K}\mid v(x-z)\geq d\}$
for some
$\mathcal{D}=\{x\in \bar{K}\mid v(x-z)\geq d\}$
for some
![]() $z\in \bar{K}$
and
$z\in \bar{K}$
and
![]() $d\in \mathbb{Q}$
. If
$d\in \mathbb{Q}$
. If
![]() $|\mathfrak{s}|\gt 1$
we say that
$|\mathfrak{s}|\gt 1$
we say that
![]() $\mathfrak{s}$
is proper and define its depth
$\mathfrak{s}$
is proper and define its depth
![]() $d_{\mathfrak{s}}$
to be
$d_{\mathfrak{s}}$
to be
Note that every proper cluster is cut out by a disc of the form
for any
![]() $r\in \mathfrak{s}$
.
$r\in \mathfrak{s}$
.
Definition 3.2 ([Reference Dokchitser, Dokchitser, Maistret and Morgan14, Definition 1.26]). The cluster picture of
![]() $f$
is the collection of its clusters, together with their depths.
$f$
is the collection of its clusters, together with their depths.
We denote by
![]() $\Sigma _f$
the set of all clusters of
$\Sigma _f$
the set of all clusters of
![]() $f$
and by
$f$
and by
![]() $\mathring{\Sigma }_f$
the subset of
$\mathring{\Sigma }_f$
the subset of
![]() $\Sigma _f$
of proper clusters.
$\Sigma _f$
of proper clusters.
Definition 3.3 ([Reference Dokchitser, Dokchitser, Maistret and Morgan14, Definition 1.3]). If
![]() $\mathfrak{s}^{\prime}\subsetneq \mathfrak{s}$
is maximal subcluster, then we say that
$\mathfrak{s}^{\prime}\subsetneq \mathfrak{s}$
is maximal subcluster, then we say that
![]() $\mathfrak{s}^{\prime}$
is a child of
$\mathfrak{s}^{\prime}$
is a child of
![]() $\mathfrak{s}$
and
$\mathfrak{s}$
and
![]() $\mathfrak{s}$
is the parent of
$\mathfrak{s}$
is the parent of
![]() $\mathfrak{s}^{\prime}$
, and we write
$\mathfrak{s}^{\prime}$
, and we write
![]() $\mathfrak{s}^{\prime}\lt \mathfrak{s}$
. For any
$\mathfrak{s}^{\prime}\lt \mathfrak{s}$
. For any
![]() $\mathfrak{s}^{\prime},\mathfrak{s}\in \Sigma _f$
, we write
$\mathfrak{s}^{\prime},\mathfrak{s}\in \Sigma _f$
, we write
![]() $\mathfrak{s}^{\prime}\leq \mathfrak{s}$
if either
$\mathfrak{s}^{\prime}\leq \mathfrak{s}$
if either
![]() $\mathfrak{s}^{\prime}\lt \mathfrak{s}$
or
$\mathfrak{s}^{\prime}\lt \mathfrak{s}$
or
![]() $\mathfrak{s}^{\prime}=\mathfrak{s}$
. Since every cluster
$\mathfrak{s}^{\prime}=\mathfrak{s}$
. Since every cluster
![]() $\mathfrak{s}\neq \mathfrak{R}$
has one and only one parent we write
$\mathfrak{s}\neq \mathfrak{R}$
has one and only one parent we write
![]() $P(\mathfrak{s})$
to refer to the unique parent of
$P(\mathfrak{s})$
to refer to the unique parent of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
We say that a proper cluster
![]() $\mathfrak{s}$
is minimal if it does not have any proper child.
$\mathfrak{s}$
is minimal if it does not have any proper child.
For two clusters (or roots)
![]() ${\mathfrak{s}}_1,{\mathfrak{s}}_2$
, we write
${\mathfrak{s}}_1,{\mathfrak{s}}_2$
, we write
![]() ${\mathfrak{s}}_1\wedge{\mathfrak{s}}_2$
for the smallest cluster that contains them.
${\mathfrak{s}}_1\wedge{\mathfrak{s}}_2$
for the smallest cluster that contains them.
Definition 3.4 ([Reference Dokchitser, Dokchitser, Maistret and Morgan14, Definition 1.4]). A cluster
![]() $\mathfrak{s}$
is odd/even if its size is odd/even. If
$\mathfrak{s}$
is odd/even if its size is odd/even. If
![]() $|\mathfrak{s}|=2$
, then we say
$|\mathfrak{s}|=2$
, then we say
![]() $\mathfrak{s}$
is a twin. A cluster
$\mathfrak{s}$
is a twin. A cluster
![]() $\mathfrak{s}$
is übereven if it has only even children.
$\mathfrak{s}$
is übereven if it has only even children.
Definition 3.5 ([Reference Dokchitser, Dokchitser, Maistret and Morgan14, Definition 1.9]). A centre
![]() $z_{\mathfrak{s}}$
of a proper cluster
$z_{\mathfrak{s}}$
of a proper cluster
![]() $\mathfrak{s}$
is any element
$\mathfrak{s}$
is any element
![]() $z_{\mathfrak{s}}\in K^{\textrm{s}}$
such that
$z_{\mathfrak{s}}\in K^{\textrm{s}}$
such that
![]() $\mathfrak{s}=\mathcal{D}\cap \mathfrak{R}$
, where
$\mathfrak{s}=\mathcal{D}\cap \mathfrak{R}$
, where
Equivalently,
![]() $v(r-z_{\mathfrak{s}})\geq d_{\mathfrak{s}}$
for all
$v(r-z_{\mathfrak{s}})\geq d_{\mathfrak{s}}$
for all
![]() $r\in \mathfrak{s}$
. The centre of a non-proper cluster
$r\in \mathfrak{s}$
. The centre of a non-proper cluster
![]() $\mathfrak{s}=\{r\}$
is
$\mathfrak{s}=\{r\}$
is
![]() $r$
.
$r$
.
Definition 3.6 ([Reference Dokchitser, Dokchitser, Maistret and Morgan14, Definition 1.6]). For a proper cluster
![]() $\mathfrak{s}$
set
$\mathfrak{s}$
set
Definition 3.7.
We say that
![]() $\Sigma _f$
is nested if one of the following equivalent conditions is satisfied:
$\Sigma _f$
is nested if one of the following equivalent conditions is satisfied:
-
(i) there exists
 $z\in K^{\textrm{s}}$
such that
$z\in K^{\textrm{s}}$
such that
 $z$
is a centre for all proper clusters
$z$
is a centre for all proper clusters
 $\mathfrak{s}\in \Sigma _f$
;
$\mathfrak{s}\in \Sigma _f$
; -
(ii) there is only one minimal cluster in
 $\Sigma _f$
;
$\Sigma _f$
; -
(iii) every non-minimal proper cluster has exactly one proper child.
Definition 3.8.
A rational centre of a cluster
![]() $\mathfrak{s}$
is any element
$\mathfrak{s}$
is any element
![]() $w_{\mathfrak{s}}\in K$
such that
$w_{\mathfrak{s}}\in K$
such that
If
![]() $\mathfrak{s}=\{r\}$
, with
$\mathfrak{s}=\{r\}$
, with
![]() $r\in K$
, then
$r\in K$
, then
![]() $w_{\mathfrak{s}}=r$
.
$w_{\mathfrak{s}}=r$
.
If
![]() $w_{\mathfrak{s}}$
is a rational centre of a proper cluster
$w_{\mathfrak{s}}$
is a rational centre of a proper cluster
![]() $\mathfrak{s}$
, we define the radius of
$\mathfrak{s}$
, we define the radius of
![]() $\mathfrak{s}$
to be
$\mathfrak{s}$
to be
Definition 3.9.
A rational cluster is a cluster cut out by a
![]() $v$
-adic disc of the form
$v$
-adic disc of the form
![]() $\mathcal{D}=\{x\in \bar{K}\mid v(x-w)\geq d\}$
with
$\mathcal{D}=\{x\in \bar{K}\mid v(x-w)\geq d\}$
with
![]() $w\in K$
and
$w\in K$
and
![]() $d\in \mathbb{Q}$
.
$d\in \mathbb{Q}$
.
The rational cluster picture is the collection of all rational clusters of
![]() $f$
together with their radii.
$f$
together with their radii.
We denote by
![]() $\Sigma _f^{\textrm{rat}}\subseteq \Sigma _f$
the set of rational clusters and by
$\Sigma _f^{\textrm{rat}}\subseteq \Sigma _f$
the set of rational clusters and by
![]() $\mathring{\Sigma }_f^{\textrm{rat}}$
the subset of
$\mathring{\Sigma }_f^{\textrm{rat}}$
the subset of
![]() $\Sigma _f^{\textrm{rat}}$
of proper rational clusters.
$\Sigma _f^{\textrm{rat}}$
of proper rational clusters.
Lemma 3.10.
Let
![]() $\mathfrak{s}$
be a proper cluster. Then
$\mathfrak{s}$
be a proper cluster. Then
![]() $d_{\mathfrak{s}}\geq \rho _{\mathfrak{s}}$
.
$d_{\mathfrak{s}}\geq \rho _{\mathfrak{s}}$
.
Proof. First we want to show that
Clearly
![]() $\min _{r,r^{\prime}\in \mathfrak{s}}v(r-r')\leq \max _{z\in K^{\textrm{s}}}\min _{r\in \mathfrak{s}}v(r-z)$
. Let
$\min _{r,r^{\prime}\in \mathfrak{s}}v(r-r')\leq \max _{z\in K^{\textrm{s}}}\min _{r\in \mathfrak{s}}v(r-z)$
. Let
![]() $z_{\mathfrak{s}}\in K^{\textrm{s}}$
such that
$z_{\mathfrak{s}}\in K^{\textrm{s}}$
such that
Then, for any
![]() $r,r'\in \mathfrak{s}$
, one has
$r,r'\in \mathfrak{s}$
, one has
and so
as required. From
the Lemma follows.
Thanks to the previous lemma, the next definition gives, for any cluster
![]() $\mathfrak{s}$
, the smallest rational cluster containing it.
$\mathfrak{s}$
, the smallest rational cluster containing it.
Definition 3.11.
Given a proper cluster
![]() $\mathfrak{s}\in \Sigma _f$
, we define the rationalisation
$\mathfrak{s}\in \Sigma _f$
, we define the rationalisation
![]() ${\mathfrak{s}}^{\textrm{rat}}$
of
${\mathfrak{s}}^{\textrm{rat}}$
of
![]() $\mathfrak{s}$
to be the smallest rational cluster containing
$\mathfrak{s}$
to be the smallest rational cluster containing
![]() $\mathfrak{s}$
. By definition
$\mathfrak{s}$
. By definition
where
![]() $w_{\mathfrak{s}}$
is a rational centre of
$w_{\mathfrak{s}}$
is a rational centre of
![]() $\mathfrak{s}$
and
$\mathfrak{s}$
and
![]() $\rho _{\mathfrak{s}}$
is its radius.
$\rho _{\mathfrak{s}}$
is its radius.
The next Lemma will be used in Section 5 to prove the minimality of the regular model with normal crossings we construct.
Lemma 3.12.
Let
![]() $\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
be a proper cluster with rational centre
$\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
be a proper cluster with rational centre
![]() $w_{\mathfrak{s}}$
. Let
$w_{\mathfrak{s}}$
. Let
![]() $\mathfrak{s}^{\prime}\in \Sigma _C^{\textrm{rat}}$
be the child of
$\mathfrak{s}^{\prime}\in \Sigma _C^{\textrm{rat}}$
be the child of
![]() $\mathfrak{s}$
with rational centre
$\mathfrak{s}$
with rational centre
![]() $w_{\mathfrak{s}}$
(let
$w_{\mathfrak{s}}$
(let
![]() $\mathfrak{s}^{\prime}=\varnothing$
if it does not exist). Then
$\mathfrak{s}^{\prime}=\varnothing$
if it does not exist). Then
![]() $(|\mathfrak{s}|-|\mathfrak{s}^{\prime}|)\rho _{\mathfrak{s}}\in \mathbb{Z}$
.
$(|\mathfrak{s}|-|\mathfrak{s}^{\prime}|)\rho _{\mathfrak{s}}\in \mathbb{Z}$
.
Proof. As
![]() $\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
, one has
$\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
, one has
![]() $\mathfrak{s}={\mathfrak{s}}^{\textrm{rat}}$
. Let
$\mathfrak{s}={\mathfrak{s}}^{\textrm{rat}}$
. Let
![]() $b_{\mathfrak{s}}$
be the denominator of
$b_{\mathfrak{s}}$
be the denominator of
![]() $\rho _{\mathfrak{s}}$
. Then
$\rho _{\mathfrak{s}}$
. Then
![]() $b_{\mathfrak{s}}$
divides the degree of the minimal polynomial of
$b_{\mathfrak{s}}$
divides the degree of the minimal polynomial of
![]() $r$
, for any
$r$
, for any
![]() $r\in \mathfrak{s}$
satisfying
$r\in \mathfrak{s}$
satisfying
![]() $v(w_{\mathfrak{s}}-r)=\rho _{\mathfrak{s}}$
. Then
$v(w_{\mathfrak{s}}-r)=\rho _{\mathfrak{s}}$
. Then
![]() $(|\mathfrak{s}|-|\mathfrak{s}^{\prime}|)\rho _{\mathfrak{s}}\in \mathbb{Z}$
, where
$(|\mathfrak{s}|-|\mathfrak{s}^{\prime}|)\rho _{\mathfrak{s}}\in \mathbb{Z}$
, where
as required.
By definition, a rational cluster is
![]() $G_K$
-invariant. Apart from that necessary condition, it is not easy to see whether a proper cluster
$G_K$
-invariant. Apart from that necessary condition, it is not easy to see whether a proper cluster
![]() $\mathfrak{s}$
is also a rational cluster in general. The following remark gives a sufficient condition and shows we have a simple characterisation when
$\mathfrak{s}$
is also a rational cluster in general. The following remark gives a sufficient condition and shows we have a simple characterisation when
![]() $K(\mathfrak{s})/K$
is tamely ramified.
$K(\mathfrak{s})/K$
is tamely ramified.
Remark 3.13.
If a proper cluster
![]() $\mathfrak{s}\in \Sigma _f$
satisfies
$\mathfrak{s}\in \Sigma _f$
satisfies
![]() $d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
, then a rational centre
$d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
, then a rational centre
![]() $w_{\mathfrak{s}}\in K$
of its is also a centre. Hence
$w_{\mathfrak{s}}\in K$
of its is also a centre. Hence
![]() $\mathfrak{s}$
is a rational cluster and, in particular, is
$\mathfrak{s}$
is a rational cluster and, in particular, is
![]() $G_K$
-invariant. On the other hand, if a proper cluster
$G_K$
-invariant. On the other hand, if a proper cluster
![]() $\mathfrak{s}\in \Sigma _f$
is
$\mathfrak{s}\in \Sigma _f$
is
![]() $G_K$
-invariant and
$G_K$
-invariant and
![]() $K(\mathfrak{s})/K$
is tamely ramified, then
$K(\mathfrak{s})/K$
is tamely ramified, then
![]() $\mathfrak{s}$
has a centre
$\mathfrak{s}$
has a centre
![]() $z_{\mathfrak{s}}\in K$
by [Reference Dokchitser, Dokchitser, Maistret and Morgan14
, Lemma B.1]. Thus
$z_{\mathfrak{s}}\in K$
by [Reference Dokchitser, Dokchitser, Maistret and Morgan14
, Lemma B.1]. Thus
![]() $\rho _{\mathfrak{s}}=d_{\mathfrak{s}}$
and
$\rho _{\mathfrak{s}}=d_{\mathfrak{s}}$
and
![]() $\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
.
$\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
.
Lemma 3.14.
Let
![]() $\mathfrak{s}$
be a proper cluster with rational centre
$\mathfrak{s}$
be a proper cluster with rational centre
![]() $w_{\mathfrak{s}}$
and let
$w_{\mathfrak{s}}$
and let
![]() $\mathfrak{t}\in \Sigma _f$
satisfying
$\mathfrak{t}\in \Sigma _f$
satisfying
![]() $\mathfrak{t}\supseteq \mathfrak{s}$
. Then
$\mathfrak{t}\supseteq \mathfrak{s}$
. Then
![]() $w_{\mathfrak{s}}$
is a rational centre of
$w_{\mathfrak{s}}$
is a rational centre of
![]() $\mathfrak{t}$
and
$\mathfrak{t}$
and
![]() $\rho _{\mathfrak{t}}\leq \rho _{\mathfrak{s}}$
. Furthermore, if
$\rho _{\mathfrak{t}}\leq \rho _{\mathfrak{s}}$
. Furthermore, if
![]() $\mathfrak{s}$
is a rational cluster and
$\mathfrak{s}$
is a rational cluster and
![]() $\mathfrak{t}\supsetneq \mathfrak{s}$
, then
$\mathfrak{t}\supsetneq \mathfrak{s}$
, then
![]() $\rho _{\mathfrak{t}}\lt \rho _{\mathfrak{s}}$
.
$\rho _{\mathfrak{t}}\lt \rho _{\mathfrak{s}}$
.
Proof. It suffices to prove the Lemma for
![]() $\mathfrak{t}=P(\mathfrak{s})$
. Hence we first want to show that
$\mathfrak{t}=P(\mathfrak{s})$
. Hence we first want to show that
![]() $\min _{r\in P(\mathfrak{s})}v(r-w_{\mathfrak{s}})=\rho _{P(\mathfrak{s})}$
and
$\min _{r\in P(\mathfrak{s})}v(r-w_{\mathfrak{s}})=\rho _{P(\mathfrak{s})}$
and
![]() $\rho _{P(\mathfrak{s})}\leq \rho _{\mathfrak{s}}$
. Note that
$\rho _{P(\mathfrak{s})}\leq \rho _{\mathfrak{s}}$
. Note that
Moreover,
If
![]() $r\in \mathfrak{s}$
then
$r\in \mathfrak{s}$
then
![]() $v(w_{\mathfrak{s}}-r)\geq \rho _{\mathfrak{s}}$
, by definition of
$v(w_{\mathfrak{s}}-r)\geq \rho _{\mathfrak{s}}$
, by definition of
![]() $\rho _{\mathfrak{s}}$
. On the other hand, if
$\rho _{\mathfrak{s}}$
. On the other hand, if
![]() $r\in P(\mathfrak{s})\smallsetminus \mathfrak{s}$
then fixing
$r\in P(\mathfrak{s})\smallsetminus \mathfrak{s}$
then fixing
![]() $r'\in \mathfrak{s}$
we have
$r'\in \mathfrak{s}$
we have
by the previous lemma. Thus
![]() $\min _{r\in P(\mathfrak{s})}v(r-w_{\mathfrak{s}})=\rho _{P(\mathfrak{s})}$
, as required.
$\min _{r\in P(\mathfrak{s})}v(r-w_{\mathfrak{s}})=\rho _{P(\mathfrak{s})}$
, as required.
Now suppose
![]() $\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
with
$\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
with
![]() $\mathfrak{t}\supsetneq \mathfrak{s}$
. From Definition 3.8, it follows that
$\mathfrak{t}\supsetneq \mathfrak{s}$
. From Definition 3.8, it follows that
as
![]() $w_{\mathfrak{s}}$
is a rational centre of
$w_{\mathfrak{s}}$
is a rational centre of
![]() $\mathfrak{t}$
. Thus
$\mathfrak{t}$
. Thus
![]() $\rho _{\mathfrak{t}}\lt \rho _{\mathfrak{s}}$
.
$\rho _{\mathfrak{t}}\lt \rho _{\mathfrak{s}}$
.
Definition 3.15.
We say that a proper rational cluster
![]() $\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
is (rationally) minimal if it does not have any proper rational child.
$\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
is (rationally) minimal if it does not have any proper rational child.
From Lemma 3.14 it follows that if
![]() $W\subseteq K$
such that every minimal rational cluster has a rational centre in
$W\subseteq K$
such that every minimal rational cluster has a rational centre in
![]() $W$
, then all clusters have a rational centre in
$W$
, then all clusters have a rational centre in
![]() $W$
. This fact will be key for the construction of the model in Section 5. Another important result is Lemma 3.18, that describes the depth and the radius of
$W$
. This fact will be key for the construction of the model in Section 5. Another important result is Lemma 3.18, that describes the depth and the radius of
![]() $\mathfrak{s}\wedge \mathfrak{s}^{\prime}$
for two rational clusters
$\mathfrak{s}\wedge \mathfrak{s}^{\prime}$
for two rational clusters
![]() $\mathfrak{s},\mathfrak{s}^{\prime}$
. To prove it, we need the following two lemmas.
$\mathfrak{s},\mathfrak{s}^{\prime}$
. To prove it, we need the following two lemmas.
Lemma 3.16.
Every cluster
![]() $\mathfrak{s}$
with
$\mathfrak{s}$
with
![]() $\rho _{\mathfrak{s}}\lt d_{\mathfrak{s}}$
has no rational subcluster
$\rho _{\mathfrak{s}}\lt d_{\mathfrak{s}}$
has no rational subcluster
![]() $\mathfrak{s}^{\prime}\subsetneq \mathfrak{s}$
.
$\mathfrak{s}^{\prime}\subsetneq \mathfrak{s}$
.
Proof. Suppose by contradiction there exists
![]() $\mathfrak{s}^{\prime}\in \Sigma _C^{\textrm{rat}}$
,
$\mathfrak{s}^{\prime}\in \Sigma _C^{\textrm{rat}}$
,
![]() $\mathfrak{s}^{\prime}\subsetneq \mathfrak{s}$
, and fix a rational centre
$\mathfrak{s}^{\prime}\subsetneq \mathfrak{s}$
, and fix a rational centre
![]() $w_{\mathfrak{s}^{\prime}}$
of
$w_{\mathfrak{s}^{\prime}}$
of
![]() $\mathfrak{s}^{\prime}$
. Then
$\mathfrak{s}^{\prime}$
. Then
![]() $w_{\mathfrak{s}^{\prime}}$
is a rational centre of
$w_{\mathfrak{s}^{\prime}}$
is a rational centre of
![]() $\mathfrak{s}$
by the previous lemma. If
$\mathfrak{s}$
by the previous lemma. If
![]() $|\mathfrak{s}^{\prime}|=1$
, then
$|\mathfrak{s}^{\prime}|=1$
, then
![]() $w_{\mathfrak{s}^{\prime}}$
is also a centre of
$w_{\mathfrak{s}^{\prime}}$
is also a centre of
![]() $\mathfrak{s}$
and this contradicts
$\mathfrak{s}$
and this contradicts
![]() $\rho _{\mathfrak{s}}\lt d_{\mathfrak{s}}$
; so, assume
$\rho _{\mathfrak{s}}\lt d_{\mathfrak{s}}$
; so, assume
![]() $\mathfrak{s}^{\prime}$
proper. Let
$\mathfrak{s}^{\prime}$
proper. Let
![]() $r'\in \mathfrak{s}^{\prime}$
such that
$r'\in \mathfrak{s}^{\prime}$
such that
![]() $v(r'-w_{\mathfrak{s}^{\prime}})=\rho _{\mathfrak{s}^{\prime}}$
and
$v(r'-w_{\mathfrak{s}^{\prime}})=\rho _{\mathfrak{s}^{\prime}}$
and
![]() $r\in \mathfrak{s}$
such that
$r\in \mathfrak{s}$
such that
![]() $v(r-w_{\mathfrak{s}^{\prime}})=\rho _{\mathfrak{s}}$
. But then
$v(r-w_{\mathfrak{s}^{\prime}})=\rho _{\mathfrak{s}}$
. But then
![]() $d_{\mathfrak{s}}\leq v(r-w_{\mathfrak{s}^{\prime}}+w_{\mathfrak{s}^{\prime}}-r')=\rho _{\mathfrak{s}}$
again by Lemma 3.14.
$d_{\mathfrak{s}}\leq v(r-w_{\mathfrak{s}^{\prime}}+w_{\mathfrak{s}^{\prime}}-r')=\rho _{\mathfrak{s}}$
again by Lemma 3.14.
In particular, the Lemma above shows that if
![]() $\mathfrak{s}\in \Sigma _f$
and
$\mathfrak{s}\in \Sigma _f$
and
![]() $\mathfrak{s}^{\prime}\in \Sigma _f^{\textrm{rat}}$
is a maximal rational subcluster of
$\mathfrak{s}^{\prime}\in \Sigma _f^{\textrm{rat}}$
is a maximal rational subcluster of
![]() $\mathfrak{s}$
, with
$\mathfrak{s}$
, with
![]() $\mathfrak{s}^{\prime}\subsetneq \mathfrak{s}$
, then
$\mathfrak{s}^{\prime}\subsetneq \mathfrak{s}$
, then
![]() $\mathfrak{s}^{\prime}$
is a child of
$\mathfrak{s}^{\prime}$
is a child of
![]() $\mathfrak{s}$
. Moreover, the parent of a rational cluster is rational.
$\mathfrak{s}$
. Moreover, the parent of a rational cluster is rational.
Lemma 3.17.
Let
![]() $\mathfrak{s},\mathfrak{s}^{\prime}\in \Sigma _f^{\textrm{rat}}$
such that
$\mathfrak{s},\mathfrak{s}^{\prime}\in \Sigma _f^{\textrm{rat}}$
such that
![]() $\mathfrak{s}^{\prime}\nsubseteq \mathfrak{s}$
. If
$\mathfrak{s}^{\prime}\nsubseteq \mathfrak{s}$
. If
![]() $w_{\mathfrak{s}}$
is a rational centre of
$w_{\mathfrak{s}}$
is a rational centre of
![]() $\mathfrak{s}$
then
$\mathfrak{s}$
then
Proof. By Lemma 3.14 we have
Therefore
![]() $\min _{r\in \mathfrak{s}^{\prime}}v(w_{\mathfrak{s}}-r)\geq \rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
. Suppose by contradiction that
$\min _{r\in \mathfrak{s}^{\prime}}v(w_{\mathfrak{s}}-r)\geq \rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
. Suppose by contradiction that
It follows from Lemma 3.14 that
as
![]() $\mathfrak{s}^{\prime}\nsubseteq \mathfrak{s}$
. But then there exists
$\mathfrak{s}^{\prime}\nsubseteq \mathfrak{s}$
. But then there exists
![]() $ \tilde{r}\in (\mathfrak{s}\wedge \mathfrak{s}^{\prime})\smallsetminus (\mathfrak{s}\cup \mathfrak{s}^{\prime})$
such that
$ \tilde{r}\in (\mathfrak{s}\wedge \mathfrak{s}^{\prime})\smallsetminus (\mathfrak{s}\cup \mathfrak{s}^{\prime})$
such that
![]() $v(\tilde{r}-w_{\mathfrak{s}})=\rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
. Consider the rational cluster
$v(\tilde{r}-w_{\mathfrak{s}})=\rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
. Consider the rational cluster
Then
![]() $\mathfrak{s},\mathfrak{s}^{\prime}\subseteq \mathfrak{t}$
, but since
$\mathfrak{s},\mathfrak{s}^{\prime}\subseteq \mathfrak{t}$
, but since
![]() $\tilde{r}\notin \mathfrak{t}$
we have
$\tilde{r}\notin \mathfrak{t}$
we have
![]() $\mathfrak{s}\wedge \mathfrak{s}^{\prime}\nsubseteq \mathfrak{t}$
that contradicts the minimality of
$\mathfrak{s}\wedge \mathfrak{s}^{\prime}\nsubseteq \mathfrak{t}$
that contradicts the minimality of
![]() $\mathfrak{s}\wedge \mathfrak{s}^{\prime}$
.
$\mathfrak{s}\wedge \mathfrak{s}^{\prime}$
.
Lemma 3.18.
Let
![]() $\mathfrak{t}\in \Sigma _f$
with at least two children in
$\mathfrak{t}\in \Sigma _f$
with at least two children in
![]() $\Sigma _f^{\textrm{rat}}$
. Then
$\Sigma _f^{\textrm{rat}}$
. Then
![]() $d_{\mathfrak{t}}=\rho _{\mathfrak{t}}\in \mathbb{Z}$
and
$d_{\mathfrak{t}}=\rho _{\mathfrak{t}}\in \mathbb{Z}$
and
![]() $\mathfrak{t}\in \Sigma _f^{\textrm{rat}}$
. More precisely, if
$\mathfrak{t}\in \Sigma _f^{\textrm{rat}}$
. More precisely, if
![]() $\mathfrak{s},\mathfrak{s}^{\prime}\in \Sigma _f^{\textrm{rat}}$
such that
$\mathfrak{s},\mathfrak{s}^{\prime}\in \Sigma _f^{\textrm{rat}}$
such that
![]() $\mathfrak{s}\subsetneq \mathfrak{s}\wedge \mathfrak{s}^{\prime}\supsetneq \mathfrak{s}^{\prime}$
, then
$\mathfrak{s}\subsetneq \mathfrak{s}\wedge \mathfrak{s}^{\prime}\supsetneq \mathfrak{s}^{\prime}$
, then
where
![]() $w_{\mathfrak{s}}$
and
$w_{\mathfrak{s}}$
and
![]() $w_{\mathfrak{s}^{\prime}}$
are rational centres of
$w_{\mathfrak{s}^{\prime}}$
are rational centres of
![]() $\mathfrak{s}$
and
$\mathfrak{s}$
and
![]() $\mathfrak{s}^{\prime}$
respectively.
$\mathfrak{s}^{\prime}$
respectively.
Proof. If
![]() $d_{\mathfrak{t}}=\rho _{\mathfrak{t}}$
, then
$d_{\mathfrak{t}}=\rho _{\mathfrak{t}}$
, then
![]() $\mathfrak{t}\in \Sigma _f^{\textrm{rat}}$
by Remark 3.13. Hence it suffices to prove the second statement as
$\mathfrak{t}\in \Sigma _f^{\textrm{rat}}$
by Remark 3.13. Hence it suffices to prove the second statement as
![]() $v(w_{\mathfrak{s}}-w_{\mathfrak{s}^{\prime}})\in \mathbb{Z}$
. For our assumptions
$v(w_{\mathfrak{s}}-w_{\mathfrak{s}^{\prime}})\in \mathbb{Z}$
. For our assumptions
![]() $\mathfrak{s}^{\prime}\not \subseteq \mathfrak{s}$
. Then by Lemma 3.17 there exists
$\mathfrak{s}^{\prime}\not \subseteq \mathfrak{s}$
. Then by Lemma 3.17 there exists
![]() $r\in \mathfrak{s}^{\prime}$
so that
$r\in \mathfrak{s}^{\prime}$
so that
![]() $v(r-w_{\mathfrak{s}})=\rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
. Thus,
$v(r-w_{\mathfrak{s}})=\rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
. Thus,
as
![]() $v(r-w_{\mathfrak{s}^{\prime}})\geq \rho _{\mathfrak{s}^{\prime}}\gt \rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
by Lemma 3.14. Finally,
$v(r-w_{\mathfrak{s}^{\prime}})\geq \rho _{\mathfrak{s}^{\prime}}\gt \rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
by Lemma 3.14. Finally,
![]() $d_{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}=\rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
follows from Lemma 3.16.
$d_{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}=\rho _{\mathfrak{s}\wedge \mathfrak{s}^{\prime}}$
follows from Lemma 3.16.
Definition 3.19.
For a proper cluster
![]() $\mathfrak{s}$
set
$\mathfrak{s}$
set
Example 3.20.
Let
![]() $f=x^{11}-3x^6+9x^5-27\in \mathbb{Q}_3[x]$
. The set of roots of
$f=x^{11}-3x^6+9x^5-27\in \mathbb{Q}_3[x]$
. The set of roots of
![]() $f$
is
$f$
is
where
![]() $\zeta _q$
is a primitive
$\zeta _q$
is a primitive
![]() $q$
th root of unity for
$q$
th root of unity for
![]() $q=3,5$
. Then the proper clusters of
$q=3,5$
. Then the proper clusters of
![]() $f$
are
$f$
are
with
![]() $d_{{\mathfrak{s}}_1}=d_{{\mathfrak{s}}_2}=\frac{5}{6}$
,
$d_{{\mathfrak{s}}_1}=d_{{\mathfrak{s}}_2}=\frac{5}{6}$
,
![]() $d_{{\mathfrak{s}}_3}=\frac{1}{3}$
and
$d_{{\mathfrak{s}}_3}=\frac{1}{3}$
and
![]() $d_{\mathfrak{R}}=\frac{1}{5}$
. The graphic representation of the cluster picture of
$d_{\mathfrak{R}}=\frac{1}{5}$
. The graphic representation of the cluster picture of
![]() $f$
is then
$f$
is then

where the subscripts of clusters (represented as circles) are their depths.
Furthermore, note that
![]() $0$
is a rational centre for all proper clusters and we have
$0$
is a rational centre for all proper clusters and we have
![]() $\rho _{{\mathfrak{s}}_1}=\rho _{{\mathfrak{s}}_2}=\rho _{{\mathfrak{s}}_3}=\frac{1}{3}$
and
$\rho _{{\mathfrak{s}}_1}=\rho _{{\mathfrak{s}}_2}=\rho _{{\mathfrak{s}}_3}=\frac{1}{3}$
and
![]() $\rho _{\mathfrak{R}}=\frac{1}{5}$
.
$\rho _{\mathfrak{R}}=\frac{1}{5}$
.
Finally, for every cluster
![]() $\mathfrak{s}$
we can also compute
$\mathfrak{s}$
we can also compute
![]() $\nu _{\mathfrak{s}}$
and
$\nu _{\mathfrak{s}}$
and
![]() $\epsilon _{\mathfrak{s}}$
, that are
$\epsilon _{\mathfrak{s}}$
, that are
Example 3.21.
Let
![]() $f=x^9+12x^6+36x^3+81\in \mathbb{Q}_3[x]$
and fix an isomorphism
$f=x^9+12x^6+36x^3+81\in \mathbb{Q}_3[x]$
and fix an isomorphism
![]() ${\overline{\mathbb{Q}}}_3\simeq{\mathbb{C}}$
. Then the set of roots of
${\overline{\mathbb{Q}}}_3\simeq{\mathbb{C}}$
. Then the set of roots of
![]() $f$
is
$f$
is
where
![]() $\zeta _q=e^{2\pi i/q}$
is a primitive
$\zeta _q=e^{2\pi i/q}$
is a primitive
![]() $q$
th root of unity for
$q$
th root of unity for
![]() $q=3,9$
. Then the proper clusters of
$q=3,9$
. Then the proper clusters of
![]() $f$
are
$f$
are
with
![]() $d_{{\mathfrak{s}}_1}=\frac{7}{6}$
,
$d_{{\mathfrak{s}}_1}=\frac{7}{6}$
,
![]() $d_{{\mathfrak{s}}_2}=d_{{\mathfrak{s}}_3}=\frac{5}{6}$
,
$d_{{\mathfrak{s}}_2}=d_{{\mathfrak{s}}_3}=\frac{5}{6}$
,
![]() $d_{{\mathfrak{s}}_4}=\frac{1}{2}$
, and
$d_{{\mathfrak{s}}_4}=\frac{1}{2}$
, and
![]() $d_{\mathfrak{R}}=\frac{1}{3}$
. The cluster picture of
$d_{\mathfrak{R}}=\frac{1}{3}$
. The cluster picture of
![]() $f$
is then
$f$
is then

It is easy to see that
![]() $0$
is a rational centre for all proper clusters and that
$0$
is a rational centre for all proper clusters and that
![]() $\rho _{{\mathfrak{s}}_1}=\frac{2}{3}$
,
$\rho _{{\mathfrak{s}}_1}=\frac{2}{3}$
,
![]() $\rho _{{\mathfrak{s}}_2}=\rho _{{\mathfrak{s}}_3}=\rho _{{\mathfrak{s}}_4}=\rho _{\mathfrak{R}}=\frac{1}{3}$
. Finally,
$\rho _{{\mathfrak{s}}_2}=\rho _{{\mathfrak{s}}_3}=\rho _{{\mathfrak{s}}_4}=\rho _{\mathfrak{R}}=\frac{1}{3}$
. Finally,
The goal of this section is to describe the
![]() $\texttt{NP}$
-regularity of
$\texttt{NP}$
-regularity of
![]() $f\in K[x]$
(and its translations) in terms of conditions on its cluster picture.
$f\in K[x]$
(and its translations) in terms of conditions on its cluster picture.
Notation 3.22.
If
![]() $p\gt 0$
, we denote by
$p\gt 0$
, we denote by
![]() $|\cdot |_p$
the standard
$|\cdot |_p$
the standard
![]() $p$
-adic absolute value attached to
$p$
-adic absolute value attached to
![]() $\mathbb{Q}$
, that is
$\mathbb{Q}$
, that is
![]() $|a|_p=p^{-v_p(a)}$
for all
$|a|_p=p^{-v_p(a)}$
for all
![]() $a\in \mathbb{Q}$
. If
$a\in \mathbb{Q}$
. If
![]() $p=0$
, then we write
$p=0$
, then we write
![]() $|\cdot |_p$
for the function on
$|\cdot |_p$
for the function on
![]() $\mathbb{Q}$
identically equal to
$\mathbb{Q}$
identically equal to
![]() $1$
, that is
$1$
, that is
![]() $|a|_p=1$
for all
$|a|_p=1$
for all
![]() $a\in \mathbb{Q}$
.
$a\in \mathbb{Q}$
.
Lemma 3.23.
Suppose that
![]() $x\nmid f$
and that
$x\nmid f$
and that
![]() $\texttt{NP}(f)$
is a segment
$\texttt{NP}(f)$
is a segment
![]() $L$
of slope
$L$
of slope
![]() $-\rho$
. Let
$-\rho$
. Let
![]() $n$
be the denominator of
$n$
be the denominator of
![]() $\rho$
. Then
$\rho$
. Then
![]() $f$
is
$f$
is
![]() $\texttt{NP}$
-regular if and only if all proper clusters
$\texttt{NP}$
-regular if and only if all proper clusters
![]() $\mathfrak{s}\in \Sigma _f$
with
$\mathfrak{s}\in \Sigma _f$
with
![]() $|\mathfrak{s}|\gt |\rho |_p$
satisfy
$|\mathfrak{s}|\gt |\rho |_p$
satisfy
![]() $d_{\mathfrak{s}}=\rho$
.
$d_{\mathfrak{s}}=\rho$
.
More precisely:
-
(i) If
 $\mathfrak{s}\in \Sigma _f$
with
$\mathfrak{s}\in \Sigma _f$
with
 $|\mathfrak{s}|\gt |\rho |_p$
but
$|\mathfrak{s}|\gt |\rho |_p$
but
 $d_{\mathfrak{s}}\gt \rho$
, then
$d_{\mathfrak{s}}\gt \rho$
, then
 $\overline{f|_L}$
has a non-zero multiple root
$\overline{f|_L}$
has a non-zero multiple root
 $\bar{u}=\frac{r^n}{\pi ^{n\rho }} \mod \pi$
, for some (any)
$\bar{u}=\frac{r^n}{\pi ^{n\rho }} \mod \pi$
, for some (any)
 $r\in \mathfrak{s}$
.
$r\in \mathfrak{s}$
. -
(ii) The multiplicity of a root
 $\bar{u}\in \bar{k}^\times$
of
$\bar{u}\in \bar{k}^\times$
of
 $\overline{f|_L}$
equals
$\overline{f|_L}$
equals
 $|{\mathfrak{s}}^0|/n$
, where
$|{\mathfrak{s}}^0|/n$
, where
 \begin{align*}{\mathfrak{s}}^0=\left \{r\in \mathfrak{R}\mid \bar{u}=\tfrac{r^n}{\pi ^{n\rho }}\mod \pi \right \}. \end{align*}
\begin{align*}{\mathfrak{s}}^0=\left \{r\in \mathfrak{R}\mid \bar{u}=\tfrac{r^n}{\pi ^{n\rho }}\mod \pi \right \}. \end{align*}
-
(iii) All multiple roots of
 $\overline{f|_L}$
come from clusters
$\overline{f|_L}$
come from clusters
 $\mathfrak{s}$
as described in (i).
$\mathfrak{s}$
as described in (i).
Proof. Let
![]() $q$
be the highest power of
$q$
be the highest power of
![]() $p$
dividing
$p$
dividing
![]() $n$
(set
$n$
(set
![]() $q=1$
if
$q=1$
if
![]() $p=0$
). Let
$p=0$
). Let
![]() $m=n/q$
so that
$m=n/q$
so that
![]() $p\nmid m$
. Let
$p\nmid m$
. Let
![]() $\mathfrak{R}=\{r_i\mid i=1,\dots,D\}$
be the (multi-)set of roots of
$\mathfrak{R}=\{r_i\mid i=1,\dots,D\}$
be the (multi-)set of roots of
![]() $f$
, where
$f$
, where
![]() $D\;:\!=\;\deg f$
. Fix some choice of
$D\;:\!=\;\deg f$
. Fix some choice of
![]() $\sqrt [n]{\pi }$
and define
$\sqrt [n]{\pi }$
and define
![]() $\bar{u}_i\in \bar{k}^\times$
as
$\bar{u}_i\in \bar{k}^\times$
as
![]() $\bar{u}_i=r_i/\pi ^\rho \mod \pi$
, for all
$\bar{u}_i=r_i/\pi ^\rho \mod \pi$
, for all
![]() $i=1,\dots, D$
. Firstly, note that there exists a proper cluster
$i=1,\dots, D$
. Firstly, note that there exists a proper cluster
![]() $\mathfrak{s}$
with
$\mathfrak{s}$
with
![]() $|\mathfrak{s}|\gt |\rho |_p$
and
$|\mathfrak{s}|\gt |\rho |_p$
and
![]() $d_{\mathfrak{s}}\gt \rho$
if and only if there exists a subset
$d_{\mathfrak{s}}\gt \rho$
if and only if there exists a subset
![]() $I\subseteq \{1,\dots,D\}$
of size
$I\subseteq \{1,\dots,D\}$
of size
![]() $|I|\gt q$
such that
$|I|\gt q$
such that
![]() $\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
$\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
![]() $i_1,i_2\in I$
. Indeed, given
$i_1,i_2\in I$
. Indeed, given
![]() $\mathfrak{s}$
, then
$\mathfrak{s}$
, then
![]() $I=\{i\in \{1,\dots,D\}\mid r_i\in \mathfrak{s}\}$
, while given
$I=\{i\in \{1,\dots,D\}\mid r_i\in \mathfrak{s}\}$
, while given
![]() $I$
, then
$I$
, then
![]() $\mathfrak{s}=\{r_i\mid \bar{u}_i=\bar{u}_{i_0},\text{ for any }i_0\in I\}$
. Secondly, recall that
$\mathfrak{s}=\{r_i\mid \bar{u}_i=\bar{u}_{i_0},\text{ for any }i_0\in I\}$
. Secondly, recall that
![]() $f$
is not
$f$
is not
![]() $\texttt{NP}$
-regular if and only if
$\texttt{NP}$
-regular if and only if
![]() $\overline{f|_L}$
has a multiple root in
$\overline{f|_L}$
has a multiple root in
![]() $\bar{k}^\times$
. Therefore we will prove that
$\bar{k}^\times$
. Therefore we will prove that
![]() $\overline{f|_L}$
has a non-zero multiple root if and only if there exists a subset
$\overline{f|_L}$
has a non-zero multiple root if and only if there exists a subset
![]() $I\subseteq \{1,\dots,D\}$
with size
$I\subseteq \{1,\dots,D\}$
with size
![]() $|I|\gt q$
and such that
$|I|\gt q$
and such that
![]() $\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
$\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
![]() $i_1,i_2\in I$
.
$i_1,i_2\in I$
.
Note that for the lower convexity of
![]() $\texttt{NP}(f)=L$
, we have
$\texttt{NP}(f)=L$
, we have
Hence
![]() $\{\bar{u}_i \mid i=1,\dots,D\}$
is the multiset of roots of
$\{\bar{u}_i \mid i=1,\dots,D\}$
is the multiset of roots of
![]() ${\overline{f|_L}}(x^n)$
. Then there exists an
${\overline{f|_L}}(x^n)$
. Then there exists an
![]() $n$
-to-
$n$
-to-
![]() $1$
map
$1$
map
where
![]() $\{\bar{w}_j\mid j=1,\dots,D/n\}$
is the multiset of roots of
$\{\bar{w}_j\mid j=1,\dots,D/n\}$
is the multiset of roots of
![]() $\overline{f|_L}$
. Note that
$\overline{f|_L}$
. Note that
![]() $\bar{w}_j\neq 0$
for all
$\bar{w}_j\neq 0$
for all
![]() $j=1,\dots,D/n$
, so all roots of
$j=1,\dots,D/n$
, so all roots of
![]() $\overline{f|_L}$
are non-zero.
$\overline{f|_L}$
are non-zero.
Now, suppose that
![]() $f$
is not
$f$
is not
![]() $\texttt{NP}$
-regular. We want to show that there exists a subset
$\texttt{NP}$
-regular. We want to show that there exists a subset
![]() $I\subset \{1,\dots,D\}$
with
$I\subset \{1,\dots,D\}$
with
![]() $|I|\gt q$
such that
$|I|\gt q$
such that
![]() $\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
$\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
![]() $i_1,i_2\in I$
. Since
$i_1,i_2\in I$
. Since
![]() $f$
is not
$f$
is not
![]() $\texttt{NP}$
-regular, its reduction
$\texttt{NP}$
-regular, its reduction
![]() $\overline{f|_L}$
has a (non-zero) multiple root. Then there exist
$\overline{f|_L}$
has a (non-zero) multiple root. Then there exist
![]() $j_1,j_2\in \{1,\dots,D/n\}$
so that
$j_1,j_2\in \{1,\dots,D/n\}$
so that
![]() $\bar{w}_{j_1}=\bar{w}_{j_2}\;=\!:\;\bar{w}$
. Hence, by the definition of
$\bar{w}_{j_1}=\bar{w}_{j_2}\;=\!:\;\bar{w}$
. Hence, by the definition of
![]() $\bar \phi$
, for some (any)
$\bar \phi$
, for some (any)
![]() $\bar{u}\in \bar \phi ^{-1}(\bar{w})$
, there are at least
$\bar{u}\in \bar \phi ^{-1}(\bar{w})$
, there are at least
![]() $2 q$
$2 q$
![]() $\bar{u}_i$
’s with
$\bar{u}_i$
’s with
![]() $\bar{u}_i=\bar{u}$
. Let
$\bar{u}_i=\bar{u}$
. Let
![]() $I$
denote the set of their indices. Then
$I$
denote the set of their indices. Then
![]() $|I|\geq 2q\gt q$
and
$|I|\geq 2q\gt q$
and
![]() $\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
$\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
![]() $i_1,i_2\in I$
, as required.
$i_1,i_2\in I$
, as required.
On the other hand, suppose that there exists a subset
![]() $I\subset \{1,\dots,D\}$
with
$I\subset \{1,\dots,D\}$
with
![]() $|I|\gt q$
and such that
$|I|\gt q$
and such that
![]() $\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
$\bar{u}_{i_1}=\bar{u}_{i_2}$
for all
![]() $i_1,i_2\in I$
. We want to show that
$i_1,i_2\in I$
. We want to show that
![]() $\overline{f|_L}$
has a multiple root, that is there exist two indices
$\overline{f|_L}$
has a multiple root, that is there exist two indices
![]() $j_1,j_2\in \{1,\dots,D/n\}$
such that
$j_1,j_2\in \{1,\dots,D/n\}$
such that
![]() $\bar{w}_{j_1}=\bar{w}_{j_2}$
. Suppose not and let
$\bar{w}_{j_1}=\bar{w}_{j_2}$
. Suppose not and let
![]() $j\in \{1,\dots,D/n\}$
such that
$j\in \{1,\dots,D/n\}$
such that
![]() $\bar{w}_j=\bar{u}_i^m=\bar \phi (\bar{u}_i)$
for some (all)
$\bar{w}_j=\bar{u}_i^m=\bar \phi (\bar{u}_i)$
for some (all)
![]() $i\in I$
. Then the polynomial
$i\in I$
. Then the polynomial
![]() $x^n-\bar{w}_j=(x^m-\bar{w}_j)^{q}\in \bar{k}[x]$
, factor of
$x^n-\bar{w}_j=(x^m-\bar{w}_j)^{q}\in \bar{k}[x]$
, factor of
![]() ${\overline{f|_L}}(x^n)$
, should have a root of order
${\overline{f|_L}}(x^n)$
, should have a root of order
![]() $|I|\gt q$
. This would imply
$|I|\gt q$
. This would imply
![]() $x^m-\bar{w}_j$
is inseparable, a contradiction as
$x^m-\bar{w}_j$
is inseparable, a contradiction as
![]() $p\nmid m$
.
$p\nmid m$
.
The parts (i), (ii) and (iii) of the Lemma follow from above:
-
(i) Given a proper cluster
 $\mathfrak{s}\in \Sigma _f$
with
$\mathfrak{s}\in \Sigma _f$
with
 $|\mathfrak{s}|\gt |\rho |_p$
and
$|\mathfrak{s}|\gt |\rho |_p$
and
 $d_{\mathfrak{s}}\gt \rho$
, we showed that
$d_{\mathfrak{s}}\gt \rho$
, we showed that
 $\overline{f|_L}$
has a non-zero multiple root
$\overline{f|_L}$
has a non-zero multiple root
 $\bar{w}_j=\bar{u}_i^n={r_i^n}/{\pi ^{n\rho }}\mod \pi$
, where
$\bar{w}_j=\bar{u}_i^n={r_i^n}/{\pi ^{n\rho }}\mod \pi$
, where
 $r_i$
is any root in
$r_i$
is any root in
 $\mathfrak{s}$
.
$\mathfrak{s}$
. -
(ii) By the definition of
 $\bar{\phi }$
, given
$\bar{\phi }$
, given
 $\bar{w}\in \bar{k}$
, the number of
$\bar{w}\in \bar{k}$
, the number of
 $\bar{w}_j$
’s such that
$\bar{w}_j$
’s such that
 $\bar{w}_j=\bar{w}$
equals
$\bar{w}_j=\bar{w}$
equals
 $|{\mathfrak{s}}^0|/n$
, where
$|{\mathfrak{s}}^0|/n$
, where
 ${\mathfrak{s}}^0=\{r_i\mid \bar{u}_i^n=\bar{w}\}$
.
${\mathfrak{s}}^0=\{r_i\mid \bar{u}_i^n=\bar{w}\}$
. -
(iii) Given a (non-zero) multiple root
 $\bar{w}$
of
$\bar{w}$
of
 $\overline{f|_L}$
we showed that there exists
$\overline{f|_L}$
we showed that there exists
 $I\subseteq \{1,\dots,D\}$
, with
$I\subseteq \{1,\dots,D\}$
, with
 $|I|\gt q$
and
$|I|\gt q$
and
 $\bar{u}_{i_1}=\bar{u}_{i_2}$
for any
$\bar{u}_{i_1}=\bar{u}_{i_2}$
for any
 $i_1,i_2\in I$
, such that
$i_1,i_2\in I$
, such that
 $\bar{u}_i^n=\bar{w}$
for all
$\bar{u}_i^n=\bar{w}$
for all
 $i\in I$
. The set
$i\in I$
. The set
 $\mathfrak{s}=\{r_i\mid \bar{u}_i=\bar{u}_{i_0},\text{ for any }i_0\in I\}$
is a proper cluster as in (i).
$\mathfrak{s}=\{r_i\mid \bar{u}_i=\bar{u}_{i_0},\text{ for any }i_0\in I\}$
is a proper cluster as in (i).
Theorem 3.24.
Let
![]() $w\in K$
and
$w\in K$
and
![]() $f_w(x)=f(x+w)$
. For all clusters
$f_w(x)=f(x+w)$
. For all clusters
![]() $\mathfrak{s}\in \Sigma _f$
define
$\mathfrak{s}\in \Sigma _f$
define
![]() $\lambda _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w)$
, and let
$\lambda _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w)$
, and let
![]() $b$
be the denominator of
$b$
be the denominator of
![]() $\lambda _{\mathfrak{s}}$
. Then
$\lambda _{\mathfrak{s}}$
. Then
![]() $f_w$
is
$f_w$
is
![]() $\texttt{NP}$
-regular if and only if all proper clusters
$\texttt{NP}$
-regular if and only if all proper clusters
![]() $\mathfrak{s}\in \Sigma _f$
with
$\mathfrak{s}\in \Sigma _f$
with
![]() $|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
have
$|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
have
![]() $d_{\mathfrak{s}}=\lambda _{\mathfrak{s}}$
.
$d_{\mathfrak{s}}=\lambda _{\mathfrak{s}}$
.
More precisely:
-
(i) Let
 $\mathfrak{s}\in \Sigma _f$
with
$\mathfrak{s}\in \Sigma _f$
with
 $|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
but
$|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
but
 $d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
, and let
$d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
, and let
 $r\in \mathfrak{s}$
with
$r\in \mathfrak{s}$
with
 $v(r-w)=\lambda _{\mathfrak{s}}$
. Then
$v(r-w)=\lambda _{\mathfrak{s}}$
. Then
 $\overline{f_w|_L}$
has a non-zero multiple root
$\overline{f_w|_L}$
has a non-zero multiple root
 $\bar{u}=\frac{(r-w)^b}{\pi ^{b\lambda _{\mathfrak{s}}}}\mod \pi$
, where
$\bar{u}=\frac{(r-w)^b}{\pi ^{b\lambda _{\mathfrak{s}}}}\mod \pi$
, where
 $L$
is the edge of
$L$
is the edge of
 $\texttt{NP}(f_w)$
of slope
$\texttt{NP}(f_w)$
of slope
 $-\lambda _{\mathfrak{s}}$
.
$-\lambda _{\mathfrak{s}}$
. -
(ii) Let
 $L$
be an edge of
$L$
be an edge of
 $\texttt{NP}(f_w)$
of slope
$\texttt{NP}(f_w)$
of slope
 $-\lambda$
. Let
$-\lambda$
. Let
 $l$
be the denominator of
$l$
be the denominator of
 $\lambda$
. The multiplicity of a root
$\lambda$
. The multiplicity of a root
 $\bar{u}\in \bar{k}^\times$
of
$\bar{u}\in \bar{k}^\times$
of
 $\overline{f_w|_L}$
equals
$\overline{f_w|_L}$
equals
 $|{\mathfrak{s}}^0|/l$
, where
$|{\mathfrak{s}}^0|/l$
, where
 \begin{align*}{\mathfrak{s}}^0=\big \{r\in \mathfrak{R}\mid v(r-w)=\lambda \quad \text{and}\quad \bar{u}=\tfrac{(r-w)^l}{\pi ^{l\lambda }}\mod \pi \big \}. \end{align*}
\begin{align*}{\mathfrak{s}}^0=\big \{r\in \mathfrak{R}\mid v(r-w)=\lambda \quad \text{and}\quad \bar{u}=\tfrac{(r-w)^l}{\pi ^{l\lambda }}\mod \pi \big \}. \end{align*}
-
(iii) For every edge
 $L$
of
$L$
of
 $\texttt{NP}(f_w)$
, the multiple roots of
$\texttt{NP}(f_w)$
, the multiple roots of
 $\overline{f_w|_L}$
come from proper clusters
$\overline{f_w|_L}$
come from proper clusters
 $\mathfrak{s}$
for
$\mathfrak{s}$
for
 $f$
as described in (i).
$f$
as described in (i).
Proof. Let
![]() $\mathfrak{R}_w$
be the set of roots of
$\mathfrak{R}_w$
be the set of roots of
![]() $f_w$
. Note that we have a natural bijection
$f_w$
. Note that we have a natural bijection
![]() $\mathfrak{R}\rightarrow \mathfrak{R}_w$
,
$\mathfrak{R}\rightarrow \mathfrak{R}_w$
,
![]() $r\mapsto r-w$
, which induces a bijective function
$r\mapsto r-w$
, which induces a bijective function
![]() $\psi :\Sigma _{f}\rightarrow \Sigma _{f_w}$
, sending
$\psi :\Sigma _{f}\rightarrow \Sigma _{f_w}$
, sending
In particular, if
![]() $\mathfrak{s}\in \Sigma _{f}$
,
$\mathfrak{s}\in \Sigma _{f}$
,
![]() $|\mathfrak{s}|=|\psi (\mathfrak{s})|$
,
$|\mathfrak{s}|=|\psi (\mathfrak{s})|$
,
![]() $d_{\mathfrak{s}}=d_{\psi (\mathfrak{s})}$
and
$d_{\mathfrak{s}}=d_{\psi (\mathfrak{s})}$
and
Hence it suffices to show the theorem for
![]() $w=0$
.
$w=0$
.
Assume
![]() $w=0$
. Let
$w=0$
. Let
![]() $f=c_f\cdot g_0\cdot g_1\dots g_t$
be a factorisation of Theorem 2.2. Note that if
$f=c_f\cdot g_0\cdot g_1\dots g_t$
be a factorisation of Theorem 2.2. Note that if
![]() $t=0$
, then either
$t=0$
, then either
![]() $f\in K$
or
$f\in K$
or
![]() $f\in Kx$
. In both cases,
$f\in Kx$
. In both cases,
![]() $f$
is clearly
$f$
is clearly
![]() $\texttt{NP}$
-regular and has no proper clusters. Then assume
$\texttt{NP}$
-regular and has no proper clusters. Then assume
![]() $t\gt 0$
and let
$t\gt 0$
and let
![]() $-\rho _i$
be the slope of
$-\rho _i$
be the slope of
![]() $\texttt{NP}(g_i)$
for any
$\texttt{NP}(g_i)$
for any
![]() $i=1,\dots,t$
. Denote by
$i=1,\dots,t$
. Denote by
![]() $\mathfrak{R}$
the set of roots of
$\mathfrak{R}$
the set of roots of
![]() $f$
and by
$f$
and by
![]() $\mathfrak{R}_i$
the set of roots of
$\mathfrak{R}_i$
the set of roots of
![]() $g_i$
for
$g_i$
for
![]() $i=0,\dots,t$
. Note that the
$i=0,\dots,t$
. Note that the
![]() $\mathfrak{R}_i$
’s are pairwise disjoint. From Remark 2.7, for every edge
$\mathfrak{R}_i$
’s are pairwise disjoint. From Remark 2.7, for every edge
![]() $L$
of
$L$
of
![]() $\texttt{NP}(f)$
there exists
$\texttt{NP}(f)$
there exists
![]() $i$
such that
$i$
such that
![]() ${\overline{f|_L}}=\bar{c}_i\cdot{\overline{g_i|_{\texttt{NP}(g_i)}}}$
for some
${\overline{f|_L}}=\bar{c}_i\cdot{\overline{g_i|_{\texttt{NP}(g_i)}}}$
for some
![]() $\bar{c}_i\in k^\times$
. Hence, by Lemma 2.9 and Lemma 3.23, we need to prove that there exists a proper cluster
$\bar{c}_i\in k^\times$
. Hence, by Lemma 2.9 and Lemma 3.23, we need to prove that there exists a proper cluster
![]() $\mathfrak{s}\in \Sigma _f$
such that
$\mathfrak{s}\in \Sigma _f$
such that
![]() $|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
and
$|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
and
![]() $d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
if and only if for some
$d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
if and only if for some
![]() $i=1,\dots,t$
there exists a proper cluster
$i=1,\dots,t$
there exists a proper cluster
![]() ${\mathfrak{s}}_i\in \Sigma _{g_i}$
such that
${\mathfrak{s}}_i\in \Sigma _{g_i}$
such that
![]() $|{\mathfrak{s}}_i|\gt |\lambda _{{\mathfrak{s}}_i}|_p=|\rho _i|_p$
and
$|{\mathfrak{s}}_i|\gt |\lambda _{{\mathfrak{s}}_i}|_p=|\rho _i|_p$
and
![]() $d_{{\mathfrak{s}}_i}\gt \lambda _{{\mathfrak{s}}_i}=\rho _i$
. We will show that one can choose
$d_{{\mathfrak{s}}_i}\gt \lambda _{{\mathfrak{s}}_i}=\rho _i$
. We will show that one can choose
![]() $\mathfrak{s}={\mathfrak{s}}_i$
.
$\mathfrak{s}={\mathfrak{s}}_i$
.
First, note that if
![]() $\mathfrak{s}$
is a proper cluster, then
$\mathfrak{s}$
is a proper cluster, then
![]() $\mathfrak{s}\not \subseteq \mathfrak{R}_0$
, as
$\mathfrak{s}\not \subseteq \mathfrak{R}_0$
, as
![]() $|\mathfrak{R}_0|\leq 1$
. Furthermore, if
$|\mathfrak{R}_0|\leq 1$
. Furthermore, if
![]() $\mathfrak{s}\in \Sigma _f$
contains roots of different valuations, that is
$\mathfrak{s}\in \Sigma _f$
contains roots of different valuations, that is
![]() $\mathfrak{s}\nsubseteq \mathfrak{R}_i$
for all
$\mathfrak{s}\nsubseteq \mathfrak{R}_i$
for all
![]() $i$
, then
$i$
, then
Now suppose there exists a proper cluster
![]() $\mathfrak{s}\in \Sigma _f$
such that
$\mathfrak{s}\in \Sigma _f$
such that
![]() $|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
and
$|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
and
![]() $d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
. For the observation above, the inequality
$d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
. For the observation above, the inequality
![]() $d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
implies that
$d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
implies that
![]() $\mathfrak{s}\subseteq \mathfrak{R}_i$
for some
$\mathfrak{s}\subseteq \mathfrak{R}_i$
for some
![]() $i=1,\dots,t$
. Let
$i=1,\dots,t$
. Let
![]() $\mathcal{D}$
be the
$\mathcal{D}$
be the
![]() $v$
-adic disc such that
$v$
-adic disc such that
![]() $\mathfrak{s}=\mathcal{D}\cap \mathfrak{R}$
. Since
$\mathfrak{s}=\mathcal{D}\cap \mathfrak{R}$
. Since
![]() $\mathfrak{s}\subseteq \mathfrak{R}_i$
, one has
$\mathfrak{s}\subseteq \mathfrak{R}_i$
, one has
![]() $\mathfrak{s}=\mathcal{D}\cap \mathfrak{R}_i$
which means that
$\mathfrak{s}=\mathcal{D}\cap \mathfrak{R}_i$
which means that
![]() $\mathfrak{s}\in \Sigma _{g_i}$
, as required.
$\mathfrak{s}\in \Sigma _{g_i}$
, as required.
Finally suppose that for some
![]() $i=1,\dots,s$
, there exists a proper cluster
$i=1,\dots,s$
, there exists a proper cluster
![]() ${\mathfrak{s}}_i\in \Sigma _{g_i}$
such that
${\mathfrak{s}}_i\in \Sigma _{g_i}$
such that
![]() $|{\mathfrak{s}}_i|\gt |\rho _i|_p$
and
$|{\mathfrak{s}}_i|\gt |\rho _i|_p$
and
![]() $d_{{\mathfrak{s}}_i}\gt \rho _i$
. Let
$d_{{\mathfrak{s}}_i}\gt \rho _i$
. Let
![]() $r_i\in{\mathfrak{s}}_i$
. Then
$r_i\in{\mathfrak{s}}_i$
. Then
Consider the cluster
![]() $\mathfrak{s}\;:\!=\;\{x\in \bar{K} \mid v(x-r_i)\geq d_{{\mathfrak{s}}_i}\}\cap \mathfrak{R}$
of
$\mathfrak{s}\;:\!=\;\{x\in \bar{K} \mid v(x-r_i)\geq d_{{\mathfrak{s}}_i}\}\cap \mathfrak{R}$
of
![]() $f$
. Clearly
$f$
. Clearly
![]() ${\mathfrak{s}}_i\subseteq \mathfrak{s}$
. Therefore
${\mathfrak{s}}_i\subseteq \mathfrak{s}$
. Therefore
which implies
where
![]() $d_{\mathfrak{s}}=d_{{\mathfrak{s}}_i}$
by construction. Again, from the observation above, the inequality
$d_{\mathfrak{s}}=d_{{\mathfrak{s}}_i}$
by construction. Again, from the observation above, the inequality
![]() $d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
implies that
$d_{\mathfrak{s}}\gt \lambda _{\mathfrak{s}}$
implies that
![]() $\mathfrak{s}$
is contained in
$\mathfrak{s}$
is contained in
![]() $\mathfrak{R}_j$
for some
$\mathfrak{R}_j$
for some
![]() $j$
. As
$j$
. As
![]() $\mathfrak{s}\cap \mathfrak{R}_i\supseteq{\mathfrak{s}}_i\cap \mathfrak{R}_i={\mathfrak{s}}_i$
, we must have
$\mathfrak{s}\cap \mathfrak{R}_i\supseteq{\mathfrak{s}}_i\cap \mathfrak{R}_i={\mathfrak{s}}_i$
, we must have
![]() $\mathfrak{s}\subseteq \mathfrak{R}_i$
. Thus
$\mathfrak{s}\subseteq \mathfrak{R}_i$
. Thus
![]() $\mathfrak{s}={\mathfrak{s}}_i$
, that concludes the proof.
$\mathfrak{s}={\mathfrak{s}}_i$
, that concludes the proof.
Corollary 3.25.
Let
![]() $f\in K[x]$
be a separable polynomial. Let
$f\in K[x]$
be a separable polynomial. Let
![]() $w\in K$
and
$w\in K$
and
![]() $f_w(x)=f(x+w)$
. Then
$f_w(x)=f(x+w)$
. Then
![]() $f_w$
is
$f_w$
is
![]() $\texttt{NP}$
-regular if and only if all proper clusters
$\texttt{NP}$
-regular if and only if all proper clusters
![]() $\mathfrak{s}\in \Sigma _f$
have rational centre
$\mathfrak{s}\in \Sigma _f$
have rational centre
![]() $w$
and those with
$w$
and those with
![]() $|\mathfrak{s}|\gt |\rho _{\mathfrak{s}}|_p$
satisfy
$|\mathfrak{s}|\gt |\rho _{\mathfrak{s}}|_p$
satisfy
![]() $d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
.
$d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
.
Proof. If
![]() $f_w$
is
$f_w$
is
![]() $\texttt{NP}$
-regular, then, from the previous theorem, all proper clusters
$\texttt{NP}$
-regular, then, from the previous theorem, all proper clusters
![]() $\mathfrak{s}\in \Sigma _f$
with
$\mathfrak{s}\in \Sigma _f$
with
![]() $|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
have
$|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
have
![]() $d_{\mathfrak{s}}=\lambda _{\mathfrak{s}}$
, where
$d_{\mathfrak{s}}=\lambda _{\mathfrak{s}}$
, where
![]() $\lambda _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w)$
. First let
$\lambda _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w)$
. First let
![]() $\mathfrak{s}\in \Sigma _f$
proper and assume
$\mathfrak{s}\in \Sigma _f$
proper and assume
![]() $|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
. Then
$|\mathfrak{s}|\gt |\lambda _{\mathfrak{s}}|_p$
. Then
so
![]() $d_{\mathfrak{s}}=\lambda _{\mathfrak{s}}=\rho _{\mathfrak{s}}$
, and
$d_{\mathfrak{s}}=\lambda _{\mathfrak{s}}=\rho _{\mathfrak{s}}$
, and
![]() $w$
is a rational centre of
$w$
is a rational centre of
![]() $\mathfrak{s}$
. Now assume
$\mathfrak{s}$
. Now assume
![]() $|\mathfrak{s}|\leq |\lambda _{\mathfrak{s}}|_p$
. In particular,
$|\mathfrak{s}|\leq |\lambda _{\mathfrak{s}}|_p$
. In particular,
![]() $p\gt 0$
and
$p\gt 0$
and
![]() $\lambda _{\mathfrak{s}}\notin \mathbb{Z}$
, and so
$\lambda _{\mathfrak{s}}\notin \mathbb{Z}$
, and so
where
![]() $w_{\mathfrak{s}}$
is a rational centre of
$w_{\mathfrak{s}}$
is a rational centre of
![]() $\mathfrak{s}$
. Let
$\mathfrak{s}$
. Let
![]() $r\in \mathfrak{s}$
such that
$r\in \mathfrak{s}$
such that
![]() $v(r-w)=\lambda _{\mathfrak{s}}$
. Then
$v(r-w)=\lambda _{\mathfrak{s}}$
. Then
Clearly
that implies
![]() $\rho _{\mathfrak{s}}=\lambda _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w)$
. Hence
$\rho _{\mathfrak{s}}=\lambda _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w)$
. Hence
![]() $w$
is a rational centre of
$w$
is a rational centre of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
On the other hand, suppose that all proper clusters
![]() $\mathfrak{s}\in \Sigma _f$
have rational centre
$\mathfrak{s}\in \Sigma _f$
have rational centre
![]() $w\in K$
and those with
$w\in K$
and those with
![]() $|\mathfrak{s}|\gt |\rho _{\mathfrak{s}}|_p$
satisfy
$|\mathfrak{s}|\gt |\rho _{\mathfrak{s}}|_p$
satisfy
![]() $d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
. Then
$d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
. Then
![]() $\rho _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w)$
for any
$\rho _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w)$
for any
![]() $\mathfrak{s}\in \Sigma _f$
. Thus
$\mathfrak{s}\in \Sigma _f$
. Thus
![]() $f_w$
is
$f_w$
is
![]() $\texttt{NP}$
-regular again by Theorem 3.24.
$\texttt{NP}$
-regular again by Theorem 3.24.
The next definition, which is the main (and only, if
![]() $p\neq 2$
) condition for our explicit construction of the minimal regular model of a hyperelliptic curve given by
$p\neq 2$
) condition for our explicit construction of the minimal regular model of a hyperelliptic curve given by
![]() $y^2=f(x)$
, follows from the statement of Corollary 3.25.
$y^2=f(x)$
, follows from the statement of Corollary 3.25.
Definition 3.26.
We say that
![]() $f$
has an almost rational cluster picture if all proper clusters
$f$
has an almost rational cluster picture if all proper clusters
![]() $\mathfrak{s}\in \Sigma _f$
with
$\mathfrak{s}\in \Sigma _f$
with
![]() $|\mathfrak{s}|\gt |\rho _{\mathfrak{s}}|_p$
have
$|\mathfrak{s}|\gt |\rho _{\mathfrak{s}}|_p$
have
![]() $d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
.
$d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
.
Corollary 3.25 shows that
![]() $f$
has a translation which is
$f$
has a translation which is
![]() $\texttt{NP}$
-regular if and only if
$\texttt{NP}$
-regular if and only if
![]() $f$
has an almost rational cluster picture and there exists
$f$
has an almost rational cluster picture and there exists
![]() $w\in K$
that is a rational centre of all clusters.
$w\in K$
that is a rational centre of all clusters.
In the following we give different characterisations of the previous definition.
Corollary 3.27.
Suppose that
![]() $K(\mathfrak{R})/K$
is a tamely ramified extension. Then
$K(\mathfrak{R})/K$
is a tamely ramified extension. Then
![]() $f$
has an almost rational cluster picture if and only if every proper cluster
$f$
has an almost rational cluster picture if and only if every proper cluster
![]() $\mathfrak{s}\in \Sigma _f$
is
$\mathfrak{s}\in \Sigma _f$
is
![]() $G_K$
-invariant.
$G_K$
-invariant.
Proof. Since
![]() $K(\mathfrak{R})/K$
is tamely ramified, every cluster
$K(\mathfrak{R})/K$
is tamely ramified, every cluster
![]() $\mathfrak{s}\in \Sigma _f$
has
$\mathfrak{s}\in \Sigma _f$
has
![]() $|\rho _{\mathfrak{s}}|_p\leq 1$
. Therefore, the Corollary follows from Remark 3.13.
$|\rho _{\mathfrak{s}}|_p\leq 1$
. Therefore, the Corollary follows from Remark 3.13.
Corollary 3.28.
Suppose that
![]() $K(\mathfrak{R})/K$
is a tamely ramified extension. Then
$K(\mathfrak{R})/K$
is a tamely ramified extension. Then
![]() $f_w$
is
$f_w$
is
![]() $\texttt{NP}$
-regular for some
$\texttt{NP}$
-regular for some
![]() $w\in K$
if and only if
$w\in K$
if and only if
![]() $\Sigma _f$
is nested.
$\Sigma _f$
is nested.
Proof. First note that every cluster
![]() $\mathfrak{s}\in \Sigma _f$
has
$\mathfrak{s}\in \Sigma _f$
has
![]() $|\rho _{\mathfrak{s}}|_p\leq 1$
, as
$|\rho _{\mathfrak{s}}|_p\leq 1$
, as
![]() $K(\mathfrak{R})/K$
is tamely ramified. Therefore, from Corollary 3.25, we need to prove that
$K(\mathfrak{R})/K$
is tamely ramified. Therefore, from Corollary 3.25, we need to prove that
![]() $\Sigma _f$
is nested if and only if all clusters
$\Sigma _f$
is nested if and only if all clusters
![]() $\mathfrak{s}\in \Sigma _f$
have
$\mathfrak{s}\in \Sigma _f$
have
![]() $d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
and rational centre
$d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
and rational centre
![]() $w$
, for some
$w$
, for some
![]() $w\in K$
. But this follows from Remark 3.13.
$w\in K$
. But this follows from Remark 3.13.
Corollary 3.29.
The polynomial
![]() $f$
has an almost rational cluster picture if and only if for every
$f$
has an almost rational cluster picture if and only if for every
![]() $r\in \mathfrak{R}\setminus K$
, there exists
$r\in \mathfrak{R}\setminus K$
, there exists
![]() $w\in K$
so that
$w\in K$
so that
![]() $r_w^b\;:\!=\;\frac{(r-w)^b}{\pi ^{b\cdot v(r-w)}}\mod \pi$
is a simple root of
$r_w^b\;:\!=\;\frac{(r-w)^b}{\pi ^{b\cdot v(r-w)}}\mod \pi$
is a simple root of
![]() $f_w|_L$
, where
$f_w|_L$
, where
![]() $b$
is the denominator of
$b$
is the denominator of
![]() $v(r-w)$
,
$v(r-w)$
,
![]() $f_w(x)=f(x+w)$
and
$f_w(x)=f(x+w)$
and
![]() $L$
is the edge of
$L$
is the edge of
![]() $\texttt{NP}(f_w)$
of slope
$\texttt{NP}(f_w)$
of slope
![]() $-v(r-w)$
.
$-v(r-w)$
.
Proof. Fix
![]() $\tilde{r}\in \mathfrak{R}\setminus K$
and let
$\tilde{r}\in \mathfrak{R}\setminus K$
and let
![]() $\mathfrak{s}$
be the smallest proper cluster containing
$\mathfrak{s}$
be the smallest proper cluster containing
![]() $\tilde{r}$
. Let
$\tilde{r}$
. Let
![]() $w_{\mathfrak{s}}$
be a rational centre of
$w_{\mathfrak{s}}$
be a rational centre of
![]() $\mathfrak{s}$
. Note that
$\mathfrak{s}$
. Note that
![]() $v(\tilde{r}-w_{\mathfrak{s}})=\rho _{\mathfrak{s}}=\min _{r\in \mathfrak{s}} v(r-w_{\mathfrak{s}})$
, for the choice of
$v(\tilde{r}-w_{\mathfrak{s}})=\rho _{\mathfrak{s}}=\min _{r\in \mathfrak{s}} v(r-w_{\mathfrak{s}})$
, for the choice of
![]() $\mathfrak{s}$
, as
$\mathfrak{s}$
, as
![]() $\tilde{r}\notin K$
. Moreover, for any proper cluster
$\tilde{r}\notin K$
. Moreover, for any proper cluster
![]() $\mathfrak{t}$
containing
$\mathfrak{t}$
containing
![]() $\tilde{r}$
, we have
$\tilde{r}$
, we have
![]() $\mathfrak{s}\subseteq \mathfrak{t}$
. In particular,
$\mathfrak{s}\subseteq \mathfrak{t}$
. In particular,
![]() $w_{\mathfrak{s}}$
is a rational centre of all such clusters. Let
$w_{\mathfrak{s}}$
is a rational centre of all such clusters. Let
![]() $L$
be the edge of
$L$
be the edge of
![]() $\texttt{NP}(f_{w_{\mathfrak{s}}})$
of slope
$\texttt{NP}(f_{w_{\mathfrak{s}}})$
of slope
![]() $-\rho _{\mathfrak{s}}$
. Theorem 3.24 shows that
$-\rho _{\mathfrak{s}}$
. Theorem 3.24 shows that
![]() $\tilde{r}_{w_{\mathfrak{s}}}^{b_{\mathfrak{s}}}$
is a multiple root of
$\tilde{r}_{w_{\mathfrak{s}}}^{b_{\mathfrak{s}}}$
is a multiple root of
![]() $f_{w_{\mathfrak{s}}}|_L$
if and only if there exists
$f_{w_{\mathfrak{s}}}|_L$
if and only if there exists
![]() $\mathfrak{t}\in \Sigma _f$
such that
$\mathfrak{t}\in \Sigma _f$
such that
![]() $\tilde{r}\in \mathfrak{t}$
,
$\tilde{r}\in \mathfrak{t}$
,
![]() $|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
and
$|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
and
![]() $d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}$
. Therefore, if
$d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}$
. Therefore, if
![]() $f$
has an almost rational cluster picture, then
$f$
has an almost rational cluster picture, then
![]() $\tilde{r}_{w_{\mathfrak{s}}}^{b_{\mathfrak{s}}}$
is a simple root.
$\tilde{r}_{w_{\mathfrak{s}}}^{b_{\mathfrak{s}}}$
is a simple root.
Suppose there exists
![]() $\mathfrak{t}\in \Sigma _f$
such that
$\mathfrak{t}\in \Sigma _f$
such that
![]() $|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
and
$|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
and
![]() $d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}$
. Then
$d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}$
. Then
![]() $\mathfrak{t}\cap K=\varnothing$
. By Theorem 3.24, it remains to show that for any
$\mathfrak{t}\cap K=\varnothing$
. By Theorem 3.24, it remains to show that for any
![]() $w\in K$
, we have
$w\in K$
, we have
![]() $|\mathfrak{t}|\gt |\lambda _{\mathfrak{t}}|_p$
and
$|\mathfrak{t}|\gt |\lambda _{\mathfrak{t}}|_p$
and
![]() $d_{\mathfrak{t}}\gt \lambda _{\mathfrak{t}}$
, where
$d_{\mathfrak{t}}\gt \lambda _{\mathfrak{t}}$
, where
![]() $\lambda _{\mathfrak{t}}=\min _{r\in \mathfrak{t}}v(r-w)$
. First note
$\lambda _{\mathfrak{t}}=\min _{r\in \mathfrak{t}}v(r-w)$
. First note
![]() $d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}\geq \lambda _{\mathfrak{t}}$
. Moreover, in the proof of Corollary 3.25, we saw that if
$d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}\geq \lambda _{\mathfrak{t}}$
. Moreover, in the proof of Corollary 3.25, we saw that if
![]() $|\mathfrak{t}|\leq |\lambda _{\mathfrak{t}}|_p$
then
$|\mathfrak{t}|\leq |\lambda _{\mathfrak{t}}|_p$
then
![]() $\rho _{\mathfrak{t}}=\lambda _{\mathfrak{t}}$
and so
$\rho _{\mathfrak{t}}=\lambda _{\mathfrak{t}}$
and so
![]() $|\mathfrak{t}|\leq |\rho _{\mathfrak{t}}|_p$
; but
$|\mathfrak{t}|\leq |\rho _{\mathfrak{t}}|_p$
; but
![]() $|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
, thus
$|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
, thus
![]() $|\mathfrak{t}|\gt |\lambda _{\mathfrak{t}}|_p$
.
$|\mathfrak{t}|\gt |\lambda _{\mathfrak{t}}|_p$
.
Lemma 3.30.
Suppose
![]() $f$
has an almost rational cluster picture. Let
$f$
has an almost rational cluster picture. Let
![]() $\mathfrak{s}\in \Sigma _f$
proper. If
$\mathfrak{s}\in \Sigma _f$
proper. If
![]() $d_{\mathfrak{s}}\gt \rho _{\mathfrak{s}}$
, then
$d_{\mathfrak{s}}\gt \rho _{\mathfrak{s}}$
, then
![]() $p\gt 0$
and
$p\gt 0$
and
![]() $|\mathfrak{s}|$
is a
$|\mathfrak{s}|$
is a
![]() $p$
-power. In particular, if
$p$
-power. In particular, if
![]() $w_{\mathfrak{s}}$
is a rational centre of
$w_{\mathfrak{s}}$
is a rational centre of
![]() $\mathfrak{s}$
, for any
$\mathfrak{s}$
, for any
![]() $r\in \mathfrak{s}$
, the elements
$r\in \mathfrak{s}$
, the elements
![]() $r-w_{\mathfrak{s}}$
are all the roots of a monic polynomial with coefficients in
$r-w_{\mathfrak{s}}$
are all the roots of a monic polynomial with coefficients in
![]() $K^{\textrm{s}}$
, and constant term
$K^{\textrm{s}}$
, and constant term
![]() $c$
such that
$c$
such that
![]() $|v(c)|_p\geq 1$
.
$|v(c)|_p\geq 1$
.
Proof. Let
![]() $\mathfrak{s}\in \Sigma _f$
proper, with
$\mathfrak{s}\in \Sigma _f$
proper, with
![]() $d_{\mathfrak{s}}\gt \rho _{\mathfrak{s}}$
. Since
$d_{\mathfrak{s}}\gt \rho _{\mathfrak{s}}$
. Since
![]() $f$
has an almost rational cluster picture, we must have
$f$
has an almost rational cluster picture, we must have
![]() $|\mathfrak{s}|\leq |\rho _{\mathfrak{s}}|_p$
. Since
$|\mathfrak{s}|\leq |\rho _{\mathfrak{s}}|_p$
. Since
![]() $\mathfrak{s}$
is proper,
$\mathfrak{s}$
is proper,
![]() $p\gt 0$
. Let
$p\gt 0$
. Let
![]() $b_{\mathfrak{s}}$
be the denominator of
$b_{\mathfrak{s}}$
be the denominator of
![]() $\rho _{\mathfrak{s}}$
. Then
$\rho _{\mathfrak{s}}$
. Then
![]() $v_p(b_{\mathfrak{s}})\gt 1$
. Fix a rational centre
$v_p(b_{\mathfrak{s}})\gt 1$
. Fix a rational centre
![]() $w_{\mathfrak{s}}$
of
$w_{\mathfrak{s}}$
of
![]() $\mathfrak{s}$
and a root
$\mathfrak{s}$
and a root
![]() $r\in \mathfrak{s}$
such that
$r\in \mathfrak{s}$
such that
![]() $v(r-w_{\mathfrak{s}})=\rho _{\mathfrak{s}}$
. Consider
$v(r-w_{\mathfrak{s}})=\rho _{\mathfrak{s}}$
. Consider
![]() $\mathfrak{s}^{\prime}=\{x\in \mathfrak{R}\mid v(x-r)\gt \rho _{\mathfrak{s}}\}$
. Then
$\mathfrak{s}^{\prime}=\{x\in \mathfrak{R}\mid v(x-r)\gt \rho _{\mathfrak{s}}\}$
. Then
![]() $\mathfrak{s}\subseteq \mathfrak{s}^{\prime}\leq{\mathfrak{s}}^{\textrm{rat}}$
and
$\mathfrak{s}\subseteq \mathfrak{s}^{\prime}\leq{\mathfrak{s}}^{\textrm{rat}}$
and
![]() $|\mathfrak{s}^{\prime}|\leq |\rho _{\mathfrak{s}}|_p$
(as
$|\mathfrak{s}^{\prime}|\leq |\rho _{\mathfrak{s}}|_p$
(as
![]() $d_{\mathfrak{s}^{\prime}}\gt \rho _{\mathfrak{s}}=\rho _{\mathfrak{s}^{\prime}}$
). Let
$d_{\mathfrak{s}^{\prime}}\gt \rho _{\mathfrak{s}}=\rho _{\mathfrak{s}^{\prime}}$
). Let
![]() $L$
be the Galois closure of
$L$
be the Galois closure of
![]() $K(r)$
. Let
$K(r)$
. Let
![]() $H$
be the wild inertia subgroup of
$H$
be the wild inertia subgroup of
![]() $\textrm{Gal}(L/K)$
and
$\textrm{Gal}(L/K)$
and
![]() $L^H$
the corresponding fixed field. Let
$L^H$
the corresponding fixed field. Let
![]() $\sigma _1,\dots,\sigma _n\in H$
such that
$\sigma _1,\dots,\sigma _n\in H$
such that
![]() $\sigma _1(r-w_{\mathfrak{s}}), \dots,\sigma _n(r-w_{\mathfrak{s}})$
are the roots of the minimal polynomial of
$\sigma _1(r-w_{\mathfrak{s}}), \dots,\sigma _n(r-w_{\mathfrak{s}})$
are the roots of the minimal polynomial of
![]() $r-w_{\mathfrak{s}}$
over
$r-w_{\mathfrak{s}}$
over
![]() $L^H$
. Hence
$L^H$
. Hence
![]() $\sigma _i(r)\in \mathfrak{R}$
and
$\sigma _i(r)\in \mathfrak{R}$
and
![]() $\sigma _i(r)\neq \sigma _j(r)$
for any
$\sigma _i(r)\neq \sigma _j(r)$
for any
![]() $i,j=1,\dots,n$
,
$i,j=1,\dots,n$
,
![]() $i\neq j$
. From
$i\neq j$
. From
it follows that
![]() $|\rho _{\mathfrak{s}}|_p\mid n$
, and so
$|\rho _{\mathfrak{s}}|_p\mid n$
, and so
![]() $|\rho _{\mathfrak{s}}|_p\leq n$
, since
$|\rho _{\mathfrak{s}}|_p\leq n$
, since
![]() $L^H/K$
is tamely ramified. By definition of
$L^H/K$
is tamely ramified. By definition of
![]() $H$
(see for example [Reference Neukirch17, Definition 9.3]) we have
$H$
(see for example [Reference Neukirch17, Definition 9.3]) we have
for any
![]() $i=1,\dots,n$
. Therefore
$i=1,\dots,n$
. Therefore
![]() $\sigma _i(r)\in \mathfrak{s}^{\prime}$
for all
$\sigma _i(r)\in \mathfrak{s}^{\prime}$
for all
![]() $i$
and so
$i$
and so
![]() $n\leq |\mathfrak{s}^{\prime}|$
. Thus
$n\leq |\mathfrak{s}^{\prime}|$
. Thus
![]() $n=|\mathfrak{s}^{\prime}|=|\rho _{\mathfrak{s}}|_p$
and
$n=|\mathfrak{s}^{\prime}|=|\rho _{\mathfrak{s}}|_p$
and
![]() $\mathfrak{s}\subseteq \mathfrak{s}^{\prime}=\{\sigma _i(r)\mid i=1,\dots,n\}$
. Finally, as
$\mathfrak{s}\subseteq \mathfrak{s}^{\prime}=\{\sigma _i(r)\mid i=1,\dots,n\}$
. Finally, as
![]() $\mathfrak{s}^{\prime}$
contains only conjugates of
$\mathfrak{s}^{\prime}$
contains only conjugates of
![]() $r\in \mathfrak{s}$
, the cluster
$r\in \mathfrak{s}$
, the cluster
![]() $\mathfrak{s}^{\prime}$
is union of orbits of
$\mathfrak{s}^{\prime}$
is union of orbits of
![]() $\mathfrak{s}$
. In particular,
$\mathfrak{s}$
. In particular,
![]() $|\mathfrak{s}|\mid |\mathfrak{s}^{\prime}|=|\rho _{\mathfrak{s}}|_p$
, and so
$|\mathfrak{s}|\mid |\mathfrak{s}^{\prime}|=|\rho _{\mathfrak{s}}|_p$
, and so
![]() $|\mathfrak{s}|$
is a
$|\mathfrak{s}|$
is a
![]() $p$
-power. The rest of the Lemma follows.
$p$
-power. The rest of the Lemma follows.
Proposition 3.31.
The polynomial
![]() $f$
has an almost rational cluster picture if and only if for every proper cluster
$f$
has an almost rational cluster picture if and only if for every proper cluster
![]() $\mathfrak{s}\in \Sigma _f$
one of the following is satisfied:
$\mathfrak{s}\in \Sigma _f$
one of the following is satisfied:
-
(a) the smallest disc containing
 $\mathfrak{s}$
also contains a rational point;
$\mathfrak{s}$
also contains a rational point;
-
(b)
 $p\gt 0$
and after a translation by an element of
$p\gt 0$
and after a translation by an element of
 $K$
, the elements in
$K$
, the elements in
 $\mathfrak{s}$
are all the roots of a monic polynomial with coefficients in
$\mathfrak{s}$
are all the roots of a monic polynomial with coefficients in
 $K^{\textrm{s}}$
of
$K^{\textrm{s}}$
of
 $p$
-power degree and constant term
$p$
-power degree and constant term
 $c$
such that
$c$
such that
 $|v(c)|_p\geq 1$
.
$|v(c)|_p\geq 1$
.
Proof. First of all, note that point (a) is equivalent to requiring
![]() $d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
. Therefore, by Lemma 3.30 it only remains to show that if
$d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
. Therefore, by Lemma 3.30 it only remains to show that if
![]() $\mathfrak{s}\in \Sigma _f$
with
$\mathfrak{s}\in \Sigma _f$
with
![]() $d_{\mathfrak{s}}\gt \rho _{\mathfrak{s}}$
and (b) is satisfied, then
$d_{\mathfrak{s}}\gt \rho _{\mathfrak{s}}$
and (b) is satisfied, then
![]() $|\mathfrak{s}|\leq |\rho _{\mathfrak{s}}|_p$
. Let
$|\mathfrak{s}|\leq |\rho _{\mathfrak{s}}|_p$
. Let
![]() $F\in K^{\textrm{s}}[x]$
be the polynomial in (b) and let
$F\in K^{\textrm{s}}[x]$
be the polynomial in (b) and let
![]() $w\in K$
such that
$w\in K$
such that
![]() $r-w$
, for
$r-w$
, for
![]() $r\in \mathfrak{s}$
, are all the roots of
$r\in \mathfrak{s}$
, are all the roots of
![]() $F$
. We have
$F$
. We have
![]() $\rho _{\mathfrak{s}}\geq \min _{r\in \mathfrak{s}}v(r-w)$
. Fix
$\rho _{\mathfrak{s}}\geq \min _{r\in \mathfrak{s}}v(r-w)$
. Fix
![]() $r\in \mathfrak{s}$
such that
$r\in \mathfrak{s}$
such that
![]() $\rho _{\mathfrak{s}}\geq v(r-w)\;=\!:\;\rho$
. Since
$\rho _{\mathfrak{s}}\geq v(r-w)\;=\!:\;\rho$
. Since
![]() $d_{\mathfrak{s}}\gt \rho _{\mathfrak{s}}\geq v(r-w)$
, we have
$d_{\mathfrak{s}}\gt \rho _{\mathfrak{s}}\geq v(r-w)$
, we have
![]() $v(r'-w)=v(r-w)=\rho$
for any
$v(r'-w)=v(r-w)=\rho$
for any
![]() $r'\in \mathfrak{s}$
. Then
$r'\in \mathfrak{s}$
. Then
We will prove that
![]() $\rho =\rho _{\mathfrak{s}}$
, so that
$\rho =\rho _{\mathfrak{s}}$
, so that
![]() $|\mathfrak{s}|\leq |\rho |_p=|\rho _{\mathfrak{s}}|_p$
, as required. We already know that
$|\mathfrak{s}|\leq |\rho |_p=|\rho _{\mathfrak{s}}|_p$
, as required. We already know that
![]() $\rho _{\mathfrak{s}}\geq \rho$
. Suppose by contradiction that
$\rho _{\mathfrak{s}}\geq \rho$
. Suppose by contradiction that
![]() $\rho _{\mathfrak{s}}\gt \rho$
. Let
$\rho _{\mathfrak{s}}\gt \rho$
. Let
![]() $w_{\mathfrak{s}}$
be a rational centre of
$w_{\mathfrak{s}}$
be a rational centre of
![]() $\mathfrak{s}$
and let
$\mathfrak{s}$
and let
![]() $r_{\mathfrak{s}}\in \mathfrak{s}$
such that
$r_{\mathfrak{s}}\in \mathfrak{s}$
such that
![]() $v(r_{\mathfrak{s}}-w_{\mathfrak{s}})=\rho _{\mathfrak{s}}$
. Hence
$v(r_{\mathfrak{s}}-w_{\mathfrak{s}})=\rho _{\mathfrak{s}}$
. Hence
But then
![]() $\rho \in \mathbb{Z}$
, which contradicts
$\rho \in \mathbb{Z}$
, which contradicts
![]() $|\mathfrak{s}|\leq |\rho |_p$
.
$|\mathfrak{s}|\leq |\rho |_p$
.
Example 3.32.
Let
![]() $p$
be a prime number and let
$p$
be a prime number and let
![]() $a\in \mathbb{Z}_p$
,
$a\in \mathbb{Z}_p$
,
![]() $b\in \mathbb{Z}_p^\times$
such that the polynomial
$b\in \mathbb{Z}_p^\times$
such that the polynomial
![]() $x^2+ax+b$
is not a square modulo
$x^2+ax+b$
is not a square modulo
![]() $p$
. Let
$p$
. Let
![]() $f\in \mathbb{Q}_p[x]$
given by
$f\in \mathbb{Q}_p[x]$
given by
![]() $f(x)=(x^6+ap^4x^3+bp^8)((x-p)^3-p^{11})$
. For any prime
$f(x)=(x^6+ap^4x^3+bp^8)((x-p)^3-p^{11})$
. For any prime
![]() $p$
the rational cluster picture of
$p$
the rational cluster picture of
![]() $f$
is
$f$
is

where
![]() $\rho _{\mathfrak{t}_3}=\frac{4}{3}$
,
$\rho _{\mathfrak{t}_3}=\frac{4}{3}$
,
![]() $\rho _{\mathfrak{t}_4}=\frac{11}{3}$
, and
$\rho _{\mathfrak{t}_4}=\frac{11}{3}$
, and
![]() $\rho _{\mathfrak{R}}=1$
.
$\rho _{\mathfrak{R}}=1$
.
If
![]() $p\neq 3$
, then the proper clusters of
$p\neq 3$
, then the proper clusters of
![]() $\Sigma _f$
coincide with the rational clusters above and
$\Sigma _f$
coincide with the rational clusters above and
![]() $d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
for any
$d_{\mathfrak{s}}=\rho _{\mathfrak{s}}$
for any
![]() $\mathfrak{s}=\mathfrak{t}_3,\mathfrak{t}_4,\mathfrak{R}$
. In particular,
$\mathfrak{s}=\mathfrak{t}_3,\mathfrak{t}_4,\mathfrak{R}$
. In particular,
![]() $f$
has an almost rational cluster picture when
$f$
has an almost rational cluster picture when
![]() $p\neq 3$
.
$p\neq 3$
.
Suppose
![]() $p=3$
. Then the cluster picture of
$p=3$
. Then the cluster picture of
![]() $f$
is
$f$
is

where
![]() $d_{\mathfrak{t}_1}=d_{\mathfrak{t}_2}=\frac{11}{6}$
,
$d_{\mathfrak{t}_1}=d_{\mathfrak{t}_2}=\frac{11}{6}$
,
![]() $d_{\mathfrak{t}_3}=\rho _{\mathfrak{t}_1}=\rho _{\mathfrak{t}_2}=\frac{4}{3}$
,
$d_{\mathfrak{t}_3}=\rho _{\mathfrak{t}_1}=\rho _{\mathfrak{t}_2}=\frac{4}{3}$
,
![]() $d_{\mathfrak{t}_4}=\frac{25}{6}$
and
$d_{\mathfrak{t}_4}=\frac{25}{6}$
and
![]() $d_{\mathfrak{R}}=1$
. Thus
$d_{\mathfrak{R}}=1$
. Thus
![]() $f$
has an almost rational cluster picture for all
$f$
has an almost rational cluster picture for all
![]() $p$
.
$p$
.
We conclude this section by showing that the cluster picture centred at
![]() $w\in K$
completely determines the Newton polygon of the translation of
$w\in K$
completely determines the Newton polygon of the translation of
![]() $f$
by
$f$
by
![]() $w$
.
$w$
.
Definition 3.33.
Let
![]() $z\in \bar{K}$
. A cluster centred at
$z\in \bar{K}$
. A cluster centred at
![]() $z$
is a cluster cut out by a
$z$
is a cluster cut out by a
![]() $v$
-adic disc of the form
$v$
-adic disc of the form
![]() $\mathcal{D}=\{x\in \bar{K}\mid v(x-z)\geq d\}$
for some
$\mathcal{D}=\{x\in \bar{K}\mid v(x-z)\geq d\}$
for some
![]() $d\in \mathbb{Q}$
.
$d\in \mathbb{Q}$
.
Definition 3.34.
Let
![]() $z\in \bar{K}$
. Define
$z\in \bar{K}$
. Define
![]() $\Sigma _f^z$
to be the set of all clusters centred at
$\Sigma _f^z$
to be the set of all clusters centred at
![]() $z$
. Write
$z$
. Write
![]() $\Sigma _f^z$
for the set
$\Sigma _f^z$
for the set
![]() $\Sigma _f^z\smallsetminus \{\{z\}\}$
. Note that
$\Sigma _f^z\smallsetminus \{\{z\}\}$
. Note that
![]() $\Sigma _f^z$
is nested, that is every cluster
$\Sigma _f^z$
is nested, that is every cluster
![]() $\mathfrak{s}\in \Sigma _f^z$
has at most one child in
$\mathfrak{s}\in \Sigma _f^z$
has at most one child in
![]() $\Sigma _f^z$
.
$\Sigma _f^z$
.
Definition 3.35.
Let
![]() $z\in \bar{K}$
, and let
$z\in \bar{K}$
, and let
![]() $\mathfrak{s}\in \Sigma _f\setminus \{\{z\}\}$
. The radius of
$\mathfrak{s}\in \Sigma _f\setminus \{\{z\}\}$
. The radius of
![]() $\mathfrak{s}$
with respect to the centre
$\mathfrak{s}$
with respect to the centre
![]() $z$
is
$z$
is
The cluster picture centred at
![]() $z$
of
$z$
of
![]() $f$
is the collection of all clusters in
$f$
is the collection of all clusters in
![]() $\Sigma _f^z$
together with their radii with respect to
$\Sigma _f^z$
together with their radii with respect to
![]() $z$
. Finally set
$z$
. Finally set
Remark 3.36.
From the definitions above, if
![]() $\mathfrak{s}$
is a cluster centred at
$\mathfrak{s}$
is a cluster centred at
![]() $z\in K^{\textrm{s}}$
, then
$z\in K^{\textrm{s}}$
, then
![]() $\mathfrak{s}=\mathfrak{R}\cap \{x\in \bar{K}\mid v(x-z)\geq \rho _{\mathfrak{s}}^z\}$
. But this does not mean
$\mathfrak{s}=\mathfrak{R}\cap \{x\in \bar{K}\mid v(x-z)\geq \rho _{\mathfrak{s}}^z\}$
. But this does not mean
![]() $z$
is a centre for
$z$
is a centre for
![]() $\mathfrak{s}$
, that is false in general. For example,
$\mathfrak{s}$
, that is false in general. For example,
![]() $\mathfrak{R}$
is clearly a cluster centred at any
$\mathfrak{R}$
is clearly a cluster centred at any
![]() $z\in K^{\textrm{s}}$
, but there are elements of
$z\in K^{\textrm{s}}$
, but there are elements of
![]() $K^{\textrm{s}}$
which are not centres of
$K^{\textrm{s}}$
which are not centres of
![]() $\mathfrak{R}$
, for example any
$\mathfrak{R}$
, for example any
![]() $z\in K^{\textrm{s}}$
with valuation
$z\in K^{\textrm{s}}$
with valuation
![]() $v(z)\lt \min _{r\in \mathfrak{R}}v(r)$
.
$v(z)\lt \min _{r\in \mathfrak{R}}v(r)$
.
Remark 3.37.
Let
![]() $\mathfrak{s}\in \Sigma _f$
be a proper cluster with centre
$\mathfrak{s}\in \Sigma _f$
be a proper cluster with centre
![]() $z$
and rational centre
$z$
and rational centre
![]() $w$
. Then
$w$
. Then
![]() $\mathfrak{s}\in \Sigma _f^{z}$
,
$\mathfrak{s}\in \Sigma _f^{z}$
,
![]() $d_{\mathfrak{s}}=\rho ^z_{\mathfrak{s}}$
,
$d_{\mathfrak{s}}=\rho ^z_{\mathfrak{s}}$
,
![]() $\nu _{\mathfrak{s}}=\epsilon ^z_{\mathfrak{s}}$
,
$\nu _{\mathfrak{s}}=\epsilon ^z_{\mathfrak{s}}$
,
![]() $\rho _{\mathfrak{s}}=\rho _{\mathfrak{s}}^w$
, and
$\rho _{\mathfrak{s}}=\rho _{\mathfrak{s}}^w$
, and
![]() $\epsilon _{\mathfrak{s}}=\epsilon _{\mathfrak{s}}^w$
. Furthermore,
$\epsilon _{\mathfrak{s}}=\epsilon _{\mathfrak{s}}^w$
. Furthermore,
![]() $\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
if and only if
$\mathfrak{s}\in \Sigma _f^{\textrm{rat}}$
if and only if
![]() $\mathfrak{s}\in \Sigma _f^{w}$
.
$\mathfrak{s}\in \Sigma _f^{w}$
.
The following result gives a complete description of the Newton polygon of the translation of
![]() $f$
by
$f$
by
![]() $w\in K$
, knowing the cluster picture centred at
$w\in K$
, knowing the cluster picture centred at
![]() $w$
of
$w$
of
![]() $f$
.
$f$
.
Lemma 3.38.
Let
![]() $w\in K$
and let
$w\in K$
and let
![]() $f_w(x)=f(x+w)$
. Then there is a
$f_w(x)=f(x+w)$
. Then there is a
![]() $1$
-to-
$1$
-to-
![]() $1$
correspondence between the clusters in
$1$
correspondence between the clusters in
![]() $\Sigma _f^w$
and the edges of
$\Sigma _f^w$
and the edges of
![]() $\texttt{NP}(f_w)$
. More explicitly, let
$\texttt{NP}(f_w)$
. More explicitly, let
![]() ${\mathfrak{s}}_1\subset \dots \subset{\mathfrak{s}}_n=\mathfrak{R}$
be the clusters in
${\mathfrak{s}}_1\subset \dots \subset{\mathfrak{s}}_n=\mathfrak{R}$
be the clusters in
![]() $\Sigma _f^w$
and let
$\Sigma _f^w$
and let
![]() ${\mathfrak{s}}_0=\{w\}$
if
${\mathfrak{s}}_0=\{w\}$
if
![]() $\{w\}\in \Sigma _f^w$
or
$\{w\}\in \Sigma _f^w$
or
![]() ${\mathfrak{s}}_0=\varnothing$
otherwise. Then
${\mathfrak{s}}_0=\varnothing$
otherwise. Then
![]() $\texttt{NP}(f_w)$
has vertices
$\texttt{NP}(f_w)$
has vertices
![]() $Q_i$
,
$Q_i$
,
![]() $i=0,\dots,n$
, where
$i=0,\dots,n$
, where
-
 $Q_n=(|\mathfrak{R}|,\epsilon _{\mathfrak{R}}^w-|\mathfrak{R}|\rho _{\mathfrak{R}}^w)=(\deg f,v(c_f))$
,
$Q_n=(|\mathfrak{R}|,\epsilon _{\mathfrak{R}}^w-|\mathfrak{R}|\rho _{\mathfrak{R}}^w)=(\deg f,v(c_f))$
, -
 $Q_i=(|{\mathfrak{s}}_i|,\epsilon _{{\mathfrak{s}}_i}^w-|{\mathfrak{s}}_i|\rho _{{\mathfrak{s}}_i}^w)=(|{\mathfrak{s}}_i|,\epsilon _{{\mathfrak{s}}_{i+1}}^w-|{\mathfrak{s}}_i|\rho _{{\mathfrak{s}}_{i+1}}^w)$
, for
$Q_i=(|{\mathfrak{s}}_i|,\epsilon _{{\mathfrak{s}}_i}^w-|{\mathfrak{s}}_i|\rho _{{\mathfrak{s}}_i}^w)=(|{\mathfrak{s}}_i|,\epsilon _{{\mathfrak{s}}_{i+1}}^w-|{\mathfrak{s}}_i|\rho _{{\mathfrak{s}}_{i+1}}^w)$
, for
 $i=1,\dots,n-1$
,
$i=1,\dots,n-1$
, -
 $Q_0=(|{\mathfrak{s}}_0|,\epsilon _{{\mathfrak{s}}_{1}}^w-|{\mathfrak{s}}_0|\rho _{{\mathfrak{s}}_{1}}^w)$
.
$Q_0=(|{\mathfrak{s}}_0|,\epsilon _{{\mathfrak{s}}_{1}}^w-|{\mathfrak{s}}_0|\rho _{{\mathfrak{s}}_{1}}^w)$
.
and edges
![]() $L_i$
,
$L_i$
,
![]() $i=1,\dots,n$
, of slope
$i=1,\dots,n$
, of slope
![]() $-\rho _{{\mathfrak{s}}_i}^w$
linking
$-\rho _{{\mathfrak{s}}_i}^w$
linking
![]() $Q_{i-1}$
and
$Q_{i-1}$
and
![]() $Q_i$
.
$Q_i$
.
Furthermore, for any
![]() $i=1,\dots,n$
we have
$i=1,\dots,n$
we have
where
![]() $\rho _i=\rho _{{\mathfrak{s}}_i}^w$
, and
$\rho _i=\rho _{{\mathfrak{s}}_i}^w$
, and
![]() $b_i$
is the denominator of
$b_i$
is the denominator of
![]() $\rho _i$
.
$\rho _i$
.
Proof. Without loss of generality we can assume
![]() $w=0$
so that
$w=0$
so that
![]() $f_w=f$
. First note that the coordinates of
$f_w=f$
. First note that the coordinates of
![]() $Q_n$
are trivial. Now consider a factorisation
$Q_n$
are trivial. Now consider a factorisation
![]() $f=c_f\cdot g_0\cdot g_1\cdots g_s$
of Theorem 2.2. Recall the polynomials
$f=c_f\cdot g_0\cdot g_1\cdots g_s$
of Theorem 2.2. Recall the polynomials
![]() $g_j$
are monic and
$g_j$
are monic and
![]() $g_0\mid x$
. Let
$g_0\mid x$
. Let
![]() $\mathfrak{R}_j$
be the set of roots of
$\mathfrak{R}_j$
be the set of roots of
![]() $g_j$
. It follows from the definition of cluster centred at
$g_j$
. It follows from the definition of cluster centred at
![]() $0$
that
$0$
that
Therefore
![]() ${\mathfrak{s}}_0=\mathfrak{R}_0$
and
${\mathfrak{s}}_0=\mathfrak{R}_0$
and
![]() $\mathfrak{R}_i={\mathfrak{s}}_i\setminus{\mathfrak{s}}_{i-1}$
for any
$\mathfrak{R}_i={\mathfrak{s}}_i\setminus{\mathfrak{s}}_{i-1}$
for any
![]() $i=1,\dots,n$
.
$i=1,\dots,n$
.
Let
![]() $i=1,\dots,n-1$
. Then the
$i=1,\dots,n-1$
. Then the
![]() $x$
-coordinate of
$x$
-coordinate of
![]() $Q_i$
follows as
$Q_i$
follows as
The
![]() $y$
-coordinate of
$y$
-coordinate of
![]() $Q_i$
equals the sum of
$Q_i$
equals the sum of
![]() $v(c_f)$
and the valuation of the constant term of
$v(c_f)$
and the valuation of the constant term of
![]() $\prod _{j=i+1}^n g_j$
, so
$\prod _{j=i+1}^n g_j$
, so
where
![]() $r_j$
is any root in
$r_j$
is any root in
![]() $\mathfrak{R}_j$
. But since
$\mathfrak{R}_j$
. But since
![]() ${\mathfrak{s}}_i=\bigcup _{j=0}^i\mathfrak{R}_j$
, we have
${\mathfrak{s}}_i=\bigcup _{j=0}^i\mathfrak{R}_j$
, we have
![]() $v(r_j)=\rho _{{\mathfrak{s}}_j}^0$
. Therefore
$v(r_j)=\rho _{{\mathfrak{s}}_j}^0$
. Therefore
Moreover,
from the easy computation
![]() $\epsilon _{{\mathfrak{s}}_i}^0-\epsilon _{{\mathfrak{s}}_{i+1}}^0=|{\mathfrak{s}}_i|\big (\rho _{{\mathfrak{s}}_i}^0-\rho _{{\mathfrak{s}}_{i+1}}^0\big ).$
Finally the
$\epsilon _{{\mathfrak{s}}_i}^0-\epsilon _{{\mathfrak{s}}_{i+1}}^0=|{\mathfrak{s}}_i|\big (\rho _{{\mathfrak{s}}_i}^0-\rho _{{\mathfrak{s}}_{i+1}}^0\big ).$
Finally the
![]() $x$
-coordinate of
$x$
-coordinate of
![]() $Q_0$
is trivial, while its
$Q_0$
is trivial, while its
![]() $y$
-coordinate equals
$y$
-coordinate equals
that concludes the first part of the proof as
![]() $|{\mathfrak{s}}_0|=|\mathfrak{R}_0|=\deg g_0$
.
$|{\mathfrak{s}}_0|=|\mathfrak{R}_0|=\deg g_0$
.
The computation of
![]() $f|_{L_i}$
follows from Remark 2.7. Indeed, let
$f|_{L_i}$
follows from Remark 2.7. Indeed, let
![]() $i=1,\dots,n$
, and define
$i=1,\dots,n$
, and define
![]() $\bar{c}_i=u/\pi ^{v(u)}\mod \pi$
, where
$\bar{c}_i=u/\pi ^{v(u)}\mod \pi$
, where
![]() $u=c_f\textstyle \prod _{j=i+1}^ng_j(0)$
. Then
$u=c_f\textstyle \prod _{j=i+1}^ng_j(0)$
. Then
![]() ${\overline{f|_{L_i}}}(x^{b_i})=\bar{c}_i\cdot{\overline{g_i|_{\texttt{NP}(g_i)}}}(x^{b_i})$
, where
${\overline{f|_{L_i}}}(x^{b_i})=\bar{c}_i\cdot{\overline{g_i|_{\texttt{NP}(g_i)}}}(x^{b_i})$
, where
![]() $b_i$
is the denominator of
$b_i$
is the denominator of
![]() $\rho _{{\mathfrak{s}}_i}^0$
. But
$\rho _{{\mathfrak{s}}_i}^0$
. But
Thus the Lemma follows as
![]() $\mathfrak{R}_i={\mathfrak{s}}_i\setminus{\mathfrak{s}}_{i-1}$
.
$\mathfrak{R}_i={\mathfrak{s}}_i\setminus{\mathfrak{s}}_{i-1}$
.
Notation 3.39.
Let
![]() $\mathfrak{s}\in \Sigma _f^w$
. Following the notation of Lemma 3.38, let
$\mathfrak{s}\in \Sigma _f^w$
. Following the notation of Lemma 3.38, let
![]() $i\in \{1,\dots,n\}$
be such that
$i\in \{1,\dots,n\}$
be such that
![]() $\mathfrak{s}={\mathfrak{s}}_i$
. We will write
$\mathfrak{s}={\mathfrak{s}}_i$
. We will write
![]() $L_{\mathfrak{s}}^w$
for the edge
$L_{\mathfrak{s}}^w$
for the edge
![]() $L_i$
.
$L_i$
.
4. Description of a regular model
From now on, assume
![]() $\textrm{char}(K)\neq 2$
and let
$\textrm{char}(K)\neq 2$
and let
![]() $C/K$
be a hyperelliptic curve, that is a geometrically connected, smooth, projective curve, equipped with a separable morphism
$C/K$
be a hyperelliptic curve, that is a geometrically connected, smooth, projective curve, equipped with a separable morphism
![]() $C\rightarrow{\mathbb{P}}^1_K$
of degree
$C\rightarrow{\mathbb{P}}^1_K$
of degree
![]() $2$
. Let
$2$
. Let
![]() $y^2=f(x)$
be a Weierstrass equation of
$y^2=f(x)$
be a Weierstrass equation of
![]() $C$
. Suppose
$C$
. Suppose
![]() $\deg f\gt 1$
. Let
$\deg f\gt 1$
. Let
![]() $g$
be the genus of
$g$
be the genus of
![]() $C$
. Accordingly with [Reference Dokchitser, Dokchitser, Maistret and Morgan14] we define the cluster picture of
$C$
. Accordingly with [Reference Dokchitser, Dokchitser, Maistret and Morgan14] we define the cluster picture of
![]() $C$
as the cluster picture of
$C$
as the cluster picture of
![]() $f$
. Analogously, all definitions and notations attached to
$f$
. Analogously, all definitions and notations attached to
![]() $f$
given in Section 3 (e.g.
$f$
given in Section 3 (e.g.
![]() $\Sigma _f$
,
$\Sigma _f$
,
![]() $\Sigma _f^{\textrm{rat}}$
,
$\Sigma _f^{\textrm{rat}}$
,
![]() $\Sigma _f^z$
) are given for
$\Sigma _f^z$
) are given for
![]() $C$
in the same way (e.g.
$C$
in the same way (e.g.
![]() $\Sigma _C$
,
$\Sigma _C$
,
![]() $\Sigma _C^{\textrm{rat}}$
,
$\Sigma _C^{\textrm{rat}}$
,
![]() $\Sigma _C^z$
). In particular, we will say that
$\Sigma _C^z$
). In particular, we will say that
![]() $C$
has an almost rational cluster picture if
$C$
has an almost rational cluster picture if
![]() $f$
does (Definition 3.26).
$f$
does (Definition 3.26).
For the following sections we will use the main definitions, notations and results of [Reference Dokchitser1, §
![]() $3$
]. In particular, we recall (without stating) the definitions of Newton polytopes
$3$
]. In particular, we recall (without stating) the definitions of Newton polytopes
![]() $\Delta$
and
$\Delta$
and
![]() $\Delta _v$
attached to a polynomial
$\Delta _v$
attached to a polynomial
![]() $g\in K[x,y]$
,
$g\in K[x,y]$
,
![]() $v$
-vertices/edges/faces of
$v$
-vertices/edges/faces of
![]() $\Delta$
, the denominator
$\Delta$
, the denominator
![]() $\delta _\lambda$
of a
$\delta _\lambda$
of a
![]() $v$
-face/edge
$v$
-face/edge
![]() $\lambda$
, the slopes
$\lambda$
, the slopes
![]() $s_1^\lambda, s_2^\lambda$
of a
$s_1^\lambda, s_2^\lambda$
of a
![]() $v$
-edge
$v$
-edge
![]() $\lambda$
.
$\lambda$
.
Notation 4.1.
We denote by
![]() $\Delta _v^w$
and
$\Delta _v^w$
and
![]() $\Delta ^w$
respectively the polytopes
$\Delta ^w$
respectively the polytopes
![]() $\Delta _v$
and
$\Delta _v$
and
![]() $\Delta$
attached to the polynomial
$\Delta$
attached to the polynomial
![]() $g_w(x,y)=y^2-f(x+w)$
. The piecewise affine function
$g_w(x,y)=y^2-f(x+w)$
. The piecewise affine function
![]() $v\;:\;\Delta ^w\rightarrow{\mathbb{R}}$
determining the bijection
$v\;:\;\Delta ^w\rightarrow{\mathbb{R}}$
determining the bijection
![]() $\Delta ^w\rightarrow \Delta _v^w$
,
$\Delta ^w\rightarrow \Delta _v^w$
,
![]() $P\mapsto (P,v(P))$
, will be denoted by
$P\mapsto (P,v(P))$
, will be denoted by
![]() $v$
(with a little abuse of notation). For a
$v$
(with a little abuse of notation). For a
![]() $v$
-face
$v$
-face
![]() $F$
of
$F$
of
![]() $\Delta ^w$
, denote by
$\Delta ^w$
, denote by
![]() $v_F\;:\;\Delta ^w\rightarrow{\mathbb{R}}$
the linear function equal to
$v_F\;:\;\Delta ^w\rightarrow{\mathbb{R}}$
the linear function equal to
![]() $v$
on
$v$
on
![]() $F$
. Since the projection
$F$
. Since the projection
![]() $\Delta _v^w\rightarrow \Delta ^w$
is a bijection, given a vertex/edge/face
$\Delta _v^w\rightarrow \Delta ^w$
is a bijection, given a vertex/edge/face
![]() $\lambda$
of
$\lambda$
of
![]() $\Delta _v^w$
we will denote by the same symbol
$\Delta _v^w$
we will denote by the same symbol
![]() $\lambda$
the corresponding
$\lambda$
the corresponding
![]() $v$
-vertex/edge/face of
$v$
-vertex/edge/face of
![]() $\Delta ^w$
. Since they are mainly used for indexing, this will not cause confusion.
$\Delta ^w$
. Since they are mainly used for indexing, this will not cause confusion.
Notation 4.2.
Given a
![]() $v$
-edge
$v$
-edge
![]() $\lambda$
of
$\lambda$
of
![]() $\Delta ^w$
, we will denote by
$\Delta ^w$
, we will denote by
![]() $r_\lambda$
the smallest non-negative integer such that we can fix
$r_\lambda$
the smallest non-negative integer such that we can fix
![]() $\frac{n_i}{d_i}\in \mathbb{Q}$
, for
$\frac{n_i}{d_i}\in \mathbb{Q}$
, for
![]() $i=0,\dots,r_\lambda +1$
so that
$i=0,\dots,r_\lambda +1$
so that
Thanks to Lemma 3.38 we can explicitly relate the Newton polytope
![]() $\Delta _v^w$
of
$\Delta _v^w$
of
![]() $g_w(x,y)$
and the cluster picture centred at
$g_w(x,y)$
and the cluster picture centred at
![]() $w$
of
$w$
of
![]() $C$
.
$C$
.
Lemma 4.3.
Let
![]() $w\in K$
. Then there is a
$w\in K$
. Then there is a
![]() $1$
-to-
$1$
-to-
![]() $1$
correspondence between the clusters in
$1$
correspondence between the clusters in
![]() $\Sigma _C^w$
and the faces of the Newton polytope
$\Sigma _C^w$
and the faces of the Newton polytope
![]() $\Delta _v^w$
. More explicitly, let
$\Delta _v^w$
. More explicitly, let
![]() ${\mathfrak{s}}_1\subset \dots \subset{\mathfrak{s}}_n=\mathfrak{R}$
be the clusters in
${\mathfrak{s}}_1\subset \dots \subset{\mathfrak{s}}_n=\mathfrak{R}$
be the clusters in
![]() $\Sigma _C^w$
and let
$\Sigma _C^w$
and let
![]() ${\mathfrak{s}}_0=\{w\}$
if
${\mathfrak{s}}_0=\{w\}$
if
![]() $\{w\}\in \Sigma _C^w$
or
$\{w\}\in \Sigma _C^w$
or
![]() ${\mathfrak{s}}_0=\varnothing$
otherwise. Then
${\mathfrak{s}}_0=\varnothing$
otherwise. Then
![]() $\Delta _v^w$
has vertices
$\Delta _v^w$
has vertices
![]() $T$
,
$T$
,
![]() $Q_i$
,
$Q_i$
,
![]() $i=0,\dots,n$
, where
$i=0,\dots,n$
, where
-
 $T=(0,2,0)$
,
$T=(0,2,0)$
, -
 $Q_n=(|\mathfrak{R}|,0,v(c_f))$
,
$Q_n=(|\mathfrak{R}|,0,v(c_f))$
, -
 $Q_i=(|{\mathfrak{s}}_i|,0,\epsilon _{{\mathfrak{s}}_{i+1}}^w-|{\mathfrak{s}}_i|\rho _{{\mathfrak{s}}_{i+1}}^w)$
for
$Q_i=(|{\mathfrak{s}}_i|,0,\epsilon _{{\mathfrak{s}}_{i+1}}^w-|{\mathfrak{s}}_i|\rho _{{\mathfrak{s}}_{i+1}}^w)$
for
 $i=0,\dots,n-1$
,
$i=0,\dots,n-1$
,
and edges
![]() $L_i$
(
$L_i$
(
![]() $i=1,\dots,n$
), linking
$i=1,\dots,n$
), linking
![]() $Q_{i-1}$
and
$Q_{i-1}$
and
![]() $Q_i$
, and
$Q_i$
, and
![]() $V_j$
(
$V_j$
(
![]() $j=0,\dots,n$
), linking
$j=0,\dots,n$
), linking
![]() $Q_j$
and
$Q_j$
and
![]() $T$
. Furthermore, (possible choices for) the slopes of the
$T$
. Furthermore, (possible choices for) the slopes of the
![]() $v$
-edges of
$v$
-edges of
![]() $\Delta ^w$
are:
$\Delta ^w$
are:
-
 \begin{align*} s_1^{V_n}=\delta _{V_n}\tfrac{-v(c_f)+(|\mathfrak{R}|-2g)\rho _{\mathfrak{R}}^w}{2}\quad \mbox{and}\quad s_2^{V_n}=\lfloor s_1^{V_n}-1\rfloor ; \end{align*}
\begin{align*} s_1^{V_n}=\delta _{V_n}\tfrac{-v(c_f)+(|\mathfrak{R}|-2g)\rho _{\mathfrak{R}}^w}{2}\quad \mbox{and}\quad s_2^{V_n}=\lfloor s_1^{V_n}-1\rfloor ; \end{align*}
-
 \begin{align*} \renewcommand{\arraystretch }{2} \begin{array}{l} s_1^{V_i}=\delta _{V_i}\left (-\frac{\epsilon _{{\mathfrak{s}}_{i}}^w}{2}+\left (\left \lfloor \frac{|{\mathfrak{s}}_i|}{2}\right \rfloor +1\right )\rho _{{\mathfrak{s}}_{i}}^w\right ),\\ s_2^{V_i}=\delta _{V_i}\left (-\frac{\epsilon _{{\mathfrak{s}}_{i+1}}^w}{2}+\left (\left \lfloor \frac{|{\mathfrak{s}}_i|}{2}\right \rfloor +1\right )\rho _{{\mathfrak{s}}_{i+1}}^w\right ) \end{array}\renewcommand{\arraystretch }{1} \quad \text{for all }i=1,\dots,n-1; \end{align*}
\begin{align*} \renewcommand{\arraystretch }{2} \begin{array}{l} s_1^{V_i}=\delta _{V_i}\left (-\frac{\epsilon _{{\mathfrak{s}}_{i}}^w}{2}+\left (\left \lfloor \frac{|{\mathfrak{s}}_i|}{2}\right \rfloor +1\right )\rho _{{\mathfrak{s}}_{i}}^w\right ),\\ s_2^{V_i}=\delta _{V_i}\left (-\frac{\epsilon _{{\mathfrak{s}}_{i+1}}^w}{2}+\left (\left \lfloor \frac{|{\mathfrak{s}}_i|}{2}\right \rfloor +1\right )\rho _{{\mathfrak{s}}_{i+1}}^w\right ) \end{array}\renewcommand{\arraystretch }{1} \quad \text{for all }i=1,\dots,n-1; \end{align*}
-
 \begin{align*} s_1^{V_0}=\delta _{V_0}\left (\tfrac{\epsilon _{{\mathfrak{s}}_1}^w}{2}-\rho _{{\mathfrak{s}}_1}^w\right )\quad \text{and}\quad s_2^{V_0}=\lfloor s_1^{V_0}-1\rfloor ; \end{align*}
\begin{align*} s_1^{V_0}=\delta _{V_0}\left (\tfrac{\epsilon _{{\mathfrak{s}}_1}^w}{2}-\rho _{{\mathfrak{s}}_1}^w\right )\quad \text{and}\quad s_2^{V_0}=\lfloor s_1^{V_0}-1\rfloor ; \end{align*}
-
 \begin{align*} s_1^{L_i}=\delta _{L_i}\left (-\tfrac{\epsilon _{{\mathfrak{s}}_{i}}^w}{2}+\left (\left \lfloor \tfrac{|{\mathfrak{s}}_i|}{2}\right \rfloor +1\right )\rho _{{\mathfrak{s}}_{i}}^w\right ) \quad \text{and}\quad s_2^{L_i}=\lfloor s_1^{L_i}-1\rfloor, \end{align*}
\begin{align*} s_1^{L_i}=\delta _{L_i}\left (-\tfrac{\epsilon _{{\mathfrak{s}}_{i}}^w}{2}+\left (\left \lfloor \tfrac{|{\mathfrak{s}}_i|}{2}\right \rfloor +1\right )\rho _{{\mathfrak{s}}_{i}}^w\right ) \quad \text{and}\quad s_2^{L_i}=\lfloor s_1^{L_i}-1\rfloor, \end{align*}
for all
 $i=1,\dots,n$
. In particular, as
$i=1,\dots,n$
. In particular, as
 $\delta _{L_i}$
is the denominator of
$\delta _{L_i}$
is the denominator of
 $\rho _{{\mathfrak{s}}_{i}}^w$
,
$\rho _{{\mathfrak{s}}_{i}}^w$
, \begin{align*} r_{L_i}=\begin{cases}1&\mbox{if }\delta _{L_i}\epsilon _{{\mathfrak{s}}_i}^w\mbox{ is odd,}\\0&\mbox{if }\delta _{L_i}\epsilon _{{\mathfrak{s}}_i}^w\mbox{ is even.}\end{cases} \end{align*}
\begin{align*} r_{L_i}=\begin{cases}1&\mbox{if }\delta _{L_i}\epsilon _{{\mathfrak{s}}_i}^w\mbox{ is odd,}\\0&\mbox{if }\delta _{L_i}\epsilon _{{\mathfrak{s}}_i}^w\mbox{ is even.}\end{cases} \end{align*}
Finally, for suitable choices of basis of the lattices in [ Reference Dokchitser1, 3.4, 3.5], we have
for any
![]() $i=1,\dots,n$
, where
$i=1,\dots,n$
, where
![]() $\rho _i=\rho _{{\mathfrak{s}}_i}^w$
, and
$\rho _i=\rho _{{\mathfrak{s}}_i}^w$
, and
![]() $b_i$
is the denominator of
$b_i$
is the denominator of
![]() $\rho _i$
;
$\rho _i$
;
for any
![]() $j=0,\dots,n$
, where
$j=0,\dots,n$
, where
![]() $|\bar{V}_j(\mathbb{Z})_{\mathbb{Z}}|$
is the number of integer points
$|\bar{V}_j(\mathbb{Z})_{\mathbb{Z}}|$
is the number of integer points
![]() $P$
on the
$P$
on the
![]() $v$
-edge
$v$
-edge
![]() $V_j$
with
$V_j$
with
![]() $v(P)\in \mathbb{Z}$
, endpoints included.
$v(P)\in \mathbb{Z}$
, endpoints included.
Proof. The structure of
![]() $\Delta _v^w$
follows from Lemma 3.38. For the computation of the slopes, we only need to individuate, for all the
$\Delta _v^w$
follows from Lemma 3.38. For the computation of the slopes, we only need to individuate, for all the
![]() $v$
-edges, the two points
$v$
-edges, the two points
![]() $P_0$
and
$P_0$
and
![]() $P_1$
of [Reference Dokchitser1, Definition 3.12]. It is easy to see that the followings are admissible choices.
$P_1$
of [Reference Dokchitser1, Definition 3.12]. It is easy to see that the followings are admissible choices.
-
For
 $V_i$
and
$V_i$
and
 $L_i$
(
$L_i$
(
 $i=1,\dots,n$
), choose
$i=1,\dots,n$
), choose
 $P_0=(|{\mathfrak{s}}_i|,0)$
and
$P_0=(|{\mathfrak{s}}_i|,0)$
and
 $P_1=\left (\left \lfloor \frac{|{\mathfrak{s}}_i|-1}{2}\right \rfloor,1\right )$
.
$P_1=\left (\left \lfloor \frac{|{\mathfrak{s}}_i|-1}{2}\right \rfloor,1\right )$
. -
For
 $V_0$
, choose
$V_0$
, choose
 $P_0=(0,2)$
and
$P_0=(0,2)$
and
 $P_1=(1,1)$
;
$P_1=(1,1)$
;
The second part of the Lemma then follows from the first one. The computations of the reductions also follows from Lemma 3.38 by choosing the lattices
![]() $Q_{i-1}+(b_i,0)\mathbb{Z}$
for
$Q_{i-1}+(b_i,0)\mathbb{Z}$
for
![]() $g_w|_{L_i}$
and
$g_w|_{L_i}$
and
![]() $Q_{i}+({-}|{\mathfrak{s}}_i|/a,2/a)\mathbb{Z}$
for
$Q_{i}+({-}|{\mathfrak{s}}_i|/a,2/a)\mathbb{Z}$
for
![]() $g_w|_{V_j}$
, where
$g_w|_{V_j}$
, where
![]() $a=|\bar{V}_j(\mathbb{Z})_{\mathbb{Z}}|-1$
.
$a=|\bar{V}_j(\mathbb{Z})_{\mathbb{Z}}|-1$
.
Notation 4.4.
Let
![]() $C$
be as above and let
$C$
be as above and let
![]() $w\in K$
. For every cluster
$w\in K$
. For every cluster
![]() $\mathfrak{s}\in \Sigma _C^w$
denote by
$\mathfrak{s}\in \Sigma _C^w$
denote by
![]() $F_{\mathfrak{s}}^w$
the
$F_{\mathfrak{s}}^w$
the
![]() $v$
-face of the Newton polytope
$v$
-face of the Newton polytope
![]() $\Delta ^w$
of
$\Delta ^w$
of
![]() $g_w(x,y)=y^2-f(x+w)$
that corresponds to
$g_w(x,y)=y^2-f(x+w)$
that corresponds to
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
Following the notation of Lemma 4.3, let
![]() $i\in \{1,\dots,n\}$
be such that
$i\in \{1,\dots,n\}$
be such that
![]() $\mathfrak{s}={\mathfrak{s}}_i$
. We will write
$\mathfrak{s}={\mathfrak{s}}_i$
. We will write
![]() $L_{\mathfrak{s}}^w$
,
$L_{\mathfrak{s}}^w$
,
![]() $V_{\mathfrak{s}}^w$
,
$V_{\mathfrak{s}}^w$
,
![]() $V_0^w$
for the
$V_0^w$
for the
![]() $v$
-edges
$v$
-edges
![]() $L_i$
,
$L_i$
,
![]() $V_i$
,
$V_i$
,
![]() $V_0$
, respectively.
$V_0$
, respectively.
Example 4.5.
Let
![]() $C$
be the hyperelliptic curve over
$C$
be the hyperelliptic curve over
![]() $\mathbb{Q}_3$
given by the equation
$\mathbb{Q}_3$
given by the equation
![]() $y^2=f(x)$
where
$y^2=f(x)$
where
![]() $f(x)=x^{11}-3x^6+9x^5-27$
is the polynomial of Example 3.20
.
$f(x)=x^{11}-3x^6+9x^5-27$
is the polynomial of Example 3.20
.
Its cluster picture centred at
![]() $0$
is
$0$
is

where the subscripts represent the radii with respect to
![]() $0$
. As we can see,
$0$
. As we can see,
![]() $\Sigma _C^0$
consists of two clusters:
$\Sigma _C^0$
consists of two clusters:
![]() ${\mathfrak{s}}_1$
of size
${\mathfrak{s}}_1$
of size
![]() $6$
, radius
$6$
, radius
![]() $\frac{1}{3}$
and
$\frac{1}{3}$
and
![]() $\epsilon _{{\mathfrak{s}}_1}^0=3$
, and
$\epsilon _{{\mathfrak{s}}_1}^0=3$
, and
![]() ${\mathfrak{s}}_2=\mathfrak{R}$
of size
${\mathfrak{s}}_2=\mathfrak{R}$
of size
![]() $11$
, radius
$11$
, radius
![]() $\frac{1}{5}$
and
$\frac{1}{5}$
and
![]() $\epsilon _{{\mathfrak{s}}_2}^0=\frac{11}{5}$
. Therefore the picture of
$\epsilon _{{\mathfrak{s}}_2}^0=\frac{11}{5}$
. Therefore the picture of
![]() $\Delta ^0$
broken into
$\Delta ^0$
broken into
![]() $v$
-faces will be
$v$
-faces will be

where
![]() $T=(0,2)$
,
$T=(0,2)$
,
![]() $Q_0=(0,0)$
,
$Q_0=(0,0)$
,
![]() $Q_1=(6,0)$
, and
$Q_1=(6,0)$
, and
![]() $Q_2=(11,0)$
. Denoting the values of
$Q_2=(11,0)$
. Denoting the values of
![]() $v$
on vertices, the picture becomes
$v$
on vertices, the picture becomes

To state the theorems which describe the special fibre of the proper flat model
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $C$
we will construct in Section 5, we need some definitions.
$C$
we will construct in Section 5, we need some definitions.
Definition 4.6.
Let
![]() $F/K$
be an unramified extension and let
$F/K$
be an unramified extension and let
![]() $\Sigma _F=\Sigma _{C_{F}}^{\textrm{rat}}$
(i.e. set of clusters cut out by discs with centre in
$\Sigma _F=\Sigma _{C_{F}}^{\textrm{rat}}$
(i.e. set of clusters cut out by discs with centre in
![]() $F$
). For any proper
$F$
). For any proper
![]() $\mathfrak{s}\in \Sigma _F$
let
$\mathfrak{s}\in \Sigma _F$
let
![]() $G_{\mathfrak{s}}=\textrm{Stab}_{G_K}(\mathfrak{s})$
and
$G_{\mathfrak{s}}=\textrm{Stab}_{G_K}(\mathfrak{s})$
and
![]() $K_{\mathfrak{s}}=\left ( K^{\textrm{s}}\right )^{G_{\mathfrak{s}}}$
. We define the following quantities:
$K_{\mathfrak{s}}=\left ( K^{\textrm{s}}\right )^{G_{\mathfrak{s}}}$
. We define the following quantities:
|
|
||
|---|---|---|
| radius |
|
|
|
|
denominator of
|
|
|
|
|
|
|
|
|
|
| multiplicity |
|
|
| parity |
|
|
| slope |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 if
|
|
Lemma 4.7.
Keep the notation of the previous definition and let
![]() $\mathfrak{s}\in \Sigma _K$
. Then
$\mathfrak{s}\in \Sigma _K$
. Then
![]() $\mathfrak{s}\in \Sigma _F$
but the quantities in Definition 4.6 do not depend on
$\mathfrak{s}\in \Sigma _F$
but the quantities in Definition 4.6 do not depend on
![]() $F$
.
$F$
.
Proof. A cluster
![]() $\mathfrak{s}\in \Sigma _F$
belongs to
$\mathfrak{s}\in \Sigma _F$
belongs to
![]() $\Sigma _K$
if and only if
$\Sigma _K$
if and only if
![]() $\sigma (\mathfrak{s})=\mathfrak{s}$
for any
$\sigma (\mathfrak{s})=\mathfrak{s}$
for any
![]() $\sigma \in G_K$
. Then the result follows from Lemma A.1.
$\sigma \in G_K$
. Then the result follows from Lemma A.1.
Remark 4.8.
Lemma 4.3 shed some light on the quantities we defined in Definition 4.6
. Let
![]() $\mathfrak{s}\in \Sigma _F$
. Fix a rational centre
$\mathfrak{s}\in \Sigma _F$
. Fix a rational centre
![]() $w_{\mathfrak{s}}\in F$
of
$w_{\mathfrak{s}}\in F$
of
![]() $\mathfrak{s}$
such that
$\mathfrak{s}$
such that
![]() $w_{\mathfrak{s}}\in K_{\mathfrak{s}}$
if
$w_{\mathfrak{s}}\in K_{\mathfrak{s}}$
if
![]() $p_{\mathfrak{s}}^0=1$
. Denoting
$p_{\mathfrak{s}}^0=1$
. Denoting
![]() $V=V_{\mathfrak{s}}^{w_{\mathfrak{s}}}$
,
$V=V_{\mathfrak{s}}^{w_{\mathfrak{s}}}$
,
![]() $L=L_{\mathfrak{s}}^{w_{\mathfrak{s}}}$
, and
$L=L_{\mathfrak{s}}^{w_{\mathfrak{s}}}$
, and
![]() $V_0=V_0^{w_{\mathfrak{s}}}$
, we have:
$V_0=V_0^{w_{\mathfrak{s}}}$
, we have:
-
 $b_{\mathfrak{s}}=\delta _L$
and
$b_{\mathfrak{s}}=\delta _L$
and
 $r_L=2-D_{\mathfrak{s}}$
.
$r_L=2-D_{\mathfrak{s}}$
. -
 $\gamma _{\mathfrak{s}}=\delta _V$
,
$\gamma _{\mathfrak{s}}=\delta _V$
,
 $p_{\mathfrak{s}}/\gamma _{\mathfrak{s}}=\bar{V}(\mathbb{Z})_{\mathbb{Z}}-1$
and
$p_{\mathfrak{s}}/\gamma _{\mathfrak{s}}=\bar{V}(\mathbb{Z})_{\mathbb{Z}}-1$
and
 $s_1^V=\gamma _{\mathfrak{s}} s_{\mathfrak{s}}$
. If
$s_1^V=\gamma _{\mathfrak{s}} s_{\mathfrak{s}}$
. If
 $V$
is internal, that is
$V$
is internal, that is
 $\mathfrak{s}\neq \mathfrak{R}$
, then
$\mathfrak{s}\neq \mathfrak{R}$
, then
 $s_2^V=\gamma _{\mathfrak{s}}(s_{\mathfrak{s}}-p_{\mathfrak{s}}\tfrac{\rho _{\mathfrak{s}}-\rho _{P(\mathfrak{s})}}{2})$
.
$s_2^V=\gamma _{\mathfrak{s}}(s_{\mathfrak{s}}-p_{\mathfrak{s}}\tfrac{\rho _{\mathfrak{s}}-\rho _{P(\mathfrak{s})}}{2})$
. -
If
 $\mathfrak{s}$
is minimal and so
$\mathfrak{s}$
is minimal and so
 $V_0$
is an edge of
$V_0$
is an edge of
 $F_{\mathfrak{s}}^{w_{\mathfrak{s}}}$
, then
$F_{\mathfrak{s}}^{w_{\mathfrak{s}}}$
, then
 $\gamma _{\mathfrak{s}}^0=\delta _{V_0}$
,
$\gamma _{\mathfrak{s}}^0=\delta _{V_0}$
,
 $p_{\mathfrak{s}}^0/\gamma _{\mathfrak{s}}^0=\bar{V}_0(\mathbb{Z})_{\mathbb{Z}}-1$
and
$p_{\mathfrak{s}}^0/\gamma _{\mathfrak{s}}^0=\bar{V}_0(\mathbb{Z})_{\mathbb{Z}}-1$
and
 $s_1^{V_0}=-\gamma _{\mathfrak{s}}^0 s_{\mathfrak{s}}^0$
.
$s_1^{V_0}=-\gamma _{\mathfrak{s}}^0 s_{\mathfrak{s}}^0$
.
Lemma 4.9.
Let
![]() $\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
with rational centre
$\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
with rational centre
![]() $w\in K$
. Then
$w\in K$
. Then
![]() $D_{\mathfrak{s}}=1$
if and only if
$D_{\mathfrak{s}}=1$
if and only if
![]() $v_{F_{\mathfrak{s}}^w}((a,1))\notin \mathbb{Z}$
, for every
$v_{F_{\mathfrak{s}}^w}((a,1))\notin \mathbb{Z}$
, for every
![]() $a\in \mathbb{Z}$
.
$a\in \mathbb{Z}$
.
Proof. If
![]() $D_{\mathfrak{s}}=1$
then
$D_{\mathfrak{s}}=1$
then
![]() $r_{L_{\mathfrak{s}}^w}=1$
by Lemma 4.3, and so
$r_{L_{\mathfrak{s}}^w}=1$
by Lemma 4.3, and so
![]() $v_{F_{\mathfrak{s}}^w}((a,1))\notin \mathbb{Z}$
, for every
$v_{F_{\mathfrak{s}}^w}((a,1))\notin \mathbb{Z}$
, for every
![]() $a\in \mathbb{Z}$
. Now let
$a\in \mathbb{Z}$
. Now let
![]() $c,d\in \mathbb{Z}$
such that
$c,d\in \mathbb{Z}$
such that
![]() $\rho _{\mathfrak{s}}\cdot c+d=1/b_{\mathfrak{s}}$
. If
$\rho _{\mathfrak{s}}\cdot c+d=1/b_{\mathfrak{s}}$
. If
![]() $D_{\mathfrak{s}}=2$
, then
$D_{\mathfrak{s}}=2$
, then
![]() $b_{\mathfrak{s}}\epsilon _{\mathfrak{s}}\in 2\mathbb{Z}$
, so
$b_{\mathfrak{s}}\epsilon _{\mathfrak{s}}\in 2\mathbb{Z}$
, so
as required.
Definition 4.10.
We say that
![]() $C$
is
$C$
is
![]() $y$
-regular if
$y$
-regular if
![]() $p\nmid D_{\mathfrak{s}}$
for every proper
$p\nmid D_{\mathfrak{s}}$
for every proper
![]() $\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
, that is if either
$\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
, that is if either
![]() $p\neq 2$
or
$p\neq 2$
or
![]() $D_{\mathfrak{s}}=1$
for any proper
$D_{\mathfrak{s}}=1$
for any proper
![]() $\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
.
$\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
.
Remark 4.11.
Let
![]() $F/K$
be an unramified extension. Then from Lemma 4.7
, if
$F/K$
be an unramified extension. Then from Lemma 4.7
, if
![]() $C_F$
is
$C_F$
is
![]() $y$
-regular then
$y$
-regular then
![]() $C$
is
$C$
is
![]() $y$
-regular.
$y$
-regular.
Lemma 4.12.
The hyperelliptic curve
![]() $C$
is
$C$
is
![]() $\Delta _v$
-regular if and only if
$\Delta _v$
-regular if and only if
![]() $C$
is
$C$
is
![]() $y$
-regular and
$y$
-regular and
![]() $f$
is
$f$
is
![]() $\texttt{NP}$
-regular.
$\texttt{NP}$
-regular.
Proof. Let
![]() $g(x,y)=y^2-f(x)$
. If
$g(x,y)=y^2-f(x)$
. If
![]() $C$
is
$C$
is
![]() $y$
-regular and
$y$
-regular and
![]() $f$
is
$f$
is
![]() $\texttt{NP}$
-regular, then
$\texttt{NP}$
-regular, then
![]() $C$
is
$C$
is
![]() $\Delta _v$
-regular by Lemma 4.3 and Lemma 4.9.
$\Delta _v$
-regular by Lemma 4.3 and Lemma 4.9.
Conversely, if
![]() $C$
is
$C$
is
![]() $\Delta _v$
-regular, then
$\Delta _v$
-regular, then
![]() $f$
is
$f$
is
![]() $\texttt{NP}$
-regular, and all clusters have rational centre
$\texttt{NP}$
-regular, and all clusters have rational centre
![]() $0$
by Corollary 3.25. It remains to show that if
$0$
by Corollary 3.25. It remains to show that if
![]() $p=2$
then
$p=2$
then
![]() $D_{\mathfrak{s}}=1$
for every proper
$D_{\mathfrak{s}}=1$
for every proper
![]() $\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
. Suppose there exists
$\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
. Suppose there exists
![]() $\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
such that
$\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
such that
![]() $D_{\mathfrak{s}}=2$
. Consider the variety
$D_{\mathfrak{s}}=2$
. Consider the variety
![]() $\bar{X}_{F_{\mathfrak{s}}^0}$
([Reference Dokchitser1, Definition 3.7]). By Lemma 4.9, the smoothness of
$\bar{X}_{F_{\mathfrak{s}}^0}$
([Reference Dokchitser1, Definition 3.7]). By Lemma 4.9, the smoothness of
![]() $\bar{X}_{F_{\mathfrak{s}}^0}$
implies there exists
$\bar{X}_{F_{\mathfrak{s}}^0}$
implies there exists
![]() $\mathfrak{s}^{\prime}\in \Sigma _C^{\textrm{rat}}$
, such that
$\mathfrak{s}^{\prime}\in \Sigma _C^{\textrm{rat}}$
, such that
![]() $|\mathfrak{s}|-|\mathfrak{s}^{\prime}|=1$
. Hence
$|\mathfrak{s}|-|\mathfrak{s}^{\prime}|=1$
. Hence
![]() $\rho _{\mathfrak{s}}\in \mathbb{Z}$
from Lemma 3.12. Therefore
$\rho _{\mathfrak{s}}\in \mathbb{Z}$
from Lemma 3.12. Therefore
![]() $\bar{F}_{\mathfrak{s}}^0(\mathbb{Z})=\bar{F}_{\mathfrak{s}}^0(\mathbb{Z})_{\mathbb{Z}}$
, by Lemma 4.9. But this gives a contradiction as it forces either
$\bar{F}_{\mathfrak{s}}^0(\mathbb{Z})=\bar{F}_{\mathfrak{s}}^0(\mathbb{Z})_{\mathbb{Z}}$
, by Lemma 4.9. But this gives a contradiction as it forces either
![]() $\overline{g|_{V_{\mathfrak{s}^{\prime}}^0}}$
or
$\overline{g|_{V_{\mathfrak{s}^{\prime}}^0}}$
or
![]() $\overline{g|_{V_{\mathfrak{s}}^0}}$
to be a square.
$\overline{g|_{V_{\mathfrak{s}}^0}}$
to be a square.
Definition 4.13.
Let
![]() $\mathfrak{s}\in \Sigma _F$
be a proper cluster and let
$\mathfrak{s}\in \Sigma _F$
be a proper cluster and let
![]() $c\in \{0,\dots,b_{\mathfrak{s}}-1\}$
such that
$c\in \{0,\dots,b_{\mathfrak{s}}-1\}$
such that
![]() $c\rho _{\mathfrak{s}}-\frac{1}{b_{\mathfrak{s}}}\in \mathbb{Z}$
. Define
$c\rho _{\mathfrak{s}}-\frac{1}{b_{\mathfrak{s}}}\in \mathbb{Z}$
. Define
where
![]() $\varnothing \lt \mathfrak{s}$
if
$\varnothing \lt \mathfrak{s}$
if
![]() $\mathfrak{s}$
is minimal and
$\mathfrak{s}$
is minimal and
![]() $p_{\mathfrak{s}}^0=2$
.
$p_{\mathfrak{s}}^0=2$
.
The genus
![]() $g(\mathfrak{s})$
of a rational cluster
$g(\mathfrak{s})$
of a rational cluster
![]() $\mathfrak{s}\in \Sigma _F$
is defined as follows:
$\mathfrak{s}\in \Sigma _F$
is defined as follows:
-
If
 $D_{\mathfrak{s}}=1$
, then
$D_{\mathfrak{s}}=1$
, then
 $g(\mathfrak{s})=0$
.
$g(\mathfrak{s})=0$
. -
If
 $D_{\mathfrak{s}}=2$
, then
$D_{\mathfrak{s}}=2$
, then
 $2g(\mathfrak{s})+1$
or
$2g(\mathfrak{s})+1$
or
 $2g(\mathfrak{s})+2$
equals
$2g(\mathfrak{s})+2$
equals
 \begin{align*} \frac{|\mathfrak{s}|-\sum _{\mathfrak{s}^{\prime}\in \Sigma _F,\mathfrak{s}^{\prime}\lt \mathfrak{s}}|\mathfrak{s}^{\prime}|}{b_{\mathfrak{s}}}+|\tilde{\mathfrak{s}}|. \end{align*}
\begin{align*} \frac{|\mathfrak{s}|-\sum _{\mathfrak{s}^{\prime}\in \Sigma _F,\mathfrak{s}^{\prime}\lt \mathfrak{s}}|\mathfrak{s}^{\prime}|}{b_{\mathfrak{s}}}+|\tilde{\mathfrak{s}}|. \end{align*}
Definition 4.14.
Let
![]() $\Sigma _C^{\textrm{min}}$
be the set of rationally minimal clusters of
$\Sigma _C^{\textrm{min}}$
be the set of rationally minimal clusters of
![]() $C$
and let
$C$
and let
![]() $\Sigma \subseteq \Sigma _C^{\textrm{min}}$
non-empty. For each cluster
$\Sigma \subseteq \Sigma _C^{\textrm{min}}$
non-empty. For each cluster
![]() $\mathfrak{s}\in \Sigma$
, fix a rational centre
$\mathfrak{s}\in \Sigma$
, fix a rational centre
![]() $w_{\mathfrak{s}}$
; if possible, choose
$w_{\mathfrak{s}}$
; if possible, choose
![]() $w_{\mathfrak{s}}\in \mathfrak{s}$
. Let
$w_{\mathfrak{s}}\in \mathfrak{s}$
. Let
![]() $W$
be the set of these rational centres and define
$W$
be the set of these rational centres and define
![]() $\Sigma ^W=\bigcup _{w\in W}\Sigma _C^w$
. For any proper cluster
$\Sigma ^W=\bigcup _{w\in W}\Sigma _C^w$
. For any proper cluster
![]() $\mathfrak{s}\in \Sigma ^W$
fix a rational centre
$\mathfrak{s}\in \Sigma ^W$
fix a rational centre
![]() $w_{\mathfrak{s}}\in W$
. Denote
$w_{\mathfrak{s}}\in W$
. Denote
![]() $r_{\mathfrak{s}}=\frac{w_{\mathfrak{s}}-r}{\pi ^{\rho _{\mathfrak{s}}}}$
for
$r_{\mathfrak{s}}=\frac{w_{\mathfrak{s}}-r}{\pi ^{\rho _{\mathfrak{s}}}}$
for
![]() $r\in \mathfrak{R}$
. Define reductions
$r\in \mathfrak{R}$
. Define reductions
![]() $\overline{f_{\mathfrak{s}}^W}(x)\in k[x]$
,
$\overline{f_{\mathfrak{s}}^W}(x)\in k[x]$
,
![]() $\overline{g_{\mathfrak{s}}}\in k[y]$
, and for
$\overline{g_{\mathfrak{s}}}\in k[y]$
, and for
![]() $\mathfrak{s}\in \Sigma$
also
$\mathfrak{s}\in \Sigma$
also
![]() $\overline{g_{\mathfrak{s}}^0}\in k[y]$
by
$\overline{g_{\mathfrak{s}}^0}\in k[y]$
by
 \begin{align*} \overline{f_{\mathfrak{s}}^W}(x^{b_{\mathfrak{s}}})&= \tfrac{u}{\pi ^{v(u)}}\prod _{r\in \mathfrak{s}\setminus \bigcup _{\mathfrak{s}^{\prime}\lt \mathfrak{s}}\mathfrak{s}^{\prime}} (x+r_{\mathfrak{s}})\mod \pi,& u&=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \mathfrak{s}} r_{\mathfrak{s}},\\ \overline{g_{\mathfrak{s}}}(y) &= y^{p_{\mathfrak{s}}/\gamma _{\mathfrak{s}}} - \tfrac{u}{\pi ^{v(u)}}\mod \pi, & u&=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \mathfrak{s}} r_{\mathfrak{s}},\\ \overline{g_{\mathfrak{s}}^0}(y) &= y^{p_{\mathfrak{s}}^0/\gamma _{\mathfrak{s}}^0} - \tfrac{u}{\pi ^{v(u)}}\mod \pi, & u&=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \{w_{\mathfrak{s}}\}} r_{\mathfrak{s}}. \end{align*}
\begin{align*} \overline{f_{\mathfrak{s}}^W}(x^{b_{\mathfrak{s}}})&= \tfrac{u}{\pi ^{v(u)}}\prod _{r\in \mathfrak{s}\setminus \bigcup _{\mathfrak{s}^{\prime}\lt \mathfrak{s}}\mathfrak{s}^{\prime}} (x+r_{\mathfrak{s}})\mod \pi,& u&=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \mathfrak{s}} r_{\mathfrak{s}},\\ \overline{g_{\mathfrak{s}}}(y) &= y^{p_{\mathfrak{s}}/\gamma _{\mathfrak{s}}} - \tfrac{u}{\pi ^{v(u)}}\mod \pi, & u&=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \mathfrak{s}} r_{\mathfrak{s}},\\ \overline{g_{\mathfrak{s}}^0}(y) &= y^{p_{\mathfrak{s}}^0/\gamma _{\mathfrak{s}}^0} - \tfrac{u}{\pi ^{v(u)}}\mod \pi, & u&=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \{w_{\mathfrak{s}}\}} r_{\mathfrak{s}}. \end{align*}
where the union runs through all
![]() $\mathfrak{s}^{\prime}\in \Sigma ^W$
,
$\mathfrak{s}^{\prime}\in \Sigma ^W$
,
![]() $\mathfrak{s}^{\prime}\lt \mathfrak{s}$
. Finally define the
$\mathfrak{s}^{\prime}\lt \mathfrak{s}$
. Finally define the
![]() $k$
-schemes
$k$
-schemes
-
(1)
 $ X_{\mathfrak{s}}^W\;:\;\{{\overline{f_{\mathfrak{s}}^W}}=0\}\subset{\mathbb{G}}_{m,k}$
;
$ X_{\mathfrak{s}}^W\;:\;\{{\overline{f_{\mathfrak{s}}^W}}=0\}\subset{\mathbb{G}}_{m,k}$
; -
(2)
 $ X_{\mathfrak{s}}\;:\;\{{\overline{g_{\mathfrak{s}}}}=0\}\subset{\mathbb{G}}_{m,k}$
;
$ X_{\mathfrak{s}}\;:\;\{{\overline{g_{\mathfrak{s}}}}=0\}\subset{\mathbb{G}}_{m,k}$
; -
(3)
 $ X_{\mathfrak{s}}^0\;:\;\{{\overline{g_{\mathfrak{s}}^0}}=0\}\subset{\mathbb{G}}_{m,k}$
if
$ X_{\mathfrak{s}}^0\;:\;\{{\overline{g_{\mathfrak{s}}^0}}=0\}\subset{\mathbb{G}}_{m,k}$
if
 $\mathfrak{s}\in \Sigma$
.
$\mathfrak{s}\in \Sigma$
.
Notation 4.15.
Given a scheme
![]() $\mathcal{X}/O_K$
we will denote by
$\mathcal{X}/O_K$
we will denote by
![]() $\mathcal{X}_\eta$
its generic fibre
$\mathcal{X}_\eta$
its generic fibre
![]() $\mathcal{X}\times _{\textrm{Spec}\, O_K}\textrm{Spec}\, K$
, and by
$\mathcal{X}\times _{\textrm{Spec}\, O_K}\textrm{Spec}\, K$
, and by
![]() $\mathcal{X}_s$
its special fibre
$\mathcal{X}_s$
its special fibre
![]() $\mathcal{X}\times _{\textrm{Spec}\, O_K}\textrm{Spec}\, k$
.
$\mathcal{X}\times _{\textrm{Spec}\, O_K}\textrm{Spec}\, k$
.
Notation 4.16.
If
![]() $C=C_1\cup \dots \cup C_r$
is a chain of
$C=C_1\cup \dots \cup C_r$
is a chain of
![]() ${\mathbb{P}}^1_k$
s of length
${\mathbb{P}}^1_k$
s of length
![]() $r$
and multiplicities
$r$
and multiplicities
![]() $m_i\in \mathbb{Z}$
(meeting transversely), then
$m_i\in \mathbb{Z}$
(meeting transversely), then
![]() $\infty \in C_i$
is identified with
$\infty \in C_i$
is identified with
![]() $0\in C_{i+1}$
, and
$0\in C_{i+1}$
, and
![]() $0,\infty \in C$
are respectively
$0,\infty \in C$
are respectively
![]() $0\in C_{1}$
and
$0\in C_{1}$
and
![]() $\infty \in C_{r}$
. Finally, if
$\infty \in C_{r}$
. Finally, if
![]() $r=0$
, then
$r=0$
, then
![]() $C=\textrm{Spec}\, k$
and
$C=\textrm{Spec}\, k$
and
![]() $0=\infty$
.
$0=\infty$
.
Notation 4.17.
Let
![]() $\alpha \in \mathbb{Z}_+$
,
$\alpha \in \mathbb{Z}_+$
,
![]() $a,b\in \mathbb{Q}$
, with
$a,b\in \mathbb{Q}$
, with
![]() $a\gt b$
, and fix
$a\gt b$
, and fix
![]() $\frac{n_i}{d_i}\in \mathbb{Q}$
so that
$\frac{n_i}{d_i}\in \mathbb{Q}$
so that
and
![]() $r$
minimal. We write
$r$
minimal. We write
![]() ${\mathbb{P}}^1(\alpha,a,b)$
for a chain of
${\mathbb{P}}^1(\alpha,a,b)$
for a chain of
![]() ${\mathbb{P}}^1_k$
s of length
${\mathbb{P}}^1_k$
s of length
![]() $r$
and multiplicities
$r$
and multiplicities
![]() $\alpha d_1,\dots,\alpha d_r$
. Furthermore, we denote by
$\alpha d_1,\dots,\alpha d_r$
. Furthermore, we denote by
![]() ${\mathbb{P}}^1(\alpha,a)$
the chain
${\mathbb{P}}^1(\alpha,a)$
the chain
![]() ${\mathbb{P}}^1(\alpha,a,\lfloor \alpha a-1\rfloor/\alpha )$
.
${\mathbb{P}}^1(\alpha,a,\lfloor \alpha a-1\rfloor/\alpha )$
.
Theorem 4.18 and Theorem 4.23 will follow from Section 5.
Theorem 4.18.
Let
![]() $C/K$
be a hyperelliptic curve given by a Weierstrass equation
$C/K$
be a hyperelliptic curve given by a Weierstrass equation
![]() $y^2=f(x)$
. Suppose
$y^2=f(x)$
. Suppose
![]() $\deg f\gt 1$
and let
$\deg f\gt 1$
and let
![]() $\Sigma$
,
$\Sigma$
,
![]() $W$
and
$W$
and
![]() $\Sigma ^W$
as in Definition 4.14
. Then there exists a proper flat model
$\Sigma ^W$
as in Definition 4.14
. Then there exists a proper flat model
![]() $\mathcal{C}/O_K$
(constructed in Section 5
) of
$\mathcal{C}/O_K$
(constructed in Section 5
) of
![]() $C$
such that its special fibre
$C$
such that its special fibre
![]() $\mathcal{C}_s/k$
consists of
$\mathcal{C}_s/k$
consists of
![]() $1$
-dimensional schemes given below in (1), (2), (3), (4), (5), glued along
$1$
-dimensional schemes given below in (1), (2), (3), (4), (5), glued along
![]() $0$
-dimensional transversal intersections:
$0$
-dimensional transversal intersections:
-
(1) Every proper cluster
 $\mathfrak{s}\in \Sigma ^W$
gives a
$\mathfrak{s}\in \Sigma ^W$
gives a
 $1$
-dimensional closed subscheme
$1$
-dimensional closed subscheme
 $\Gamma _{\mathfrak{s}}$
of multiplicity
$\Gamma _{\mathfrak{s}}$
of multiplicity
 $m_{\mathfrak{s}}$
.
$m_{\mathfrak{s}}$
.
 $\Gamma _{\mathfrak{s}}$
is not integral if and only if
$\Gamma _{\mathfrak{s}}$
is not integral if and only if
 $D_{\mathfrak{s}}=2$
,
$D_{\mathfrak{s}}=2$
,
 $\tilde{\mathfrak{s}}\cap (\Sigma ^W\cup \{\varnothing \})=\varnothing$
and
$\tilde{\mathfrak{s}}\cap (\Sigma ^W\cup \{\varnothing \})=\varnothing$
and
 $\overline{f_{\mathfrak{s}}^W}$
is a square. When this happens, if
$\overline{f_{\mathfrak{s}}^W}$
is a square. When this happens, if
 $p=2$
then
$p=2$
then
 $\Gamma _{\mathfrak{s}}$
is not reduced and
$\Gamma _{\mathfrak{s}}$
is not reduced and
 $(\Gamma _{\mathfrak{s}})_{\textrm{red}}$
is irreducible of multiplicity
$(\Gamma _{\mathfrak{s}})_{\textrm{red}}$
is irreducible of multiplicity
 $2$
in
$2$
in
 $\Gamma _{\mathfrak{s}}$
, if
$\Gamma _{\mathfrak{s}}$
, if
 $p\neq 2$
then
$p\neq 2$
then
 $\Gamma _{\mathfrak{s}}$
is reducible, namely
$\Gamma _{\mathfrak{s}}$
is reducible, namely
 $\Gamma _{\mathfrak{s}}=\Gamma _{\mathfrak{s}}^+\cup \Gamma _{\mathfrak{s}}^-$
, with
$\Gamma _{\mathfrak{s}}=\Gamma _{\mathfrak{s}}^+\cup \Gamma _{\mathfrak{s}}^-$
, with
 $\Gamma _{\mathfrak{s}}^{\pm }={\mathbb{P}}^1_k$
.
$\Gamma _{\mathfrak{s}}^{\pm }={\mathbb{P}}^1_k$
. -
(2) Every proper cluster
 $\mathfrak{s}\in \Sigma ^W$
with
$\mathfrak{s}\in \Sigma ^W$
with
 $D_{\mathfrak{s}}=1$
gives the closed subscheme
$D_{\mathfrak{s}}=1$
gives the closed subscheme
 $X_{\mathfrak{s}}^W\times{\mathbb{P}}^1_k$
, of multiplicity
$X_{\mathfrak{s}}^W\times{\mathbb{P}}^1_k$
, of multiplicity
 $b_{\mathfrak{s}}$
, where
$b_{\mathfrak{s}}$
, where
 $X_{\mathfrak{s}}^W\times \{0\}\subset \Gamma _{\mathfrak{s}}$
.
$X_{\mathfrak{s}}^W\times \{0\}\subset \Gamma _{\mathfrak{s}}$
. -
(3) Every proper cluster
 $\mathfrak{s}\in \Sigma ^W$
such that
$\mathfrak{s}\in \Sigma ^W$
such that
 $\mathfrak{s}\neq \mathfrak{R}$
, gives the closed subscheme
$\mathfrak{s}\neq \mathfrak{R}$
, gives the closed subscheme
 $X_{\mathfrak{s}}\times{\mathbb{P}}^1(\gamma _{\mathfrak{s}},s_{\mathfrak{s}},s_{\mathfrak{s}}-p_{\mathfrak{s}}\cdot \frac{\rho _{\mathfrak{s}}-\rho _{P(\mathfrak{s})}}{2})$
where
$X_{\mathfrak{s}}\times{\mathbb{P}}^1(\gamma _{\mathfrak{s}},s_{\mathfrak{s}},s_{\mathfrak{s}}-p_{\mathfrak{s}}\cdot \frac{\rho _{\mathfrak{s}}-\rho _{P(\mathfrak{s})}}{2})$
where
 $X_{\mathfrak{s}}\times \{0\}\subset \Gamma _{\mathfrak{s}}$
and
$X_{\mathfrak{s}}\times \{0\}\subset \Gamma _{\mathfrak{s}}$
and
 $X_{\mathfrak{s}}\times \{\infty \}\subset \Gamma _{P(\mathfrak{s})}$
.
$X_{\mathfrak{s}}\times \{\infty \}\subset \Gamma _{P(\mathfrak{s})}$
. -
(4) Every cluster
 $\mathfrak{s}\in \Sigma$
gives the closed subscheme
$\mathfrak{s}\in \Sigma$
gives the closed subscheme
 $X_{\mathfrak{s}}^0\times{\mathbb{P}}^1(\gamma _{\mathfrak{s}}^0,-s_{\mathfrak{s}}^0)$
where
$X_{\mathfrak{s}}^0\times{\mathbb{P}}^1(\gamma _{\mathfrak{s}}^0,-s_{\mathfrak{s}}^0)$
where
 $X_{\mathfrak{s}}^0\times \{0\}\subset \Gamma _{\mathfrak{s}}$
(the chains are open-ended).
$X_{\mathfrak{s}}^0\times \{0\}\subset \Gamma _{\mathfrak{s}}$
(the chains are open-ended).
-
(5) Finally, the cluster
 $\mathfrak{R}$
gives the closed subscheme
$\mathfrak{R}$
gives the closed subscheme
 $X_{\mathfrak{R}}\times{\mathbb{P}}^1(\gamma _{\mathfrak{R}},s_{\mathfrak{R}})$
where
$X_{\mathfrak{R}}\times{\mathbb{P}}^1(\gamma _{\mathfrak{R}},s_{\mathfrak{R}})$
where
 $X_{\mathfrak{R}}\times \{0\}\subset \Gamma _{\mathfrak{R}}$
(the chains are open-ended).
$X_{\mathfrak{R}}\times \{0\}\subset \Gamma _{\mathfrak{R}}$
(the chains are open-ended).
If
![]() $\Gamma _{\mathfrak{s}}$
is reducible, the two points in
$\Gamma _{\mathfrak{s}}$
is reducible, the two points in
![]() $X_{\mathfrak{s}}\times \{0\}$
(and
$X_{\mathfrak{s}}\times \{0\}$
(and
![]() $X_{\mathfrak{s}}^0\times \{0\}$
if
$X_{\mathfrak{s}}^0\times \{0\}$
if
![]() $\mathfrak{s}\in \Sigma$
) belong to different irreducible components of
$\mathfrak{s}\in \Sigma$
) belong to different irreducible components of
![]() $\Gamma _{\mathfrak{s}}$
. Similarly, if
$\Gamma _{\mathfrak{s}}$
. Similarly, if
![]() $\mathfrak{s}\neq \mathfrak{R}$
and
$\mathfrak{s}\neq \mathfrak{R}$
and
![]() $\Gamma _{P(\mathfrak{s})}$
is reducible, the two points of
$\Gamma _{P(\mathfrak{s})}$
is reducible, the two points of
![]() $X_{\mathfrak{s}}\times \{\infty \}$
belong to different irreducible components of
$X_{\mathfrak{s}}\times \{\infty \}$
belong to different irreducible components of
![]() $\Gamma _{P(\mathfrak{s})}$
.
$\Gamma _{P(\mathfrak{s})}$
.
Furthermore, if
![]() $C$
has an almost rational cluster picture and is
$C$
has an almost rational cluster picture and is
![]() $y$
-regular, then, by choosing
$y$
-regular, then, by choosing
![]() $\Sigma =\Sigma _C^{\textrm{min}}$
, the model
$\Sigma =\Sigma _C^{\textrm{min}}$
, the model
![]() $\mathcal{C}$
is regular with strict normal crossings. In that case, if
$\mathcal{C}$
is regular with strict normal crossings. In that case, if
![]() $\mathfrak{s}$
is übereven and
$\mathfrak{s}$
is übereven and
![]() $\epsilon _{\mathfrak{s}}$
is even, then
$\epsilon _{\mathfrak{s}}$
is even, then
![]() $\Gamma _{\mathfrak{s}}\simeq X_{\mathfrak{s}}\times{\mathbb{P}}^1_k$
, otherwise
$\Gamma _{\mathfrak{s}}\simeq X_{\mathfrak{s}}\times{\mathbb{P}}^1_k$
, otherwise
![]() $\Gamma _{\mathfrak{s}}$
is irreducible of genus
$\Gamma _{\mathfrak{s}}$
is irreducible of genus
![]() $g(\mathfrak{s})$
.
$g(\mathfrak{s})$
.
Remark 4.19.
Consider the proper flat model
![]() $\mathcal{C}/O_K$
of Theorem 4.18. Via the canonical immersion
$\mathcal{C}/O_K$
of Theorem 4.18. Via the canonical immersion
![]() $\mathcal{C}_s\hookrightarrow \mathcal{C}$
, the singular points of
$\mathcal{C}_s\hookrightarrow \mathcal{C}$
, the singular points of
![]() $\mathcal{C}$
are images of
$\mathcal{C}$
are images of
-
singular points of the subscheme given in (1) when
 $D_{\mathfrak{s}}=2$
and either
$D_{\mathfrak{s}}=2$
and either
 $p=2$
, or
$p=2$
, or
 $\mathfrak{s}=\mathfrak{t}^{\textrm{rat}}$
for some
$\mathfrak{s}=\mathfrak{t}^{\textrm{rat}}$
for some
 $\mathfrak{t}\in \Sigma _C$
with
$\mathfrak{t}\in \Sigma _C$
with
 $|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
and
$|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
and
 $d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}$
, or
$d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}$
, or
 $\mathfrak{s}={\mathfrak{s}}_1\wedge{\mathfrak{s}}_2$
for some
$\mathfrak{s}={\mathfrak{s}}_1\wedge{\mathfrak{s}}_2$
for some
 ${\mathfrak{s}}_1\in \Sigma$
and
${\mathfrak{s}}_1\in \Sigma$
and
 ${\mathfrak{s}}_2\in \Sigma _C^{\textrm{min}}\smallsetminus \Sigma$
;
${\mathfrak{s}}_2\in \Sigma _C^{\textrm{min}}\smallsetminus \Sigma$
; -
non-reduced points of the subscheme given in (2) when
 $D_{\mathfrak{s}}=1$
and either
$D_{\mathfrak{s}}=1$
and either
 $\mathfrak{s}=\mathfrak{t}^{\textrm{rat}}$
for some
$\mathfrak{s}=\mathfrak{t}^{\textrm{rat}}$
for some
 $\mathfrak{t}\in \Sigma _C$
with
$\mathfrak{t}\in \Sigma _C$
with
 $|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
and
$|\mathfrak{t}|\gt |\rho _{\mathfrak{t}}|_p$
and
 $d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}$
, or
$d_{\mathfrak{t}}\gt \rho _{\mathfrak{t}}$
, or
 $\mathfrak{s}={\mathfrak{s}}_1\wedge{\mathfrak{s}}_2$
for some
$\mathfrak{s}={\mathfrak{s}}_1\wedge{\mathfrak{s}}_2$
for some
 ${\mathfrak{s}}_1\in \Sigma$
and
${\mathfrak{s}}_1\in \Sigma$
and
 ${\mathfrak{s}}_2\in \Sigma _C^{\textrm{min}}\smallsetminus \Sigma$
;
${\mathfrak{s}}_2\in \Sigma _C^{\textrm{min}}\smallsetminus \Sigma$
; -
non-reduced points of subschemes given in (3), (4), (5) (that may exist only if
 $p=2$
).
$p=2$
).
Note that
![]() $\mathcal{C}$
is not necessarily normal, hence it may have infinitely many singular points.
$\mathcal{C}$
is not necessarily normal, hence it may have infinitely many singular points.
Definition 4.20.
Let
![]() $\mathfrak{s}\in \Sigma _{K^{nr}}$
. We say that
$\mathfrak{s}\in \Sigma _{K^{nr}}$
. We say that
-
 $\mathfrak{s}$
is removable if either
$\mathfrak{s}$
is removable if either
 $|\mathfrak{s}|=1$
, or
$|\mathfrak{s}|=1$
, or
 $\mathfrak{s}$
has a child
$\mathfrak{s}$
has a child
 $\mathfrak{s}^{\prime}\in \Sigma _{K^{nr}}$
of size
$\mathfrak{s}^{\prime}\in \Sigma _{K^{nr}}$
of size
 $2g+1$
(
$2g+1$
(
 $\mathfrak{s}=\mathfrak{R}$
in this case).
$\mathfrak{s}=\mathfrak{R}$
in this case).
-
 $\mathfrak{s}$
is contractible if
$\mathfrak{s}$
is contractible if
-
(1)
 $|\mathfrak{s}|=2$
and
$|\mathfrak{s}|=2$
and
 $\rho _{\mathfrak{s}}\notin \mathbb{Z}$
,
$\rho _{\mathfrak{s}}\notin \mathbb{Z}$
,
 $\epsilon _{\mathfrak{s}}$
odd,
$\epsilon _{\mathfrak{s}}$
odd,
 $\rho _{P(\mathfrak{s})}\leq \rho _{\mathfrak{s}}-\frac{1}{2};$
or
$\rho _{P(\mathfrak{s})}\leq \rho _{\mathfrak{s}}-\frac{1}{2};$
or
-
(2)
 $\mathfrak{s}=\mathfrak{R}$
of size
$\mathfrak{s}=\mathfrak{R}$
of size
 $2g+2$
, with a child
$2g+2$
, with a child
 $\mathfrak{s}^{\prime}\in \Sigma _{K^{nr}}$
of size
$\mathfrak{s}^{\prime}\in \Sigma _{K^{nr}}$
of size
 $2g$
, and
$2g$
, and
 $\rho _{\mathfrak{s}}\notin \mathbb{Z}$
,
$\rho _{\mathfrak{s}}\notin \mathbb{Z}$
,
 $v(c_f)$
odd,
$v(c_f)$
odd,
 $\rho _{\mathfrak{s}^{\prime}}\geq \rho _{\mathfrak{s}}+\frac{1}{2}$
; or
$\rho _{\mathfrak{s}^{\prime}}\geq \rho _{\mathfrak{s}}+\frac{1}{2}$
; or
-
(3)
 $\mathfrak{s}=\mathfrak{R}$
of size
$\mathfrak{s}=\mathfrak{R}$
of size
 $2g+2$
, union of its
$2g+2$
, union of its
 $2$
odd proper children
$2$
odd proper children
 ${\mathfrak{s}}_1,{\mathfrak{s}}_2\in \Sigma _{K^{nr}}$
, with
${\mathfrak{s}}_1,{\mathfrak{s}}_2\in \Sigma _{K^{nr}}$
, with
 $v(c_f)$
odd,
$v(c_f)$
odd,
 $\rho _{{\mathfrak{s}}_i}\geq \rho _{\mathfrak{s}}+1$
for
$\rho _{{\mathfrak{s}}_i}\geq \rho _{\mathfrak{s}}+1$
for
 $i=1,2$
.
$i=1,2$
.
-
Notation 4.21.
Write
![]() $\Sigma ^{nr}\subseteq \Sigma _{K^{nr}}$
for the subset of non-removable clusters.
$\Sigma ^{nr}\subseteq \Sigma _{K^{nr}}$
for the subset of non-removable clusters.
Definition 4.22.
Choose rational centres
![]() $w_{\mathfrak{s}}\in K^{nr}$
for every
$w_{\mathfrak{s}}\in K^{nr}$
for every
![]() $\mathfrak{s}\in \Sigma ^{nr}$
, in such a way that
$\mathfrak{s}\in \Sigma ^{nr}$
, in such a way that
![]() $w_{\mathfrak{s}}\in \mathfrak{s}$
when
$w_{\mathfrak{s}}\in \mathfrak{s}$
when
![]() $p_{\mathfrak{s}}^0=1$
, and
$p_{\mathfrak{s}}^0=1$
, and
![]() $\sigma (w_{\mathfrak{s}})=w_{\sigma (\mathfrak{s})}$
for all
$\sigma (w_{\mathfrak{s}})=w_{\sigma (\mathfrak{s})}$
for all
![]() $\sigma \in \textrm{Gal}(K^{nr}/K)$
. Denote
$\sigma \in \textrm{Gal}(K^{nr}/K)$
. Denote
![]() $r_{\mathfrak{s}}=\frac{w_{\mathfrak{s}}-r}{\pi ^{\rho _{\mathfrak{s}}}}$
for
$r_{\mathfrak{s}}=\frac{w_{\mathfrak{s}}-r}{\pi ^{\rho _{\mathfrak{s}}}}$
for
![]() $r\in \mathfrak{R}$
and define
$r\in \mathfrak{R}$
and define
![]() $\overline{g_{\mathfrak{s}}}, \overline{g_{\mathfrak{s}}^0}\in k^{\textrm{s}}[y]$
as in Definition 4.14, and
$\overline{g_{\mathfrak{s}}}, \overline{g_{\mathfrak{s}}^0}\in k^{\textrm{s}}[y]$
as in Definition 4.14, and
![]() $\overline{f_{\mathfrak{s}}}(x)\in k^{\textrm{s}}[x]$
, by
$\overline{f_{\mathfrak{s}}}(x)\in k^{\textrm{s}}[x]$
, by
where the union runs through all
![]() $\mathfrak{s}^{\prime}\in \Sigma ^{nr}$
,
$\mathfrak{s}^{\prime}\in \Sigma ^{nr}$
,
![]() $\mathfrak{s}^{\prime}\lt \mathfrak{s}$
. Let
$\mathfrak{s}^{\prime}\lt \mathfrak{s}$
. Let
![]() $G_{\mathfrak{s}}=\textrm{Stab}_{G_K}(\mathfrak{s})$
,
$G_{\mathfrak{s}}=\textrm{Stab}_{G_K}(\mathfrak{s})$
,
![]() $K_{\mathfrak{s}}=\left ( K^{\textrm{s}}\right )^{G_{\mathfrak{s}}}$
, and let
$K_{\mathfrak{s}}=\left ( K^{\textrm{s}}\right )^{G_{\mathfrak{s}}}$
, and let
![]() $k_{\mathfrak{s}}$
be the residue field of
$k_{\mathfrak{s}}$
be the residue field of
![]() $K_{\mathfrak{s}}$
. Then
$K_{\mathfrak{s}}$
. Then
![]() ${\overline{f_{\mathfrak{s}}}}\in k_{\mathfrak{s}}[x]$
,
${\overline{f_{\mathfrak{s}}}}\in k_{\mathfrak{s}}[x]$
,
![]() ${\overline{g_{\mathfrak{s}}}}\in k_{\mathfrak{s}}[y]$
, and for
${\overline{g_{\mathfrak{s}}}}\in k_{\mathfrak{s}}[y]$
, and for
![]() $\mathfrak{s}$
minimal
$\mathfrak{s}$
minimal
![]() ${\overline{g_{\mathfrak{s}}^0}}\in k_{\mathfrak{s}}[y]$
.
${\overline{g_{\mathfrak{s}}^0}}\in k_{\mathfrak{s}}[y]$
.
Let
![]() ${\mathfrak{s}}_0\in \Sigma ^{nr}$
be minimal and contained in
${\mathfrak{s}}_0\in \Sigma ^{nr}$
be minimal and contained in
![]() $\mathfrak{s}$
. Denote
$\mathfrak{s}$
. Denote
![]() $\mathfrak{s}=\tilde{\mathfrak{s}}\setminus \{\{r\}\lt \mathfrak{s}\mid r\neq w_{{\mathfrak{s}}_0}\}$
. Note that
$\mathfrak{s}=\tilde{\mathfrak{s}}\setminus \{\{r\}\lt \mathfrak{s}\mid r\neq w_{{\mathfrak{s}}_0}\}$
. Note that
![]() $\mathfrak{s}$
does not depend on the choice of
$\mathfrak{s}$
does not depend on the choice of
![]() ${\mathfrak{s}}_0$
. Define
${\mathfrak{s}}_0$
. Define
![]() $\tilde{f_{\mathfrak{s}}}\in k_{\mathfrak{s}}[x]$
by
$\tilde{f_{\mathfrak{s}}}\in k_{\mathfrak{s}}[x]$
by
where
![]() ${\overline{u_{\mathfrak{s}^{\prime},\mathfrak{s}}}}=\frac{w_{\mathfrak{s}^{\prime}}-w_{\mathfrak{s}}}{\pi ^{\rho _{\mathfrak{s}}}}\mod \pi$
if
${\overline{u_{\mathfrak{s}^{\prime},\mathfrak{s}}}}=\frac{w_{\mathfrak{s}^{\prime}}-w_{\mathfrak{s}}}{\pi ^{\rho _{\mathfrak{s}}}}\mod \pi$
if
![]() $\mathfrak{s}^{\prime}\neq \varnothing$
and
$\mathfrak{s}^{\prime}\neq \varnothing$
and
![]() ${\overline{u_{\mathfrak{s}^{\prime},\mathfrak{s}}}}=0$
otherwise.
${\overline{u_{\mathfrak{s}^{\prime},\mathfrak{s}}}}=0$
otherwise.
In the next theorem we describe the special fibre of the minimal regular model of
![]() $C$
with normal crossings. We use Definitions/Notations 3.1, 3.3, 3.4, 3.2, 3.8, 3.9, 3.26, 4.6, 4.10, 4.13, 4.17, 4.20, 4.21, 4.22 in the statement. Note that a full description of the model is developed in Section 5.
$C$
with normal crossings. We use Definitions/Notations 3.1, 3.3, 3.4, 3.2, 3.8, 3.9, 3.26, 4.6, 4.10, 4.13, 4.17, 4.20, 4.21, 4.22 in the statement. Note that a full description of the model is developed in Section 5.
Theorem 4.23 (Minimal regular NC model). Let
![]() $C/K\; : \;y^2=f(x)$
be a hyperelliptic curve of genus
$C/K\; : \;y^2=f(x)$
be a hyperelliptic curve of genus
![]() $\geq 1$
. Suppose
$\geq 1$
. Suppose
![]() $C_{K^{nr}}$
has an almost rational cluster picture and is
$C_{K^{nr}}$
has an almost rational cluster picture and is
![]() $y$
-regular. Then the minimal regular model with normal crossings
$y$
-regular. Then the minimal regular model with normal crossings
![]() $\mathcal{C}^{\textrm{min}}/O_{K^{nr}}$
of
$\mathcal{C}^{\textrm{min}}/O_{K^{nr}}$
of
![]() $C$
has special fibre
$C$
has special fibre
![]() $\mathcal{C}_s^{\textrm{min}}/k^{\textrm{s}}$
described as follows:
$\mathcal{C}_s^{\textrm{min}}/k^{\textrm{s}}$
described as follows:
-
(1) Every
 $\mathfrak{s}\in \Sigma ^{nr}$
gives a
$\mathfrak{s}\in \Sigma ^{nr}$
gives a
 $1$
-dimensional subscheme
$1$
-dimensional subscheme
 $\Gamma _{\mathfrak{s}}$
of multiplicity
$\Gamma _{\mathfrak{s}}$
of multiplicity
 $m_{\mathfrak{s}}$
. If
$m_{\mathfrak{s}}$
. If
 $\mathfrak{s}$
is übereven and
$\mathfrak{s}$
is übereven and
 $\epsilon _{\mathfrak{s}}$
is even, then
$\epsilon _{\mathfrak{s}}$
is even, then
 $\Gamma _{\mathfrak{s}}$
is the disjoint union of
$\Gamma _{\mathfrak{s}}$
is the disjoint union of
 $\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}\simeq{\mathbb{P}}^1$
and
$\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}\simeq{\mathbb{P}}^1$
and
 $\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}\simeq{\mathbb{P}}^1$
, otherwise
$\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}\simeq{\mathbb{P}}^1$
, otherwise
 $\Gamma _{\mathfrak{s}}$
is irreducible of genus
$\Gamma _{\mathfrak{s}}$
is irreducible of genus
 $g(\mathfrak{s})$
(write
$g(\mathfrak{s})$
(write
 $\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}=\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}=\Gamma _{\mathfrak{s}}$
in this case). The indices
$\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}=\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}=\Gamma _{\mathfrak{s}}$
in this case). The indices
 $r_{\mathfrak{s},-}$
and
$r_{\mathfrak{s},-}$
and
 $r_{\mathfrak{s},+}$
are the roots of
$r_{\mathfrak{s},+}$
are the roots of
 $\overline{g_{\mathfrak{s}}}$
(where
$\overline{g_{\mathfrak{s}}}$
(where
 $r_{\mathfrak{s},-}=r_{\mathfrak{s},+}$
if
$r_{\mathfrak{s},-}=r_{\mathfrak{s},+}$
if
 $\deg{\overline{g_{\mathfrak{s}}}}=1$
).
$\deg{\overline{g_{\mathfrak{s}}}}=1$
).
-
(2) Every
 $\mathfrak{s}\in \Sigma ^{nr}$
with
$\mathfrak{s}\in \Sigma ^{nr}$
with
 $D_{\mathfrak{s}}=1$
gives open-ended
$D_{\mathfrak{s}}=1$
gives open-ended
 ${\mathbb{P}}^1$
s of multiplicity
${\mathbb{P}}^1$
s of multiplicity
 $b_{\mathfrak{s}}$
from
$b_{\mathfrak{s}}$
from
 $\Gamma _{\mathfrak{s}}$
indexed by roots of
$\Gamma _{\mathfrak{s}}$
indexed by roots of
 $\overline{f_{\mathfrak{s}}}$
.
$\overline{f_{\mathfrak{s}}}$
. -
(3) Every non-maximal element
 $\mathfrak{s}\in \Sigma ^{nr}$
gives chains
$\mathfrak{s}\in \Sigma ^{nr}$
gives chains
 ${\mathbb{P}}^1(\gamma _{\mathfrak{s}},s_{\mathfrak{s}},s_{\mathfrak{s}}-p_{\mathfrak{s}}\cdot \frac{\rho _{\mathfrak{s}}-\rho _{P(\mathfrak{s})}}{2})$
from
${\mathbb{P}}^1(\gamma _{\mathfrak{s}},s_{\mathfrak{s}},s_{\mathfrak{s}}-p_{\mathfrak{s}}\cdot \frac{\rho _{\mathfrak{s}}-\rho _{P(\mathfrak{s})}}{2})$
from
 $\Gamma _{\mathfrak{s}}$
to
$\Gamma _{\mathfrak{s}}$
to
 $\Gamma _{P(\mathfrak{s})}$
indexed by roots of
$\Gamma _{P(\mathfrak{s})}$
indexed by roots of
 $\overline{g_{\mathfrak{s}}}$
.
$\overline{g_{\mathfrak{s}}}$
. -
(4) Every minimal element
 $\mathfrak{s}\in \Sigma ^{nr}$
gives open-ended chains
$\mathfrak{s}\in \Sigma ^{nr}$
gives open-ended chains
 ${\mathbb{P}}^1(\gamma _{\mathfrak{s}}^0,-s_{\mathfrak{s}}^0)$
from
${\mathbb{P}}^1(\gamma _{\mathfrak{s}}^0,-s_{\mathfrak{s}}^0)$
from
 $\Gamma _{\mathfrak{s}}$
indexed by roots of
$\Gamma _{\mathfrak{s}}$
indexed by roots of
 $\overline{g_{\mathfrak{s}}^0}$
.
$\overline{g_{\mathfrak{s}}^0}$
. -
(5) The maximal element
 $\mathfrak{s}\in \Sigma ^{nr}$
gives open-ended chains
$\mathfrak{s}\in \Sigma ^{nr}$
gives open-ended chains
 ${\mathbb{P}}^1(\gamma _{\mathfrak{s}},s_{\mathfrak{s}})$
from
${\mathbb{P}}^1(\gamma _{\mathfrak{s}},s_{\mathfrak{s}})$
from
 $\Gamma _{\mathfrak{s}}$
indexed by roots of
$\Gamma _{\mathfrak{s}}$
indexed by roots of
 $\overline{g_{\mathfrak{s}}}$
.
$\overline{g_{\mathfrak{s}}}$
. -
(6) Finally, blow down all
 $\Gamma _{\mathfrak{s}}$
where
$\Gamma _{\mathfrak{s}}$
where
 $\mathfrak{s}$
is a contractible cluster.
$\mathfrak{s}$
is a contractible cluster.
In (3) and (5), a chain indexed by
![]() $r$
goes from
$r$
goes from
![]() $\Gamma _{\mathfrak{s}}^r$
. In (3) the chain indexed by
$\Gamma _{\mathfrak{s}}^r$
. In (3) the chain indexed by
![]() $r_{\mathfrak{s},-}$
goes to
$r_{\mathfrak{s},-}$
goes to
![]() $\Gamma _{P(\mathfrak{s})}^{r_{P(\mathfrak{s}),-}}$
and the chain indexed by
$\Gamma _{P(\mathfrak{s})}^{r_{P(\mathfrak{s}),-}}$
and the chain indexed by
![]() $r_{\mathfrak{s},+}$
goes to
$r_{\mathfrak{s},+}$
goes to
![]() $\Gamma _{P(\mathfrak{s})}^{r_{P(\mathfrak{s}),+}}$
.
$\Gamma _{P(\mathfrak{s})}^{r_{P(\mathfrak{s}),+}}$
.
Before blowing down in (6), the components given in (1)–(5) describe the special fibre of a regular model of
![]() $C_{K^{nr}}$
with strict normal crossings.
$C_{K^{nr}}$
with strict normal crossings.
The Galois group
![]() $G_k$
acts naturally, that is for every
$G_k$
acts naturally, that is for every
![]() $\sigma \in G_k$
,
$\sigma \in G_k$
,
![]() $\sigma (\Gamma _{\mathfrak{s}}^r)=\Gamma _{\sigma (\mathfrak{s})}^{\sigma (r)}$
, and similarly, on the chains.
$\sigma (\Gamma _{\mathfrak{s}}^r)=\Gamma _{\sigma (\mathfrak{s})}^{\sigma (r)}$
, and similarly, on the chains.
If
![]() $\Gamma _{\mathfrak{s}}$
is irreducible, then its function field is isomorphic to
$\Gamma _{\mathfrak{s}}$
is irreducible, then its function field is isomorphic to
![]() $k^{\textrm{s}}(x)[y]$
with the relation
$k^{\textrm{s}}(x)[y]$
with the relation
![]() $y^{D_{\mathfrak{s}}}=\tilde{f_{\mathfrak{s}}}(x)$
.
$y^{D_{\mathfrak{s}}}=\tilde{f_{\mathfrak{s}}}(x)$
.
Remark 4.24.
Note that if
![]() $\Gamma _{\mathfrak{s}}$
or
$\Gamma _{\mathfrak{s}}$
or
![]() $\Gamma _{P(\mathfrak{s})}$
is reducible then
$\Gamma _{P(\mathfrak{s})}$
is reducible then
![]() $p_{\mathfrak{s}}/\gamma _{\mathfrak{s}}=2$
.
$p_{\mathfrak{s}}/\gamma _{\mathfrak{s}}=2$
.
Example 4.25.
Let
![]() $p$
be a prime number and let
$p$
be a prime number and let
![]() $a\in \mathbb{Z}_p$
,
$a\in \mathbb{Z}_p$
,
![]() $b\in \mathbb{Z}_p^\times$
such that the polynomial
$b\in \mathbb{Z}_p^\times$
such that the polynomial
![]() $x^2+ax+b$
is not a square modulo
$x^2+ax+b$
is not a square modulo
![]() $p$
. Let
$p$
. Let
![]() $C$
be the hyperelliptic curve over
$C$
be the hyperelliptic curve over
![]() $\mathbb{Q}_p$
of genus
$\mathbb{Q}_p$
of genus
![]() $4$
given by the equation
$4$
given by the equation
![]() $y^2=f(x)$
, where
$y^2=f(x)$
, where
![]() $f(x)=(x^6+ap^4x^3+bp^8)((x-p)^3-p^{11})$
. In Example 3.32
, we described the rational cluster picture of
$f(x)=(x^6+ap^4x^3+bp^8)((x-p)^3-p^{11})$
. In Example 3.32
, we described the rational cluster picture of
![]() $C$
and proved that
$C$
and proved that
![]() $C$
has an almost rational cluster picture. Recall that
$C$
has an almost rational cluster picture. Recall that
![]() $\Sigma _C^{\textrm{rat}}$
consists of
$\Sigma _C^{\textrm{rat}}$
consists of
![]() $3$
clusters
$3$
clusters
![]() $\mathfrak{t}_3,\mathfrak{t}_4,\mathfrak{R}$
of size
$\mathfrak{t}_3,\mathfrak{t}_4,\mathfrak{R}$
of size
![]() $6,3,9$
respectively such that
$6,3,9$
respectively such that
![]() $\mathfrak{t}_3\lt \mathfrak{R}$
and
$\mathfrak{t}_3\lt \mathfrak{R}$
and
![]() $\mathfrak{t}_4\lt \mathfrak{R}$
. In particular, note that
$\mathfrak{t}_4\lt \mathfrak{R}$
. In particular, note that
![]() $\Sigma _{\mathbb{Q}_p^{nr}}=\Sigma _C^{\textrm{rat}}$
, and no cluster of
$\Sigma _{\mathbb{Q}_p^{nr}}=\Sigma _C^{\textrm{rat}}$
, and no cluster of
![]() $\Sigma _{\mathbb{Q}_p^{nr}}$
is removable, so
$\Sigma _{\mathbb{Q}_p^{nr}}$
is removable, so
![]() $\Sigma ^{nr}=\Sigma _C^{\textrm{rat}}$
. The minimal elements of
$\Sigma ^{nr}=\Sigma _C^{\textrm{rat}}$
. The minimal elements of
![]() $\Sigma ^{nr}$
are then
$\Sigma ^{nr}$
are then
![]() $\mathfrak{t}_3$
and
$\mathfrak{t}_3$
and
![]() $\mathfrak{t}_4$
.
$\mathfrak{t}_4$
.
We want to describe the special fibre of the minimal regular model with normal crossings
![]() $\mathcal{C}^{\textrm{min}}$
of
$\mathcal{C}^{\textrm{min}}$
of
![]() $C$
. Compute the quantities in Definitions 4.6 and 4.13
, and the polynomials
$C$
. Compute the quantities in Definitions 4.6 and 4.13
, and the polynomials
![]() ${\overline{f_{\mathfrak{s}}}},{\overline{g_{\mathfrak{s}}}},{\overline{g_{\mathfrak{s}}^0}}$
of Definition 4.22
, for any cluster in
${\overline{f_{\mathfrak{s}}}},{\overline{g_{\mathfrak{s}}}},{\overline{g_{\mathfrak{s}}^0}}$
of Definition 4.22
, for any cluster in
![]() $\Sigma ^{nr}$
:
$\Sigma ^{nr}$
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where
![]() $\bar{a}, \bar{b}$
are the reductions of
$\bar{a}, \bar{b}$
are the reductions of
![]() $a,b$
modulo
$a,b$
modulo
![]() $p$
. Then
$p$
. Then
![]() $C$
is also
$C$
is also
![]() $y$
-regular for any
$y$
-regular for any
![]() $p$
. Following the steps of Theorem 4.23 the special fibre of
$p$
. Following the steps of Theorem 4.23 the special fibre of
![]() $\mathcal{C}^{\textrm{min}}$
over
$\mathcal{C}^{\textrm{min}}$
over
![]() $\bar{\mathbb{F}}_p$
can be described as follows:
$\bar{\mathbb{F}}_p$
can be described as follows:
-
(1) The clusters
 $\mathfrak{t}_3,\mathfrak{t}_4,\mathfrak{R}$
give
$\mathfrak{t}_3,\mathfrak{t}_4,\mathfrak{R}$
give
 $3$
irreducible components
$3$
irreducible components
 $\Gamma _{\mathfrak{t}_3},\Gamma _{\mathfrak{t}_4},\Gamma _{\mathfrak{R}}$
of genus
$\Gamma _{\mathfrak{t}_3},\Gamma _{\mathfrak{t}_4},\Gamma _{\mathfrak{R}}$
of genus
 $0$
of multiplicities
$0$
of multiplicities
 $6,6,2$
respectively;
$6,6,2$
respectively;
-
(2) The cluster
 $\mathfrak{t}_3$
gives
$\mathfrak{t}_3$
gives
 $2$
open-ended
$2$
open-ended
 ${\mathbb{P}}^1$
s of multiplicity
${\mathbb{P}}^1$
s of multiplicity
 $3$
from
$3$
from
 $\Gamma _{\mathfrak{t}_3}$
, while
$\Gamma _{\mathfrak{t}_3}$
, while
 $\mathfrak{t}_4$
gives
$\mathfrak{t}_4$
gives
 $1$
open-ended
$1$
open-ended
 ${\mathbb{P}}^1$
of multiplicity
${\mathbb{P}}^1$
of multiplicity
 $3$
from
$3$
from
 $\Gamma _{\mathfrak{t}_4}$
.
$\Gamma _{\mathfrak{t}_4}$
. -
(3) From
 $\gamma _{\mathfrak{t}_3}s_{\mathfrak{t}_3}=-\tfrac{1}{3}\gt -\tfrac{1}{2}\gt -1=\gamma _{\mathfrak{t}_3}\big (s_{\mathfrak{t}_3}-p_{\mathfrak{t}_3}\cdot \tfrac{\rho _{\mathfrak{t}_3}-\rho _{\mathfrak{R}}}{2}\big ),$
the cluster
$\gamma _{\mathfrak{t}_3}s_{\mathfrak{t}_3}=-\tfrac{1}{3}\gt -\tfrac{1}{2}\gt -1=\gamma _{\mathfrak{t}_3}\big (s_{\mathfrak{t}_3}-p_{\mathfrak{t}_3}\cdot \tfrac{\rho _{\mathfrak{t}_3}-\rho _{\mathfrak{R}}}{2}\big ),$
the cluster
 $\mathfrak{t}_3$
gives
$\mathfrak{t}_3$
gives
 $1$
$1$
 ${\mathbb{P}}^1$
of multiplicity
${\mathbb{P}}^1$
of multiplicity
 $4$
from
$4$
from
 $\Gamma _{\mathfrak{t}_3}$
to
$\Gamma _{\mathfrak{t}_3}$
to
 $\Gamma _{\mathfrak{R}}$
. From
the cluster
$\Gamma _{\mathfrak{R}}$
. From
the cluster \begin{align*} \gamma _{\mathfrak{t}_4}s_{\mathfrak{t}_4}=-\tfrac{7}{6}\gt -\tfrac{6}{5}\gt -\tfrac{5}{4}\gt -\tfrac{4}{3}\gt -\tfrac{3}{2}\gt -2\gt -\tfrac{5}{2}=\gamma _{\mathfrak{t}_3}\big (s_{\mathfrak{t}_4}-p_{\mathfrak{t}_4}\cdot \tfrac{\rho _{\mathfrak{t}_4}-\rho _{\mathfrak{R}}}{2}\big ) \end{align*}
\begin{align*} \gamma _{\mathfrak{t}_4}s_{\mathfrak{t}_4}=-\tfrac{7}{6}\gt -\tfrac{6}{5}\gt -\tfrac{5}{4}\gt -\tfrac{4}{3}\gt -\tfrac{3}{2}\gt -2\gt -\tfrac{5}{2}=\gamma _{\mathfrak{t}_3}\big (s_{\mathfrak{t}_4}-p_{\mathfrak{t}_4}\cdot \tfrac{\rho _{\mathfrak{t}_4}-\rho _{\mathfrak{R}}}{2}\big ) \end{align*}
 $\mathfrak{t}_4$
gives
$\mathfrak{t}_4$
gives
 $1$
chain of
$1$
chain of
 ${\mathbb{P}}^1$
s of multiplicities
${\mathbb{P}}^1$
s of multiplicities
 $5,4,3,2,1$
from
$5,4,3,2,1$
from
 $\Gamma _{\mathfrak{t}_4}$
to
$\Gamma _{\mathfrak{t}_4}$
to
 $\Gamma _{\mathfrak{R}}$
.
$\Gamma _{\mathfrak{R}}$
.
-
(4) From
 $-\gamma _{\mathfrak{t}_3}^0s_{\mathfrak{t}_3}^0=\tfrac{25}{3}\gt 8\gt 7$
the cluster
$-\gamma _{\mathfrak{t}_3}^0s_{\mathfrak{t}_3}^0=\tfrac{25}{3}\gt 8\gt 7$
the cluster
 $\mathfrak{t}_3$
gives
$\mathfrak{t}_3$
gives
 $1$
open-ended
$1$
open-ended
 ${\mathbb{P}}^1$
of multiplicity
${\mathbb{P}}^1$
of multiplicity
 $2$
from
$2$
from
 $\Gamma _{\mathfrak{t}_3}$
. From
$\Gamma _{\mathfrak{t}_3}$
. From
 $-\gamma _{\mathfrak{t}_4}^0s_{\mathfrak{t}_4}^0=\tfrac{29}{3}\gt \tfrac{19}{2}\gt 9\gt 8$
, the cluster
$-\gamma _{\mathfrak{t}_4}^0s_{\mathfrak{t}_4}^0=\tfrac{29}{3}\gt \tfrac{19}{2}\gt 9\gt 8$
, the cluster
 $\mathfrak{t}_4$
gives
$\mathfrak{t}_4$
gives
 $1$
open-ended chain of
$1$
open-ended chain of
 ${\mathbb{P}}^1$
s of multiplicities
${\mathbb{P}}^1$
s of multiplicities
 $4,2$
from
$4,2$
from
 $\Gamma _{\mathfrak{t}_4}$
.
$\Gamma _{\mathfrak{t}_4}$
. -
(5) From
 $\gamma _{\mathfrak{R}}s_{\mathfrak{R}}=\tfrac{1}{2}\gt 0\gt -1$
, the cluster
$\gamma _{\mathfrak{R}}s_{\mathfrak{R}}=\tfrac{1}{2}\gt 0\gt -1$
, the cluster
 $\mathfrak{R}$
gives
$\mathfrak{R}$
gives
 $1$
open-ended
$1$
open-ended
 ${\mathbb{P}}^1$
of multiplicity
${\mathbb{P}}^1$
of multiplicity
 $1$
from
$1$
from
 $\Gamma _{\mathfrak{R}}$
.
$\Gamma _{\mathfrak{R}}$
. -
(6) There is no contractible cluster, so the components we considered in the steps above describe the special fibre of
 $\mathcal{C}^{\textrm{min}}$
over
$\mathcal{C}^{\textrm{min}}$
over
 $\bar{\mathbb{F}}_p$
:
$\bar{\mathbb{F}}_p$
:
Finally, from the Galois action on the roots of the polynomials
![]() ${\overline{f_{\mathfrak{s}}}},{\overline{g_{\mathfrak{s}}}},{\overline{g_{\mathfrak{s}}^0}}$
, for
${\overline{f_{\mathfrak{s}}}},{\overline{g_{\mathfrak{s}}}},{\overline{g_{\mathfrak{s}}^0}}$
, for
![]() $\mathfrak{s}\in \Sigma ^{nr}$
, we get that
$\mathfrak{s}\in \Sigma ^{nr}$
, we get that
![]() $G_k$
acts trivially if
$G_k$
acts trivially if
![]() $x^2+\bar{a} x+\bar{b}$
is reducible in
$x^2+\bar{a} x+\bar{b}$
is reducible in
![]() ${\mathbb{F}}_p$
, while it swaps the two components of multiplicity
${\mathbb{F}}_p$
, while it swaps the two components of multiplicity
![]() $3$
intersecting
$3$
intersecting
![]() $\Gamma _{\mathfrak{t}_3}$
(coming from (2)) otherwise.
$\Gamma _{\mathfrak{t}_3}$
(coming from (2)) otherwise.
As application of Theorem 4.23 we suppose
![]() $k$
is finite of characteristic
$k$
is finite of characteristic
![]() $p\gt 2$
and
$p\gt 2$
and
![]() $C$
is semistable of genus
$C$
is semistable of genus
![]() $g\geq 2$
. In this setting [Reference Dokchitser, Dokchitser, Maistret and Morgan14, Theorem 8.5] describes the minimal regular model of
$g\geq 2$
. In this setting [Reference Dokchitser, Dokchitser, Maistret and Morgan14, Theorem 8.5] describes the minimal regular model of
![]() $C$
in terms of its cluster picture
$C$
in terms of its cluster picture
![]() $\Sigma _C$
. We compare that result with the one obtained from Theorem 4.23 (Corollary 4.27).
$\Sigma _C$
. We compare that result with the one obtained from Theorem 4.23 (Corollary 4.27).
First note that
![]() $C_{K^{nr}}$
is
$C_{K^{nr}}$
is
![]() $y$
-regular as
$y$
-regular as
![]() $p\neq 2$
. From [Reference Dokchitser, Dokchitser, Maistret and Morgan14, Definition 1.7], if
$p\neq 2$
. From [Reference Dokchitser, Dokchitser, Maistret and Morgan14, Definition 1.7], if
![]() $C$
is semistable then
$C$
is semistable then
-
(1) the extension
 $K(\mathfrak{R})/K$
has ramification degree at most
$K(\mathfrak{R})/K$
has ramification degree at most
 $2$
;
$2$
; -
(2) every proper cluster is
 $\textrm{Gal}(K^{\textrm{s}}/K^{nr})$
-invariant;
$\textrm{Gal}(K^{\textrm{s}}/K^{nr})$
-invariant; -
(3) every principal cluster has
 $d_{\mathfrak{s}}\in \mathbb{Z}$
and
$d_{\mathfrak{s}}\in \mathbb{Z}$
and
 $\nu _{\mathfrak{s}}\in 2\mathbb{Z}$
.
$\nu _{\mathfrak{s}}\in 2\mathbb{Z}$
.
It follows from Corollary 3.27 that
![]() $C_{K^{nr}}$
has an almost rational cluster picture.
$C_{K^{nr}}$
has an almost rational cluster picture.
In fact, (1) and (2) imply
![]() $\rho _{\mathfrak{s}}=d_{\mathfrak{s}}$
and
$\rho _{\mathfrak{s}}=d_{\mathfrak{s}}$
and
![]() $\epsilon _{\mathfrak{s}}=\nu _{\mathfrak{s}}$
for any proper cluster
$\epsilon _{\mathfrak{s}}=\nu _{\mathfrak{s}}$
for any proper cluster
![]() $\mathfrak{s}$
(Remark 3.13). In particular,
$\mathfrak{s}$
(Remark 3.13). In particular,
![]() $\Sigma _{C_{K^{nr}}}^{\textrm{rat}}=\Sigma _C$
. We will then say that
$\Sigma _{C_{K^{nr}}}^{\textrm{rat}}=\Sigma _C$
. We will then say that
![]() $\mathfrak{s}\in \Sigma _C$
is non-removable if
$\mathfrak{s}\in \Sigma _C$
is non-removable if
![]() $\mathfrak{s}$
is proper and non-removable as rational cluster in
$\mathfrak{s}$
is proper and non-removable as rational cluster in
![]() $\Sigma _{K^{nr}}$
.
$\Sigma _{K^{nr}}$
.
Lemma 4.26.
Suppose
![]() $k$
finite and
$k$
finite and
![]() $p\gt 2$
. Assume
$p\gt 2$
. Assume
![]() $C$
is semistable and let
$C$
is semistable and let
![]() $\mathfrak{s}\in \Sigma _C$
be a non-removable cluster. Then
$\mathfrak{s}\in \Sigma _C$
be a non-removable cluster. Then
![]() $d_{\mathfrak{s}}\in \frac{1}{2}\mathbb{Z}$
and
$d_{\mathfrak{s}}\in \frac{1}{2}\mathbb{Z}$
and
![]() $\nu _{\mathfrak{s}}\in \mathbb{Z}$
. Moreover,
$\nu _{\mathfrak{s}}\in \mathbb{Z}$
. Moreover,
![]() $\mathfrak{s}$
is contractible if and only if
$\mathfrak{s}$
is contractible if and only if
![]() $d_{\mathfrak{s}}\notin \mathbb{Z}$
or
$d_{\mathfrak{s}}\notin \mathbb{Z}$
or
![]() $\nu _{\mathfrak{s}}\notin 2\mathbb{Z}$
.
$\nu _{\mathfrak{s}}\notin 2\mathbb{Z}$
.
Proof. Let
![]() $\mathfrak{s}\in \Sigma _C$
be a non-removable cluster. Since
$\mathfrak{s}\in \Sigma _C$
be a non-removable cluster. Since
![]() $K(\mathfrak{R})/K$
has ramification degree at most
$K(\mathfrak{R})/K$
has ramification degree at most
![]() $2$
, then
$2$
, then
![]() $d_{\mathfrak{s}}\in \tfrac{1}{2}\mathbb{Z}$
.
$d_{\mathfrak{s}}\in \tfrac{1}{2}\mathbb{Z}$
.
By Theorem 4.23 the multiplicity of the
![]() $1$
-dimensional scheme
$1$
-dimensional scheme
![]() $\Gamma _{\mathfrak{s}}$
is
$\Gamma _{\mathfrak{s}}$
is
![]() $m_{\mathfrak{s}}$
. Furthermore,
$m_{\mathfrak{s}}$
. Furthermore,
![]() $\Gamma _{\mathfrak{s}}$
is an irreducible component of the special fibre of the minimal regular model of
$\Gamma _{\mathfrak{s}}$
is an irreducible component of the special fibre of the minimal regular model of
![]() $C$
if and only if
$C$
if and only if
![]() $\mathfrak{s}$
is not contractible. Therefore if
$\mathfrak{s}$
is not contractible. Therefore if
![]() $\mathfrak{s}$
is not contractible, then
$\mathfrak{s}$
is not contractible, then
![]() $m_{\mathfrak{s}}=1$
, that is
$m_{\mathfrak{s}}=1$
, that is
![]() $D_{\mathfrak{s}}=2$
and
$D_{\mathfrak{s}}=2$
and
![]() $b_{\mathfrak{s}}=1$
. It follows that
$b_{\mathfrak{s}}=1$
. It follows that
![]() $\nu _{\mathfrak{s}}\in 2\mathbb{Z}$
and
$\nu _{\mathfrak{s}}\in 2\mathbb{Z}$
and
![]() $d_{\mathfrak{s}}\in \mathbb{Z}$
. Suppose
$d_{\mathfrak{s}}\in \mathbb{Z}$
. Suppose
![]() $\mathfrak{s}$
contractible. Then either
$\mathfrak{s}$
contractible. Then either
![]() $d_{\mathfrak{s}}\notin \mathbb{Z}$
(and
$d_{\mathfrak{s}}\notin \mathbb{Z}$
(and
![]() $\nu _{\mathfrak{s}}\in \mathbb{Z}$
) or
$\nu _{\mathfrak{s}}\in \mathbb{Z}$
) or
![]() $\mathfrak{s}=\mathfrak{R}$
of size
$\mathfrak{s}=\mathfrak{R}$
of size
![]() $2g+2$
, with
$2g+2$
, with
![]() $2$
odd rational children and
$2$
odd rational children and
![]() $v(c_f)$
odd. We want to show that in the latter case,
$v(c_f)$
odd. We want to show that in the latter case,
![]() $\nu _{\mathfrak{s}}$
is odd. By Lemma 3.18,
$\nu _{\mathfrak{s}}$
is odd. By Lemma 3.18,
![]() $d_{\mathfrak{R}}\in \mathbb{Z}$
. Then
$d_{\mathfrak{R}}\in \mathbb{Z}$
. Then
![]() $\nu _{\mathfrak{R}}=v(c_f)+(2g+2)d_{\mathfrak{R}}$
is odd.
$\nu _{\mathfrak{R}}=v(c_f)+(2g+2)d_{\mathfrak{R}}$
is odd.
Let
![]() $\mathfrak{s}\in \Sigma _C$
be a non-removable cluster. By Lemma 4.26, if
$\mathfrak{s}\in \Sigma _C$
be a non-removable cluster. By Lemma 4.26, if
![]() $\mathfrak{s}$
is not contractible, then
$\mathfrak{s}$
is not contractible, then
![]() $2g(\mathfrak{s})+1$
or
$2g(\mathfrak{s})+1$
or
![]() $2g(\mathfrak{s})+2$
equals the number of odd children of
$2g(\mathfrak{s})+2$
equals the number of odd children of
![]() $\mathfrak{s}$
. In fact, this also holds when
$\mathfrak{s}$
. In fact, this also holds when
![]() $\mathfrak{s}$
is contractible since in that case
$\mathfrak{s}$
is contractible since in that case
![]() $g(\mathfrak{s})=0$
and
$g(\mathfrak{s})=0$
and
![]() $\mathfrak{s}$
has at most
$\mathfrak{s}$
has at most
![]() $2$
odd children.
$2$
odd children.
Corollary 4.27 (Minimal regular model (semistable reduction)). Suppose that
![]() $k$
is finite and
$k$
is finite and
![]() $p\gt 2$
. Let
$p\gt 2$
. Let
![]() $C/K$
be a semistable hyperelliptic curve of genus
$C/K$
be a semistable hyperelliptic curve of genus
![]() $g\geq 2$
. The minimal regular model
$g\geq 2$
. The minimal regular model
![]() $\mathcal{C}^{\textrm{min}}/O_{K^{nr}}$
of
$\mathcal{C}^{\textrm{min}}/O_{K^{nr}}$
of
![]() $C$
has special fibre
$C$
has special fibre
![]() $\mathcal{C}_s^{\textrm{min}}/k^{\textrm{s}}$
described as follows:
$\mathcal{C}_s^{\textrm{min}}/k^{\textrm{s}}$
described as follows:
-
(1) Every non-removable cluster
 $\mathfrak{s}\in \Sigma _C$
gives a
$\mathfrak{s}\in \Sigma _C$
gives a
 $1$
-dimensional subscheme
$1$
-dimensional subscheme
 $\Gamma _{\mathfrak{s}}$
. If
$\Gamma _{\mathfrak{s}}$
. If
 $\mathfrak{s}$
is übereven, then
$\mathfrak{s}$
is übereven, then
 $\Gamma _{\mathfrak{s}}$
is the disjoint union of
$\Gamma _{\mathfrak{s}}$
is the disjoint union of
 $\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}\simeq{\mathbb{P}}^1$
and
$\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}\simeq{\mathbb{P}}^1$
and
 $\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}\simeq{\mathbb{P}}^1$
, otherwise
$\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}\simeq{\mathbb{P}}^1$
, otherwise
 $\Gamma _{\mathfrak{s}}$
is irreducible of genus
$\Gamma _{\mathfrak{s}}$
is irreducible of genus
 $g(\mathfrak{s})$
(write
$g(\mathfrak{s})$
(write
 $\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}=\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}=\Gamma _{\mathfrak{s}}$
in this case). The indices
$\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}=\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}=\Gamma _{\mathfrak{s}}$
in this case). The indices
 $r_{\mathfrak{s},-}$
and
$r_{\mathfrak{s},-}$
and
 $r_{\mathfrak{s},+}$
are the roots of
$r_{\mathfrak{s},+}$
are the roots of
 $\overline{g_{\mathfrak{s}}}$
.
$\overline{g_{\mathfrak{s}}}$
. -
(2) Every odd proper cluster
 $\mathfrak{s}\in \Sigma _C$
, with size
$\mathfrak{s}\in \Sigma _C$
, with size
 $|\mathfrak{s}|\leq 2g$
, gives a chain of
$|\mathfrak{s}|\leq 2g$
, gives a chain of
 ${\mathbb{P}}^1$
s of length
${\mathbb{P}}^1$
s of length
 $\big \lfloor \frac{d_{\mathfrak{s}}-d_{P(\mathfrak{s})}-1}{2}\big \rfloor$
from
$\big \lfloor \frac{d_{\mathfrak{s}}-d_{P(\mathfrak{s})}-1}{2}\big \rfloor$
from
 $\Gamma _{\mathfrak{s}}$
to
$\Gamma _{\mathfrak{s}}$
to
 $\Gamma _{P(\mathfrak{s})}$
indexed by the root of
$\Gamma _{P(\mathfrak{s})}$
indexed by the root of
 $\overline{g_{\mathfrak{s}}}$
.
$\overline{g_{\mathfrak{s}}}$
. -
(3) Every even proper cluster
 $\mathfrak{s}\in \Sigma _C$
, with size
$\mathfrak{s}\in \Sigma _C$
, with size
 $|\mathfrak{s}|\leq 2g$
, gives a chain of
$|\mathfrak{s}|\leq 2g$
, gives a chain of
 ${\mathbb{P}}^1$
s of length
${\mathbb{P}}^1$
s of length
 $\left \lfloor d_{\mathfrak{s}}-d_{P(\mathfrak{s})}-\frac{1}{2}\right \rfloor$
from
$\left \lfloor d_{\mathfrak{s}}-d_{P(\mathfrak{s})}-\frac{1}{2}\right \rfloor$
from
 $\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}$
to
$\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},-}}$
to
 $\Gamma _{P(\mathfrak{s})}^{r_{P(\mathfrak{s}),-}}$
indexed by
$\Gamma _{P(\mathfrak{s})}^{r_{P(\mathfrak{s}),-}}$
indexed by
 $r_{\mathfrak{s},-}$
and a chain of
$r_{\mathfrak{s},-}$
and a chain of
 ${\mathbb{P}}^1$
s of same length from
${\mathbb{P}}^1$
s of same length from
 $\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}$
to
$\Gamma _{\mathfrak{s}}^{r_{\mathfrak{s},+}}$
to
 $\Gamma _{P(\mathfrak{s})}^{r_{P(\mathfrak{s}),+}}$
indexed by
$\Gamma _{P(\mathfrak{s})}^{r_{P(\mathfrak{s}),+}}$
indexed by
 $r_{\mathfrak{s},+}$
.
$r_{\mathfrak{s},+}$
. -
(4) Finally, blow down all
 $\Gamma _{\mathfrak{s}}$
where
$\Gamma _{\mathfrak{s}}$
where
 $\mathfrak{s}$
is a contractible cluster.
$\mathfrak{s}$
is a contractible cluster.
All components have multiplicity
![]() $1$
, and the absolute Galois group
$1$
, and the absolute Galois group
![]() $G_k$
acts naturally, as in Theorem 4.23.
$G_k$
acts naturally, as in Theorem 4.23.
Proof. Let
![]() $\mathfrak{s}\in \Sigma _C$
be a non-removable cluster. From Lemma 4.26, if
$\mathfrak{s}\in \Sigma _C$
be a non-removable cluster. From Lemma 4.26, if
![]() $\mathfrak{s}$
is not contractible, then
$\mathfrak{s}$
is not contractible, then
![]() $D_{\mathfrak{s}}=2$
,
$D_{\mathfrak{s}}=2$
,
![]() $\gamma _{\mathfrak{s}} s_{\mathfrak{s}}\in \mathbb{Z}$
and
$\gamma _{\mathfrak{s}} s_{\mathfrak{s}}\in \mathbb{Z}$
and
![]() $\gamma _{\mathfrak{s}}^0 s_{\mathfrak{s}}^0\in \mathbb{Z}$
. Suppose
$\gamma _{\mathfrak{s}}^0 s_{\mathfrak{s}}^0\in \mathbb{Z}$
. Suppose
![]() $\mathfrak{s}$
contractible. If
$\mathfrak{s}$
contractible. If
![]() $|\mathfrak{s}|=2$
with
$|\mathfrak{s}|=2$
with
![]() $d_{\mathfrak{s}}\notin \mathbb{Z}$
(case (1) of Definition 4.20), then
$d_{\mathfrak{s}}\notin \mathbb{Z}$
(case (1) of Definition 4.20), then
![]() $\gamma _{\mathfrak{s}}^0 s_{\mathfrak{s}}^0\in \mathbb{Z}$
and
$\gamma _{\mathfrak{s}}^0 s_{\mathfrak{s}}^0\in \mathbb{Z}$
and
![]() $\gamma _{\mathfrak{s}}=1$
,
$\gamma _{\mathfrak{s}}=1$
,
![]() $s_{\mathfrak{s}}\in \tfrac{1}{2}\mathbb{Z}\setminus \mathbb{Z}$
and so
$s_{\mathfrak{s}}\in \tfrac{1}{2}\mathbb{Z}\setminus \mathbb{Z}$
and so
![]() $s_{\mathfrak{s}}-d_{\mathfrak{s}}+d_{P(\mathfrak{s})}\in \mathbb{Z}$
, as
$s_{\mathfrak{s}}-d_{\mathfrak{s}}+d_{P(\mathfrak{s})}\in \mathbb{Z}$
, as
![]() $P(\mathfrak{s})$
can not be contractible. If
$P(\mathfrak{s})$
can not be contractible. If
![]() $\mathfrak{s}=\mathfrak{R}$
(cases (2), (3) of Definition 4.20), then
$\mathfrak{s}=\mathfrak{R}$
(cases (2), (3) of Definition 4.20), then
![]() $v(c_f)$
is odd, and so
$v(c_f)$
is odd, and so
![]() $\gamma _{\mathfrak{s}}=2$
and
$\gamma _{\mathfrak{s}}=2$
and
![]() $\gamma _{\mathfrak{s}} s_{\mathfrak{s}}\in \mathbb{Z}$
. Therefore (2), (4) and (5) of Theorem 4.23 do not give any components.
$\gamma _{\mathfrak{s}} s_{\mathfrak{s}}\in \mathbb{Z}$
. Therefore (2), (4) and (5) of Theorem 4.23 do not give any components.
Finally, as
![]() $\gamma _{\mathfrak{s}}=1$
and
$\gamma _{\mathfrak{s}}=1$
and
![]() $p_{\mathfrak{s}}\frac{d_{\mathfrak{s}}-d_{P(\mathfrak{s})}}{2}\in \frac{1}{2}\mathbb{Z}$
for any proper
$p_{\mathfrak{s}}\frac{d_{\mathfrak{s}}-d_{P(\mathfrak{s})}}{2}\in \frac{1}{2}\mathbb{Z}$
for any proper
![]() $\mathfrak{s}$
with size
$\mathfrak{s}$
with size
![]() $|\mathfrak{s}|\leq 2g$
(i.e. non-maximal), the length of
$|\mathfrak{s}|\leq 2g$
(i.e. non-maximal), the length of
![]() ${\mathbb{P}}^1(\gamma _{\mathfrak{s}},s_{\mathfrak{s}},s_{\mathfrak{s}}-p_{\mathfrak{s}}\cdot \frac{d_{\mathfrak{s}}-d_{P(\mathfrak{s})}}{2})$
is
${\mathbb{P}}^1(\gamma _{\mathfrak{s}},s_{\mathfrak{s}},s_{\mathfrak{s}}-p_{\mathfrak{s}}\cdot \frac{d_{\mathfrak{s}}-d_{P(\mathfrak{s})}}{2})$
is
The Corollary then follows from Theorem 4.23.
5. Construction of the model
We are going to construct a proper flat model
![]() $\mathcal{C}/O_K$
of
$\mathcal{C}/O_K$
of
![]() $C$
by glueing models defined in [Reference Dokchitser1, §4]. For this reason we will assume the reader has familiarity with the definitions and the results presented in that paper. Let us start this section by describing the strategy we will follow.
$C$
by glueing models defined in [Reference Dokchitser1, §4]. For this reason we will assume the reader has familiarity with the definitions and the results presented in that paper. Let us start this section by describing the strategy we will follow.
Let
![]() $\Sigma _C^{\textrm{min}}$
be the set of rationally minimal clusters of
$\Sigma _C^{\textrm{min}}$
be the set of rationally minimal clusters of
![]() $C$
and let
$C$
and let
![]() $\Sigma \subseteq \Sigma _C^{\textrm{min}}$
non-empty. For any cluster
$\Sigma \subseteq \Sigma _C^{\textrm{min}}$
non-empty. For any cluster
![]() $\mathfrak{s}\in \Sigma$
fix a rational centre
$\mathfrak{s}\in \Sigma$
fix a rational centre
![]() $w_{\mathfrak{s}}$
in such a way that
$w_{\mathfrak{s}}$
in such a way that
![]() $\mathring{\Sigma }_C^{w_{\mathfrak{s}}}$
consists of the proper clusters in
$\mathring{\Sigma }_C^{w_{\mathfrak{s}}}$
consists of the proper clusters in
![]() $\Sigma _C^{w_{\mathfrak{s}}}$
. This requirement can be satisfied by choosing
$\Sigma _C^{w_{\mathfrak{s}}}$
. This requirement can be satisfied by choosing
![]() $w_{\mathfrak{s}}\in \mathfrak{s}$
whenever possible.Footnote 3 Let
$w_{\mathfrak{s}}\in \mathfrak{s}$
whenever possible.Footnote 3 Let
![]() $W$
be the set of all such rational centres and define
$W$
be the set of all such rational centres and define
![]() $\Sigma ^W\;:\!=\;\bigcup _{w\in W}\Sigma _C^{w}$
. For every proper cluster
$\Sigma ^W\;:\!=\;\bigcup _{w\in W}\Sigma _C^{w}$
. For every proper cluster
![]() $\mathfrak{t}\in \Sigma ^W$
fix a rational centre
$\mathfrak{t}\in \Sigma ^W$
fix a rational centre
![]() $w_{\mathfrak{t}}\in W$
(Lemma 3.14). For every
$w_{\mathfrak{t}}\in W$
(Lemma 3.14). For every
![]() $w\in W$
, consider the curve
$w\in W$
, consider the curve
![]() $C^{w}\;:\;y^2=f(x+w)$
, isomorphic to
$C^{w}\;:\;y^2=f(x+w)$
, isomorphic to
![]() $C$
, and construct the (proper flat) model
$C$
, and construct the (proper flat) model
![]() $\mathcal{C}_\Delta ^{w}/O_K$
by [Reference Dokchitser1, §4, Theorem 3.14]. We will define an open subscheme
$\mathcal{C}_\Delta ^{w}/O_K$
by [Reference Dokchitser1, §4, Theorem 3.14]. We will define an open subscheme
![]() $\mathring{\mathcal{C}}_\Delta ^{w}$
of
$\mathring{\mathcal{C}}_\Delta ^{w}$
of
![]() $\mathcal{C}_\Delta ^{w}$
and we will show that glueing the schemes
$\mathcal{C}_\Delta ^{w}$
and we will show that glueing the schemes
![]() $\mathring{\mathcal{C}}_\Delta ^{w}$
, to varying of
$\mathring{\mathcal{C}}_\Delta ^{w}$
, to varying of
![]() $w\in W$
, along common opens, gives a proper flat model
$w\in W$
, along common opens, gives a proper flat model
![]() $\mathcal{C}/O_K$
of
$\mathcal{C}/O_K$
of
![]() $C$
. Furthermore, if
$C$
. Furthermore, if
![]() $\Sigma =\Sigma _C^{\textrm{min}}$
, and
$\Sigma =\Sigma _C^{\textrm{min}}$
, and
![]() $C$
is
$C$
is
![]() $y$
-regular and has an almost rational cluster picture, then
$y$
-regular and has an almost rational cluster picture, then
![]() $\mathring{\mathcal{C}}_\Delta ^{w}$
is an open regular subscheme of
$\mathring{\mathcal{C}}_\Delta ^{w}$
is an open regular subscheme of
![]() $\mathcal{C}_\Delta ^{w}$
and therefore
$\mathcal{C}_\Delta ^{w}$
and therefore
![]() $\mathcal{C}$
is also regular.
$\mathcal{C}$
is also regular.
5.1. Charts
Let
![]() $\Sigma =\{{\mathfrak{s}}_1\dots,{\mathfrak{s}}_m\}\subseteq \Sigma _C^{\textrm{min}}$
be a non-empty set of rationally minimal clusters and let
$\Sigma =\{{\mathfrak{s}}_1\dots,{\mathfrak{s}}_m\}\subseteq \Sigma _C^{\textrm{min}}$
be a non-empty set of rationally minimal clusters and let
![]() $W=\{w_1,\dots,w_m\}$
be a set of corresponding rational centres, such that
$W=\{w_1,\dots,w_m\}$
be a set of corresponding rational centres, such that
![]() $\mathring{\Sigma }_C^{w_h}$
consists of the proper clusters of
$\mathring{\Sigma }_C^{w_h}$
consists of the proper clusters of
![]() $\Sigma _C^{w_h}$
, for any
$\Sigma _C^{w_h}$
, for any
![]() $h=1,\dots,m$
. Define
$h=1,\dots,m$
. Define
![]() $\Sigma ^W\;:\!=\;\bigcup _{h=1}^m\Sigma _C^{w_h}$
. For any
$\Sigma ^W\;:\!=\;\bigcup _{h=1}^m\Sigma _C^{w_h}$
. For any
![]() $h,l=1,\dots,m$
,
$h,l=1,\dots,m$
,
![]() $h\neq l$
, define
$h\neq l$
, define
![]() $w_{hl}\;:\!=\;w_h-w_l$
, and write
$w_{hl}\;:\!=\;w_h-w_l$
, and write
![]() $w_{hl}=u_{hl}\pi ^{\rho _{hl}}$
, where
$w_{hl}=u_{hl}\pi ^{\rho _{hl}}$
, where
![]() $u_{hl}\in O_K^\times$
and
$u_{hl}\in O_K^\times$
and
![]() $\rho _{hl}\in \mathbb{Z}$
. Note that
$\rho _{hl}\in \mathbb{Z}$
. Note that
![]() $\rho _{hl}=\rho _{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}=\rho _{lh}$
, by Lemma 3.18. Set
$\rho _{hl}=\rho _{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}=\rho _{lh}$
, by Lemma 3.18. Set
![]() $u_{hh}\;:\!=\;0$
. Finally, for any
$u_{hh}\;:\!=\;0$
. Finally, for any
![]() $h,l=1,\dots,m$
, denote by
$h,l=1,\dots,m$
, denote by
![]() $\overline{u_{hl}}\in k$
the reduction of
$\overline{u_{hl}}\in k$
the reduction of
![]() $u_{hl}$
modulo
$u_{hl}$
modulo
![]() $\pi$
.
$\pi$
.
Definition 5.1.
Let
![]() $h=1,\dots,m$
and let
$h=1,\dots,m$
and let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Recall the matrices and cones defined in [
Reference Dokchitser1, §4]. We say that a matrix
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Recall the matrices and cones defined in [
Reference Dokchitser1, §4]. We say that a matrix
![]() $M$
is associated to
$M$
is associated to
![]() $\mathfrak{t}$
if either
$\mathfrak{t}$
if either
-
(i)
 $M=M_{L,i}$
, with
$M=M_{L,i}$
, with
 $L=L_{\mathfrak{t}}^{w_h}$
and
$L=L_{\mathfrak{t}}^{w_h}$
and
 $i=0,\dots,r_L$
or
$i=0,\dots,r_L$
or
-
(ii)
 $M=M_{V,j}$
, with
$M=M_{V,j}$
, with
 $V=V_{\mathfrak{t}}^{w_h}$
and
$V=V_{\mathfrak{t}}^{w_h}$
and
 $i=0,\dots,r_V$
or
$i=0,\dots,r_V$
or
-
(iii)
 $M=M_{V_0,j}$
, with
$M=M_{V_0,j}$
, with
 $V_0=V_0^{w_h}$
and
$V_0=V_0^{w_h}$
and
 $j=0,\dots,r_{V_0}$
, if
$j=0,\dots,r_{V_0}$
, if
 $\mathfrak{t}={\mathfrak{s}}_h$
.
$\mathfrak{t}={\mathfrak{s}}_h$
.
For a matrix
![]() $M$
associated to
$M$
associated to
![]() $\mathfrak{t}$
we denote by
$\mathfrak{t}$
we denote by
![]() $\delta _M$
and
$\delta _M$
and
![]() $\sigma _M$
respectively
$\sigma _M$
respectively
-
(i) the denominator
 $\delta _{L_{\mathfrak{t}}^{w_h}}$
and the cone
$\delta _{L_{\mathfrak{t}}^{w_h}}$
and the cone
 $\sigma _{L_{\mathfrak{t}}^{w_h},i,i+1}$
if
$\sigma _{L_{\mathfrak{t}}^{w_h},i,i+1}$
if
 $M=M_{L_{\mathfrak{t}}^{w_h},i}$
,
$M=M_{L_{\mathfrak{t}}^{w_h},i}$
, -
(ii) the denominator
 $\delta _{V_{\mathfrak{t}}^{w_h}}$
and the cone
$\delta _{V_{\mathfrak{t}}^{w_h}}$
and the cone
 $\sigma _{V_{\mathfrak{t}}^{w_h},j,j+1}$
if
$\sigma _{V_{\mathfrak{t}}^{w_h},j,j+1}$
if
 $M=M_{V_{\mathfrak{t}}^{w_h},j}$
,
$M=M_{V_{\mathfrak{t}}^{w_h},j}$
, -
(iii) the denominator
 $\delta _{V_0^{w_h}}$
and the cone
$\delta _{V_0^{w_h}}$
and the cone
 $\sigma _{V_0^{w_h},j,j+1}$
if
$\sigma _{V_0^{w_h},j,j+1}$
if
 $M=M_{V_0^{w_h},j}$
.
$M=M_{V_0^{w_h},j}$
.
Finally, define
![]() $X_M=\textrm{Spec}\, O_K[\sigma _M^\vee \cap \mathbb{Z}^3]$
and write
$X_M=\textrm{Spec}\, O_K[\sigma _M^\vee \cap \mathbb{Z}^3]$
and write
for the toric scheme defined in [
Reference Dokchitser1, §4.2] from the Newton polytope
![]() $\Delta _v^{w_h}$
associated to the curve
$\Delta _v^{w_h}$
associated to the curve
![]() $C^{w_h}$
. Therefore, by Lemma 4.3
, the union runs through every proper cluster
$C^{w_h}$
. Therefore, by Lemma 4.3
, the union runs through every proper cluster
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
and all matrices
$\mathfrak{t}\in \Sigma _C^{w_h}$
and all matrices
![]() $M$
associated to
$M$
associated to
![]() $\mathfrak{t}$
.
$\mathfrak{t}$
.
The following Lemma describes all possible matrices associated to
![]() $\mathfrak{t}$
.
$\mathfrak{t}$
.
Lemma 5.2.
Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Consider the
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Consider the
![]() $v$
-face
$v$
-face
![]() $F_{\mathfrak{t}}^{w_h}$
. Let
$F_{\mathfrak{t}}^{w_h}$
. Let
![]() $P_0,P_1\in \mathbb{Z}^2$
and
$P_0,P_1\in \mathbb{Z}^2$
and
![]() $n_i,d_i,k_i\in \mathbb{Z}$
be as in [
Reference Dokchitser1, §4] and define
$n_i,d_i,k_i\in \mathbb{Z}$
be as in [
Reference Dokchitser1, §4] and define
 \begin{align*} \delta \;:\!=\;\delta _M,\quad \gamma _i\;:\!=\;\frac{n_0d_i-n_id_0}{\delta d_0}\quad \mbox{ and }\quad T_i\;:\!=\;\left (\begin{matrix} \frac{1}{\delta } && -k_i&& k_{i+1}\\ 0 && \delta && 0\\ 0 && 0 && \delta \end{matrix}\right ), \end{align*}
\begin{align*} \delta \;:\!=\;\delta _M,\quad \gamma _i\;:\!=\;\frac{n_0d_i-n_id_0}{\delta d_0}\quad \mbox{ and }\quad T_i\;:\!=\;\left (\begin{matrix} \frac{1}{\delta } && -k_i&& k_{i+1}\\ 0 && \delta && 0\\ 0 && 0 && \delta \end{matrix}\right ), \end{align*}
for each matrix
![]() $M$
associated to
$M$
associated to
![]() $\mathfrak{t}$
.
$\mathfrak{t}$
.
-
Let
 $c$
be the unique element of
$c$
be the unique element of
 $\{0,\dots,b_{\mathfrak{t}}-1\}$
such that
$\{0,\dots,b_{\mathfrak{t}}-1\}$
such that
 $\tfrac{1}{b_{\mathfrak{t}}}-\rho _{\mathfrak{t}}\cdot c=d\in \mathbb{Z}$
. For
$\tfrac{1}{b_{\mathfrak{t}}}-\rho _{\mathfrak{t}}\cdot c=d\in \mathbb{Z}$
. For
 $L=L_{\mathfrak{t}}^{w_h}$
and for all
$L=L_{\mathfrak{t}}^{w_h}$
and for all
 $i=0,\dots,r_{L}$
, choose
$i=0,\dots,r_{L}$
, choose
 $k_i=cn_i+d\delta d_i(\lfloor \mathfrak{t}/2\rfloor +1)$
; then
$k_i=cn_i+d\delta d_i(\lfloor \mathfrak{t}/2\rfloor +1)$
; then
 $M_{L,i}$
and
$M_{L,i}$
and
 $M_{L,i}^{-1}$
are respectively
where
$M_{L,i}^{-1}$
are respectively
where \begin{align*} \left (\begin{matrix} \delta && -c\delta d_i\left (\tfrac{\epsilon _{\mathfrak{t}}}{2}+\gamma _i\right ) && c\delta d_{i+1}\left (\tfrac{\epsilon _{\mathfrak{t}}}{2}+\gamma _{i+1}\right )\\[4pt] 0 && d_i && -d_{i+1}\\[4pt] -\delta \rho _{\mathfrak{t}} && -d\delta d_i\left (\tfrac{\epsilon _{\mathfrak{t}}}{2}+\gamma _i\right ) && d\delta d_{i+1}\left (\tfrac{\epsilon _{\mathfrak{t}}}{2}+\gamma _{i+1}\right ) \end{matrix}\right ),\qquad T_i \cdot \left (\begin{matrix} 1 && \left \lfloor \frac{|\mathfrak{t}|}{2}\right \rfloor +1 && 0\\[4pt] d_{i+1}\rho _{\mathfrak{t}} && \frac{d_{i+1}\epsilon _{\mathfrak{t}}}{2}+\gamma _{i+1} && d_{i+1}\\[4pt] d_i\rho _{\mathfrak{t}} && \frac{d_i\epsilon _{\mathfrak{t}}}{2}+\gamma _i && d_i \end{matrix}\right ), \end{align*}
\begin{align*} \left (\begin{matrix} \delta && -c\delta d_i\left (\tfrac{\epsilon _{\mathfrak{t}}}{2}+\gamma _i\right ) && c\delta d_{i+1}\left (\tfrac{\epsilon _{\mathfrak{t}}}{2}+\gamma _{i+1}\right )\\[4pt] 0 && d_i && -d_{i+1}\\[4pt] -\delta \rho _{\mathfrak{t}} && -d\delta d_i\left (\tfrac{\epsilon _{\mathfrak{t}}}{2}+\gamma _i\right ) && d\delta d_{i+1}\left (\tfrac{\epsilon _{\mathfrak{t}}}{2}+\gamma _{i+1}\right ) \end{matrix}\right ),\qquad T_i \cdot \left (\begin{matrix} 1 && \left \lfloor \frac{|\mathfrak{t}|}{2}\right \rfloor +1 && 0\\[4pt] d_{i+1}\rho _{\mathfrak{t}} && \frac{d_{i+1}\epsilon _{\mathfrak{t}}}{2}+\gamma _{i+1} && d_{i+1}\\[4pt] d_i\rho _{\mathfrak{t}} && \frac{d_i\epsilon _{\mathfrak{t}}}{2}+\gamma _i && d_i \end{matrix}\right ), \end{align*}
 $P_0=(|\mathfrak{t}|,0)$
,
$P_0=(|\mathfrak{t}|,0)$
,
 $P_1=(\lfloor{|\mathfrak{t}|-1}/{2}\rfloor,1)$
and
$P_1=(\lfloor{|\mathfrak{t}|-1}/{2}\rfloor,1)$
and
 $\delta =\delta _{L}=b_{\mathfrak{t}}$
.
$\delta =\delta _{L}=b_{\mathfrak{t}}$
.
-
If
 $\mathfrak{t}$
is odd, then for
$\mathfrak{t}$
is odd, then for
 $V=V_{\mathfrak{t}}^{w_h}$
and for all
$V=V_{\mathfrak{t}}^{w_h}$
and for all
 $j=0,\dots, r_{V}$
, the matrices
$j=0,\dots, r_{V}$
, the matrices
 $M_{V,j}$
and
$M_{V,j}$
and
 $M_{V,j}^{-1}$
are respectively
where
$M_{V,j}^{-1}$
are respectively
where \begin{align*} \left (\begin{matrix} -|\mathfrak{t}| && -\frac{|\mathfrak{t}|+1}{2} d_j && \frac{|\mathfrak{t}|+1}{2}d_{j+1}\\[4pt] 2 && d_j &&-d_{j+1}\\[4pt] -\epsilon _{\mathfrak{t}}+|\mathfrak{t}|\rho _{\mathfrak{t}} && n_j &&-n_{j+1} \end{matrix}\right ),\qquad T_j\cdot \left (\begin{matrix} 1 && \frac{|\mathfrak{t}|+1}{2} && 0\\[4pt] d_{j+1}\rho _{\mathfrak{t}} -2\cdot \gamma _{j+1} && \frac{d_{j+1}\epsilon _{\mathfrak{t}}}{2}-|\mathfrak{t}|\cdot \gamma _{j+1}&& d_{j+1}\\[4pt] d_j\rho _{\mathfrak{t}} -2\cdot \gamma _{j} &&\frac{d_j\epsilon _{\mathfrak{t}}}{2}-|\mathfrak{t}|\cdot \gamma _j&& d_j \end{matrix}\right ), \end{align*}
\begin{align*} \left (\begin{matrix} -|\mathfrak{t}| && -\frac{|\mathfrak{t}|+1}{2} d_j && \frac{|\mathfrak{t}|+1}{2}d_{j+1}\\[4pt] 2 && d_j &&-d_{j+1}\\[4pt] -\epsilon _{\mathfrak{t}}+|\mathfrak{t}|\rho _{\mathfrak{t}} && n_j &&-n_{j+1} \end{matrix}\right ),\qquad T_j\cdot \left (\begin{matrix} 1 && \frac{|\mathfrak{t}|+1}{2} && 0\\[4pt] d_{j+1}\rho _{\mathfrak{t}} -2\cdot \gamma _{j+1} && \frac{d_{j+1}\epsilon _{\mathfrak{t}}}{2}-|\mathfrak{t}|\cdot \gamma _{j+1}&& d_{j+1}\\[4pt] d_j\rho _{\mathfrak{t}} -2\cdot \gamma _{j} &&\frac{d_j\epsilon _{\mathfrak{t}}}{2}-|\mathfrak{t}|\cdot \gamma _j&& d_j \end{matrix}\right ), \end{align*}
 $P_0=(|\mathfrak{t}|,0)$
,
$P_0=(|\mathfrak{t}|,0)$
,
 $P_1=(\lfloor{|\mathfrak{t}|-1}/{2}\rfloor,1)$
,
$P_1=(\lfloor{|\mathfrak{t}|-1}/{2}\rfloor,1)$
,
 $\delta =\delta _{V}=1$
and
$\delta =\delta _{V}=1$
and
 $k_j=k_{j+1}=0$
.
$k_j=k_{j+1}=0$
.
-
If
 $\mathfrak{t}$
is even, then for
$\mathfrak{t}$
is even, then for
 $V=V_{\mathfrak{t}}^{w_h}$
and for all
$V=V_{\mathfrak{t}}^{w_h}$
and for all
 $j=0,\dots, r_{V}$
, the matrices
$j=0,\dots, r_{V}$
, the matrices
 $M_{V,j}$
and
$M_{V,j}$
and
 $M_{V,j}^{-1}$
are respectively
$M_{V,j}^{-1}$
are respectively
 \begin{align*} \left (\begin{matrix} -\delta \frac{|\mathfrak{t}|}{2} && -\left (\frac{|\mathfrak{t}|}{2}+1\right ) d_j - k_j\frac{|\mathfrak{t}|}{2} && \left (\frac{|\mathfrak{t}|}{2}+1\right ) d_{j+1}+k_{j+1}\frac{|\mathfrak{t}|}{2}\\[4pt] \delta && d_j+k_j &&-d_{j+1}-k_{j+1}\\[4pt] -\delta \frac{\epsilon _{\mathfrak{t}}-|\mathfrak{t}|\rho _{\mathfrak{t}}}{2} && \frac{n_j}{\delta }-k_j\frac{\epsilon _{\mathfrak{t}}-|\mathfrak{t}|\rho _{\mathfrak{t}}}{2} &&-\frac{n_{j+1}}{\delta }+k_{j+1}\frac{\epsilon _{\mathfrak{t}}-|\mathfrak{t}|\rho _{\mathfrak{t}}}{2} \end{matrix}\right ), \end{align*}
where
\begin{align*} \left (\begin{matrix} -\delta \frac{|\mathfrak{t}|}{2} && -\left (\frac{|\mathfrak{t}|}{2}+1\right ) d_j - k_j\frac{|\mathfrak{t}|}{2} && \left (\frac{|\mathfrak{t}|}{2}+1\right ) d_{j+1}+k_{j+1}\frac{|\mathfrak{t}|}{2}\\[4pt] \delta && d_j+k_j &&-d_{j+1}-k_{j+1}\\[4pt] -\delta \frac{\epsilon _{\mathfrak{t}}-|\mathfrak{t}|\rho _{\mathfrak{t}}}{2} && \frac{n_j}{\delta }-k_j\frac{\epsilon _{\mathfrak{t}}-|\mathfrak{t}|\rho _{\mathfrak{t}}}{2} &&-\frac{n_{j+1}}{\delta }+k_{j+1}\frac{\epsilon _{\mathfrak{t}}-|\mathfrak{t}|\rho _{\mathfrak{t}}}{2} \end{matrix}\right ), \end{align*}
where \begin{align*} T_j\cdot \left (\begin{matrix} 1 && \frac{|\mathfrak{t}|}{2}+1 && 0\\[4pt] d_{j+1}\rho _{\mathfrak{t}} -\gamma _{j+1} && \frac{d_{j+1}\epsilon _{\mathfrak{t}}}{2}-\frac{|\mathfrak{t}|}{2}\gamma _{j+1}&& d_{j+1}\\[4pt] d_j\rho _{\mathfrak{t}} -\gamma _{j} && \frac{d_j\epsilon _{\mathfrak{t}}}{2} -\frac{|\mathfrak{t}|}{2}\gamma _{j}&& d_j \end{matrix}\right ), \end{align*}
\begin{align*} T_j\cdot \left (\begin{matrix} 1 && \frac{|\mathfrak{t}|}{2}+1 && 0\\[4pt] d_{j+1}\rho _{\mathfrak{t}} -\gamma _{j+1} && \frac{d_{j+1}\epsilon _{\mathfrak{t}}}{2}-\frac{|\mathfrak{t}|}{2}\gamma _{j+1}&& d_{j+1}\\[4pt] d_j\rho _{\mathfrak{t}} -\gamma _{j} && \frac{d_j\epsilon _{\mathfrak{t}}}{2} -\frac{|\mathfrak{t}|}{2}\gamma _{j}&& d_j \end{matrix}\right ), \end{align*}
 $P_0=(|\mathfrak{t}|,0)$
,
$P_0=(|\mathfrak{t}|,0)$
,
 $P_1=(\lfloor{|\mathfrak{t}|-1}/{2}\rfloor,1)$
and
$P_1=(\lfloor{|\mathfrak{t}|-1}/{2}\rfloor,1)$
and
 $\delta =\delta _{V}$
.
$\delta =\delta _{V}$
.
-
If
 $f(w_h)=0$
, then for
$f(w_h)=0$
, then for
 $V_0=V_0^{w_h}$
and for all
$V_0=V_0^{w_h}$
and for all
 $j=0,\dots, r_{V_0}$
, the matrices
$j=0,\dots, r_{V_0}$
, the matrices
 $M_{V_0,j}$
and
$M_{V_0,j}$
and
 $M_{V_0,j}^{-1}$
are respectively
where
$M_{V_0,j}^{-1}$
are respectively
where \begin{align*} \left (\begin{matrix} 1 && d_j && -d_{j+1}\\[4pt] -2 && -d_j &&d_{j+1}\\[4pt] \epsilon _{{\mathfrak{s}}_h}-\rho _{{\mathfrak{s}}_h} && n_j &&-n_{j+1} \end{matrix}\right ),\qquad T_j\cdot \left (\begin{matrix} -1 && -1 && 0\\[4pt] d_{j+1}\rho _{{\mathfrak{s}}_h} +2\cdot \gamma _{j+1} && \frac{d_{j+1}\epsilon _{{\mathfrak{s}}_h}}{2}+\gamma _{j+1}&& d_{j+1}\\[4pt] d_j\rho _{{\mathfrak{s}}_h} +2\cdot \gamma _{j} && \frac{d_j\epsilon _{{\mathfrak{s}}_h}}{2}+\gamma _{j}&& d_j \end{matrix}\right ), \end{align*}
\begin{align*} \left (\begin{matrix} 1 && d_j && -d_{j+1}\\[4pt] -2 && -d_j &&d_{j+1}\\[4pt] \epsilon _{{\mathfrak{s}}_h}-\rho _{{\mathfrak{s}}_h} && n_j &&-n_{j+1} \end{matrix}\right ),\qquad T_j\cdot \left (\begin{matrix} -1 && -1 && 0\\[4pt] d_{j+1}\rho _{{\mathfrak{s}}_h} +2\cdot \gamma _{j+1} && \frac{d_{j+1}\epsilon _{{\mathfrak{s}}_h}}{2}+\gamma _{j+1}&& d_{j+1}\\[4pt] d_j\rho _{{\mathfrak{s}}_h} +2\cdot \gamma _{j} && \frac{d_j\epsilon _{{\mathfrak{s}}_h}}{2}+\gamma _{j}&& d_j \end{matrix}\right ), \end{align*}
 $P_0=(0,2)$
,
$P_0=(0,2)$
,
 $P_1=(1,1)$
,
$P_1=(1,1)$
,
 $\delta =\delta _{V_0}=1$
and
$\delta =\delta _{V_0}=1$
and
 $k_j=k_{j+1}=0$
.
$k_j=k_{j+1}=0$
.
-
If
 $f(w_h)\neq 0$
, then for
$f(w_h)\neq 0$
, then for
 $V_0=V_0^{w_h}$
and for all
$V_0=V_0^{w_h}$
and for all
 $j=0,\dots, r_{V_0}$
, the matrices
$j=0,\dots, r_{V_0}$
, the matrices
 $M_{V_0,j}$
and
$M_{V_0,j}$
and
 $M_{V_0,j}^{-1}$
are respectively
where
$M_{V_0,j}^{-1}$
are respectively
where \begin{align*} \left (\begin{matrix} 0 && d_j && - d_{j+1}\\[4pt] -\delta && -d_j-k_j &&d_{j+1}+k_{j+1}\\[4pt] \delta \frac{\epsilon _{{\mathfrak{s}}_h}}{2} && \frac{n_j}{\delta }+k_j\frac{\epsilon _{{\mathfrak{s}}_h}}{2} &&-\frac{n_{j+1}}{\delta }-k_{j+1}\frac{\epsilon _{{\mathfrak{s}}_h}}{2} \end{matrix}\right ),\qquad T_j\cdot \left (\begin{matrix} -1 && -1 && 0\\[4pt] d_{j+1}\rho _{{\mathfrak{s}}_h} +\gamma _{j+1} && \frac{d_{j+1}\epsilon _{{\mathfrak{s}}_h}}{2}&& d_{j+1}\\[4pt] d_j\rho _{{\mathfrak{s}}_h} +\gamma _{j} && \frac{d_j\epsilon _{{\mathfrak{s}}_h}}{2}&& d_j \end{matrix}\right ), \end{align*}
\begin{align*} \left (\begin{matrix} 0 && d_j && - d_{j+1}\\[4pt] -\delta && -d_j-k_j &&d_{j+1}+k_{j+1}\\[4pt] \delta \frac{\epsilon _{{\mathfrak{s}}_h}}{2} && \frac{n_j}{\delta }+k_j\frac{\epsilon _{{\mathfrak{s}}_h}}{2} &&-\frac{n_{j+1}}{\delta }-k_{j+1}\frac{\epsilon _{{\mathfrak{s}}_h}}{2} \end{matrix}\right ),\qquad T_j\cdot \left (\begin{matrix} -1 && -1 && 0\\[4pt] d_{j+1}\rho _{{\mathfrak{s}}_h} +\gamma _{j+1} && \frac{d_{j+1}\epsilon _{{\mathfrak{s}}_h}}{2}&& d_{j+1}\\[4pt] d_j\rho _{{\mathfrak{s}}_h} +\gamma _{j} && \frac{d_j\epsilon _{{\mathfrak{s}}_h}}{2}&& d_j \end{matrix}\right ), \end{align*}
 $P_0=(0,2)$
,
$P_0=(0,2)$
,
 $P_1=(1,1)$
and
$P_1=(1,1)$
and
 $\delta =\delta _{V_0}$
.
$\delta =\delta _{V_0}$
.
Proof. We follow the notation of [Reference Dokchitser1, §4]. Choose
![]() $P_0,P_1\in \mathbb{Z}^2$
as in the proof of Lemma 4.3.
$P_0,P_1\in \mathbb{Z}^2$
as in the proof of Lemma 4.3.
First consider the edge
![]() $L_{\mathfrak{t}}^{w_h}$
of
$L_{\mathfrak{t}}^{w_h}$
of
![]() $F_{\mathfrak{t}}^{w_h}$
. From Lemma 4.3 we have
$F_{\mathfrak{t}}^{w_h}$
. From Lemma 4.3 we have
Then
![]() $M_{L_{\mathfrak{t}}^{w_h},i}$
and
$M_{L_{\mathfrak{t}}^{w_h},i}$
and
![]() $M_{L_{\mathfrak{t}}^{w_h},i}^{-1}$
follow from [Reference Dokchitser1, §4.3] as
$M_{L_{\mathfrak{t}}^{w_h},i}^{-1}$
follow from [Reference Dokchitser1, §4.3] as
![]() $k_i\equiv n_i(\delta \rho _{\mathfrak{t}})^{-1}\mod \delta$
and
$k_i\equiv n_i(\delta \rho _{\mathfrak{t}})^{-1}\mod \delta$
and
Now assume
![]() $\mathfrak{t}$
even and consider the edge
$\mathfrak{t}$
even and consider the edge
![]() $V_{\mathfrak{t}}^{w_h}$
of
$V_{\mathfrak{t}}^{w_h}$
of
![]() $F_{\mathfrak{t}}^{w_h}$
. Since
$F_{\mathfrak{t}}^{w_h}$
. Since
![]() $\mathfrak{t}$
is even,
$\mathfrak{t}$
is even,
and
![]() $(w_x,w_y)=\left (-\frac{|\mathfrak{t}|}{2}-1,1\right )$
as above. Then
$(w_x,w_y)=\left (-\frac{|\mathfrak{t}|}{2}-1,1\right )$
as above. Then
![]() $M_{V_{\mathfrak{t}}^{w_h},j}$
and
$M_{V_{\mathfrak{t}}^{w_h},j}$
and
![]() $M_{V_{\mathfrak{t}}^{w_h},j}^{-1}$
follow again from [Reference Dokchitser1, (4.3)] as
$M_{V_{\mathfrak{t}}^{w_h},j}^{-1}$
follow again from [Reference Dokchitser1, (4.3)] as
Similar arguments and computations yield the remaining matrices.
Remark 5.3.
From the Lemma above one can explicitly construct the charts of the model
![]() $\mathcal{C}_\Delta ^{w_h}$
. The description of its special fibre
$\mathcal{C}_\Delta ^{w_h}$
. The description of its special fibre
![]() $\mathcal{C}_{\Delta,s}^{w_h}$
which follows from [
Reference Dokchitser1, Theorem 3.14], matches the one given in Theorem 4.18 in the case
$\mathcal{C}_{\Delta,s}^{w_h}$
which follows from [
Reference Dokchitser1, Theorem 3.14], matches the one given in Theorem 4.18 in the case
![]() $W=\{w_h\}$
.
$W=\{w_h\}$
.
5.2. Open subschemes
Let
![]() $h=1,\dots,m$
and let
$h=1,\dots,m$
and let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Let
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Let
![]() $M$
be a matrix associated to
$M$
be a matrix associated to
![]() $\mathfrak{t}$
. Write
$\mathfrak{t}$
. Write
 \begin{align*} M=\begin{pmatrix} m_{11} && m_{12} && m_{13}\\[4pt] m_{21} && m_{22} && m_{23}\\[4pt] m_{31} && m_{32} && m_{33} \end{pmatrix}\qquad \mbox{and}\qquad M^{-1}=\begin{pmatrix} \tilde{m}_{11} &&\tilde{m}_{12} && \tilde{m}_{13}\\[4pt] \tilde{m}_{21} && \tilde{m}_{22} && \tilde{m}_{23}\\[4pt] \tilde{m}_{31} && \tilde{m}_{32} & &\tilde{m}_{33} \end{pmatrix} \end{align*}
\begin{align*} M=\begin{pmatrix} m_{11} && m_{12} && m_{13}\\[4pt] m_{21} && m_{22} && m_{23}\\[4pt] m_{31} && m_{32} && m_{33} \end{pmatrix}\qquad \mbox{and}\qquad M^{-1}=\begin{pmatrix} \tilde{m}_{11} &&\tilde{m}_{12} && \tilde{m}_{13}\\[4pt] \tilde{m}_{21} && \tilde{m}_{22} && \tilde{m}_{23}\\[4pt] \tilde{m}_{31} && \tilde{m}_{32} & &\tilde{m}_{33} \end{pmatrix} \end{align*}
Recall that
![]() $X_M=\textrm{Spec}\, R$
, where
$X_M=\textrm{Spec}\, R$
, where
via the change of variable
 \begin{align*} \left (\begin{matrix}X\\ Y\\ Z\\\end{matrix}\right )=\left (\begin{matrix}x^{m_{11}}y^{m_{21}}\pi ^{m_{31}}\\ x^{m_{12}}y^{m_{22}}\pi ^{m_{32}}\\ x^{m_{13}}y^{m_{23}}\pi ^{m_{33}}\end{matrix}\right )=\left (\begin{matrix}x\\ y\\ z\end{matrix}\right )\bullet M, \quad \left (\begin{matrix}x\\ y\\ \pi \end{matrix}\right )=\left (\begin{matrix}X^{\tilde{m}_{11}}Y^{\tilde{m}_{21}}Z^{\tilde{m}_{31}}\\ X^{\tilde{m}_{12}}Y^{\tilde{m}_{22}}Z^{\tilde{m}_{32}}\\ X^{\tilde{m}_{13}}Y^{\tilde{m}_{23}}Z^{\tilde{m}_{33}}\end{matrix}\right )=\left (\begin{matrix}X\\ Y\\ Z\end{matrix}\right )\bullet M^{-1}. \end{align*}
\begin{align*} \left (\begin{matrix}X\\ Y\\ Z\\\end{matrix}\right )=\left (\begin{matrix}x^{m_{11}}y^{m_{21}}\pi ^{m_{31}}\\ x^{m_{12}}y^{m_{22}}\pi ^{m_{32}}\\ x^{m_{13}}y^{m_{23}}\pi ^{m_{33}}\end{matrix}\right )=\left (\begin{matrix}x\\ y\\ z\end{matrix}\right )\bullet M, \quad \left (\begin{matrix}x\\ y\\ \pi \end{matrix}\right )=\left (\begin{matrix}X^{\tilde{m}_{11}}Y^{\tilde{m}_{21}}Z^{\tilde{m}_{31}}\\ X^{\tilde{m}_{12}}Y^{\tilde{m}_{22}}Z^{\tilde{m}_{32}}\\ X^{\tilde{m}_{13}}Y^{\tilde{m}_{23}}Z^{\tilde{m}_{33}}\end{matrix}\right )=\left (\begin{matrix}X\\ Y\\ Z\end{matrix}\right )\bullet M^{-1}. \end{align*}
Let
![]() $l\neq h$
. Set
$l\neq h$
. Set
 \begin{align*} T_M^{hl}(X,Y,Z)\;:\!=\;\begin{cases}1+u_{hl}X^{\rho _{hl}\tilde{m}_{13}-\tilde{m}_{11}}Y^{\rho _{hl}\tilde{m}_{23}-\tilde{m}_{21}}Z^{\rho _{hl}\tilde{m}_{33}-\tilde{m}_{31}}&\mbox{if }\mathfrak{t}\supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l,\\ u_{hl}^{-1}X^{\tilde{m}_{11}-\rho _{hl}\tilde{m}_{13}}Y^{\tilde{m}_{21}-\rho _{hl}\tilde{m}_{23}}Z^{\tilde{m}_{31}-\rho _{hl}\tilde{m}_{33}}+1&\mbox{if }\mathfrak{t}\not \supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l, \end{cases} \end{align*}
\begin{align*} T_M^{hl}(X,Y,Z)\;:\!=\;\begin{cases}1+u_{hl}X^{\rho _{hl}\tilde{m}_{13}-\tilde{m}_{11}}Y^{\rho _{hl}\tilde{m}_{23}-\tilde{m}_{21}}Z^{\rho _{hl}\tilde{m}_{33}-\tilde{m}_{31}}&\mbox{if }\mathfrak{t}\supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l,\\ u_{hl}^{-1}X^{\tilde{m}_{11}-\rho _{hl}\tilde{m}_{13}}Y^{\tilde{m}_{21}-\rho _{hl}\tilde{m}_{23}}Z^{\tilde{m}_{31}-\rho _{hl}\tilde{m}_{33}}+1&\mbox{if }\mathfrak{t}\not \supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l, \end{cases} \end{align*}
element of
![]() $R[Y^{-1},Z^{-1}]$
. Note that
$R[Y^{-1},Z^{-1}]$
. Note that
 \begin{align*} &\mbox{if}\quad \mathfrak{t}\supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l\quad \mbox{then}\quad T_M^{hl}(X,Y,Z)\stackrel{M}{\longmapsto }\frac{x+w_{hl}}{x},\\&\mbox{if}\quad \mathfrak{t}\not \supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l\quad \mbox{then}\quad T_M^{hl}(X,Y,Z)\stackrel{M}{\longmapsto }\frac{x+w_{hl}}{w_{hl}}. \end{align*}
\begin{align*} &\mbox{if}\quad \mathfrak{t}\supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l\quad \mbox{then}\quad T_M^{hl}(X,Y,Z)\stackrel{M}{\longmapsto }\frac{x+w_{hl}}{x},\\&\mbox{if}\quad \mathfrak{t}\not \supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l\quad \mbox{then}\quad T_M^{hl}(X,Y,Z)\stackrel{M}{\longmapsto }\frac{x+w_{hl}}{w_{hl}}. \end{align*}
The following two lemmas prove that
![]() $T_M^{hl}(X,Y,Z)\in R$
. Therefore, up to units,
$T_M^{hl}(X,Y,Z)\in R$
. Therefore, up to units,
![]() $T_M^{hl}(X,Y,Z)$
can be seen as the polynomial in
$T_M^{hl}(X,Y,Z)$
can be seen as the polynomial in
![]() $O_K[X^{\pm 1},Y,Z]$
satisfying
$O_K[X^{\pm 1},Y,Z]$
satisfying
with
![]() $n_X,n_Y,n_Z\in \mathbb{Z}$
, such that
$n_X,n_Y,n_Z\in \mathbb{Z}$
, such that
![]() $\textrm{ord}_Y(T_M^{hl})=\textrm{ord}_Z(T_M^{hl})=0$
.
$\textrm{ord}_Y(T_M^{hl})=\textrm{ord}_Z(T_M^{hl})=0$
.
Lemma 5.4.
Let
![]() $h,l=1,\dots,m$
, with
$h,l=1,\dots,m$
, with
![]() $h\neq l$
, let
$h\neq l$
, let
![]() $t\in \Sigma _C^{w_h}$
be such that
$t\in \Sigma _C^{w_h}$
be such that
![]() $\mathfrak{t}\supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and let
$\mathfrak{t}\supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and let
![]() $M$
be a matrix associated to
$M$
be a matrix associated to
![]() $\mathfrak{t}$
. Then
$\mathfrak{t}$
. Then
Furthermore if
![]() $M=M_{L_{\mathfrak{t}}^{w_h},i}$
then
$M=M_{L_{\mathfrak{t}}^{w_h},i}$
then
-
 $\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}=0$
if and only if
$\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}=0$
if and only if
 $i=r_{L_{\mathfrak{t}}^{w_h}}$
or
$i=r_{L_{\mathfrak{t}}^{w_h}}$
or
 $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
,
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, -
 $\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}=0$
if and only if
$\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}=0$
if and only if
 $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
;
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
;
if
![]() $M=M_{V_{\mathfrak{t}}^{w_h},j}$
then
$M=M_{V_{\mathfrak{t}}^{w_h},j}$
then
-
 $\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}\gt 0$
,
$\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}\gt 0$
, -
 $\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}=0$
if and only if
$\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}=0$
if and only if
 $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and
 $j=0$
.
$j=0$
.
Proof. This result follows from Lemma 5.2, which gives a complete description of
![]() $M$
and
$M$
and
![]() $M^{-1}$
. We show it when
$M^{-1}$
. We show it when
![]() $\mathfrak{t}$
is even and
$\mathfrak{t}$
is even and
![]() $M=M_{V_{\mathfrak{t}}^{w_h},j}$
, and leave the other cases for the reader. First of all recall that
$M=M_{V_{\mathfrak{t}}^{w_h},j}$
, and leave the other cases for the reader. First of all recall that
![]() $\rho _{hl}=\rho _{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}$
by Lemma 3.18. Then
$\rho _{hl}=\rho _{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}$
by Lemma 3.18. Then
where
![]() $\gamma _{j}=\tfrac{n_0d_j-n_jd_0}{\delta d_0}$
and
$\gamma _{j}=\tfrac{n_0d_j-n_jd_0}{\delta d_0}$
and
![]() $\delta =\delta _M$
. Similarly,
$\delta =\delta _M$
. Similarly,
In particular
![]() $\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}=0$
if and only if
$\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}=0$
if and only if
![]() $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and
![]() $j=0$
.
$j=0$
.
Lemma 5.5.
Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster such that
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster such that
![]() $\mathfrak{t}\not \supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, and let
$\mathfrak{t}\not \supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, and let
![]() $M$
be a matrix associated to
$M$
be a matrix associated to
![]() $\mathfrak{t}$
. Then
$\mathfrak{t}$
. Then
Furthermore,
![]() $\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}=0$
if and only if
$\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}=0$
if and only if
-
 $M=M_{L_{\mathfrak{t}}^{w_h},i}$
and
$M=M_{L_{\mathfrak{t}}^{w_h},i}$
and
 $i=r_{L_{\mathfrak{t}}^{w_h}}$
, or
$i=r_{L_{\mathfrak{t}}^{w_h}}$
, or
-
 $\mathfrak{t}\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
,
$\mathfrak{t}\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
,
 $M=M_{V_{\mathfrak{t}}^{w_h},j}$
, and
$M=M_{V_{\mathfrak{t}}^{w_h},j}$
, and
 $j=r_{V_{\mathfrak{t}}^{w_h}}$
.
$j=r_{V_{\mathfrak{t}}^{w_h}}$
.
Proof. This result follows again from Lemma 5.2. As in the previous lemma, we show it when
![]() $\mathfrak{t}$
is even and
$\mathfrak{t}$
is even and
![]() $M=M_{V_{\mathfrak{t}}^{w_h},j}$
, and leave the other cases for the reader.
$M=M_{V_{\mathfrak{t}}^{w_h},j}$
, and leave the other cases for the reader.
Let
![]() $r=r_{V_{\mathfrak{t}}^{w_h}}$
. Note that
$r=r_{V_{\mathfrak{t}}^{w_h}}$
. Note that
![]() $t\neq \mathfrak{R}$
. Set
$t\neq \mathfrak{R}$
. Set
![]() $\delta =\delta _M$
and
$\delta =\delta _M$
and
![]() $\gamma _j=\tfrac{n_0d_j-n_jd_0}{\delta d_0}$
. Then
$\gamma _j=\tfrac{n_0d_j-n_jd_0}{\delta d_0}$
. Then
since
![]() $d_j\gt 0$
and
$d_j\gt 0$
and
![]() $\gamma _j/d_j\lt \gamma _{r+1}/d_{r+1}=\rho _{\mathfrak{t}}-\rho _{P(\mathfrak{t})}.$
Similarly,
$\gamma _j/d_j\lt \gamma _{r+1}/d_{r+1}=\rho _{\mathfrak{t}}-\rho _{P(\mathfrak{t})}.$
Similarly,
In particular
![]() $\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}=0$
if and only if
$\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}=0$
if and only if
![]() $\mathfrak{t}\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and
$\mathfrak{t}\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and
![]() $j=r$
.
$j=r$
.
Let
and define
where
![]() $\mathfrak{t}$
runs through all proper clusters in
$\mathfrak{t}$
runs through all proper clusters in
![]() $\Sigma _C^{w_h}$
and
$\Sigma _C^{w_h}$
and
![]() $M$
runs through all matrices associated to
$M$
runs through all matrices associated to
![]() $\mathfrak{t}$
. We can then define the subscheme
$\mathfrak{t}$
. We can then define the subscheme
where
![]() $\mathcal{C}_{\Delta }^{w_h}/O_K$
is the model of the hyperelliptic curve
$\mathcal{C}_{\Delta }^{w_h}/O_K$
is the model of the hyperelliptic curve
![]() $C^{w_h}:y^2=f(x+w_h)$
described in [Reference Dokchitser1, Theorem 3.14] (see [Reference Dokchitser1, §4] for the construction). Explicitly, let
$C^{w_h}:y^2=f(x+w_h)$
described in [Reference Dokchitser1, Theorem 3.14] (see [Reference Dokchitser1, §4] for the construction). Explicitly, let
![]() $g_h(x,y)\;:\!=\;y^2-f(x+w_h)$
and define
$g_h(x,y)\;:\!=\;y^2-f(x+w_h)$
and define
![]() $\mathcal{F}_M^h\in O_K[X^{\pm 1},Y,Z]$
such that
$\mathcal{F}_M^h\in O_K[X^{\pm 1},Y,Z]$
such that
![]() $\textrm{ord}_Y(\mathcal{F}_M^h)=\textrm{ord}_Z(\mathcal{F}_M^h)=0$
, with all non-zero coefficients in
$\textrm{ord}_Y(\mathcal{F}_M^h)=\textrm{ord}_Z(\mathcal{F}_M^h)=0$
, with all non-zero coefficients in
![]() $O_K^\times$
, satisfying
$O_K^\times$
, satisfying
for unique
![]() $n_{Y,h},n_{Z,h}\in \mathbb{Z}$
. Consider the subscheme
$n_{Y,h},n_{Z,h}\in \mathbb{Z}$
. Consider the subscheme
Then
where
![]() $\mathfrak{t}$
runs through all proper clusters in
$\mathfrak{t}$
runs through all proper clusters in
![]() $\Sigma _C^{w_h}$
and
$\Sigma _C^{w_h}$
and
![]() $M$
runs through all matrices associated to
$M$
runs through all matrices associated to
![]() $\mathfrak{t}$
, as before.
$\mathfrak{t}$
, as before.
5.3. Glueing
Let
![]() $h,l=1,\dots,m$
, with
$h,l=1,\dots,m$
, with
![]() $h\neq l$
. Consider the isomorphism
$h\neq l$
. Consider the isomorphism
 \begin{equation} \phi :K\left [x^{\pm 1},y^{\pm 1},\prod _{o\neq l}(x+w_{lo})^{-1}\right ]\stackrel{\simeq }{\longrightarrow } K\left [x^{\pm 1},y^{\pm 1},\prod _{o\neq h}(x+w_{ho})^{-1}\right ] \end{equation}
\begin{equation} \phi :K\left [x^{\pm 1},y^{\pm 1},\prod _{o\neq l}(x+w_{lo})^{-1}\right ]\stackrel{\simeq }{\longrightarrow } K\left [x^{\pm 1},y^{\pm 1},\prod _{o\neq h}(x+w_{ho})^{-1}\right ] \end{equation}
sending
![]() $x\mapsto x+w_{hl}$
,
$x\mapsto x+w_{hl}$
,
![]() $y\mapsto y$
. If
$y\mapsto y$
. If
![]() $\mathfrak{t}\supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and
$\mathfrak{t}\supseteq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
and
![]() $M$
is a matrix associated to
$M$
is a matrix associated to
![]() $\mathfrak{t}$
, then
$\mathfrak{t}$
, then
![]() $\phi$
gives a map
$\phi$
gives a map
which sends
Hence it induces the isomorphisms
Via these maps we see that
![]() $g_h(x,y)=Y^{n_{Y,h}}Z^{n_{Z,h}}\mathcal{F}_M^h(X,Y,Z)$
also equals
$g_h(x,y)=Y^{n_{Y,h}}Z^{n_{Z,h}}\mathcal{F}_M^h(X,Y,Z)$
also equals
where
![]() $T_M^{hl}=T_M^{hl}(X,Y,Z)$
. Since neither
$T_M^{hl}=T_M^{hl}(X,Y,Z)$
. Since neither
![]() $Y$
nor
$Y$
nor
![]() $Z$
divide
$Z$
divide
![]() $T_M^{hl}(X,Y,Z)$
, we have
$T_M^{hl}(X,Y,Z)$
, we have
![]() $n_{Y,h}=n_{Y,l}$
,
$n_{Y,h}=n_{Y,l}$
,
![]() $n_{Z,h}=n_{Z,l}$
and
$n_{Z,h}=n_{Z,l}$
and
Hence (2) induces the isomorphisms
Define the subschemes
where
![]() $\mathfrak{t}_l$
runs through all proper clusters in
$\mathfrak{t}_l$
runs through all proper clusters in
![]() $\Sigma _C^{w_h}\cap \Sigma _C^{w_l}$
(i.e.
$\Sigma _C^{w_h}\cap \Sigma _C^{w_l}$
(i.e.
![]() $\mathfrak{t}_l\in \Sigma ^W$
,
$\mathfrak{t}_l\in \Sigma ^W$
,
![]() ${\mathfrak{s}}_h\wedge{\mathfrak{s}}_l\subseteq \mathfrak{t}_l$
) and
${\mathfrak{s}}_h\wedge{\mathfrak{s}}_l\subseteq \mathfrak{t}_l$
) and
![]() $M_l$
runs through all matrices associated to
$M_l$
runs through all matrices associated to
![]() $\mathfrak{t}_l$
. From (1), (2) and (3) we have isomorphisms of schemes
$\mathfrak{t}_l$
. From (1), (2) and (3) we have isomorphisms of schemes
Now,
![]() $U^{hl}\subset V^{hl}$
are open subschemes respectively of
$U^{hl}\subset V^{hl}$
are open subschemes respectively of
![]() $\mathring{\mathcal{C}}_\Delta ^{w_h}\subset{X}_\Delta ^h$
for any
$\mathring{\mathcal{C}}_\Delta ^{w_h}\subset{X}_\Delta ^h$
for any
![]() $l\neq h$
. Glueing the schemes
$l\neq h$
. Glueing the schemes
![]() $\mathring{\mathcal{C}}_\Delta ^{w_h}\subset{X}_\Delta ^h$
, to varying of
$\mathring{\mathcal{C}}_\Delta ^{w_h}\subset{X}_\Delta ^h$
, to varying of
![]() $h=1,\dots,m$
, respectively along the opens
$h=1,\dots,m$
, respectively along the opens
![]() $U^{hl}\subset V^{hl}$
via (4) gives the schemes
$U^{hl}\subset V^{hl}$
via (4) gives the schemes
![]() $\mathcal{C}\subset \mathcal{X}$
. We will show that
$\mathcal{C}\subset \mathcal{X}$
. We will show that
![]() $\mathcal{C}/O_K$
is a proper flatFootnote 4 model of
$\mathcal{C}/O_K$
is a proper flatFootnote 4 model of
![]() $C$
.
$C$
.
5.4. Generic fibre
We start studying the generic fibre
![]() $\mathcal{C}_\eta$
of
$\mathcal{C}_\eta$
of
![]() $\mathcal{C}$
. Since it is the glueing of all
$\mathcal{C}$
. Since it is the glueing of all
![]() $\mathring{\mathcal{C}}_{\Delta,\eta }^{w_h}$
through the glueing maps
$\mathring{\mathcal{C}}_{\Delta,\eta }^{w_h}$
through the glueing maps
induced by (4), we start focusing on
![]() $\mathring{\mathcal{C}}_{\Delta,\eta }^{w_h}$
for
$\mathring{\mathcal{C}}_{\Delta,\eta }^{w_h}$
for
![]() $h=1,\dots,m$
. In particular, as
$h=1,\dots,m$
. In particular, as
![]() $\mathring{\mathcal{C}}_\Delta ^{w_h}$
is an open subscheme of
$\mathring{\mathcal{C}}_\Delta ^{w_h}$
is an open subscheme of
![]() $\mathcal{C}_\Delta ^{w_h}$
, we study
$\mathcal{C}_\Delta ^{w_h}$
, we study
![]() $\mathcal{C}_{\Delta,\eta }^{w_h}\smallsetminus\mathring{\mathcal{C}}_{\Delta,\eta }^{w_h}=C^{w_h}\smallsetminus\mathring{\mathcal{C}}_{\Delta,\eta }^{w_h}$
.
$\mathcal{C}_{\Delta,\eta }^{w_h}\smallsetminus\mathring{\mathcal{C}}_{\Delta,\eta }^{w_h}=C^{w_h}\smallsetminus\mathring{\mathcal{C}}_{\Delta,\eta }^{w_h}$
.
Lemma 5.6.
For any
![]() $h=1,\dots,m$
,
$h=1,\dots,m$
,
Proof. For every choice of a proper cluster
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
, and
$\mathfrak{t}\in \Sigma _C^{w_h}$
, and
![]() $M$
associated to
$M$
associated to
![]() $\mathfrak{t}$
, let
$\mathfrak{t}$
, let
To study
![]() $P_M$
we are going to use Lemma 5.2 and the definition of
$P_M$
we are going to use Lemma 5.2 and the definition of
![]() $T_M^h(X,Y,Z)$
.
$T_M^h(X,Y,Z)$
.
Suppose first
![]() $\mathfrak{t}\neq \mathfrak{R}$
and
$\mathfrak{t}\neq \mathfrak{R}$
and
![]() $M=M_{V_{\mathfrak{t}}^{w_h},j}$
. Then
$M=M_{V_{\mathfrak{t}}^{w_h},j}$
. Then
![]() $\tilde{m}_{23},\tilde{m}_{33}\gt 0$
, so
$\tilde{m}_{23},\tilde{m}_{33}\gt 0$
, so
where the product runs over all
![]() $o\neq h$
. Now let
$o\neq h$
. Now let
![]() $\mathfrak{t}=\mathfrak{R}$
and
$\mathfrak{t}=\mathfrak{R}$
and
![]() $M=M_{V_{\mathfrak{t}}^{w_h},j}$
. If
$M=M_{V_{\mathfrak{t}}^{w_h},j}$
. If
![]() $j\neq r_{V_{\mathfrak{R}}^{w_h}}$
, then
$j\neq r_{V_{\mathfrak{R}}^{w_h}}$
, then
![]() $P_M$
is as in the previous case (since
$P_M$
is as in the previous case (since
![]() $\tilde{m}_{23},\tilde{m}_{33}\gt 0$
). If
$\tilde{m}_{23},\tilde{m}_{33}\gt 0$
). If
![]() $j= r_{V_{\mathfrak{R}}^{w_h}}$
, then
$j= r_{V_{\mathfrak{R}}^{w_h}}$
, then
![]() $\tilde{m}_{33}\gt 0$
,
$\tilde{m}_{33}\gt 0$
,
![]() $\tilde{m}_{23}=0$
, but
$\tilde{m}_{23}=0$
, but
![]() $\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}\gt 0$
by Lemma 5.4. So from the definition of
$\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}\gt 0$
by Lemma 5.4. So from the definition of
![]() $T_M^{hl}(X,Y,Z)$
we have once more the equality (5). Similarly, if
$T_M^{hl}(X,Y,Z)$
we have once more the equality (5). Similarly, if
![]() $\mathfrak{t}={\mathfrak{s}}_h$
and
$\mathfrak{t}={\mathfrak{s}}_h$
and
![]() $M=M_{V_0^{w_h},j}$
, then
$M=M_{V_0^{w_h},j}$
, then
![]() $\tilde{m}_{33}\gt 0$
, and
$\tilde{m}_{33}\gt 0$
, and
![]() $\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}\gt 0$
by Lemma 5.5. Hence we have (5) again.
$\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}\gt 0$
by Lemma 5.5. Hence we have (5) again.
It remains to study
![]() $P_M$
when
$P_M$
when
![]() $M=M_{L_{\mathfrak{t}}^{w_h},i}$
. If
$M=M_{L_{\mathfrak{t}}^{w_h},i}$
. If
![]() $i\neq r_{L_{\mathfrak{t}}^{w_h}}$
, then
$i\neq r_{L_{\mathfrak{t}}^{w_h}}$
, then
![]() $\tilde{m}_{23},\tilde{m}_{33}\gt 0$
and so
$\tilde{m}_{23},\tilde{m}_{33}\gt 0$
and so
![]() $P_M$
is as in (5). Let
$P_M$
is as in (5). Let
![]() $i=r_{L_{\mathfrak{t}}^{w_h}}$
. Then
$i=r_{L_{\mathfrak{t}}^{w_h}}$
. Then
![]() $\tilde{m}_{33}\gt 0$
but both
$\tilde{m}_{33}\gt 0$
but both
![]() $\tilde{m}_{23}$
and
$\tilde{m}_{23}$
and
![]() $\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}$
equal
$\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}$
equal
![]() $0$
. Hence
$0$
. Hence
![]() $\tilde{m}_{23}=\tilde{m}_{21}=0$
, which also implies
$\tilde{m}_{23}=\tilde{m}_{21}=0$
, which also implies
![]() $m_{21}=m_{23}=0$
. Therefore
$m_{21}=m_{23}=0$
. Therefore
![]() $M$
defines an isomorphism
$M$
defines an isomorphism
![]() $R[Z^{-1}]\simeq K[x^{\pm 1},y],$
which induces
$R[Z^{-1}]\simeq K[x^{\pm 1},y],$
which induces
This concludes the proof.
Regarding
![]() $\mathcal{C}_\Delta ^{w_h}$
as a model of
$\mathcal{C}_\Delta ^{w_h}$
as a model of
![]() $C$
via the natural isomorphism
$C$
via the natural isomorphism
![]() $C\xrightarrow{\sim }C^{w_h}$
, we get
$C\xrightarrow{\sim }C^{w_h}$
, we get
Thus the generic fibre of
![]() $\mathcal{C}$
is isomorphic to
$\mathcal{C}$
is isomorphic to
![]() $C$
.
$C$
.
5.5. Special fibre
We now study the structure of the special fibre
![]() $\mathcal{C}_s$
of
$\mathcal{C}_s$
of
![]() $\mathcal{C}$
. As for the generic fibre, we consider
$\mathcal{C}$
. As for the generic fibre, we consider
for any
![]() $h=1,\dots,m$
. For every choice of a proper cluster
$h=1,\dots,m$
. For every choice of a proper cluster
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
, and
$\mathfrak{t}\in \Sigma _C^{w_h}$
, and
![]() $M$
associated to
$M$
associated to
![]() $\mathfrak{t}$
, let
$\mathfrak{t}$
, let
Lemma 5.7.
Let
![]() $M=M_{L,i}$
for
$M=M_{L,i}$
for
![]() $L=L_{\mathfrak{t}}^{w_h}$
. Let
$L=L_{\mathfrak{t}}^{w_h}$
. Let
![]() $l\neq h$
. If
$l\neq h$
. If
![]() $\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
, then
$\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
, then
![]() $T_M^{hl}(X,Y,Z)=X^{-1}(X+u_{hl})$
, otherwise
$T_M^{hl}(X,Y,Z)=X^{-1}(X+u_{hl})$
, otherwise
-
(i)
 $T_M^{hl}(X,Y,0)=1$
for
$T_M^{hl}(X,Y,0)=1$
for
 $i=0,\dots,r_L$
;
$i=0,\dots,r_L$
; -
(ii)
 $T_M^{hl}(X,0,Z)=1$
for
$T_M^{hl}(X,0,Z)=1$
for
 $i=0,\dots,r_L-1$
.
$i=0,\dots,r_L-1$
.
Proof. Fix
![]() $l\neq h$
. If
$l\neq h$
. If
![]() $\mathfrak{t}\not \supseteq{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
, then by Lemma 5.5, we have
$\mathfrak{t}\not \supseteq{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
, then by Lemma 5.5, we have
![]() $\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}\geq 0$
and
$\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}\geq 0$
and
![]() $\tilde{m}_{31}-\rho _{hl} \tilde{m}_{33}\gt 0$
. Moreover, if
$\tilde{m}_{31}-\rho _{hl} \tilde{m}_{33}\gt 0$
. Moreover, if
![]() $\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}=0$
, then
$\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}=0$
, then
![]() $i=r_L$
. Therefore the equalities in (i) and (ii) follow directly from the definition of
$i=r_L$
. Therefore the equalities in (i) and (ii) follow directly from the definition of
![]() $T_M^{hl}$
.
$T_M^{hl}$
.
On the other hand, if
![]() $\mathfrak{t}\supsetneq{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
, then by Lemma 5.4, we have
$\mathfrak{t}\supsetneq{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
, then by Lemma 5.4, we have
![]() $\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}\geq 0$
and
$\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}\geq 0$
and
![]() $\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}\gt 0$
. Moreover, if
$\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}\gt 0$
. Moreover, if
![]() $\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}=0$
, then
$\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}=0$
, then
![]() $i=r_L$
. Therefore we have (i) and (ii) again.
$i=r_L$
. Therefore we have (i) and (ii) again.
Finally, assume
![]() $\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
. Since
$\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
. Since
![]() $\rho _{\mathfrak{t}}=\rho _{hl}\in \mathbb{Z}$
, then
$\rho _{\mathfrak{t}}=\rho _{hl}\in \mathbb{Z}$
, then
![]() $\rho _{hl} \tilde{m}_{13} - \tilde{m}_{11}=-1$
. Hence
$\rho _{hl} \tilde{m}_{13} - \tilde{m}_{11}=-1$
. Hence
by Lemma 5.4.
Lemma 5.8.
Suppose
![]() $M=M_{L_{\mathfrak{t}}^{w_h},i}$
. Then
$M=M_{L_{\mathfrak{t}}^{w_h},i}$
. Then
where the product runs over all
![]() $l\neq h$
such that
$l\neq h$
such that
![]() $\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
.
$\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
.
Proof. Lemma 5.2 shows that
![]() $\tilde{m}_{33}$
is always different from
$\tilde{m}_{33}$
is always different from
![]() $0$
, while
$0$
, while
![]() $\tilde{m}_{23}=0$
if and only if
$\tilde{m}_{23}=0$
if and only if
![]() $i=r_{L_{\mathfrak{t}}^{w_h}}$
. Thus the result follows from Lemma 5.7.
$i=r_{L_{\mathfrak{t}}^{w_h}}$
. Thus the result follows from Lemma 5.7.
Lemma 5.9.
Let
![]() $f_h(x)=f(x+w_h)$
and
$f_h(x)=f(x+w_h)$
and
![]() $l\neq h$
. Let
$l\neq h$
. Let
![]() $L_{hl}=L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}$
and let
$L_{hl}=L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}$
and let
![]() $\mathfrak{t}_l\in \Sigma _C^{w_l}$
,
$\mathfrak{t}_l\in \Sigma _C^{w_l}$
,
![]() $\mathfrak{t}_l\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Then
$\mathfrak{t}_l\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Then
![]() $\overline{u_{lh}}$
is a multiple root of
$\overline{u_{lh}}$
is a multiple root of
![]() $\overline{f_h|_{L_{hl}}}$
of order
$\overline{f_h|_{L_{hl}}}$
of order
![]() $|\mathfrak{t}_l|$
.
$|\mathfrak{t}_l|$
.
Conversely, if
![]() $\Sigma =\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}=\Sigma _C^{\textrm{min}}$
,
$\Sigma =\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}=\Sigma _C^{\textrm{min}}$
,
![]() $C$
has an almost rational cluster picture and
$C$
has an almost rational cluster picture and
![]() $\bar \alpha \in \bar{k}$
is a multiple root of
$\bar \alpha \in \bar{k}$
is a multiple root of
![]() $\overline{f_h|_L}$
for some edge
$\overline{f_h|_L}$
for some edge
![]() $L$
of
$L$
of
![]() $\texttt{NP}(f_h)$
, then
$\texttt{NP}(f_h)$
, then
![]() $\bar \alpha ={\overline{u_{lh}}}$
and
$\bar \alpha ={\overline{u_{lh}}}$
and
![]() $L=L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}$
for some
$L=L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}$
for some
![]() $l\neq h$
.
$l\neq h$
.
Proof. For any proper cluster
![]() $\mathfrak{s}\in \Sigma _f$
, let
$\mathfrak{s}\in \Sigma _f$
, let
![]() $\lambda _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w_h)$
. Let
$\lambda _{\mathfrak{s}}=\min _{r\in \mathfrak{s}}v(r-w_h)$
. Let
![]() $\mathfrak{s}\in \Sigma _C^{w_l}$
, with
$\mathfrak{s}\in \Sigma _C^{w_l}$
, with
![]() ${\mathfrak{s}}_l\subseteq \mathfrak{s}\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Then
${\mathfrak{s}}_l\subseteq \mathfrak{s}\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Then
![]() $w_h$
is not rational centre of
$w_h$
is not rational centre of
![]() $\mathfrak{s}$
, and for every root
$\mathfrak{s}$
, and for every root
![]() $r\in \mathfrak{s}$
, one has
$r\in \mathfrak{s}$
, one has
as
![]() $v(r-w_l)\geq \rho _{\mathfrak{s}}\gt \rho _{hl}$
. Therefore
$v(r-w_l)\geq \rho _{\mathfrak{s}}\gt \rho _{hl}$
. Therefore
![]() $\lambda _{\mathfrak{s}}=\rho _{hl}\in \mathbb{Z}$
. In particular,
$\lambda _{\mathfrak{s}}=\rho _{hl}\in \mathbb{Z}$
. In particular,
![]() $|\lambda _{\mathfrak{s}}|_p\leq 1$
. Furthermore,
$|\lambda _{\mathfrak{s}}|_p\leq 1$
. Furthermore,
and so Theorem 3.24(i) implies that
![]() ${\overline{u_{lh}}}=\tfrac{w_{lh}}{\pi ^{\rho _{hl}}}\mod \pi$
is a multiple root of
${\overline{u_{lh}}}=\tfrac{w_{lh}}{\pi ^{\rho _{hl}}}\mod \pi$
is a multiple root of
![]() $\overline{f_h|_{L_{hl}}}$
, where
$\overline{f_h|_{L_{hl}}}$
, where
![]() $L_{hl}=L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}$
.
$L_{hl}=L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}$
.
Let
![]() $\mathfrak{t}_l\in \Sigma _C^{w_l}$
,
$\mathfrak{t}_l\in \Sigma _C^{w_l}$
,
![]() $\mathfrak{t}_l\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Since
$\mathfrak{t}_l\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Since
![]() ${\mathfrak{s}}_l\subseteq \mathfrak{t}_l\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
we have
${\mathfrak{s}}_l\subseteq \mathfrak{t}_l\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
we have
as
![]() $v(r-w_l)\gt \rho _{hl}$
if and only if
$v(r-w_l)\gt \rho _{hl}$
if and only if
![]() ${\overline{u_{lh}}}=\frac{r-w_h}{\pi ^{\rho _{hl}}}\mod \pi$
. Thus the multiplicity of
${\overline{u_{lh}}}=\frac{r-w_h}{\pi ^{\rho _{hl}}}\mod \pi$
. Thus the multiplicity of
![]() $\overline{u_{lh}}$
is
$\overline{u_{lh}}$
is
![]() $|\mathfrak{t}_l|$
by Theorem 3.24(ii).
$|\mathfrak{t}_l|$
by Theorem 3.24(ii).
Now let
![]() $\bar{\alpha }$
be a multiple root of
$\bar{\alpha }$
be a multiple root of
![]() $\overline{f_h|_L}$
for some edge
$\overline{f_h|_L}$
for some edge
![]() $L$
of
$L$
of
![]() $\texttt{NP}(f_h)$
and let
$\texttt{NP}(f_h)$
and let
![]() $\mathfrak{s}\in \Sigma _{f}$
associated to
$\mathfrak{s}\in \Sigma _{f}$
associated to
![]() $\bar{\alpha }$
by Theorem 3.24(iii). We want to prove that if
$\bar{\alpha }$
by Theorem 3.24(iii). We want to prove that if
![]() $C$
has an almost rational cluster picture and
$C$
has an almost rational cluster picture and
![]() $\Sigma =\Sigma _C^{\textrm{min}}$
, then there exists
$\Sigma =\Sigma _C^{\textrm{min}}$
, then there exists
![]() $l\neq h$
so that
$l\neq h$
so that
![]() $\bar \alpha ={\overline{u_{lh}}}$
. Note first
$\bar \alpha ={\overline{u_{lh}}}$
. Note first
![]() $w_h$
is not a rational centre of
$w_h$
is not a rational centre of
![]() $\mathfrak{s}$
. Indeed, if
$\mathfrak{s}$
. Indeed, if
![]() $w_h$
is a rational centre of
$w_h$
is a rational centre of
![]() $\mathfrak{s}$
, then
$\mathfrak{s}$
, then
which contradicts the fact that
![]() $C$
has an almost rational cluster picture. As
$C$
has an almost rational cluster picture. As
![]() $\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}=\Sigma _C^{\textrm{min}}$
, we must have that
$\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}=\Sigma _C^{\textrm{min}}$
, we must have that
![]() $w_{l}$
is a rational centre of
$w_{l}$
is a rational centre of
![]() $\mathfrak{s}$
, for some
$\mathfrak{s}$
, for some
![]() $l\neq h$
. Then
$l\neq h$
. Then
![]() ${\mathfrak{s}}_l\subseteq \mathfrak{s}\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Since
${\mathfrak{s}}_l\subseteq \mathfrak{s}\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Since
![]() $\bar \alpha =\tfrac{r-w_h}{\pi ^{\lambda _{\mathfrak{s}}}}\mod \pi$
for any
$\bar \alpha =\tfrac{r-w_h}{\pi ^{\lambda _{\mathfrak{s}}}}\mod \pi$
for any
![]() $r\in \mathfrak{s}$
, from above we have
$r\in \mathfrak{s}$
, from above we have
![]() $\bar \alpha ={\overline{u_{lh}}}$
. Finally,
$\bar \alpha ={\overline{u_{lh}}}$
. Finally,
![]() $L$
is the edge of
$L$
is the edge of
![]() $\texttt{NP}(f_h)$
of slope
$\texttt{NP}(f_h)$
of slope
![]() $-\lambda _{\mathfrak{s}}=-\rho _{hl}$
. Thus
$-\lambda _{\mathfrak{s}}=-\rho _{hl}$
. Thus
![]() $L=L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}$
.
$L=L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}$
.
It remains to compute
![]() $S_M$
when
$S_M$
when
![]() $M=M_{V,j}$
, where
$M=M_{V,j}$
, where
![]() $V=V_{\mathfrak{t}}^{w_h}$
or
$V=V_{\mathfrak{t}}^{w_h}$
or
![]() $V=V_0^{w_h}$
.
$V=V_0^{w_h}$
.
Lemma 5.10.
Let
![]() $M=M_{V,j}$
for
$M=M_{V,j}$
for
![]() $V=V_{\mathfrak{t}}^{w_h}$
, or
$V=V_{\mathfrak{t}}^{w_h}$
, or
![]() $V=V_0^{w_h}$
if
$V=V_0^{w_h}$
if
![]() $\mathfrak{t}={\mathfrak{s}}_h$
. For any
$\mathfrak{t}={\mathfrak{s}}_h$
. For any
![]() $l\neq h$
we have
$l\neq h$
we have
-
(i)
 $T_M^{hl}(X,Y,0)=1$
except when
$T_M^{hl}(X,Y,0)=1$
except when
 $\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and
$\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and
 $j=0$
;
$j=0$
; -
(ii)
 $T_M^{hl}(X,0,Z)=1$
except when
$T_M^{hl}(X,0,Z)=1$
except when
 $\mathfrak{t}\lt{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and
$\mathfrak{t}\lt{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and
 $j=r_V$
.
$j=r_V$
.
Proof. The Lemma immediately follows from Lemmas 5.4 and 5.5.
Lemma 5.11.
Let
![]() $M=M_{V,j}$
with
$M=M_{V,j}$
with
![]() $V=V_{\mathfrak{t}}^{w_h}$
, or
$V=V_{\mathfrak{t}}^{w_h}$
, or
![]() $V=V_0^{w_h}$
if
$V=V_0^{w_h}$
if
![]() $\mathfrak{t}={\mathfrak{s}}_h$
. Then
$\mathfrak{t}={\mathfrak{s}}_h$
. Then
![]() $S_M=\varnothing$
.
$S_M=\varnothing$
.
Proof. For any
![]() $l\neq h$
, we want to prove that
$l\neq h$
, we want to prove that
Lemma 5.2 shows that
![]() $\tilde{m}_{33}$
is always different from
$\tilde{m}_{33}$
is always different from
![]() $0$
and that
$0$
and that
![]() $\tilde{m}_{23}=0$
if and only if
$\tilde{m}_{23}=0$
if and only if
![]() $j=r_V$
, and
$j=r_V$
, and
![]() $V=V_{\mathfrak{R}}^{w_h}$
or
$V=V_{\mathfrak{R}}^{w_h}$
or
![]() $V=V_0^{w_h}$
. Assume that if
$V=V_0^{w_h}$
. Assume that if
![]() $\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
then
$\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
then
![]() $j\neq 0$
and that if
$j\neq 0$
and that if
![]() $\mathfrak{t}\lt{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
then
$\mathfrak{t}\lt{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
then
![]() $j\neq r_{V}$
. Lemma 5.10 implies (6).
$j\neq r_{V}$
. Lemma 5.10 implies (6).
If
![]() $\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and
$\mathfrak{t}={\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and
![]() $j=0$
, then
$j=0$
, then
![]() $\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}= 0$
but
$\rho _{hl} \tilde{m}_{33}-\tilde{m}_{31}= 0$
but
![]() $\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}\gt 0$
. So
$\rho _{hl} \tilde{m}_{23}-\tilde{m}_{21}\gt 0$
. So
Similarly, if
![]() $\mathfrak{t}\lt{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and
$\mathfrak{t}\lt{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and
![]() $j=r_{V}$
, then
$j=r_{V}$
, then
![]() $\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}= 0$
, however
$\tilde{m}_{21}-\rho _{hl} \tilde{m}_{23}= 0$
, however
![]() $\tilde{m}_{31}-\rho _{hl} \tilde{m}_{33}\gt 0$
. Then
$\tilde{m}_{31}-\rho _{hl} \tilde{m}_{33}\gt 0$
. Then
In both cases,
![]() $S_M^{hl}\subseteq X_{F}$
as sets, where
$S_M^{hl}\subseteq X_{F}$
as sets, where
![]() $F=F_{{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h}^{w_h}$
([Reference Dokchitser1, Definition 3.7]). Let
$F=F_{{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h}^{w_h}$
([Reference Dokchitser1, Definition 3.7]). Let
![]() $L=L_{{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h}^{w_h}$
, and let
$L=L_{{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h}^{w_h}$
, and let
![]() $f_h(x)=f(x+w_h)$
and
$f_h(x)=f(x+w_h)$
and
![]() $g_h(x,y)=y^2-f_h(x)$
. By Lemmas 5.8 and 5.9, one has
$g_h(x,y)=y^2-f_h(x)$
. By Lemmas 5.8 and 5.9, one has
as
![]() $\mathcal{F}_{M_{L,0}}^h(X,Y,0)\mod \pi$
equals
$\mathcal{F}_{M_{L,0}}^h(X,Y,0)\mod \pi$
equals
![]() $Y^b-X^a{\overline{f_h|_L}}(X)$
, for some
$Y^b-X^a{\overline{f_h|_L}}(X)$
, for some
![]() $a\in \mathbb{Z}$
,
$a\in \mathbb{Z}$
,
![]() $b=1,2$
(see Lemma 5.17 for more details, whose proof is independent of this result). Thus if
$b=1,2$
(see Lemma 5.17 for more details, whose proof is independent of this result). Thus if
![]() $V=V_{\mathfrak{t}}^{w_h}$
and
$V=V_{\mathfrak{t}}^{w_h}$
and
![]() $M=M_{V,j}$
, then
$M=M_{V,j}$
, then
![]() $S_M=\varnothing$
.
$S_M=\varnothing$
.
5.6. Components
Now that we have compared the special fibre of
![]() $\mathcal{C}$
with those of the models
$\mathcal{C}$
with those of the models
![]() $\mathcal{C}_{\Delta }^{w_h}$
, let us describe closed subschemes that form it. We will first study closed subschemes forming
$\mathcal{C}_{\Delta }^{w_h}$
, let us describe closed subschemes that form it. We will first study closed subschemes forming
![]() $\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
and then how they glue in
$\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
and then how they glue in
![]() $\mathcal{C}_s$
.
$\mathcal{C}_s$
.
Let
![]() $f_h(x)=f(x+w_h)$
and
$f_h(x)=f(x+w_h)$
and
![]() $g_h(x,y)=y^2-f_h(x)$
. According to [Reference Dokchitser1, Theorem 3.14] the special fibre of
$g_h(x,y)=y^2-f_h(x)$
. According to [Reference Dokchitser1, Theorem 3.14] the special fibre of
![]() $\mathcal{C}_\Delta ^{w_h}$
is formed by:
$\mathcal{C}_\Delta ^{w_h}$
is formed by:
-
Chains of
 ${\mathbb{P}}_k^1$
s coming from
${\mathbb{P}}_k^1$
s coming from
 $v$
-edges of
$v$
-edges of
 $\Delta ^{w_h}$
.
$\Delta ^{w_h}$
. -
 $1$
-dimensional subschemes coming from
$1$
-dimensional subschemes coming from
 $v$
-faces of
$v$
-faces of
 $\Delta ^{w_h}$
.
$\Delta ^{w_h}$
.
More precisely, each
![]() $v$
-edge
$v$
-edge
![]() $E$
gives a scheme
$E$
gives a scheme
![]() $X_E\times{\mathbb{P}}_E$
, where
$X_E\times{\mathbb{P}}_E$
, where
![]() ${\mathbb{P}}_E$
is a chain of
${\mathbb{P}}_E$
is a chain of
![]() ${\mathbb{P}}_k^1$
s and
${\mathbb{P}}_k^1$
s and
![]() $X_E\subset{\mathbb{G}}_{m,k}$
is given by
$X_E\subset{\mathbb{G}}_{m,k}$
is given by
![]() ${\overline{g_h|_E}}=0$
. The multiplicities and the length of
${\overline{g_h|_E}}=0$
. The multiplicities and the length of
![]() ${\mathbb{P}}_E$
can be completely described by the slopes of
${\mathbb{P}}_E$
can be completely described by the slopes of
![]() $E$
. On the other hand, each
$E$
. On the other hand, each
![]() $v$
-face
$v$
-face
![]() $F$
gives a proper scheme
$F$
gives a proper scheme
![]() $\bar{X}_{F}$
containing an open subscheme
$\bar{X}_{F}$
containing an open subscheme
![]() $X_F\subseteq{\mathbb{G}}_{m,k}^2$
given by
$X_F\subseteq{\mathbb{G}}_{m,k}^2$
given by
![]() ${\overline{g_h|_F}}=0$
. How the previous schemes intersect to form
${\overline{g_h|_F}}=0$
. How the previous schemes intersect to form
![]() $\mathcal{C}_{\Delta,s}^{w_h}$
is described by [Reference Dokchitser1, Theorem 3.14]. The reader is pointed to [Reference Dokchitser1] for more details.
$\mathcal{C}_{\Delta,s}^{w_h}$
is described by [Reference Dokchitser1, Theorem 3.14]. The reader is pointed to [Reference Dokchitser1] for more details.
Definition 5.12.
Let
![]() $\mathfrak{t}\in \Sigma ^W$
be a proper cluster. For any rational centre
$\mathfrak{t}\in \Sigma ^W$
be a proper cluster. For any rational centre
![]() $w$
of
$w$
of
![]() $\mathfrak{t}$
, let
$\mathfrak{t}$
, let
![]() $r_{\mathfrak{t},w}=\tfrac{w-r}{\pi ^{\rho _{\mathfrak{t}}}}$
,
$r_{\mathfrak{t},w}=\tfrac{w-r}{\pi ^{\rho _{\mathfrak{t}}}}$
,
![]() $u_{\mathfrak{t},w}=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \mathfrak{t}} r_{\mathfrak{t},w}$
and
$u_{\mathfrak{t},w}=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \mathfrak{t}} r_{\mathfrak{t},w}$
and
![]() $u_{{\mathfrak{s}}_h,w_h}^0=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \{w_h\}} r_{{\mathfrak{s}}_h,w_h}$
. Define
$u_{{\mathfrak{s}}_h,w_h}^0=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \{w_h\}} r_{{\mathfrak{s}}_h,w_h}$
. Define
![]() ${\overline{f_{\mathfrak{t},w}^W}},{\overline{g_{\mathfrak{t},w}}}\in k[X]$
, and
${\overline{f_{\mathfrak{t},w}^W}},{\overline{g_{\mathfrak{t},w}}}\in k[X]$
, and
![]() ${\overline{g_{{\mathfrak{s}}_h,w_h}^0}}\in k[X]$
for any
${\overline{g_{{\mathfrak{s}}_h,w_h}^0}}\in k[X]$
for any
![]() $h=1,\dots,m$
, as follows:
$h=1,\dots,m$
, as follows:
-
(i) Let
 $u=u_{\mathfrak{t},w}$
. Define
$u=u_{\mathfrak{t},w}$
. Define
 $\overline{f_{\mathfrak{t},w}^W}$
by
where the union runs through all children
$\overline{f_{\mathfrak{t},w}^W}$
by
where the union runs through all children \begin{align*} \overline{f_{\mathfrak{t},w}^W}(X^{b_{\mathfrak{t}}})= \tfrac{u}{\pi ^{v(u)}}\prod _{r\in \mathfrak{t}\setminus \bigcup _{\mathfrak{s}\lt \mathfrak{t}}\mathfrak{s}} (X+r_{\mathfrak{t},w})\mod \pi, \end{align*}
\begin{align*} \overline{f_{\mathfrak{t},w}^W}(X^{b_{\mathfrak{t}}})= \tfrac{u}{\pi ^{v(u)}}\prod _{r\in \mathfrak{t}\setminus \bigcup _{\mathfrak{s}\lt \mathfrak{t}}\mathfrak{s}} (X+r_{\mathfrak{t},w})\mod \pi, \end{align*}
 $\mathfrak{s}$
of
$\mathfrak{s}$
of
 $\mathfrak{t}$
in
$\mathfrak{t}$
in
 $\Sigma ^W$
. If
$\Sigma ^W$
. If
 $\Sigma =\Sigma _C^{\textrm{min}}$
denote
$\Sigma =\Sigma _C^{\textrm{min}}$
denote
 $\overline{f_{\mathfrak{t},w}^W}$
by
$\overline{f_{\mathfrak{t},w}^W}$
by
 $\overline{f_{\mathfrak{t},w}}$
.
$\overline{f_{\mathfrak{t},w}}$
.
-
(ii) Let
 $u=u_{\mathfrak{t},w}$
. Define
$u=u_{\mathfrak{t},w}$
. Define
 $\overline{g_{\mathfrak{t},w}}(X)\;:\!=\; X^{p_{\mathfrak{t}}/\gamma _{\mathfrak{t}}} - \tfrac{u}{\pi ^{v(u)}}\mod \pi$
.
$\overline{g_{\mathfrak{t},w}}(X)\;:\!=\; X^{p_{\mathfrak{t}}/\gamma _{\mathfrak{t}}} - \tfrac{u}{\pi ^{v(u)}}\mod \pi$
. -
(iii) Let
 $u=u_{{\mathfrak{s}}_h,w_h}^0$
. Define
$u=u_{{\mathfrak{s}}_h,w_h}^0$
. Define
 $\overline{g_{{\mathfrak{s}}_h,w_h}^0}(X)\;:\!=\;X^{p_{{\mathfrak{s}}_h}^0/\gamma _{{\mathfrak{s}}_h}^0} - \tfrac{u}{\pi ^{v(u)}}\mod \pi$
.
$\overline{g_{{\mathfrak{s}}_h,w_h}^0}(X)\;:\!=\;X^{p_{{\mathfrak{s}}_h}^0/\gamma _{{\mathfrak{s}}_h}^0} - \tfrac{u}{\pi ^{v(u)}}\mod \pi$
.
Note that the polynomials defined in Definition 5.12 agree with the ones in Definition 4.14 when
![]() $w=w_{\mathfrak{t}}$
.
$w=w_{\mathfrak{t}}$
.
Lemma 5.13.
Let
![]() $\mathfrak{s},\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
, with
$\mathfrak{s},\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
, with
![]() $\mathfrak{s}\subsetneq \mathfrak{t}$
. Let
$\mathfrak{s}\subsetneq \mathfrak{t}$
. Let
![]() $w',w$
be rational centres of
$w',w$
be rational centres of
![]() $\mathfrak{s}$
and
$\mathfrak{s}$
and
![]() $\mathfrak{t}$
respectively, and define
$\mathfrak{t}$
respectively, and define
![]() ${\overline{u_{w'w}}}=\tfrac{w'-w}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
. Then
${\overline{u_{w'w}}}=\tfrac{w'-w}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
. Then
![]() $\overline{u_{w'w}}$
does not depend on the choice of a rational centre
$\overline{u_{w'w}}$
does not depend on the choice of a rational centre
![]() $w'$
of
$w'$
of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
Proof. Suppose that
![]() $w_1,w_2$
are two rational centres of
$w_1,w_2$
are two rational centres of
![]() $\mathfrak{s}$
. Then
$\mathfrak{s}$
. Then
![]() $v(w_1-w_2)\geq \rho _{\mathfrak{s}}\gt \rho _{\mathfrak{t}}$
, and so the Lemma follows.
$v(w_1-w_2)\geq \rho _{\mathfrak{s}}\gt \rho _{\mathfrak{t}}$
, and so the Lemma follows.
Remark 5.14.
Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
. Let
$\mathfrak{t}\in \Sigma _C^{w_h}$
. Let
![]() $l=1,\dots,m$
,
$l=1,\dots,m$
,
![]() $l\neq h$
. Then
$l\neq h$
. Then
![]() $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
if and only if it has a child
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
if and only if it has a child
![]() $\mathfrak{s}\in \Sigma _C^{w_l}\setminus \Sigma _C^{w_h}$
. In particular, if this happens, Lemma 5.13 shows that
$\mathfrak{s}\in \Sigma _C^{w_l}\setminus \Sigma _C^{w_h}$
. In particular, if this happens, Lemma 5.13 shows that
![]() $\overline{u_{lh}}=\frac{w-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
for any rational centre
$\overline{u_{lh}}=\frac{w-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
for any rational centre
![]() $w$
of
$w$
of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
Definition 5.15.
Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Define
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Define
![]() $\hat{\mathfrak{t}}^W\;:\!=\;\{\mathfrak{s}\in \Sigma ^W\cup \{\varnothing \}\mid \mathfrak{s}\lt \mathfrak{t}\}$
, where
$\hat{\mathfrak{t}}^W\;:\!=\;\{\mathfrak{s}\in \Sigma ^W\cup \{\varnothing \}\mid \mathfrak{s}\lt \mathfrak{t}\}$
, where
![]() $\varnothing \lt \mathfrak{t}$
only if
$\varnothing \lt \mathfrak{t}$
only if
![]() $\mathfrak{t}$
has no child in
$\mathfrak{t}$
has no child in
![]() $\Sigma ^W$
. If
$\Sigma ^W$
. If
![]() $\varnothing \lt \mathfrak{t}$
then we will say that
$\varnothing \lt \mathfrak{t}$
then we will say that
![]() $w_h$
is the rational centre of
$w_h$
is the rational centre of
![]() $\varnothing$
.
$\varnothing$
.
Define
![]() ${\mathbb{G}}_{\mathfrak{t},w_h}\;:\!=\;{\mathbb{G}}_{m,k}\setminus \bigcup _l\{{\overline{u_{lh}}}\}$
, where the union runs through all
${\mathbb{G}}_{\mathfrak{t},w_h}\;:\!=\;{\mathbb{G}}_{m,k}\setminus \bigcup _l\{{\overline{u_{lh}}}\}$
, where the union runs through all
![]() $l\neq h$
such that
$l\neq h$
such that
![]() ${\mathfrak{s}}_l\wedge{\mathfrak{s}}_h=\mathfrak{t}$
. Note that Remark 5.14 shows that
${\mathfrak{s}}_l\wedge{\mathfrak{s}}_h=\mathfrak{t}$
. Note that Remark 5.14 shows that
![]() ${\mathbb{G}}_{\mathfrak{t},w_h}={\mathbb{A}}_k^1\setminus \bigcup _{\mathfrak{s}\in \hat{\mathfrak{t}}^W}\{{\overline{u_{w_{\mathfrak{s}} w_h}}}\}$
, where
${\mathbb{G}}_{\mathfrak{t},w_h}={\mathbb{A}}_k^1\setminus \bigcup _{\mathfrak{s}\in \hat{\mathfrak{t}}^W}\{{\overline{u_{w_{\mathfrak{s}} w_h}}}\}$
, where
![]() ${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
![]() $w_{\mathfrak{s}}$
is any rational centre of
$w_{\mathfrak{s}}$
is any rational centre of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Let
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Let
![]() $V=V_{\mathfrak{t}}^{w_h}$
and
$V=V_{\mathfrak{t}}^{w_h}$
and
![]() $M=M_{V,j}$
. In Section 5.5 we showed the special fibre of
$M=M_{V,j}$
. In Section 5.5 we showed the special fibre of
![]() $U^h_M$
equals
$U^h_M$
equals
![]() $X_M\cap \mathcal{C}_{\Delta,s}^{w_h}$
. Therefore the components of
$X_M\cap \mathcal{C}_{\Delta,s}^{w_h}$
. Therefore the components of
![]() $\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
coming from
$\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
coming from
![]() $V$
are the same of those of
$V$
are the same of those of
![]() $\mathcal{C}_{\Delta,s}^{w_h}$
given by the same
$\mathcal{C}_{\Delta,s}^{w_h}$
given by the same
![]() $v$
-edge. Therefore
$v$
-edge. Therefore
![]() $V$
gives a closed subscheme
$V$
gives a closed subscheme
![]() $X_V\times{\mathbb{P}}_V$
of
$X_V\times{\mathbb{P}}_V$
of
![]() $\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
, where
$\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
, where
![]() ${\mathbb{P}}_V$
is a chain of
${\mathbb{P}}_V$
is a chain of
![]() ${\mathbb{P}}_k^1$
s and
${\mathbb{P}}_k^1$
s and
![]() $X_V\;:\;\{\overline{g_h|_{V}}=0\}$
over
$X_V\;:\;\{\overline{g_h|_{V}}=0\}$
over
![]() ${\mathbb{G}}_{m,k}$
. Lemma 4.3 implies that
${\mathbb{G}}_{m,k}$
. Lemma 4.3 implies that
![]() $\overline{g_h|_{V}}=\overline{g_{\mathfrak{t},w_h}}$
.
$\overline{g_h|_{V}}=\overline{g_{\mathfrak{t},w_h}}$
.
Let
![]() $V_0=V_0^{w_h}$
and
$V_0=V_0^{w_h}$
and
![]() $M=M_{V_0,j}$
. Similarly to above,
$M=M_{V_0,j}$
. Similarly to above,
![]() $X_M\cap\mathring{\mathcal{C}}_{\Delta,s}^{w_h}=X_M\cap \mathcal{C}_{\Delta,s}^{w_h}$
and so
$X_M\cap\mathring{\mathcal{C}}_{\Delta,s}^{w_h}=X_M\cap \mathcal{C}_{\Delta,s}^{w_h}$
and so
![]() $V_0$
gives rise to a closed subscheme
$V_0$
gives rise to a closed subscheme
![]() $X_{V_0}\times{\mathbb{P}}_{V_0}$
of
$X_{V_0}\times{\mathbb{P}}_{V_0}$
of
![]() $\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
, where
$\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
, where
![]() ${\mathbb{P}}_{V_0}$
is a chain of
${\mathbb{P}}_{V_0}$
is a chain of
![]() ${\mathbb{P}}_k^1$
s and
${\mathbb{P}}_k^1$
s and
![]() $X_{V_0}\;:\;\{\overline{g_h|_{V_0}}=0\}$
over
$X_{V_0}\;:\;\{\overline{g_h|_{V_0}}=0\}$
over
![]() ${\mathbb{G}}_{m,k}$
. Note that
${\mathbb{G}}_{m,k}$
. Note that
![]() $\overline{g_h|_{V_0}}=\overline{g_{{\mathfrak{s}}_h,w_h}^0}$
.
$\overline{g_h|_{V_0}}=\overline{g_{{\mathfrak{s}}_h,w_h}^0}$
.
Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Let
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. Let
![]() $L=L_{\mathfrak{t}}^{w_h}$
and
$L=L_{\mathfrak{t}}^{w_h}$
and
![]() $M=M_{L,i}$
. By Lemma 5.8, the
$M=M_{L,i}$
. By Lemma 5.8, the
![]() $v$
-edge
$v$
-edge
![]() $L$
gives a subscheme
$L$
gives a subscheme
![]() $X_{L}^W\times{\mathbb{P}}_{L}$
of
$X_{L}^W\times{\mathbb{P}}_{L}$
of
![]() $\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
, where
$\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
, where
![]() ${\mathbb{P}}_{L}$
is a chain of
${\mathbb{P}}_{L}$
is a chain of
![]() ${\mathbb{P}}_k^1$
s of length
${\mathbb{P}}_k^1$
s of length
![]() $r_L$
and
$r_L$
and
![]() $X_L^W\;:\;\{\overline{g_h|_{L}}=0\}$
in
$X_L^W\;:\;\{\overline{g_h|_{L}}=0\}$
in
![]() ${\mathbb{G}}_{\mathfrak{t},w_h}$
. Note that
${\mathbb{G}}_{\mathfrak{t},w_h}$
. Note that
![]() $r_L=0$
or
$r_L=0$
or
![]() $1$
by Lemma 4.3 and
$1$
by Lemma 4.3 and
![]() $r_L=1$
if and only if
$r_L=1$
if and only if
![]() $D_{\mathfrak{t}}=1$
. Let
$D_{\mathfrak{t}}=1$
. Let
![]() $\mathfrak{t}_h\in \Sigma _C^{w_h}$
be the unique child of
$\mathfrak{t}_h\in \Sigma _C^{w_h}$
be the unique child of
![]() $\mathfrak{t}$
with rational centre
$\mathfrak{t}$
with rational centre
![]() $w_h$
or set
$w_h$
or set
![]() $\mathfrak{t}_h=\varnothing$
if
$\mathfrak{t}_h=\varnothing$
if
![]() $\mathfrak{t}$
has no such child. We will show that
$\mathfrak{t}$
has no such child. We will show that
where
![]() ${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
![]() $w_{\mathfrak{s}}$
is any rational centre of
$w_{\mathfrak{s}}$
is any rational centre of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
Suppose
![]() $\mathfrak{t}\neq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
for any
$\mathfrak{t}\neq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
for any
![]() $l\neq h$
. Equivalently, all children of
$l\neq h$
. Equivalently, all children of
![]() $\mathfrak{t}$
in
$\mathfrak{t}$
in
![]() $\Sigma ^W$
(at most one) belong to
$\Sigma ^W$
(at most one) belong to
![]() $\Sigma _C^{w_h}$
. Then Lemma 4.3 shows that
$\Sigma _C^{w_h}$
. Then Lemma 4.3 shows that
![]() $\overline{g_h|_{L}}=-\overline{f_{\mathfrak{t},w_h}^W}$
. Suppose now that
$\overline{g_h|_{L}}=-\overline{f_{\mathfrak{t},w_h}^W}$
. Suppose now that
![]() $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
for some
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
for some
![]() $l\neq h$
. In this case
$l\neq h$
. In this case
![]() $b_{\mathfrak{t}}=1$
. We have
$b_{\mathfrak{t}}=1$
. We have
where
![]() $r_{\mathfrak{t},w_h}$
and
$r_{\mathfrak{t},w_h}$
and
![]() $u=u_{\mathfrak{t},w_h}$
are as in Definition 5.12. Indeed,
$u=u_{\mathfrak{t},w_h}$
are as in Definition 5.12. Indeed,
![]() $\overline{u_{w_{\mathfrak{s}} w_h}}= r_{\mathfrak{t},w_h}\mod \pi$
for every
$\overline{u_{w_{\mathfrak{s}} w_h}}= r_{\mathfrak{t},w_h}\mod \pi$
for every
![]() $r\in \mathfrak{s}$
as
$r\in \mathfrak{s}$
as
![]() $v(w_{\mathfrak{s}}-r)\geq \rho _{\mathfrak{s}}\gt \rho _{\mathfrak{t}}$
, and since
$v(w_{\mathfrak{s}}-r)\geq \rho _{\mathfrak{s}}\gt \rho _{\mathfrak{t}}$
, and since
![]() $b_{\mathfrak{t}}=1$
, Lemma 4.3 implies that
$b_{\mathfrak{t}}=1$
, Lemma 4.3 implies that
In particular, Remark 5.13 and Lemma 5.9 shows that
![]() $(X+{\overline{u_{hl}}})\nmid{\overline{f_{\mathfrak{t},w_h}^W}}(X)$
, for any
$(X+{\overline{u_{hl}}})\nmid{\overline{f_{\mathfrak{t},w_h}^W}}(X)$
, for any
![]() $l\neq h$
such that
$l\neq h$
such that
![]() ${\mathfrak{s}}_l\wedge{\mathfrak{s}}_h=\mathfrak{t}$
. Moreover,
${\mathfrak{s}}_l\wedge{\mathfrak{s}}_h=\mathfrak{t}$
. Moreover,
![]() $X\nmid{\overline{f_{\mathfrak{t},w_h}^W}}(X)$
by definition. Therefore the scheme
$X\nmid{\overline{f_{\mathfrak{t},w_h}^W}}(X)$
by definition. Therefore the scheme
![]() $X_L^W$
is equal to the closed subscheme
$X_L^W$
is equal to the closed subscheme
![]() $X_{\mathfrak{t},w_h}^W\subset{\mathbb{A}}_{k}^1$
given by
$X_{\mathfrak{t},w_h}^W\subset{\mathbb{A}}_{k}^1$
given by
![]() ${\overline{f_{\mathfrak{t},w_h}^W}}=0$
.
${\overline{f_{\mathfrak{t},w_h}^W}}=0$
.
Let
![]() $\mathfrak{t}\in \Sigma ^W$
be a proper cluster. For any
$\mathfrak{t}\in \Sigma ^W$
be a proper cluster. For any
![]() $h=1,\dots,m$
such that
$h=1,\dots,m$
such that
![]() ${\mathfrak{s}}_h\subseteq \mathfrak{t}$
, let
${\mathfrak{s}}_h\subseteq \mathfrak{t}$
, let
![]() $\bar{X}_{F_{\mathfrak{t}}^{w_h}}$
be the
$\bar{X}_{F_{\mathfrak{t}}^{w_h}}$
be the
![]() $1$
-dimensional closed subscheme of
$1$
-dimensional closed subscheme of
![]() $\mathcal{C}_{\Delta,s}^{w_h}$
given by
$\mathcal{C}_{\Delta,s}^{w_h}$
given by
![]() $F_{\mathfrak{t}}^{w_h}$
. Define
$F_{\mathfrak{t}}^{w_h}$
. Define
Denote by
![]() $\Gamma _{\mathfrak{t}}$
the
$\Gamma _{\mathfrak{t}}$
the
![]() $1$
-dimensional closed subscheme of
$1$
-dimensional closed subscheme of
![]() $\mathcal{C}_s$
, result of the glueing of the subschemes
$\mathcal{C}_s$
, result of the glueing of the subschemes
![]() $\mathring{X}_{F_{\mathfrak{t}}^{w_h}}$
of
$\mathring{X}_{F_{\mathfrak{t}}^{w_h}}$
of
![]() $\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
to varying of
$\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
to varying of
![]() $h$
such that
$h$
such that
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
.
$\mathfrak{t}\in \Sigma _C^{w_h}$
.
Lemma 5.16.
Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. The multiplicity of
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster. The multiplicity of
![]() $\Gamma _{\mathfrak{t}}$
in
$\Gamma _{\mathfrak{t}}$
in
![]() $\mathcal{C}_s$
is
$\mathcal{C}_s$
is
![]() $m_{\mathfrak{t}}$
.
$m_{\mathfrak{t}}$
.
Proof. Let
![]() $L=L_{\mathfrak{t}}^{w_h}$
,
$L=L_{\mathfrak{t}}^{w_h}$
,
![]() $M=M_{L,0}$
, and let
$M=M_{L,0}$
, and let
![]() $F=F_{\mathfrak{t}}^{w_h}$
. The multiplicity of
$F=F_{\mathfrak{t}}^{w_h}$
. The multiplicity of
![]() $\bar{X}_{F_{\mathfrak{t}}^{w_h}}$
, and so of
$\bar{X}_{F_{\mathfrak{t}}^{w_h}}$
, and so of
![]() $ X_{F_{\mathfrak{t}}^{w_h}}$
and
$ X_{F_{\mathfrak{t}}^{w_h}}$
and
![]() $\Gamma _{\mathfrak{t}}$
, is
$\Gamma _{\mathfrak{t}}$
, is
![]() $\delta _F$
. Hence we only need to show that
$\delta _F$
. Hence we only need to show that
![]() $m_{\mathfrak{t}}=\delta _F$
. Let
$m_{\mathfrak{t}}=\delta _F$
. Let
![]() $d_0\in \mathbb{Z}$
as in Lemma 5.2. Then
$d_0\in \mathbb{Z}$
as in Lemma 5.2. Then
![]() $\delta _F=\delta _L d_0$
. The result follows as
$\delta _F=\delta _L d_0$
. The result follows as
![]() $\delta _L=b_{\mathfrak{t}}$
and
$\delta _L=b_{\mathfrak{t}}$
and
![]() $d_0$
, denominator of
$d_0$
, denominator of
![]() $s_1^L$
, equals
$s_1^L$
, equals
![]() $3-D_{\mathfrak{t}}$
by Lemma 4.3.
$3-D_{\mathfrak{t}}$
by Lemma 4.3.
Lemma 5.17.
Let
![]() $L=L_{\mathfrak{t}}^{w_h}$
,
$L=L_{\mathfrak{t}}^{w_h}$
,
![]() $F=F_{\mathfrak{t}}^{w_h}$
and
$F=F_{\mathfrak{t}}^{w_h}$
and
![]() $M=M_{L,0}$
. Let
$M=M_{L,0}$
. Let
![]() $c\in \{0,\dots,b_{\mathfrak{t}}-1\}$
such that
$c\in \{0,\dots,b_{\mathfrak{t}}-1\}$
such that
![]() $1/b_{\mathfrak{t}}-\rho _{\mathfrak{t}}\cdot c\in \mathbb{Z}$
. Then
$1/b_{\mathfrak{t}}-\rho _{\mathfrak{t}}\cdot c\in \mathbb{Z}$
. Then
![]() $\mathcal{F}_M^h(X,Y,0)\mod \pi$
equals the polynomial
$\mathcal{F}_M^h(X,Y,0)\mod \pi$
equals the polynomial
where
![]() ${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
![]() $w_{\mathfrak{s}}$
is any rational centre of
$w_{\mathfrak{s}}$
is any rational centre of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
In particular,
![]() $\Gamma _{\mathfrak{t}}^h\subset{\mathbb{G}}_{\mathfrak{t},w_h}\times{\mathbb{A}}_k^1$
given by
$\Gamma _{\mathfrak{t}}^h\subset{\mathbb{G}}_{\mathfrak{t},w_h}\times{\mathbb{A}}_k^1$
given by
![]() ${\overline{g|_F}}=0$
is the open subscheme
${\overline{g|_F}}=0$
is the open subscheme
![]() $U_M^h\cap \{Z=0\}$
of
$U_M^h\cap \{Z=0\}$
of
![]() $\mathring{X}_F$
, and the points in
$\mathring{X}_F$
, and the points in
![]() $S_M$
belong to all irreducible components of
$S_M$
belong to all irreducible components of
![]() $\bar{X}_{F}$
.
$\bar{X}_{F}$
.
Proof. From [Reference Dokchitser1, §3.5] and the equation of
![]() $C^{w_h}$
, the polynomial
$C^{w_h}$
, the polynomial
![]() $\mathcal{F}_M^h(X,Y,0)$
reduces modulo
$\mathcal{F}_M^h(X,Y,0)$
reduces modulo
![]() $\pi$
to
$\pi$
to
![]() $X^{a_1}Y^b+X^{a_2}{\overline{g_h|_{L}}}(X)$
, for some
$X^{a_1}Y^b+X^{a_2}{\overline{g_h|_{L}}}(X)$
, for some
![]() $b=1,2$
and
$b=1,2$
and
![]() $a\in \mathbb{Z}$
. Lemma 4.9 shows that
$a\in \mathbb{Z}$
. Lemma 4.9 shows that
![]() $b=D_{\mathfrak{t}}$
. By Lemma 4.3,
$b=D_{\mathfrak{t}}$
. By Lemma 4.3,
![]() $a_1=2\tilde{m}_{12}$
,
$a_1=2\tilde{m}_{12}$
,
![]() $a_2=|\mathfrak{t}_h|\tilde{m}_{11}+(\epsilon _{\mathfrak{t}}-|\mathfrak{t}_h|\rho _{\mathfrak{t}})\tilde{m}_{13}$
, where
$a_2=|\mathfrak{t}_h|\tilde{m}_{11}+(\epsilon _{\mathfrak{t}}-|\mathfrak{t}_h|\rho _{\mathfrak{t}})\tilde{m}_{13}$
, where
![]() $\mathfrak{t}_h\in \Sigma _C^{w_h}\cup \{\varnothing \}$
,
$\mathfrak{t}_h\in \Sigma _C^{w_h}\cup \{\varnothing \}$
,
![]() $\mathfrak{t}_h\lt \mathfrak{t}$
. Then
$\mathfrak{t}_h\lt \mathfrak{t}$
. Then
![]() $a_1=0$
and
$a_1=0$
and
![]() $a_2=\tfrac{|\mathfrak{t}_h|}{b_{\mathfrak{t}}}-c\epsilon _{\mathfrak{t}}$
by Lemma 5.2.
$a_2=\tfrac{|\mathfrak{t}_h|}{b_{\mathfrak{t}}}-c\epsilon _{\mathfrak{t}}$
by Lemma 5.2.
If
![]() $\mathfrak{t}$
has one or no child, or
$\mathfrak{t}$
has one or no child, or
![]() $D_{\mathfrak{t}}=1$
, then
$D_{\mathfrak{t}}=1$
, then
![]() ${\overline{g_h|_L}}=-{\overline{f_{\mathfrak{t},w_h}^W}}$
by (7). On the other hand, if
${\overline{g_h|_L}}=-{\overline{f_{\mathfrak{t},w_h}^W}}$
by (7). On the other hand, if
![]() $D_{\mathfrak{t}}=2$
and
$D_{\mathfrak{t}}=2$
and
![]() $\mathfrak{t}$
has two or more children in
$\mathfrak{t}$
has two or more children in
![]() $\Sigma _C^{\textrm{rat}}$
, then
$\Sigma _C^{\textrm{rat}}$
, then
![]() $b_{\mathfrak{t}}=1$
, and so
$b_{\mathfrak{t}}=1$
, and so
![]() $c=0$
. Therefore the equality (7) concludes the proof of the first part of the statement also in this case. Finally, the last part of the Lemma follows from Lemma 5.8.
$c=0$
. Therefore the equality (7) concludes the proof of the first part of the statement also in this case. Finally, the last part of the Lemma follows from Lemma 5.8.
Let
![]() $c$
as in the previous Lemma and define
$c$
as in the previous Lemma and define
![]() $\tilde{\mathfrak{t}}^W\;:\!=\;\{\mathfrak{s}\in \hat{\mathfrak{t}}^W\mid \frac{|\mathfrak{s}|}{b_{\mathfrak{t}}}-c\epsilon _{\mathfrak{t}}\notin 2\mathbb{Z}\}$
.
$\tilde{\mathfrak{t}}^W\;:\!=\;\{\mathfrak{s}\in \hat{\mathfrak{t}}^W\mid \frac{|\mathfrak{s}|}{b_{\mathfrak{t}}}-c\epsilon _{\mathfrak{t}}\notin 2\mathbb{Z}\}$
.
Proposition 5.18.
Let
![]() $L=L_{\mathfrak{t}}^{w_h}$
and
$L=L_{\mathfrak{t}}^{w_h}$
and
![]() $M=M_{L,0}$
. The dense open subscheme
$M=M_{L,0}$
. The dense open subscheme
![]() $\Gamma _{\mathfrak{t}}\cap U_M^h$
of
$\Gamma _{\mathfrak{t}}\cap U_M^h$
of
![]() $\Gamma _{\mathfrak{t}}$
is isomorphic to the closed subscheme of
$\Gamma _{\mathfrak{t}}$
is isomorphic to the closed subscheme of
![]() ${\mathbb{G}}_{\mathfrak{t},w_h}\times{\mathbb{A}}^1_k$
given by
${\mathbb{G}}_{\mathfrak{t},w_h}\times{\mathbb{A}}^1_k$
given by
where
![]() ${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
![]() $w_{\mathfrak{s}}$
is any rational centre of
$w_{\mathfrak{s}}$
is any rational centre of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
Proof. The proposition follows from Lemma 5.17 and the definition of
![]() ${\mathbb{G}}_{\mathfrak{t},w_h}$
.
${\mathbb{G}}_{\mathfrak{t},w_h}$
.
We conclude this subsection describing how the glueing morphism (4) restricts to the special fibre. Suppose
![]() $\mathfrak{t}\supseteq{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
for
$\mathfrak{t}\supseteq{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
for
![]() $l\neq h$
and let
$l\neq h$
and let
![]() $M$
be a matrix associated to
$M$
be a matrix associated to
![]() $\mathfrak{t}$
. Consider the glueing map
$\mathfrak{t}$
. Consider the glueing map
![]() $U_M^h\rightarrow U_M^l$
explicitly defined in Section 5.3.
$U_M^h\rightarrow U_M^l$
explicitly defined in Section 5.3.
Suppose first
![]() $M=M_{V,j}$
with
$M=M_{V,j}$
with
![]() $V=V_{\mathfrak{t}}^{w_l}$
. By Lemma 5.10 the glueing morphism restricts to the identity on
$V=V_{\mathfrak{t}}^{w_l}$
. By Lemma 5.10 the glueing morphism restricts to the identity on
![]() $X_V\times{\mathbb{P}}_V$
.
$X_V\times{\mathbb{P}}_V$
.
Suppose
![]() $M=M_{L,i}$
with
$M=M_{L,i}$
with
![]() $L=L_{\mathfrak{t}}^{w_l}$
. Note that
$L=L_{\mathfrak{t}}^{w_l}$
. Note that
![]() $\tilde{m}_{12}=0$
from Lemma 5.2. Recall the open subscheme
$\tilde{m}_{12}=0$
from Lemma 5.2. Recall the open subscheme
![]() $\Gamma _{\mathfrak{t}}^h$
of
$\Gamma _{\mathfrak{t}}^h$
of
![]() $ X_{F_{\mathfrak{t}}^{w_h}}$
defined in Lemma 5.17. Then, Lemma 5.7 implies that the glueing map restricts to an isomorphism
$ X_{F_{\mathfrak{t}}^{w_h}}$
defined in Lemma 5.17. Then, Lemma 5.7 implies that the glueing map restricts to an isomorphism
![]() $\Gamma _{\mathfrak{t}}^h\mapsto \Gamma _{\mathfrak{t}}^l$
induced by the ring homomorphism sending
$\Gamma _{\mathfrak{t}}^h\mapsto \Gamma _{\mathfrak{t}}^l$
induced by the ring homomorphism sending
![]() $X\mapsto X+{\overline{u_{w_hw_l}}}$
, where
$X\mapsto X+{\overline{u_{w_hw_l}}}$
, where
![]() ${\overline{u_{w_hw_l}}}=\tfrac{w_h-w_l}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
. Similarly, it restricts to an isomorphism
${\overline{u_{w_hw_l}}}=\tfrac{w_h-w_l}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
. Similarly, it restricts to an isomorphism
![]() $X_{L_{\mathfrak{t}}^{w_h}}^W\times{\mathbb{P}}_{L_{\mathfrak{t}}^{w_h}}\rightarrow X_{L_{\mathfrak{t}}^{w_l}}^W\times{\mathbb{P}}_{L_{\mathfrak{t}}^{w_l}}$
, where
$X_{L_{\mathfrak{t}}^{w_h}}^W\times{\mathbb{P}}_{L_{\mathfrak{t}}^{w_h}}\rightarrow X_{L_{\mathfrak{t}}^{w_l}}^W\times{\mathbb{P}}_{L_{\mathfrak{t}}^{w_l}}$
, where
![]() ${\mathbb{P}}_{L_{\mathfrak{t}}^{w_h}}\rightarrow{\mathbb{P}}_{L_{\mathfrak{t}}^{w_l}}$
is the identity and
${\mathbb{P}}_{L_{\mathfrak{t}}^{w_h}}\rightarrow{\mathbb{P}}_{L_{\mathfrak{t}}^{w_l}}$
is the identity and
![]() $X_{L_{\mathfrak{t}}^{w_h}}^W\rightarrow X_{L_{\mathfrak{t}}^{w_l}}^W$
is induced by the ring homomorphism sending
$X_{L_{\mathfrak{t}}^{w_h}}^W\rightarrow X_{L_{\mathfrak{t}}^{w_l}}^W$
is induced by the ring homomorphism sending
![]() $X\mapsto X+{\overline{u_{w_hw_l}}}$
.
$X\mapsto X+{\overline{u_{w_hw_l}}}$
.
5.7. Regularity
Let
![]() $w_h\in W$
. We want to show that if
$w_h\in W$
. We want to show that if
![]() $\Sigma =\Sigma _C^{\textrm{min}}$
, and
$\Sigma =\Sigma _C^{\textrm{min}}$
, and
![]() $C$
has an almost rational cluster picture and is
$C$
has an almost rational cluster picture and is
![]() $y$
-regular, then
$y$
-regular, then
![]() $\mathring{\mathcal{C}}_{\Delta }^{w_h}$
is a regular scheme.
$\mathring{\mathcal{C}}_{\Delta }^{w_h}$
is a regular scheme.
Lemma 5.19.
Consider the model
![]() $\mathcal{C}_\Delta ^{w_h}/O_K$
and let
$\mathcal{C}_\Delta ^{w_h}/O_K$
and let
![]() $f_h(x)=f(x+w_h)$
. Suppose
$f_h(x)=f(x+w_h)$
. Suppose
![]() $\Sigma =\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}=\Sigma _C^{\textrm{min}}$
, and
$\Sigma =\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}=\Sigma _C^{\textrm{min}}$
, and
![]() $C$
has an almost rational cluster picture and is
$C$
has an almost rational cluster picture and is
![]() $y$
-regular. If
$y$
-regular. If
![]() $P$
is a singular point of
$P$
is a singular point of
![]() $\mathcal{C}_\Delta ^{w_h}$
then
$\mathcal{C}_\Delta ^{w_h}$
then
for some
![]() $l\neq h$
, where
$l\neq h$
, where
![]() $M= M_{L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h},i}$
for
$M= M_{L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h},i}$
for
![]() $i=0,\dots,r_{L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}}$
.
$i=0,\dots,r_{L_{{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l}^{w_h}}$
.
Proof. Denote by
![]() $m_\alpha (X)\in O_K[X]$
a lift of the minimal polynomial in
$m_\alpha (X)\in O_K[X]$
a lift of the minimal polynomial in
![]() $k[X]$
of
$k[X]$
of
![]() $\bar \alpha \in \bar{k}$
. By Lemma 5.9, we only need to show that if
$\bar \alpha \in \bar{k}$
. By Lemma 5.9, we only need to show that if
![]() $P\in \mathcal{C}_\Delta ^{w_h}$
is a singular point then
$P\in \mathcal{C}_\Delta ^{w_h}$
is a singular point then
for some
![]() $v$
-edge
$v$
-edge
![]() $L=L_{\mathfrak{t}}^{w_h}$
of
$L=L_{\mathfrak{t}}^{w_h}$
of
![]() $\Delta ^{w_h}$
, and some multiple root
$\Delta ^{w_h}$
, and some multiple root
![]() $\bar{\alpha }$
of
$\bar{\alpha }$
of
![]() $\overline{f_h|_L}$
. We study the polynomial
$\overline{f_h|_L}$
. We study the polynomial
![]() $\mathcal{F}_M^h$
to varying of the matrix
$\mathcal{F}_M^h$
to varying of the matrix
![]() $M$
, using [Reference Dokchitser1, §4.5]. Let
$M$
, using [Reference Dokchitser1, §4.5]. Let
![]() $g_h(x,y)=y^2-f_h(x)$
. Let
$g_h(x,y)=y^2-f_h(x)$
. Let
![]() $L=L_{\mathfrak{t}}^{w_h}$
and
$L=L_{\mathfrak{t}}^{w_h}$
and
![]() $M=M_{L,i}$
. Note that
$M=M_{L,i}$
. Note that
![]() ${\overline{g_h|_L}}=-{\overline{f_h|_L}}$
. We have
${\overline{g_h|_L}}=-{\overline{f_h|_L}}$
. We have
![]() $\mathcal{F}_M^h(X,0,Z)={\overline{g_h|_L}}(X)$
for any
$\mathcal{F}_M^h(X,0,Z)={\overline{g_h|_L}}(X)$
for any
![]() $i$
. On the other hand,
$i$
. On the other hand,
![]() $\mathcal{F}_M^h(X,Y,0)={\overline{g_h|_L}}(X)$
if
$\mathcal{F}_M^h(X,Y,0)={\overline{g_h|_L}}(X)$
if
![]() $i\gt 0$
and
$i\gt 0$
and
![]() $\mathcal{F}_M^h(X,Y,0)={\overline{g_h|_F}}(X,Y)$
if
$\mathcal{F}_M^h(X,Y,0)={\overline{g_h|_F}}(X,Y)$
if
![]() $i=0$
. From the description given in Lemma 5.17, we conclude that for these matrices
$i=0$
. From the description given in Lemma 5.17, we conclude that for these matrices
![]() $M$
the points in (8) are the only possibly singular points of
$M$
the points in (8) are the only possibly singular points of
![]() $\mathcal{C}_{\Delta }^{w_h}\cap X_M$
. In particular, this proves that for any
$\mathcal{C}_{\Delta }^{w_h}\cap X_M$
. In particular, this proves that for any
![]() $v$
-face
$v$
-face
![]() $F$
of
$F$
of
![]() $\Delta ^{w_h}$
, the points in
$\Delta ^{w_h}$
, the points in
![]() $X_F$
are non-singular in
$X_F$
are non-singular in
![]() $\mathcal{C}_{\Delta }^{w_h}$
.
$\mathcal{C}_{\Delta }^{w_h}$
.
Let
![]() $V=V_{\mathfrak{t}}^{w_h}$
or
$V=V_{\mathfrak{t}}^{w_h}$
or
![]() $V=V_0^{w_h}$
and
$V=V_0^{w_h}$
and
![]() $M=M_{V,j}$
. Since
$M=M_{V,j}$
. Since
![]() $C$
is
$C$
is
![]() $y$
-regular,
$y$
-regular,
![]() $p\nmid \deg ({\overline{g_h|_V}})$
by Lemma 4.9. By [Reference Dokchitser1, §4.5] and the fact that the points in
$p\nmid \deg ({\overline{g_h|_V}})$
by Lemma 4.9. By [Reference Dokchitser1, §4.5] and the fact that the points in
![]() $X_F$
are non-singular for all
$X_F$
are non-singular for all
![]() $v$
-faces
$v$
-faces
![]() $F$
, we conclude that
$F$
, we conclude that
![]() $\mathcal{C}_\Delta ^{w_h}$
has no singular point on
$\mathcal{C}_\Delta ^{w_h}$
has no singular point on
![]() $X_M$
for these matrices
$X_M$
for these matrices
![]() $M$
, as required.
$M$
, as required.
Proposition 5.20.
Suppose
![]() $\Sigma =\Sigma _C^{\textrm{min}}$
, and
$\Sigma =\Sigma _C^{\textrm{min}}$
, and
![]() $C$
has an almost rational cluster picture and is
$C$
has an almost rational cluster picture and is
![]() $y$
-regular, then
$y$
-regular, then
![]() $\mathcal{C}$
is a regular scheme.
$\mathcal{C}$
is a regular scheme.
Proof. Lemmas 5.19 and 5.8 show that
![]() $\mathring{\mathcal{C}}_{\Delta }^{w_h}$
is regular for every
$\mathring{\mathcal{C}}_{\Delta }^{w_h}$
is regular for every
![]() $h$
. Thus their glueing
$h$
. Thus their glueing
![]() $\mathcal{C}$
is regular as well.
$\mathcal{C}$
is regular as well.
5.8. Separatedness
It remains to prove that
![]() $\mathcal{C}$
is a proper scheme. We first show it is separated. Clearly it suffices to prove that
$\mathcal{C}$
is a proper scheme. We first show it is separated. Clearly it suffices to prove that
![]() $\mathcal{X}/O_K$
is separated. Since the schemes
$\mathcal{X}/O_K$
is separated. Since the schemes
![]() $X_\Delta ^h$
are separated, then the open subschemes
$X_\Delta ^h$
are separated, then the open subschemes
![]() $\mathring{X}_\Delta ^{h}$
are separated as well by [Reference Liu9, Proposition 3.3.9]. Consider the open cover
$\mathring{X}_\Delta ^{h}$
are separated as well by [Reference Liu9, Proposition 3.3.9]. Consider the open cover
![]() $\{V_M^h\}_{h,M}$
of
$\{V_M^h\}_{h,M}$
of
![]() $\mathcal{X}$
. Let
$\mathcal{X}$
. Let
![]() $h,l=1,\dots,m$
and let
$h,l=1,\dots,m$
and let
![]() $M_h$
and
$M_h$
and
![]() $M_l$
be matrices associated to proper clusters
$M_l$
be matrices associated to proper clusters
![]() $\mathfrak{t}_h\in \Sigma _C^{w_h}$
and
$\mathfrak{t}_h\in \Sigma _C^{w_h}$
and
![]() $\mathfrak{t}_l\in \Sigma _C^{w_l}$
respectively. By [Reference Liu9, Proposition 3.3.6] we want to show
$\mathfrak{t}_l\in \Sigma _C^{w_l}$
respectively. By [Reference Liu9, Proposition 3.3.6] we want to show
-
(i)
 $V_{M_h}^h\cap V_{M_l}^l$
is affine,
$V_{M_h}^h\cap V_{M_l}^l$
is affine, -
(ii) The canonical homomorphism
is surjective. \begin{align*} O_{\mathcal{X}}(V_{M_h}^h)\otimes _{\mathbb{Z}} O_{\mathcal{X}}(V_{M_l}^l)\longrightarrow O_{\mathcal{X}}(V_{M_h}^h\cap V_{M_l}^l) \end{align*}
\begin{align*} O_{\mathcal{X}}(V_{M_h}^h)\otimes _{\mathbb{Z}} O_{\mathcal{X}}(V_{M_l}^l)\longrightarrow O_{\mathcal{X}}(V_{M_h}^h\cap V_{M_l}^l) \end{align*}
The definition of the glueing map (4) implies (i). If
![]() $h=l$
, or
$h=l$
, or
![]() ${\mathfrak{s}}_l\subseteq \mathfrak{t}_h$
, or
${\mathfrak{s}}_l\subseteq \mathfrak{t}_h$
, or
![]() ${\mathfrak{s}}_h\subseteq \mathfrak{t}_l$
, then (ii) follows from the separatedness of
${\mathfrak{s}}_h\subseteq \mathfrak{t}_l$
, then (ii) follows from the separatedness of
![]() $\mathring{X}_\Delta ^{h}$
and
$\mathring{X}_\Delta ^{h}$
and
![]() $\mathring{X}_\Delta ^{l}$
. So assume
$\mathring{X}_\Delta ^{l}$
. So assume
![]() $l\neq h$
, and
$l\neq h$
, and
![]() $\mathfrak{t}_h,\mathfrak{t}_l\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Consider the Moebius transformation
$\mathfrak{t}_h,\mathfrak{t}_l\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Consider the Moebius transformation
It sends the curve
![]() $C^{w_l}$
to the isomorphic hyperelliptic curve
$C^{w_l}$
to the isomorphic hyperelliptic curve
As
 \begin{align*} f_l^h(x)&\;:\!=\, (xw_{hl}^{-1}+1)^{2g+2}f\left ( x(xw_{hl}^{-1}+1)^{-1}+w_l\right )\\&=c_fw_{hl}^{|\mathfrak{R}|}(xw_{hl}^{-1}+1)^{2g+2-|\mathfrak{R}|}\prod _{r\in \mathfrak{R}\smallsetminus \{w_h\}}\frac{r-w_h}{w_{lh}}\left ( xw_{hl}^{-1}+\frac{r-w_l}{r-w_h}\right ), \end{align*}
\begin{align*} f_l^h(x)&\;:\!=\, (xw_{hl}^{-1}+1)^{2g+2}f\left ( x(xw_{hl}^{-1}+1)^{-1}+w_l\right )\\&=c_fw_{hl}^{|\mathfrak{R}|}(xw_{hl}^{-1}+1)^{2g+2-|\mathfrak{R}|}\prod _{r\in \mathfrak{R}\smallsetminus \{w_h\}}\frac{r-w_h}{w_{lh}}\left ( xw_{hl}^{-1}+\frac{r-w_l}{r-w_h}\right ), \end{align*}
every cluster
![]() $\mathfrak{s}\in \Sigma _C^{w_l}$
such that
$\mathfrak{s}\in \Sigma _C^{w_l}$
such that
![]() $\mathfrak{s}\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, corresponds to a unique cluster
$\mathfrak{s}\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, corresponds to a unique cluster
![]() ${\mathfrak{s}}^h\in \Sigma _{C_l^h}^0$
of same size, same radius and rational centre
${\mathfrak{s}}^h\in \Sigma _{C_l^h}^0$
of same size, same radius and rational centre
![]() $0$
. Moreover,
$0$
. Moreover,
Call
![]() $\mathfrak{t}_l^h$
the cluster in
$\mathfrak{t}_l^h$
the cluster in
![]() $\Sigma _{C_l^h}^0$
corresponding to
$\Sigma _{C_l^h}^0$
corresponding to
![]() $\mathfrak{t}_l$
. Let
$\mathfrak{t}_l$
. Let
![]() $\Delta ^{lh}$
and
$\Delta ^{lh}$
and
![]() $\Delta _v^{lh}$
be the Newton polytopes attached to
$\Delta _v^{lh}$
be the Newton polytopes attached to
![]() $y^2-f_l^h(x)$
and let
$y^2-f_l^h(x)$
and let
![]() $X_\Delta ^{lh}$
be the associated toric scheme (defined in [Reference Dokchitser1, §4.2]). Since
$X_\Delta ^{lh}$
be the associated toric scheme (defined in [Reference Dokchitser1, §4.2]). Since
![]() $\mathfrak{t}_l\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, the
$\mathfrak{t}_l\subsetneq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, the
![]() $v$
-faces
$v$
-faces
![]() $F_{\mathfrak{t}_l}$
of
$F_{\mathfrak{t}_l}$
of
![]() $\Delta ^{w_l}$
and
$\Delta ^{w_l}$
and
![]() $F_{\mathfrak{t}_l^h}$
of
$F_{\mathfrak{t}_l^h}$
of
![]() $\Delta ^{lh}$
are identical by Lemma 4.3. Furthermore, note that if
$\Delta ^{lh}$
are identical by Lemma 4.3. Furthermore, note that if
![]() $\mathfrak{t}_l\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, then
$\mathfrak{t}_l\lt{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
, then
![]() $\rho _{P(\mathfrak{t}_l^h)}\leq \rho _{hl}=\rho _{P(\mathfrak{t}_l)}$
and so
$\rho _{P(\mathfrak{t}_l^h)}\leq \rho _{hl}=\rho _{P(\mathfrak{t}_l)}$
and so
![]() $s_2^{V^0}\leq s_2^{V}$
, where
$s_2^{V^0}\leq s_2^{V}$
, where
![]() $V^0=V_{\mathfrak{t}_l^h}^0$
and
$V^0=V_{\mathfrak{t}_l^h}^0$
and
![]() $V=V_{\mathfrak{t}_l}^{w_l}$
. Therefore the matrix
$V=V_{\mathfrak{t}_l}^{w_l}$
. Therefore the matrix
![]() $M\;:\!=\;M_l$
is also associated to
$M\;:\!=\;M_l$
is also associated to
![]() $\mathfrak{t}_l^h$
.
$\mathfrak{t}_l^h$
.
For every
![]() $o=1,\dots,m$
, with
$o=1,\dots,m$
, with
![]() $o\neq l$
, define
$o\neq l$
, define
 \begin{align*} w_{hlo}=\begin{cases}\dfrac{w_{hl}w_{lo}}{w_{ho}}&\mbox{if } o\neq h,\\ w_{hl}&\mbox{if }o=h,\end{cases} \end{align*}
\begin{align*} w_{hlo}=\begin{cases}\dfrac{w_{hl}w_{lo}}{w_{ho}}&\mbox{if } o\neq h,\\ w_{hl}&\mbox{if }o=h,\end{cases} \end{align*}
and write
![]() $w_{hlo}=u_{hlo}\pi ^{\rho _{hlo}}$
, where
$w_{hlo}=u_{hlo}\pi ^{\rho _{hlo}}$
, where
![]() $u_{hlo}\in O_K^\times$
and
$u_{hlo}\in O_K^\times$
and
![]() $\rho _{hlo}\in \mathbb{Z}$
, i.e.
$\rho _{hlo}\in \mathbb{Z}$
, i.e.
 \begin{align*} u_{hlo}=\begin{cases}\dfrac{u_{hl}u_{lo}}{u_{ho}}&\mbox{if } o\neq h,\\u_{hl}&\mbox{if }o=h,\end{cases}\quad \mbox{ and }\quad \rho _{hlo}=\begin{cases}\rho _{hl}+\rho _{lo}-\rho _{ho}&\mbox{if } o\neq h,\\\rho _{hl}&\mbox{if }o=h.\end{cases} \end{align*}
\begin{align*} u_{hlo}=\begin{cases}\dfrac{u_{hl}u_{lo}}{u_{ho}}&\mbox{if } o\neq h,\\u_{hl}&\mbox{if }o=h,\end{cases}\quad \mbox{ and }\quad \rho _{hlo}=\begin{cases}\rho _{hl}+\rho _{lo}-\rho _{ho}&\mbox{if } o\neq h,\\\rho _{hl}&\mbox{if }o=h.\end{cases} \end{align*}
Define
 \begin{align*} \tilde{T}_M^{hlo}(X,Y,Z)\;:\!=\;\begin{cases}1+u_{hlo}X^{\rho _{hlo}\tilde{m}_{13}-\tilde{m}_{11}}Y^{\rho _{hlo}\tilde{m}_{23}-\tilde{m}_{21}}Z^{\rho _{hlo}\tilde{m}_{33}-\tilde{m}_{31}}&\mbox{if }\mathfrak{t}_l\supseteq{\mathfrak{s}}_o,\\ u_{hlo}^{-1}X^{\tilde{m}_{11}-\rho _{hlo}\tilde{m}_{13}}Y^{\tilde{m}_{21}-\rho _{hlo}\tilde{m}_{23}}Z^{\tilde{m}_{31}-\rho _{hlo}\tilde{m}_{33}}+1&\mbox{if }\mathfrak{t}_l\not \supseteq{\mathfrak{s}}_o. \end{cases} \end{align*}
\begin{align*} \tilde{T}_M^{hlo}(X,Y,Z)\;:\!=\;\begin{cases}1+u_{hlo}X^{\rho _{hlo}\tilde{m}_{13}-\tilde{m}_{11}}Y^{\rho _{hlo}\tilde{m}_{23}-\tilde{m}_{21}}Z^{\rho _{hlo}\tilde{m}_{33}-\tilde{m}_{31}}&\mbox{if }\mathfrak{t}_l\supseteq{\mathfrak{s}}_o,\\ u_{hlo}^{-1}X^{\tilde{m}_{11}-\rho _{hlo}\tilde{m}_{13}}Y^{\tilde{m}_{21}-\rho _{hlo}\tilde{m}_{23}}Z^{\tilde{m}_{31}-\rho _{hlo}\tilde{m}_{33}}+1&\mbox{if }\mathfrak{t}_l\not \supseteq{\mathfrak{s}}_o. \end{cases} \end{align*}
We want to show
![]() $\tilde{T}_M^{hlo}(X,Y,Z)\in R$
. If
$\tilde{T}_M^{hlo}(X,Y,Z)\in R$
. If
![]() $o=h$
then
$o=h$
then
So assume
![]() $o\neq h$
. If
$o\neq h$
. If
![]() ${\mathfrak{s}}_o\subseteq \mathfrak{t}_l$
, then it follows from Lemma 5.4 as
${\mathfrak{s}}_o\subseteq \mathfrak{t}_l$
, then it follows from Lemma 5.4 as
![]() ${\mathfrak{s}}_l\wedge{\mathfrak{s}}_o\subsetneq{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and so
${\mathfrak{s}}_l\wedge{\mathfrak{s}}_o\subsetneq{\mathfrak{s}}_l\wedge{\mathfrak{s}}_h$
and so
![]() $\rho _{hlo}=\rho _{lo}$
. On the other hand, if
$\rho _{hlo}=\rho _{lo}$
. On the other hand, if
![]() ${\mathfrak{s}}_o\not \subseteq \mathfrak{t}_l$
, then it follows from Lemma 5.5 as
${\mathfrak{s}}_o\not \subseteq \mathfrak{t}_l$
, then it follows from Lemma 5.5 as
![]() $\tilde{m}_{23},\tilde{m}_{33}\gt 0$
and
$\tilde{m}_{23},\tilde{m}_{33}\gt 0$
and
![]() $\rho _{hlo}\leq \max \{\rho _{hl},\rho _{lo}\}$
. Let
$\rho _{hlo}\leq \max \{\rho _{hl},\rho _{lo}\}$
. Let
The Moebius transformation
considered above induces an isomorphism
sending
 \begin{align*} X&\mapsto X\cdot T_M^{hl}(X,Y,Z)^{-m_{11}-(g+1) m_{21}},\\ Y&\mapsto Y\cdot T_M^{hl}(X,Y,Z)^{-m_{12}-(g+1) m_{22}},\\ Z&\mapsto Z\cdot T_M^{hl}(X,Y,Z)^{-m_{13}-(g+1) m_{23}}. \end{align*}
\begin{align*} X&\mapsto X\cdot T_M^{hl}(X,Y,Z)^{-m_{11}-(g+1) m_{21}},\\ Y&\mapsto Y\cdot T_M^{hl}(X,Y,Z)^{-m_{12}-(g+1) m_{22}},\\ Z&\mapsto Z\cdot T_M^{hl}(X,Y,Z)^{-m_{13}-(g+1) m_{23}}. \end{align*}
Then
is an open subscheme of
![]() $X_\Delta ^{lh}$
, isomorphic to
$X_\Delta ^{lh}$
, isomorphic to
![]() $V_M^l$
. We can clearly carry out similar constructions for
$V_M^l$
. We can clearly carry out similar constructions for
![]() $t_h$
,
$t_h$
,
![]() $M_h$
.
$M_h$
.
By comparing the Newton polytopes
![]() $\Delta _v^{lh}$
and
$\Delta _v^{lh}$
and
![]() $\Delta _v^{hl}$
, we see that the Moebius transformation
$\Delta _v^{hl}$
, we see that the Moebius transformation
![]() $x\mapsto w_{hl}/(w_{lh}^{-1}x)$
,
$x\mapsto w_{hl}/(w_{lh}^{-1}x)$
,
![]() $y\mapsto y/(w_{lh}^{-1}x)^{g+1}$
gives an isomorphism
$y\mapsto y/(w_{lh}^{-1}x)^{g+1}$
gives an isomorphism
which induces a birational map
![]() $X_\Delta ^{hl}\dashrightarrow X_\Delta ^{lh}$
, defined on the open set
$X_\Delta ^{hl}\dashrightarrow X_\Delta ^{lh}$
, defined on the open set
![]() $\tilde{V}_{M_h}^{hl}$
of
$\tilde{V}_{M_h}^{hl}$
of
![]() $X_\Delta ^{hl}$
. In particular, there exists an open set
$X_\Delta ^{hl}$
. In particular, there exists an open set
![]() $\tilde{V}_{M_h}^{lh}$
of
$\tilde{V}_{M_h}^{lh}$
of
![]() $X_\Delta ^{lh}$
, isomorphic to
$X_\Delta ^{lh}$
, isomorphic to
![]() $V_{M_h}^h$
via the map induced by
$V_{M_h}^h$
via the map induced by
![]() $\psi _h^{-1}\circ \psi$
.
$\psi _h^{-1}\circ \psi$
.
Recall the definition of
![]() $\phi$
in (1), which induces the glueing map between
$\phi$
in (1), which induces the glueing map between
![]() $V_{M_l}^l$
and
$V_{M_l}^l$
and
![]() $V_{M_h}^h$
. Since the following diagram
$V_{M_h}^h$
. Since the following diagram

is commutative, then the surjectivity of
follows from the separatedness of
![]() $X_\Delta ^{lh}$
.
$X_\Delta ^{lh}$
.
5.9. Properness
By [Reference Grothendieck and Dieudonné2, IV.15.7.10], it remains to show that
![]() $\mathcal{C}_s$
is proper. From [Reference Liu9, Exercise 3.3.11], we only need to prove that the
$\mathcal{C}_s$
is proper. From [Reference Liu9, Exercise 3.3.11], we only need to prove that the
![]() $1$
-dimensional subscheme
$1$
-dimensional subscheme
![]() $\Gamma _{\mathfrak{t}}$
is proper for every
$\Gamma _{\mathfrak{t}}$
is proper for every
![]() $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Indeed every other component is entirely contained in a model
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Indeed every other component is entirely contained in a model
![]() $\mathcal{C}_\Delta ^{w_h}$
, which is proper (see Section 5.5). Let
$\mathcal{C}_\Delta ^{w_h}$
, which is proper (see Section 5.5). Let
![]() $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
for some
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
for some
![]() $h,l=1,\dots,m$
, with
$h,l=1,\dots,m$
, with
![]() $h\neq l$
. For any
$h\neq l$
. For any
![]() $o=1,\dots, m$
such that
$o=1,\dots, m$
such that
![]() ${\mathfrak{s}}_o\subset \mathfrak{t}$
, let
${\mathfrak{s}}_o\subset \mathfrak{t}$
, let
![]() $\mathfrak{t}_o$
be the unique child of
$\mathfrak{t}_o$
be the unique child of
![]() $\mathfrak{t}$
with
$\mathfrak{t}$
with
![]() ${\mathfrak{s}}_o\subseteq \mathfrak{t}_o\lt \mathfrak{t}$
. Then
${\mathfrak{s}}_o\subseteq \mathfrak{t}_o\lt \mathfrak{t}$
. Then
![]() $\Gamma _{\mathfrak{t}}$
is equal to the glueing of the schemes
$\Gamma _{\mathfrak{t}}$
is equal to the glueing of the schemes
and
for all
![]() $o$
such that
$o$
such that
![]() ${\mathfrak{s}}_o\subset \mathfrak{t}$
, through the isomorphism (4) and the glueing maps in the definition of
${\mathfrak{s}}_o\subset \mathfrak{t}$
, through the isomorphism (4) and the glueing maps in the definition of
![]() $\mathcal{C}_\Delta ^{w_o}$
. In particular, for any
$\mathcal{C}_\Delta ^{w_o}$
. In particular, for any
![]() $o$
as above there exists a natural birational map
$o$
as above there exists a natural birational map
![]() $s_o\;:\;\Gamma _{\mathfrak{t}}\dashrightarrow \bar{X}_{F_{\mathfrak{t}}^{w_o}}$
which is defined as the identity morphism on the dense open
$s_o\;:\;\Gamma _{\mathfrak{t}}\dashrightarrow \bar{X}_{F_{\mathfrak{t}}^{w_o}}$
which is defined as the identity morphism on the dense open
![]() $ X_{F_{\mathfrak{t}}^{w_o}}=\Gamma _{\mathfrak{t}}\cap\mathring{\mathcal{C}}_\Delta ^{w_o}$
.
$ X_{F_{\mathfrak{t}}^{w_o}}=\Gamma _{\mathfrak{t}}\cap\mathring{\mathcal{C}}_\Delta ^{w_o}$
.
Let
![]() $D/k$
be a normal curve, let
$D/k$
be a normal curve, let
![]() $P\in D$
and let
$P\in D$
and let
![]() $D\smallsetminus \{P\}\stackrel{g}{\longrightarrow } \Gamma _{\mathfrak{t}}$
be a non-constant morphism of curves. We want to show that
$D\smallsetminus \{P\}\stackrel{g}{\longrightarrow } \Gamma _{\mathfrak{t}}$
be a non-constant morphism of curves. We want to show that
![]() $g$
extends to
$g$
extends to
![]() $D$
. For every
$D$
. For every
![]() $o$
as above,
$o$
as above,
![]() $\bar{X}_{F_{\mathfrak{t}}^{w_o}}$
is proper, so the birational map
$\bar{X}_{F_{\mathfrak{t}}^{w_o}}$
is proper, so the birational map
extends to a morphism
![]() $\bar{g}_o\; : \;D\longrightarrow \bar{X}_{F_{\mathfrak{t}}^{w_o}}$
. If
$\bar{g}_o\; : \;D\longrightarrow \bar{X}_{F_{\mathfrak{t}}^{w_o}}$
. If
for some
![]() $o$
such that
$o$
such that
![]() ${\mathfrak{s}}_o\subset \mathfrak{t}$
(we will later show this is always the case), then there exists an open neighbourhood
${\mathfrak{s}}_o\subset \mathfrak{t}$
(we will later show this is always the case), then there exists an open neighbourhood
![]() $U$
of
$U$
of
![]() $P_o$
such that
$P_o$
such that
![]() $U\subseteq \left (\bar{X}_{F_{\mathfrak{t}}^{w_o}}\cap\mathring{\mathcal{C}}_\Delta ^{w_o}\right )$
and so
$U\subseteq \left (\bar{X}_{F_{\mathfrak{t}}^{w_o}}\cap\mathring{\mathcal{C}}_\Delta ^{w_o}\right )$
and so
![]() $s_o|_{s_o^{-1}(U)}^U$
is an isomorphism. Since
$s_o|_{s_o^{-1}(U)}^U$
is an isomorphism. Since
![]() $P\in \bar{g}_o^{-1}(U)$
, the map
$P\in \bar{g}_o^{-1}(U)$
, the map
induces an extension
![]() $D\longrightarrow \Gamma _{\mathfrak{t}}$
of
$D\longrightarrow \Gamma _{\mathfrak{t}}$
of
![]() $g$
.
$g$
.
Suppose that
![]() $P_o\notin \bar{X}_{F_{\mathfrak{t}}^{w_o}}\cap\mathring{\mathcal{C}}_\Delta ^{w_o}$
for any
$P_o\notin \bar{X}_{F_{\mathfrak{t}}^{w_o}}\cap\mathring{\mathcal{C}}_\Delta ^{w_o}$
for any
![]() $o$
such that
$o$
such that
![]() ${\mathfrak{s}}_o\subset \mathfrak{t}$
. From Section 5.5 we have
${\mathfrak{s}}_o\subset \mathfrak{t}$
. From Section 5.5 we have
where
![]() $M=M_{L_{\mathfrak{t}}^{w_o},0}$
, and the product runs over all
$M=M_{L_{\mathfrak{t}}^{w_o},0}$
, and the product runs over all
![]() $l\neq o$
such that
$l\neq o$
such that
![]() $\mathfrak{t}={\mathfrak{s}}_o\wedge{\mathfrak{s}}_l$
. In particular
$\mathfrak{t}={\mathfrak{s}}_o\wedge{\mathfrak{s}}_l$
. In particular
![]() $P_o$
is a point of each irreducible component of
$P_o$
is a point of each irreducible component of
![]() $\bar{X}_{F_{\mathfrak{t}}^{w_o}}$
by Lemma 5.17. Let
$\bar{X}_{F_{\mathfrak{t}}^{w_o}}$
by Lemma 5.17. Let
![]() $h\neq o$
such that
$h\neq o$
such that
![]() $X+u_{oh}$
vanishes at
$X+u_{oh}$
vanishes at
![]() $P_o$
. Let
$P_o$
. Let
![]() $\xi$
be the generic point of
$\xi$
be the generic point of
![]() $D$
and let
$D$
and let
![]() $\xi _o=g_o(\xi )$
,
$\xi _o=g_o(\xi )$
,
![]() $\xi _h=g_h(\xi )$
be generic points of
$\xi _h=g_h(\xi )$
be generic points of
![]() $\bar{X}_{F_{\mathfrak{t}}^{w_o}}$
and
$\bar{X}_{F_{\mathfrak{t}}^{w_o}}$
and
![]() $\bar{X}_{F_{\mathfrak{t}}^{w_h}}$
respectively. Then the birational maps
$\bar{X}_{F_{\mathfrak{t}}^{w_h}}$
respectively. Then the birational maps
![]() $s_o$
and
$s_o$
and
![]() $s_h$
give
$s_h$
give

where we denote by
![]() $\phi _{g_o}$
and
$\phi _{g_o}$
and
![]() $\phi _{g_h}$
the homomorphisms between function fields induced by
$\phi _{g_h}$
the homomorphisms between function fields induced by
![]() $g_o$
and
$g_o$
and
![]() $g_h$
. The vertical isomorphism is induced by the map
$g_h$
. The vertical isomorphism is induced by the map
which sends (see Section 5.3 and Lemma 5.7)
But the rational function
![]() $X+u_{oh}$
vanishes at
$X+u_{oh}$
vanishes at
![]() $P_o$
, while
$P_o$
, while
![]() $X$
does not vanish at
$X$
does not vanish at
![]() $P_h$
by (9). This gives a contradiction, as
$P_h$
by (9). This gives a contradiction, as
![]() $\bar{g}_o(P)=P_o$
and
$\bar{g}_o(P)=P_o$
and
![]() $\bar{g}_h(P)=P_h$
.
$\bar{g}_h(P)=P_h$
.
5.10. Genus
Suppose
![]() $\Sigma =\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}=\Sigma _C^{\textrm{min}}$
, and
$\Sigma =\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}=\Sigma _C^{\textrm{min}}$
, and
![]() $C$
has an almost rational cluster picture and is
$C$
has an almost rational cluster picture and is
![]() $y$
-regular. In the previous subsections we proved that
$y$
-regular. In the previous subsections we proved that
![]() $\mathcal{C}/O_K$
is a proper regular model of
$\mathcal{C}/O_K$
is a proper regular model of
![]() $C$
. Let
$C$
. Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster.
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster.
Proposition 5.21.
Let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
. Then
$\mathfrak{t}\in \Sigma _C^{w_h}$
. Then
![]() $\Gamma _{\mathfrak{t}}$
is isomorphic to the smooth projective
$\Gamma _{\mathfrak{t}}$
is isomorphic to the smooth projective
![]() $1$
-dimensional scheme given by
$1$
-dimensional scheme given by
where
![]() ${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
${\overline{u_{w_{\mathfrak{s}} w_h}}}=\frac{w_{\mathfrak{s}}-w_h}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
, and
![]() $w_{\mathfrak{s}}$
is any rational centre of
$w_{\mathfrak{s}}$
is any rational centre of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
In particular,
-
(1) if
 $D_{\mathfrak{t}}=1$
, then
$D_{\mathfrak{t}}=1$
, then
 $\Gamma _{\mathfrak{t}}\simeq{\mathbb{P}}^1_k$
;
$\Gamma _{\mathfrak{t}}\simeq{\mathbb{P}}^1_k$
; -
(2) if
 $D_{\mathfrak{t}}=2$
and
$D_{\mathfrak{t}}=2$
and
 $\mathfrak{t}$
is übereven, then
$\mathfrak{t}$
is übereven, then
 $\Gamma _{\mathfrak{t}}$
is the disjoint union of two
$\Gamma _{\mathfrak{t}}$
is the disjoint union of two
 ${\mathbb{P}}^1$
s over some quadratic extension of
${\mathbb{P}}^1$
s over some quadratic extension of
 $k$
;
$k$
; -
(3) in all other cases,
 $\Gamma _{\mathfrak{t}}$
is a hyperelliptic curve of genus
$\Gamma _{\mathfrak{t}}$
is a hyperelliptic curve of genus
 $g(\mathfrak{t})$
.
$g(\mathfrak{t})$
.
Proof. The first part of the proposition follows from Proposition 5.18.
For the second part of the statement note that if
![]() $D_{\mathfrak{t}}=1$
then the result follows. Suppose
$D_{\mathfrak{t}}=1$
then the result follows. Suppose
![]() $D_{\mathfrak{t}}=2$
. Then
$D_{\mathfrak{t}}=2$
. Then
![]() $p\neq 2$
as
$p\neq 2$
as
![]() $C$
is
$C$
is
![]() $y$
-regular. Note that since
$y$
-regular. Note that since
![]() $\Sigma =\Sigma _C^{\textrm{min}}$
, the proper clusters in
$\Sigma =\Sigma _C^{\textrm{min}}$
, the proper clusters in
![]() $\Sigma ^W$
correspond to the proper clusters in
$\Sigma ^W$
correspond to the proper clusters in
![]() $\Sigma _C^{\textrm{rat}}$
. Recall the definition of
$\Sigma _C^{\textrm{rat}}$
. Recall the definition of
![]() $\tilde{\mathfrak{t}}$
given in Definition 4.13. Let
$\tilde{\mathfrak{t}}$
given in Definition 4.13. Let
![]() $h(X)=\prod _{\mathfrak{s}\in \tilde{\mathfrak{t}}^W}(X-{\overline{u_{w_{\mathfrak{s}} w_h}}}){\overline{f_{\mathfrak{t},w_h}}}(X)$
.
$h(X)=\prod _{\mathfrak{s}\in \tilde{\mathfrak{t}}^W}(X-{\overline{u_{w_{\mathfrak{s}} w_h}}}){\overline{f_{\mathfrak{t},w_h}}}(X)$
.
Suppose
![]() $\mathfrak{t}$
is übereven. Then all its children are (proper) rational cluster by Lemma 3.30 since they are even and
$\mathfrak{t}$
is übereven. Then all its children are (proper) rational cluster by Lemma 3.30 since they are even and
![]() $p\neq 2$
. In particular
$p\neq 2$
. In particular
![]() $b_{\mathfrak{t}}=1$
by Lemma 3.18 and so
$b_{\mathfrak{t}}=1$
by Lemma 3.18 and so
![]() $\epsilon _{\mathfrak{t}}\in 2\mathbb{Z}$
and
$\epsilon _{\mathfrak{t}}\in 2\mathbb{Z}$
and
![]() $\tilde{\mathfrak{t}}=\tilde{\mathfrak{t}}^W=\varnothing$
since it equals the set of odd rational children. Moreover,
$\tilde{\mathfrak{t}}=\tilde{\mathfrak{t}}^W=\varnothing$
since it equals the set of odd rational children. Moreover,
![]() $\mathfrak{t}=\bigcup _{\mathfrak{s}\lt \mathfrak{t},\,\mathfrak{s}\,\text{proper}}\mathfrak{s}$
, and so
$\mathfrak{t}=\bigcup _{\mathfrak{s}\lt \mathfrak{t},\,\mathfrak{s}\,\text{proper}}\mathfrak{s}$
, and so
![]() ${\overline{f_{\mathfrak{t},w_h}}}\in k$
. Thus
${\overline{f_{\mathfrak{t},w_h}}}\in k$
. Thus
![]() $h(X)\in k$
.
$h(X)\in k$
.
Now suppose
![]() $h(X)\in k$
. Then
$h(X)\in k$
. Then
![]() $\tilde{\mathfrak{t}}^W=\varnothing$
and
$\tilde{\mathfrak{t}}^W=\varnothing$
and
![]() $\mathfrak{t}=\bigcup _{\mathfrak{s}\lt \mathfrak{t}}\mathfrak{s}$
, where
$\mathfrak{t}=\bigcup _{\mathfrak{s}\lt \mathfrak{t}}\mathfrak{s}$
, where
![]() $\mathfrak{s}$
runs through all children
$\mathfrak{s}$
runs through all children
![]() $\mathfrak{s}\in \Sigma ^W$
of
$\mathfrak{s}\in \Sigma ^W$
of
![]() $\mathfrak{t}$
. The non-proper clusters in
$\mathfrak{t}$
. The non-proper clusters in
![]() $\Sigma ^W$
are of the form
$\Sigma ^W$
are of the form
![]() $\{w_l\}$
for some
$\{w_l\}$
for some
![]() $l=1,\dots,m$
. If
$l=1,\dots,m$
. If
![]() $\{w_l\}\lt \mathfrak{t}$
, then
$\{w_l\}\lt \mathfrak{t}$
, then
![]() $\mathfrak{t}={\mathfrak{s}}_l$
, but in that case
$\mathfrak{t}={\mathfrak{s}}_l$
, but in that case
![]() $\mathfrak{t}$
would not equal the union of its children in
$\mathfrak{t}$
would not equal the union of its children in
![]() $\Sigma ^W$
. Hence
$\Sigma ^W$
. Hence
![]() $\mathfrak{t}$
has no non-proper children. It follows that
$\mathfrak{t}$
has no non-proper children. It follows that
![]() $\tilde{\mathfrak{t}}=\tilde{\mathfrak{t}}^W$
and
$\tilde{\mathfrak{t}}=\tilde{\mathfrak{t}}^W$
and
![]() $\mathfrak{t}$
equals the union of its proper rational children. In particular,
$\mathfrak{t}$
equals the union of its proper rational children. In particular,
![]() $\mathfrak{t}$
has two or more children in
$\mathfrak{t}$
has two or more children in
![]() $\Sigma _C^{\textrm{rat}}$
, so
$\Sigma _C^{\textrm{rat}}$
, so
![]() $b_{\mathfrak{t}}=1$
, by Lemma 3.18. But then
$b_{\mathfrak{t}}=1$
, by Lemma 3.18. But then
![]() $\tilde{\mathfrak{t}}$
is the set of odd children of
$\tilde{\mathfrak{t}}$
is the set of odd children of
![]() $\mathfrak{t}$
as
$\mathfrak{t}$
as
![]() $\epsilon _{\mathfrak{t}}\in 2\mathbb{Z}$
, and so all rational children of
$\epsilon _{\mathfrak{t}}\in 2\mathbb{Z}$
, and so all rational children of
![]() $\mathfrak{t}$
are even.
$\mathfrak{t}$
are even.
It only remains to prove that if
![]() $h(x)\notin k$
, then the genus of
$h(x)\notin k$
, then the genus of
![]() $\Gamma _{\mathfrak{t}}$
is
$\Gamma _{\mathfrak{t}}$
is
![]() $g(\mathfrak{t})$
. Since
$g(\mathfrak{t})$
. Since
![]() $h(X)$
is a separable polynomial, we need to show that
$h(X)$
is a separable polynomial, we need to show that
It suffices to prove that if
![]() $\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
is a non-proper rational child of
$\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
is a non-proper rational child of
![]() $\mathfrak{t}$
different from
$\mathfrak{t}$
different from
![]() $\{w_h\}$
, then
$\{w_h\}$
, then
![]() $b_{\mathfrak{t}}=1$
and
$b_{\mathfrak{t}}=1$
and
![]() $\mathfrak{s}\in \tilde{\mathfrak{t}}$
. Suppose
$\mathfrak{s}\in \tilde{\mathfrak{t}}$
. Suppose
![]() $\mathfrak{s}=\{r\}$
is such a rational cluster. Since
$\mathfrak{s}=\{r\}$
is such a rational cluster. Since
![]() $r\in \mathfrak{t}$
, we have
$r\in \mathfrak{t}$
, we have
![]() $v(r-w_h)\geq \rho _{\mathfrak{t}}$
. Suppose
$v(r-w_h)\geq \rho _{\mathfrak{t}}$
. Suppose
![]() $v(r-w_h)\gt \rho _{\mathfrak{t}}$
. Then
$v(r-w_h)\gt \rho _{\mathfrak{t}}$
. Then
![]() $\mathfrak{s}\in \Sigma _C^{w_h}$
, as
$\mathfrak{s}\in \Sigma _C^{w_h}$
, as
![]() $\mathfrak{s}\lt \mathfrak{t}$
and
$\mathfrak{s}\lt \mathfrak{t}$
and
![]() $r\neq w_h$
. But this contradicts our choice of
$r\neq w_h$
. But this contradicts our choice of
![]() $W$
. Then
$W$
. Then
![]() $\rho _{\mathfrak{t}}=v(r-w_h)\in \mathbb{Z}$
and so
$\rho _{\mathfrak{t}}=v(r-w_h)\in \mathbb{Z}$
and so
![]() $b_{\mathfrak{t}}=1$
. It follows that
$b_{\mathfrak{t}}=1$
. It follows that
![]() $\tilde{\mathfrak{t}}$
is the set of odd children of
$\tilde{\mathfrak{t}}$
is the set of odd children of
![]() $\mathfrak{t}$
. Thus
$\mathfrak{t}$
. Thus
![]() $\mathfrak{s}\in \tilde{\mathfrak{t}}$
.
$\mathfrak{s}\in \tilde{\mathfrak{t}}$
.
5.11. Minimal regular NC model
Suppose the base extended curve
![]() $C_{K^{nr}}$
is
$C_{K^{nr}}$
is
![]() $y$
-regular and has an almost rational cluster picture. Consider the model
$y$
-regular and has an almost rational cluster picture. Consider the model
![]() $\mathcal{C}/O_{K^{nr}}$
constructed before with
$\mathcal{C}/O_{K^{nr}}$
constructed before with
![]() $\Sigma =\Sigma _{C_{K^{nr}}}^{\textrm{min}}$
. We want to see what components of
$\Sigma =\Sigma _{C_{K^{nr}}}^{\textrm{min}}$
. We want to see what components of
![]() $\mathcal{C}_s$
should be blown down to obtain the minimal regular model with normal crossings. Recall [Reference Dokchitser1, §5]. Let
$\mathcal{C}_s$
should be blown down to obtain the minimal regular model with normal crossings. Recall [Reference Dokchitser1, §5]. Let
![]() $\Sigma _{K^{nr}}=\Sigma _{C_{K^{nr}}}^{\textrm{rat}}$
and fix a proper cluster
$\Sigma _{K^{nr}}=\Sigma _{C_{K^{nr}}}^{\textrm{rat}}$
and fix a proper cluster
![]() $\mathfrak{t}\in \Sigma _{C_{K^{nr}}}^{w_h}$
.
$\mathfrak{t}\in \Sigma _{C_{K^{nr}}}^{w_h}$
.
Suppose first
![]() $\mathfrak{t}\neq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
for all
$\mathfrak{t}\neq{\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
for all
![]() $l=1,\dots,m$
with
$l=1,\dots,m$
with
![]() $l\neq h$
. Equivalently,
$l\neq h$
. Equivalently,
![]() $\mathfrak{t}$
has at most one proper child in
$\mathfrak{t}$
has at most one proper child in
![]() $\Sigma _{K^{nr}}$
. Then
$\Sigma _{K^{nr}}$
. Then
![]() $\Gamma _{\mathfrak{t}}\simeq \bar{X}_{F_{\mathfrak{t}}^{w_h}}$
and can be seen entirely in
$\Gamma _{\mathfrak{t}}\simeq \bar{X}_{F_{\mathfrak{t}}^{w_h}}$
and can be seen entirely in
![]() $\mathring{\mathcal{C}}_{\Delta }^{w_h}$
. In particular, if
$\mathring{\mathcal{C}}_{\Delta }^{w_h}$
. In particular, if
![]() $\Gamma _{\mathfrak{t}}$
can be blown down then
$\Gamma _{\mathfrak{t}}$
can be blown down then
![]() $F_{\mathfrak{t}}^{w_h}$
is a removable or contractible
$F_{\mathfrak{t}}^{w_h}$
is a removable or contractible
![]() $v$
-face (see [Reference Dokchitser1, Theorem 5.7]). By Lemma 4.3, we find
$v$
-face (see [Reference Dokchitser1, Theorem 5.7]). By Lemma 4.3, we find
-
 $F_{\mathfrak{t}}^{w_h}$
is removable if and only if
$F_{\mathfrak{t}}^{w_h}$
is removable if and only if
 $\mathfrak{t}=\mathfrak{R}$
with a child in
$\mathfrak{t}=\mathfrak{R}$
with a child in
 $\Sigma _{K^{nr}}$
of size
$\Sigma _{K^{nr}}$
of size
 $2g+1$
.
$2g+1$
. -
 $F_{\mathfrak{t}}^{w_h}$
is contractible if and only if either
$F_{\mathfrak{t}}^{w_h}$
is contractible if and only if either
 $|\mathfrak{t}|=2$
and
$|\mathfrak{t}|=2$
and
 $\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}\in \mathbb{Z}$
or
$\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}\in \mathbb{Z}$
or
 $\mathfrak{t}$
has a proper rational child
$\mathfrak{t}$
has a proper rational child
 $\mathfrak{s}\in \Sigma _{K^{nr}}$
, of size
$\mathfrak{s}\in \Sigma _{K^{nr}}$
, of size
 $2g$
, and
$2g$
, and
 $\frac{\epsilon _{\mathfrak{t}}}{2}-g\rho _{\mathfrak{t}}\in \mathbb{Z}$
.
$\frac{\epsilon _{\mathfrak{t}}}{2}-g\rho _{\mathfrak{t}}\in \mathbb{Z}$
.
Recall Definition 4.20. Note that
![]() $F_{\mathfrak{t}}^{w_h}$
is removable if and only if
$F_{\mathfrak{t}}^{w_h}$
is removable if and only if
![]() $\mathfrak{t}$
is removable. In this case,
$\mathfrak{t}$
is removable. In this case,
![]() $F_{\mathfrak{t}}^{w_h}$
can be ignored for the construction of
$F_{\mathfrak{t}}^{w_h}$
can be ignored for the construction of
![]() $\mathcal{C}_\Delta ^{w_h}$
(for any
$\mathcal{C}_\Delta ^{w_h}$
(for any
![]() $h$
since
$h$
since
![]() $\mathfrak{t}=\mathfrak{R}$
), and so
$\mathfrak{t}=\mathfrak{R}$
), and so
![]() $\mathfrak{t}$
can be ignored for the construction of
$\mathfrak{t}$
can be ignored for the construction of
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
Assume now
![]() $F_{\mathfrak{t}}^{w_h}$
contractible. We want to understand when
$F_{\mathfrak{t}}^{w_h}$
contractible. We want to understand when
![]() $\Gamma _{\mathfrak{t}}$
can be blown down. First consider the case
$\Gamma _{\mathfrak{t}}$
can be blown down. First consider the case
![]() $|\mathfrak{t}|=2$
and
$|\mathfrak{t}|=2$
and
![]() $\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}\in \mathbb{Z}$
. Then
$\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}\in \mathbb{Z}$
. Then
![]() $\Gamma _{\mathfrak{t}}$
intersects other components of
$\Gamma _{\mathfrak{t}}$
intersects other components of
![]() $\mathcal{C}_s$
in
$\mathcal{C}_s$
in
![]() $2$
points (as
$2$
points (as
![]() $V_{\mathfrak{t}}^{w_h}$
gives two chains of
$V_{\mathfrak{t}}^{w_h}$
gives two chains of
![]() ${\mathbb{P}}^1$
s and the
${\mathbb{P}}^1$
s and the
![]() $v$
-edges
$v$
-edges
![]() $V_0^{w_h}$
and
$V_0^{w_h}$
and
![]() $L_{\mathfrak{t}}^{w_h}$
give no component in
$L_{\mathfrak{t}}^{w_h}$
give no component in
![]() $\mathcal{C}_{\Delta,s}^{w_h}$
). To have self-intersection
$\mathcal{C}_{\Delta,s}^{w_h}$
). To have self-intersection
![]() $-1$
,
$-1$
,
![]() $\Gamma _{\mathfrak{t}}$
has to have multiplicity
$\Gamma _{\mathfrak{t}}$
has to have multiplicity
![]() $\gt 1$
. It follows from Lemma 5.16 that
$\gt 1$
. It follows from Lemma 5.16 that
![]() $\rho _{\mathfrak{t}}\notin \mathbb{Z}$
, as
$\rho _{\mathfrak{t}}\notin \mathbb{Z}$
, as
![]() $\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}\in \mathbb{Z}$
. Moreover, by Lemma 3.12, one has
$\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}\in \mathbb{Z}$
. Moreover, by Lemma 3.12, one has
![]() $\rho _{\mathfrak{t}}\in \frac{1}{2}\mathbb{Z}$
. Therefore
$\rho _{\mathfrak{t}}\in \frac{1}{2}\mathbb{Z}$
. Therefore
![]() $\epsilon _{\mathfrak{t}}$
is odd and the multiplicity of
$\epsilon _{\mathfrak{t}}$
is odd and the multiplicity of
![]() $\Gamma _{\mathfrak{t}}$
is
$\Gamma _{\mathfrak{t}}$
is
![]() $2$
. Let
$2$
. Let
![]() $r\;:\!=\;r_{V_{\mathfrak{t}}^{w_h}}$
and consider
$r\;:\!=\;r_{V_{\mathfrak{t}}^{w_h}}$
and consider
given by
![]() $V_{\mathfrak{t}}^{w_h}$
. If
$V_{\mathfrak{t}}^{w_h}$
. If
![]() $\Gamma _{\mathfrak{t}}$
can be blown down then
$\Gamma _{\mathfrak{t}}$
can be blown down then
![]() $d_1=1$
. Since
$d_1=1$
. Since
![]() $\gamma _{\mathfrak{t}} s_{\mathfrak{t}}=-\frac{\epsilon _{\mathfrak{t}}}{2}+2\rho _{\mathfrak{t}}$
, we have
$\gamma _{\mathfrak{t}} s_{\mathfrak{t}}=-\frac{\epsilon _{\mathfrak{t}}}{2}+2\rho _{\mathfrak{t}}$
, we have
![]() $d_0=2$
. In particular
$d_0=2$
. In particular
![]() $d_1=1$
if and only if
$d_1=1$
if and only if
![]() $\rho _{\mathfrak{t}}-\rho _{P(\mathfrak{t})}=\frac{n_0}{d_0}-\frac{n_{r+1}}{d_{r+1}}\geq \frac{1}{2}$
(see also [Reference Dokchitser1, Remark 3.15]). Thus if
$\rho _{\mathfrak{t}}-\rho _{P(\mathfrak{t})}=\frac{n_0}{d_0}-\frac{n_{r+1}}{d_{r+1}}\geq \frac{1}{2}$
(see also [Reference Dokchitser1, Remark 3.15]). Thus if
![]() $|\mathfrak{t}|=2$
, then
$|\mathfrak{t}|=2$
, then
![]() $\Gamma _{\mathfrak{t}}$
can be blown down if and only if
$\Gamma _{\mathfrak{t}}$
can be blown down if and only if
![]() $\rho _{\mathfrak{t}}\notin \mathbb{Z}$
,
$\rho _{\mathfrak{t}}\notin \mathbb{Z}$
,
![]() $\epsilon _{\mathfrak{t}}$
odd,
$\epsilon _{\mathfrak{t}}$
odd,
![]() $\rho _{P(\mathfrak{t})}\leq \rho _{\mathfrak{t}}-\frac{1}{2}$
. Note that this is case (1) of Definition 4.20.
$\rho _{P(\mathfrak{t})}\leq \rho _{\mathfrak{t}}-\frac{1}{2}$
. Note that this is case (1) of Definition 4.20.
Second consider the case
![]() $|\mathfrak{t}|=2g+2$
with a proper rational child
$|\mathfrak{t}|=2g+2$
with a proper rational child
![]() $\mathfrak{s}$
of size
$\mathfrak{s}$
of size
![]() $2g$
and
$2g$
and
![]() $\tfrac{\epsilon _{\mathfrak{t}}}{2}-g\rho _{\mathfrak{t}}\in \mathbb{Z}$
. The argument is very similar to the previous one. If
$\tfrac{\epsilon _{\mathfrak{t}}}{2}-g\rho _{\mathfrak{t}}\in \mathbb{Z}$
. The argument is very similar to the previous one. If
![]() $\Gamma _{\mathfrak{t}}$
can be blown down then it must have multiplicity
$\Gamma _{\mathfrak{t}}$
can be blown down then it must have multiplicity
![]() $\gt 1$
and this implies
$\gt 1$
and this implies
![]() $\rho _{\mathfrak{t}}\notin \mathbb{Z}$
again by Lemma 5.16. From Lemma 3.12 it follows that
$\rho _{\mathfrak{t}}\notin \mathbb{Z}$
again by Lemma 5.16. From Lemma 3.12 it follows that
![]() $(|\mathfrak{t}|-|\mathfrak{s}|)\rho _{\mathfrak{t}}\in \mathbb{Z}$
, so
$(|\mathfrak{t}|-|\mathfrak{s}|)\rho _{\mathfrak{t}}\in \mathbb{Z}$
, so
![]() $\rho _{\mathfrak{t}}\in \frac{1}{2}\mathbb{Z}$
. Then
$\rho _{\mathfrak{t}}\in \frac{1}{2}\mathbb{Z}$
. Then
![]() $m_{\mathfrak{t}}=2$
and
$m_{\mathfrak{t}}=2$
and
so
![]() $v(c_f)$
odd. Let
$v(c_f)$
odd. Let
![]() $r\;:\!=\;r_{V_{\mathfrak{s}}^{w_h}}$
and consider
$r\;:\!=\;r_{V_{\mathfrak{s}}^{w_h}}$
and consider
given by
![]() $V_{\mathfrak{s}}^{w_h}$
. If
$V_{\mathfrak{s}}^{w_h}$
. If
![]() $\Gamma _{\mathfrak{t}}$
can be blown down then
$\Gamma _{\mathfrak{t}}$
can be blown down then
![]() $d_r=1$
. Recall that
$d_r=1$
. Recall that
![]() $\epsilon _{\mathfrak{s}}-|\mathfrak{s}|\rho _{\mathfrak{s}}=\epsilon _{\mathfrak{t}}-|\mathfrak{s}|\rho _{\mathfrak{t}}$
. Then
$\epsilon _{\mathfrak{s}}-|\mathfrak{s}|\rho _{\mathfrak{s}}=\epsilon _{\mathfrak{t}}-|\mathfrak{s}|\rho _{\mathfrak{t}}$
. Then
![]() $\gamma _{\mathfrak{s}}(s_{\mathfrak{s}}-\rho _{\mathfrak{s}}+\rho _{\mathfrak{t}})=-\frac{\epsilon _{\mathfrak{t}}}{2}+(g+1)\rho _{\mathfrak{t}}$
, so
$\gamma _{\mathfrak{s}}(s_{\mathfrak{s}}-\rho _{\mathfrak{s}}+\rho _{\mathfrak{t}})=-\frac{\epsilon _{\mathfrak{t}}}{2}+(g+1)\rho _{\mathfrak{t}}$
, so
![]() $d_{r+1}=2$
. In particular
$d_{r+1}=2$
. In particular
![]() $d_r=1$
if and only if
$d_r=1$
if and only if
![]() $\rho _{\mathfrak{s}}-\rho _{\mathfrak{t}}=\frac{n_0}{d_0}-\frac{n_{r+1}}{d_{r+1}}\geq \frac{1}{2}$
. Thus if
$\rho _{\mathfrak{s}}-\rho _{\mathfrak{t}}=\frac{n_0}{d_0}-\frac{n_{r+1}}{d_{r+1}}\geq \frac{1}{2}$
. Thus if
![]() $\mathfrak{t}$
has size
$\mathfrak{t}$
has size
![]() $2g+2$
and has a unique proper rational child
$2g+2$
and has a unique proper rational child
![]() $\mathfrak{s}\in \Sigma _{K^{nr}}$
, then
$\mathfrak{s}\in \Sigma _{K^{nr}}$
, then
![]() $\Gamma _{\mathfrak{t}}$
can be blown down if and only if
$\Gamma _{\mathfrak{t}}$
can be blown down if and only if
![]() $|\mathfrak{s}|=2g$
,
$|\mathfrak{s}|=2g$
,
![]() $\rho _{\mathfrak{t}}\notin \mathbb{Z}$
,
$\rho _{\mathfrak{t}}\notin \mathbb{Z}$
,
![]() $v(c_f)$
odd,
$v(c_f)$
odd,
![]() $\rho _{\mathfrak{s}}\geq \rho _{\mathfrak{t}}+\frac{1}{2}$
. This is case (2) of Definition 4.20.
$\rho _{\mathfrak{s}}\geq \rho _{\mathfrak{t}}+\frac{1}{2}$
. This is case (2) of Definition 4.20.
Finally, if
![]() $|\mathfrak{t}|=2g+1$
,
$|\mathfrak{t}|=2g+1$
,
![]() $\mathfrak{t}$
has a proper child
$\mathfrak{t}$
has a proper child
![]() $\mathfrak{s}\in \Sigma _{K^{nr}}$
of size
$\mathfrak{s}\in \Sigma _{K^{nr}}$
of size
![]() $2g$
and
$2g$
and
![]() $\frac{\epsilon _{\mathfrak{t}}}{2}-g\rho _{\mathfrak{t}}\in \mathbb{Z}$
, then
$\frac{\epsilon _{\mathfrak{t}}}{2}-g\rho _{\mathfrak{t}}\in \mathbb{Z}$
, then
![]() $\rho _{\mathfrak{t}}\in \mathbb{Z}$
, as
$\rho _{\mathfrak{t}}\in \mathbb{Z}$
, as
![]() $(|\mathfrak{t}|-|\mathfrak{s}|)\rho _{\mathfrak{t}}\in \mathbb{Z}$
. It follows that
$(|\mathfrak{t}|-|\mathfrak{s}|)\rho _{\mathfrak{t}}\in \mathbb{Z}$
. It follows that
![]() $\epsilon _{\mathfrak{t}}\in \mathbb{Z}$
and so
$\epsilon _{\mathfrak{t}}\in \mathbb{Z}$
and so
![]() $m_{\mathfrak{t}}=1$
. This implies the self-intersection of
$m_{\mathfrak{t}}=1$
. This implies the self-intersection of
![]() $\Gamma _{\mathfrak{t}}$
is not
$\Gamma _{\mathfrak{t}}$
is not
![]() $-1$
, since it intersects the rest of
$-1$
, since it intersects the rest of
![]() $\mathcal{C}_{\mathfrak{t}}$
in at least two points as before. Hence in this case
$\mathcal{C}_{\mathfrak{t}}$
in at least two points as before. Hence in this case
![]() $\Gamma _{\mathfrak{t}}$
can never be blown down.
$\Gamma _{\mathfrak{t}}$
can never be blown down.
Now assume there exists
![]() $l\neq h$
such that
$l\neq h$
such that
![]() $\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Then
$\mathfrak{t}={\mathfrak{s}}_h\wedge{\mathfrak{s}}_l$
. Then
![]() $\mathfrak{t}$
is not minimal. Let
$\mathfrak{t}$
is not minimal. Let
![]() $\mathfrak{t}_h,\mathfrak{t}_l\in \Sigma _{K^{nr}}$
be such that
$\mathfrak{t}_h,\mathfrak{t}_l\in \Sigma _{K^{nr}}$
be such that
![]() ${\mathfrak{s}}_h\subseteq \mathfrak{t}_h\lt \mathfrak{t}$
and
${\mathfrak{s}}_h\subseteq \mathfrak{t}_h\lt \mathfrak{t}$
and
![]() ${\mathfrak{s}}_l\subseteq \mathfrak{t}_l\lt \mathfrak{t}$
. Suppose
${\mathfrak{s}}_l\subseteq \mathfrak{t}_l\lt \mathfrak{t}$
. Suppose
![]() $\Gamma _{\mathfrak{t}}$
irreducible. If
$\Gamma _{\mathfrak{t}}$
irreducible. If
![]() $|\mathfrak{t}|\leq 2g$
(or, equivalently,
$|\mathfrak{t}|\leq 2g$
(or, equivalently,
![]() $\mathfrak{t}$
is not the largest non-removable cluster), then
$\mathfrak{t}$
is not the largest non-removable cluster), then
![]() $\Gamma _{\mathfrak{t}}$
intersects at least other
$\Gamma _{\mathfrak{t}}$
intersects at least other
![]() $3$
components of
$3$
components of
![]() $\mathcal{C}_s$
(given by
$\mathcal{C}_s$
(given by
![]() $\mathfrak{t}_h,\mathfrak{t}_l$
, and
$\mathfrak{t}_h,\mathfrak{t}_l$
, and
![]() $P(\mathfrak{t})$
). So it cannot be contracted to obtain a model with normal crossings. A similar argument holds if there exists
$P(\mathfrak{t})$
). So it cannot be contracted to obtain a model with normal crossings. A similar argument holds if there exists
![]() $o\neq l$
such that
$o\neq l$
such that
![]() ${\mathfrak{s}}_o\wedge{\mathfrak{s}}_h=\mathfrak{t}$
: at least
${\mathfrak{s}}_o\wedge{\mathfrak{s}}_h=\mathfrak{t}$
: at least
![]() $3$
components (given by
$3$
components (given by
![]() $\mathfrak{t}_h$
,
$\mathfrak{t}_h$
,
![]() $\mathfrak{t}_l$
and
$\mathfrak{t}_l$
and
![]() $\mathfrak{t}_o$
) intersect
$\mathfrak{t}_o$
) intersect
![]() $\Gamma _{\mathfrak{t}}$
, so blowing down
$\Gamma _{\mathfrak{t}}$
, so blowing down
![]() $\Gamma _{\mathfrak{t}}$
would make the model lose normal crossings. Assume then
$\Gamma _{\mathfrak{t}}$
would make the model lose normal crossings. Assume then
![]() $|\mathfrak{t}|\gt 2g$
and
$|\mathfrak{t}|\gt 2g$
and
![]() ${\mathfrak{s}}_o\wedge{\mathfrak{s}}_h\neq \mathfrak{t}$
for all
${\mathfrak{s}}_o\wedge{\mathfrak{s}}_h\neq \mathfrak{t}$
for all
![]() $o\neq l$
. Then
$o\neq l$
. Then
![]() $\Gamma _{\mathfrak{t}}$
intersects at least other
$\Gamma _{\mathfrak{t}}$
intersects at least other
![]() $2$
components of
$2$
components of
![]() $\mathcal{C}_s$
given by
$\mathcal{C}_s$
given by
![]() $V_{\mathfrak{t}_h}^{w_h}$
and
$V_{\mathfrak{t}_h}^{w_h}$
and
![]() $V_{\mathfrak{t}_l}^{w_l}$
. Firstly, if
$V_{\mathfrak{t}_l}^{w_l}$
. Firstly, if
![]() $\Gamma _{\mathfrak{t}}$
can be blown down, then
$\Gamma _{\mathfrak{t}}$
can be blown down, then
![]() $m_{\mathfrak{t}}\gt 1$
. But
$m_{\mathfrak{t}}\gt 1$
. But
![]() $\rho _{\mathfrak{t}}=\rho _{hl}\in \mathbb{Z}$
. Then
$\rho _{\mathfrak{t}}=\rho _{hl}\in \mathbb{Z}$
. Then
![]() $m_{\mathfrak{t}}$
is at most
$m_{\mathfrak{t}}$
is at most
![]() $2$
. If
$2$
. If
![]() $m_{\mathfrak{t}}=2$
then
$m_{\mathfrak{t}}=2$
then
![]() $D_{\mathfrak{t}}=1$
, that implies
$D_{\mathfrak{t}}=1$
, that implies
![]() $\epsilon _{\mathfrak{t}}$
odd and
$\epsilon _{\mathfrak{t}}$
odd and
![]() $\Gamma _{\mathfrak{t}}\simeq{\mathbb{P}}^1$
by Proposition 5.21. It also follows
$\Gamma _{\mathfrak{t}}\simeq{\mathbb{P}}^1$
by Proposition 5.21. It also follows
![]() $s_{\mathfrak{t}}\in \tfrac{1}{2}\mathbb{Z}\setminus \mathbb{Z}$
. If
$s_{\mathfrak{t}}\in \tfrac{1}{2}\mathbb{Z}\setminus \mathbb{Z}$
. If
![]() $\mathfrak{t}$
is odd then this implies that
$\mathfrak{t}$
is odd then this implies that
![]() $V_{\mathfrak{t}}^{w_h}$
gives a
$V_{\mathfrak{t}}^{w_h}$
gives a
![]() ${\mathbb{P}}^1$
intersecting
${\mathbb{P}}^1$
intersecting
![]() $\Gamma _{\mathfrak{t}}$
. Since that would be a third component intersecting
$\Gamma _{\mathfrak{t}}$
. Since that would be a third component intersecting
![]() $\Gamma _{\mathfrak{t}}$
, the cluster
$\Gamma _{\mathfrak{t}}$
, the cluster
![]() $\mathfrak{t}$
has to be even. Hence
$\mathfrak{t}$
has to be even. Hence
![]() $\mathfrak{t}=\mathfrak{R}$
and
$\mathfrak{t}=\mathfrak{R}$
and
![]() $|\mathfrak{t}|=2g+2$
. Then
$|\mathfrak{t}|=2g+2$
. Then
![]() $\epsilon _{\mathfrak{t}}$
is odd if and only if
$\epsilon _{\mathfrak{t}}$
is odd if and only if
![]() $v(c_f)$
is odd, as
$v(c_f)$
is odd, as
![]() $\rho _{\mathfrak{t}}\in \mathbb{Z}$
. Now,
$\rho _{\mathfrak{t}}\in \mathbb{Z}$
. Now,
![]() $L_{\mathfrak{t}}^{w_h}$
gives some
$L_{\mathfrak{t}}^{w_h}$
gives some
![]() ${\mathbb{P}}^1$
s intersecting
${\mathbb{P}}^1$
s intersecting
![]() $\bar{X}_{F_{\mathfrak{t}}^{w_h}}\subset \mathcal{C}_{\Delta,s}^{w_h}$
. All these
$\bar{X}_{F_{\mathfrak{t}}^{w_h}}\subset \mathcal{C}_{\Delta,s}^{w_h}$
. All these
![]() ${\mathbb{P}}^1$
s are not in
${\mathbb{P}}^1$
s are not in
![]() $\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
(and so in
$\mathring{\mathcal{C}}_{\Delta,s}^{w_h}$
(and so in
![]() $\mathcal{C}_s$
) if and only if
$\mathcal{C}_s$
) if and only if
![]() $\mathfrak{t}_h\cup \mathfrak{t}_l=\mathfrak{t}$
. In particular,
$\mathfrak{t}_h\cup \mathfrak{t}_l=\mathfrak{t}$
. In particular,
![]() $\mathfrak{t}_h$
and
$\mathfrak{t}_h$
and
![]() $\mathfrak{t}_l$
are either both even or both odd. If
$\mathfrak{t}_l$
are either both even or both odd. If
![]() $\mathfrak{t}_h$
is even, then
$\mathfrak{t}_h$
is even, then
![]() $\gamma _{\mathfrak{t}_h}=2$
, and so the component given by
$\gamma _{\mathfrak{t}_h}=2$
, and so the component given by
![]() $V_{\mathfrak{t}_h}^{w_h}$
has multiplicity at least
$V_{\mathfrak{t}_h}^{w_h}$
has multiplicity at least
![]() $2$
. The self-intersection of
$2$
. The self-intersection of
![]() $\Gamma _{\mathfrak{t}}$
could not be
$\Gamma _{\mathfrak{t}}$
could not be
![]() $-1$
in this case. Assume
$-1$
in this case. Assume
![]() $\mathfrak{t}_h$
is odd. Let
$\mathfrak{t}_h$
is odd. Let
![]() $r\;:\!=\;r_{V_{\mathfrak{t}_h}^{w_h}}$
and consider
$r\;:\!=\;r_{V_{\mathfrak{t}_h}^{w_h}}$
and consider
given by
![]() $V_{\mathfrak{t}_h}^{w_h}$
. We want
$V_{\mathfrak{t}_h}^{w_h}$
. We want
![]() $d_r=1$
. Since
$d_r=1$
. Since
we have
![]() $d_{r+1}=2$
. As before
$d_{r+1}=2$
. As before
![]() $d_r=1$
if and only if
$d_r=1$
if and only if
![]() $\frac{\rho _{\mathfrak{t}_h}-\rho _{\mathfrak{t}}}{2}=\frac{n_0}{d_0}-\frac{n_{r+1}}{d_{r+1}}\geq \frac{1}{2}$
and similarly for
$\frac{\rho _{\mathfrak{t}_h}-\rho _{\mathfrak{t}}}{2}=\frac{n_0}{d_0}-\frac{n_{r+1}}{d_{r+1}}\geq \frac{1}{2}$
and similarly for
![]() $\mathfrak{t}_l$
. Thus if
$\mathfrak{t}_l$
. Thus if
![]() $\mathfrak{t}$
has two or more rational children and
$\mathfrak{t}$
has two or more rational children and
![]() $\Gamma _{\mathfrak{t}}$
is irreducible then it can be blown down if and only if
$\Gamma _{\mathfrak{t}}$
is irreducible then it can be blown down if and only if
![]() $v(c_f)$
is odd and
$v(c_f)$
is odd and
![]() $\mathfrak{t}=\mathfrak{R}$
is union of its
$\mathfrak{t}=\mathfrak{R}$
is union of its
![]() $2$
odd rational children
$2$
odd rational children
![]() $\mathfrak{t}_h$
and
$\mathfrak{t}_h$
and
![]() $\mathfrak{t}_l$
, satisfying
$\mathfrak{t}_l$
, satisfying
![]() $\rho _{\mathfrak{t}_h}\geq \rho _{\mathfrak{t}}+1$
,
$\rho _{\mathfrak{t}_h}\geq \rho _{\mathfrak{t}}+1$
,
![]() $\rho _{\mathfrak{t}_l}\geq \rho _{\mathfrak{t}}+1$
. This is case (3) of Definition 4.20.
$\rho _{\mathfrak{t}_l}\geq \rho _{\mathfrak{t}}+1$
. This is case (3) of Definition 4.20.
Suppose now
![]() $\Gamma _{\mathfrak{t}}$
reducible. By Proposition 5.21 the cluster
$\Gamma _{\mathfrak{t}}$
reducible. By Proposition 5.21 the cluster
![]() $\mathfrak{t}$
is übereven,
$\mathfrak{t}$
is übereven,
![]() $\epsilon _{\mathfrak{t}}$
is even and
$\epsilon _{\mathfrak{t}}$
is even and
![]() $\Gamma _{\mathfrak{t}}$
is the disjoint union of
$\Gamma _{\mathfrak{t}}$
is the disjoint union of
![]() $\Gamma _{\mathfrak{t}}^-\simeq{\mathbb{P}}^1$
and
$\Gamma _{\mathfrak{t}}^-\simeq{\mathbb{P}}^1$
and
![]() $\Gamma _{\mathfrak{t}}^+\simeq{\mathbb{P}}^1$
. As before, both
$\Gamma _{\mathfrak{t}}^+\simeq{\mathbb{P}}^1$
. As before, both
![]() $\Gamma _{\mathfrak{t}}^-$
and
$\Gamma _{\mathfrak{t}}^-$
and
![]() $\Gamma _{\mathfrak{t}}^+$
intersect at least other two components (given by the proper children of
$\Gamma _{\mathfrak{t}}^+$
intersect at least other two components (given by the proper children of
![]() $\mathfrak{t}$
). But then neither
$\mathfrak{t}$
). But then neither
![]() $\Gamma _{\mathfrak{t}}^-$
nor
$\Gamma _{\mathfrak{t}}^-$
nor
![]() $\Gamma _{\mathfrak{t}}^+$
has self-intersection
$\Gamma _{\mathfrak{t}}^+$
has self-intersection
![]() $-1$
, as
$-1$
, as
![]() $m_{\mathfrak{t}}=1$
.
$m_{\mathfrak{t}}=1$
.
We have showed that, for a rational cluster
![]() $\mathfrak{t}\in \Sigma _{K^{nr}}$
, an irreducible component of
$\mathfrak{t}\in \Sigma _{K^{nr}}$
, an irreducible component of
![]() $\Gamma _{\mathfrak{t}}$
can be blown down if and only if
$\Gamma _{\mathfrak{t}}$
can be blown down if and only if
![]() $\mathfrak{t}$
is contractible. Moreover, in this case,
$\mathfrak{t}$
is contractible. Moreover, in this case,
![]() $\Gamma _{\mathfrak{t}}$
is irreducible. It remains to show that after blowing down all components
$\Gamma _{\mathfrak{t}}$
is irreducible. It remains to show that after blowing down all components
![]() $\Gamma _{\mathfrak{t}}$
where
$\Gamma _{\mathfrak{t}}$
where
![]() $\mathfrak{t}$
is a contractible cluster, no other component can be blown down. First note that if
$\mathfrak{t}$
is a contractible cluster, no other component can be blown down. First note that if
![]() $\mathfrak{t}$
is a contractible cluster, then
$\mathfrak{t}$
is a contractible cluster, then
![]() $m_{\mathfrak{t}}=2$
and
$m_{\mathfrak{t}}=2$
and
![]() $\Gamma _{\mathfrak{t}}$
intersects one or two other components of multiplicity
$\Gamma _{\mathfrak{t}}$
intersects one or two other components of multiplicity
![]() $1$
at two points in total. If it intersects only one component, then after the blowing down, the latter will have a node and will not be isomorphic to
$1$
at two points in total. If it intersects only one component, then after the blowing down, the latter will have a node and will not be isomorphic to
![]() ${\mathbb{P}}^1$
. If
${\mathbb{P}}^1$
. If
![]() $\Gamma _{\mathfrak{t}}$
intersects two components and those intersect something else in
$\Gamma _{\mathfrak{t}}$
intersects two components and those intersect something else in
![]() $\mathcal{C}_s$
, then they will not have self-intersection
$\mathcal{C}_s$
, then they will not have self-intersection
![]() $-1$
also when
$-1$
also when
![]() $\Gamma _{\mathfrak{t}}$
is blown down. Therefore suppose that one of those two does not intersect any other component of
$\Gamma _{\mathfrak{t}}$
is blown down. Therefore suppose that one of those two does not intersect any other component of
![]() $\mathcal{C}_s$
. If we are in case (1) or case (2), it is easy to see that this never happens. Indeed, in those cases,
$\mathcal{C}_s$
. If we are in case (1) or case (2), it is easy to see that this never happens. Indeed, in those cases,
![]() $\Gamma _{\mathfrak{t}}$
intersects non-open-ended chains of
$\Gamma _{\mathfrak{t}}$
intersects non-open-ended chains of
![]() ${\mathbb{P}}^1$
s. Then without loss of generality assume to be in case (3) and that
${\mathbb{P}}^1$
s. Then without loss of generality assume to be in case (3) and that
![]() $\Gamma _{\mathfrak{t}_h}$
is the component that can be blown down once
$\Gamma _{\mathfrak{t}_h}$
is the component that can be blown down once
![]() $\Gamma _{\mathfrak{t}}$
has been contracted. This implies
$\Gamma _{\mathfrak{t}}$
has been contracted. This implies
![]() ${\mathfrak{s}}_h=\mathfrak{t}_h$
and
${\mathfrak{s}}_h=\mathfrak{t}_h$
and
![]() $\rho _{{\mathfrak{s}}_h}=\rho _{\mathfrak{t}}+1$
. Then
$\rho _{{\mathfrak{s}}_h}=\rho _{\mathfrak{t}}+1$
. Then
![]() $b_{{\mathfrak{s}}_h}=1$
and
$b_{{\mathfrak{s}}_h}=1$
and
![]() $\epsilon _{{\mathfrak{s}}_h}=\epsilon _{\mathfrak{t}}+|{\mathfrak{s}}_h|$
. Since both
$\epsilon _{{\mathfrak{s}}_h}=\epsilon _{\mathfrak{t}}+|{\mathfrak{s}}_h|$
. Since both
![]() $\epsilon _{\mathfrak{t}}$
and
$\epsilon _{\mathfrak{t}}$
and
![]() ${\mathfrak{s}}_h$
are odd, we have
${\mathfrak{s}}_h$
are odd, we have
![]() $\epsilon _{{\mathfrak{s}}_h}\in 2\mathbb{Z}$
. So
$\epsilon _{{\mathfrak{s}}_h}\in 2\mathbb{Z}$
. So
![]() $D_{{\mathfrak{s}}_h}=2$
and
$D_{{\mathfrak{s}}_h}=2$
and
![]() $\tilde{\mathfrak{s}}_h$
is the set of rational children of
$\tilde{\mathfrak{s}}_h$
is the set of rational children of
![]() ${\mathfrak{s}}_h$
. Hence
${\mathfrak{s}}_h$
. Hence
![]() $g({\mathfrak{s}}_h)=\left \lfloor \frac{|{\mathfrak{s}}_h|-1}{2}\right \rfloor \geq 1$
since
$g({\mathfrak{s}}_h)=\left \lfloor \frac{|{\mathfrak{s}}_h|-1}{2}\right \rfloor \geq 1$
since
![]() $|{\mathfrak{s}}_h|\geq 3$
. But then
$|{\mathfrak{s}}_h|\geq 3$
. But then
![]() $\Gamma _{{\mathfrak{s}}_h}$
cannot be blown down.
$\Gamma _{{\mathfrak{s}}_h}$
cannot be blown down.
5.12. Galois action
Consider the base extended hyperelliptic curve
![]() $C_{K^{nr}}/K^{nr}$
. The rational clusters of
$C_{K^{nr}}/K^{nr}$
. The rational clusters of
![]() $C_{K^{nr}}$
and their corresponding rational centres are then over
$C_{K^{nr}}$
and their corresponding rational centres are then over
![]() $K^{nr}$
. Denote
$K^{nr}$
. Denote
![]() $\Sigma _{K^{nr}}=\Sigma _{C_{K^{nr}}}^{\textrm{rat}}$
. For any proper cluster
$\Sigma _{K^{nr}}=\Sigma _{C_{K^{nr}}}^{\textrm{rat}}$
. For any proper cluster
![]() $\mathfrak{s}\in \Sigma _{K^{nr}}$
, let
$\mathfrak{s}\in \Sigma _{K^{nr}}$
, let
![]() $G_{\mathfrak{s}}=\textrm{Stab}_{G_K}(\mathfrak{s})$
,
$G_{\mathfrak{s}}=\textrm{Stab}_{G_K}(\mathfrak{s})$
,
![]() $K_{\mathfrak{s}}=\left ( K^{\textrm{s}}\right )^{G_{\mathfrak{s}}}$
and
$K_{\mathfrak{s}}=\left ( K^{\textrm{s}}\right )^{G_{\mathfrak{s}}}$
and
![]() $k_{\mathfrak{s}}$
be the residue field of
$k_{\mathfrak{s}}$
be the residue field of
![]() $K_{\mathfrak{s}}$
. Let
$K_{\mathfrak{s}}$
. Let
![]() $\Sigma _{C_{K^{nr}}}^{\textrm{min}}=\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}$
be the set of rationally minimal clusters of
$\Sigma _{C_{K^{nr}}}^{\textrm{min}}=\{{\mathfrak{s}}_1,\dots,{\mathfrak{s}}_m\}$
be the set of rationally minimal clusters of
![]() $C_{K^{nr}}$
. Fix a set
$C_{K^{nr}}$
. Fix a set
![]() $W=\{w_1,\dots,w_m\}\subset K^{nr}$
of corresponding rational centres. By Lemma A.1, we can assume this choice to be
$W=\{w_1,\dots,w_m\}\subset K^{nr}$
of corresponding rational centres. By Lemma A.1, we can assume this choice to be
![]() $G_K$
-equivariant, that is for any
$G_K$
-equivariant, that is for any
![]() $\sigma \in G_K$
, one has
$\sigma \in G_K$
, one has
![]() $\sigma (w_l)=w_h$
if and only if
$\sigma (w_l)=w_h$
if and only if
![]() $\sigma ({\mathfrak{s}}_l)={\mathfrak{s}}_h$
. We can also require that
$\sigma ({\mathfrak{s}}_l)={\mathfrak{s}}_h$
. We can also require that
![]() $w_h\in{\mathfrak{s}}_h$
if
$w_h\in{\mathfrak{s}}_h$
if
![]() ${\mathfrak{s}}_h\cap K_{{\mathfrak{s}}_h}\neq \varnothing$
. Similarly, for any proper cluster
${\mathfrak{s}}_h\cap K_{{\mathfrak{s}}_h}\neq \varnothing$
. Similarly, for any proper cluster
![]() $\mathfrak{t}\in \Sigma _{K^{nr}}\setminus \Sigma _{C_{K^{nr}}}^{\textrm{min}}$
, fix a rational centre
$\mathfrak{t}\in \Sigma _{K^{nr}}\setminus \Sigma _{C_{K^{nr}}}^{\textrm{min}}$
, fix a rational centre
![]() $w_{\mathfrak{t}}$
in such a way that
$w_{\mathfrak{t}}$
in such a way that
![]() $w_{\sigma (t)}=\sigma (w_{\mathfrak{t}})$
for any
$w_{\sigma (t)}=\sigma (w_{\mathfrak{t}})$
for any
![]() $\sigma \in G_K$
. Set
$\sigma \in G_K$
. Set
![]() $w_{{\mathfrak{s}}_o}\;:\!=\;w_o$
for any
$w_{{\mathfrak{s}}_o}\;:\!=\;w_o$
for any
![]() $o=1,\dots,m$
.
$o=1,\dots,m$
.
Lemma 5.22.
With the choices above, for any
![]() $h=1,\dots,m$
, the set of proper clusters in
$h=1,\dots,m$
, the set of proper clusters in
![]() $\Sigma _{C_{K^{nr}}}^{w_h}$
coincides with
$\Sigma _{C_{K^{nr}}}^{w_h}$
coincides with
![]() $\mathring{\Sigma }_{C_{K^{nr}}}^{w_h}$
.
$\mathring{\Sigma }_{C_{K^{nr}}}^{w_h}$
.
Proof. Suppose by contradiction that there exists a non-proper cluster
![]() $\{r\}=\mathfrak{s}\in \Sigma _{C_{K^{nr}}}^{w_h}$
, with
$\{r\}=\mathfrak{s}\in \Sigma _{C_{K^{nr}}}^{w_h}$
, with
![]() $r\neq w_h$
. Note that
$r\neq w_h$
. Note that
![]() $r\in{\mathfrak{s}}_h$
and so
$r\in{\mathfrak{s}}_h$
and so
![]() $\mathfrak{s}\lt{\mathfrak{s}}_h$
. Recall that since
$\mathfrak{s}\lt{\mathfrak{s}}_h$
. Recall that since
![]() $\mathfrak{s}$
is a cluster centred at
$\mathfrak{s}$
is a cluster centred at
![]() $w_h$
, it is cut out by the disc
$w_h$
, it is cut out by the disc
![]() $\mathcal{D}=\{x\in \bar{K}\mid v(x-w_h)\geq \rho _{\mathfrak{s}}^{w_h}\}$
, with
$\mathcal{D}=\{x\in \bar{K}\mid v(x-w_h)\geq \rho _{\mathfrak{s}}^{w_h}\}$
, with
![]() $\rho _{\mathfrak{s}}^{w_h}=v(r-w_h)\gt \rho _{{\mathfrak{s}}_h}$
. This implies that
$\rho _{\mathfrak{s}}^{w_h}=v(r-w_h)\gt \rho _{{\mathfrak{s}}_h}$
. This implies that
![]() $w_h\notin \mathfrak{R}$
, otherwise
$w_h\notin \mathfrak{R}$
, otherwise
![]() $w_h\in \mathfrak{s}$
and
$w_h\in \mathfrak{s}$
and
![]() $|\mathfrak{s}|\geq 2$
. In particular,
$|\mathfrak{s}|\geq 2$
. In particular,
![]() $w_h\notin{\mathfrak{s}}_h$
. For our choice of
$w_h\notin{\mathfrak{s}}_h$
. For our choice of
![]() $w_h$
, it follows that
$w_h$
, it follows that
![]() ${\mathfrak{s}}_h\cap K_{{\mathfrak{s}}_h}=\varnothing$
. Therefore
${\mathfrak{s}}_h\cap K_{{\mathfrak{s}}_h}=\varnothing$
. Therefore
![]() $r\notin K_{{\mathfrak{s}}_h}$
and so there exists
$r\notin K_{{\mathfrak{s}}_h}$
and so there exists
![]() $\sigma \in G_{{\mathfrak{s}}_h}$
such that
$\sigma \in G_{{\mathfrak{s}}_h}$
such that
![]() $\sigma (r)\neq r$
. Since
$\sigma (r)\neq r$
. Since
![]() $w_h\in K_{{\mathfrak{s}}_h}$
we have
$w_h\in K_{{\mathfrak{s}}_h}$
we have
But then
![]() $\sigma (r)\in \mathfrak{s}$
, and so
$\sigma (r)\in \mathfrak{s}$
, and so
![]() $|\mathfrak{s}|\geq 2$
, a contradiction.
$|\mathfrak{s}|\geq 2$
, a contradiction.
Assume that
![]() $C_{K^{nr}}$
is
$C_{K^{nr}}$
is
![]() $y$
-regular and has an almost rational cluster picture. By the previous lemma, from the set of rational centres
$y$
-regular and has an almost rational cluster picture. By the previous lemma, from the set of rational centres
![]() $W$
we can construct the proper regular model
$W$
we can construct the proper regular model
![]() $\mathcal{C}/O_{K^{nr}}$
of
$\mathcal{C}/O_{K^{nr}}$
of
![]() $C_{K^{nr}}$
as previously presented in this section. In this subsection we show how the Galois group
$C_{K^{nr}}$
as previously presented in this section. In this subsection we show how the Galois group
![]() $\textrm{Gal}(K^{nr}/K)$
acts on the
$\textrm{Gal}(K^{nr}/K)$
acts on the
![]() $O_{K^{nr}}$
-scheme
$O_{K^{nr}}$
-scheme
![]() $\mathcal{C}$
. Moreover, we describe the induced action of
$\mathcal{C}$
. Moreover, we describe the induced action of
![]() $G_k$
on the special fibre
$G_k$
on the special fibre
![]() $\mathcal{C}_s/k^{\textrm{s}}$
, and give defining equations for the principal components of
$\mathcal{C}_s/k^{\textrm{s}}$
, and give defining equations for the principal components of
![]() $\mathcal{C}_s$
compatibly with the action.
$\mathcal{C}_s$
compatibly with the action.
For any
![]() $l=1,\dots,m$
, recall the notation
$l=1,\dots,m$
, recall the notation
![]() $f_l(x)=f(x+w_l)\in K^{nr}[x]$
and
$f_l(x)=f(x+w_l)\in K^{nr}[x]$
and
![]() $C^{w_l}/K^{nr}\;:\;y^2=f_l(x)$
. Fix
$C^{w_l}/K^{nr}\;:\;y^2=f_l(x)$
. Fix
![]() $\sigma \in G_K$
. Let
$\sigma \in G_K$
. Let
![]() $l,h=1,\dots,m$
such that
$l,h=1,\dots,m$
such that
![]() $\sigma ({\mathfrak{s}}_l)={\mathfrak{s}}_h$
. Then
$\sigma ({\mathfrak{s}}_l)={\mathfrak{s}}_h$
. Then
![]() $\sigma (f_l)=f_h$
. Now, let
$\sigma (f_l)=f_h$
. Now, let
![]() $\mathfrak{t}\in \Sigma _{C_{K^{nr}}}^{w_l}$
be a proper cluster. Then
$\mathfrak{t}\in \Sigma _{C_{K^{nr}}}^{w_l}$
be a proper cluster. Then
![]() $\sigma (\mathfrak{t})\in \Sigma _{C_{K^{nr}}}^{w_h}$
and
$\sigma (\mathfrak{t})\in \Sigma _{C_{K^{nr}}}^{w_h}$
and
![]() $\rho _{\mathfrak{t}}=\rho _{\sigma (\mathfrak{t})}$
. It follows that most of the quantities attached to
$\rho _{\mathfrak{t}}=\rho _{\sigma (\mathfrak{t})}$
. It follows that most of the quantities attached to
![]() $\mathfrak{t}$
, such as those of Definition 4.6, are the same for
$\mathfrak{t}$
, such as those of Definition 4.6, are the same for
![]() $\sigma (\mathfrak{t})$
, for example
$\sigma (\mathfrak{t})$
, for example
![]() $\epsilon _{\mathfrak{t}}=\epsilon _{\sigma (\mathfrak{t})}$
. In particular, if
$\epsilon _{\mathfrak{t}}=\epsilon _{\sigma (\mathfrak{t})}$
. In particular, if
![]() $M$
is a matrix associated to
$M$
is a matrix associated to
![]() $\mathfrak{t}$
then
$\mathfrak{t}$
then
![]() $M$
is associated to
$M$
is associated to
![]() $\sigma (\mathfrak{t})$
as well. So
$\sigma (\mathfrak{t})$
as well. So
![]() $\sigma (\mathcal{F}_M^l)=\mathcal{F}_{M}^h$
. Finally, as
$\sigma (\mathcal{F}_M^l)=\mathcal{F}_{M}^h$
. Finally, as
![]() $\sigma (\prod _{o\neq l}(x+w_{lo})^{-1})=\prod _{o\neq h}(x+w_{ho})^{-1}$
we also have
$\sigma (\prod _{o\neq l}(x+w_{lo})^{-1})=\prod _{o\neq h}(x+w_{ho})^{-1}$
we also have
![]() $\sigma (T_M^l)=T_{M}^h$
.
$\sigma (T_M^l)=T_{M}^h$
.
Hence the natural
![]() $K^{nr}$
-isomorphism
$K^{nr}$
-isomorphism
![]() $C^{w_h}\xrightarrow{\sigma }C^{w_l}$
induces
$C^{w_h}\xrightarrow{\sigma }C^{w_l}$
induces
![]() $O_{K^{nr}}$
-isomorphisms of schemes
$O_{K^{nr}}$
-isomorphisms of schemes
Via the glueing morphisms (4), these maps describe the action of
![]() $G_K$
on
$G_K$
on
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
We want to study the action of
![]() $G_k$
on the special fibre of
$G_k$
on the special fibre of
![]() $\mathcal{C}$
more in detail. Let
$\mathcal{C}$
more in detail. Let
![]() $\sigma \in \textrm{Gal}(K^{nr}/K)$
and let
$\sigma \in \textrm{Gal}(K^{nr}/K)$
and let
![]() $\bar \sigma \in G_k$
corresponding to
$\bar \sigma \in G_k$
corresponding to
![]() $\sigma$
via the canonical isomorphism
$\sigma$
via the canonical isomorphism
![]() $\textrm{Gal}(K^{nr}/K)\simeq G_k$
. Let
$\textrm{Gal}(K^{nr}/K)\simeq G_k$
. Let
![]() $l,h$
and
$l,h$
and
![]() $\mathfrak{t}$
as above. In Section 5.6 we described closed
$\mathfrak{t}$
as above. In Section 5.6 we described closed
![]() $1$
-dimensional subschemes composing
$1$
-dimensional subschemes composing
![]() $\mathring{\mathcal{C}}_{\Delta,s}^{w_l}$
and the morphisms induced by the glueing maps. Recall the polynomials introduced in Definition 5.12. From (10) we get
$\mathring{\mathcal{C}}_{\Delta,s}^{w_l}$
and the morphisms induced by the glueing maps. Recall the polynomials introduced in Definition 5.12. From (10) we get
From the equality (7) we obtain
![]() $\bar \sigma (f_{\mathfrak{t},w_l})=f_{\sigma (\mathfrak{t}),w_h}$
. Note that the previous relations can also be recovered directly from the definitions.
$\bar \sigma (f_{\mathfrak{t},w_l})=f_{\sigma (\mathfrak{t}),w_h}$
. Note that the previous relations can also be recovered directly from the definitions.
Lemma 5.23.
Let
![]() $w_{\mathfrak{t}}$
be the rational centre of
$w_{\mathfrak{t}}$
be the rational centre of
![]() $\mathfrak{t}$
fixed above. Then
$\mathfrak{t}$
fixed above. Then
-
(i)
 $\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}},\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}\in k_{\mathfrak{t}}[X]$
;
$\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}},\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}\in k_{\mathfrak{t}}[X]$
; -
(ii)
 $\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}}=\overline{g_{\mathfrak{t},w_l}}$
and
$\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}}=\overline{g_{\mathfrak{t},w_l}}$
and
 $ \overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}(X)=\overline{f_{\mathfrak{t},w_l}}(X+\overline{u_{w_{\mathfrak{t}} w_l}})$
where
$ \overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}(X)=\overline{f_{\mathfrak{t},w_l}}(X+\overline{u_{w_{\mathfrak{t}} w_l}})$
where
 $\overline{u_{w_{\mathfrak{t}} w_l}}=\tfrac{w_{\mathfrak{t}}-w_l}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
;
$\overline{u_{w_{\mathfrak{t}} w_l}}=\tfrac{w_{\mathfrak{t}}-w_l}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
;
Proof. For any rational centre
![]() $w$
of
$w$
of
![]() $\mathfrak{t}$
, let
$\mathfrak{t}$
, let
![]() $u_{\mathfrak{t},w}=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \mathfrak{t}} (w-r)$
as in Definition 5.12. Note that
$u_{\mathfrak{t},w}=c_f\textstyle \prod _{r\in \mathfrak{R}\setminus \mathfrak{t}} (w-r)$
as in Definition 5.12. Note that
![]() $u_{\mathfrak{t},w}/\pi ^{v(u_{\mathfrak{t},w})}$
is independent of
$u_{\mathfrak{t},w}/\pi ^{v(u_{\mathfrak{t},w})}$
is independent of
![]() $w$
since
$w$
since
for any
![]() $r\in \mathfrak{R}\setminus \mathfrak{t}$
. Then
$r\in \mathfrak{R}\setminus \mathfrak{t}$
. Then
![]() $\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}}=\overline{g_{\mathfrak{t},w_l}}$
. If
$\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}}=\overline{g_{\mathfrak{t},w_l}}$
. If
![]() $\bar \sigma \in \textrm{Gal}(k^{\textrm{s}}/k_{\mathfrak{t}})$
, i.e.
$\bar \sigma \in \textrm{Gal}(k^{\textrm{s}}/k_{\mathfrak{t}})$
, i.e.
![]() $\sigma \in \textrm{Gal}(K^{nr}/K_{\mathfrak{t}})$
, then
$\sigma \in \textrm{Gal}(K^{nr}/K_{\mathfrak{t}})$
, then
In particular
![]() $\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}}\in k_{\mathfrak{t}}[X]$
.
$\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}}\in k_{\mathfrak{t}}[X]$
.
Since
![]() $u_{\mathfrak{t},w}/\pi ^{v(u_{\mathfrak{t},w})}$
is independent of
$u_{\mathfrak{t},w}/\pi ^{v(u_{\mathfrak{t},w})}$
is independent of
![]() $w$
we also have
$w$
we also have
Suppose
![]() $\rho _{\mathfrak{t}}\in \mathbb{Z}$
. Then
$\rho _{\mathfrak{t}}\in \mathbb{Z}$
. Then
![]() $b_{\mathfrak{t}}=1$
and so the equality above implies
$b_{\mathfrak{t}}=1$
and so the equality above implies
![]() $\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}(X)=\overline{f_{\mathfrak{t},w_l}}(X+{\overline{u_{w_{\mathfrak{t}} w_l}}})$
. Suppose
$\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}(X)=\overline{f_{\mathfrak{t},w_l}}(X+{\overline{u_{w_{\mathfrak{t}} w_l}}})$
. Suppose
![]() $\rho \notin \mathbb{Z}$
. Then
$\rho \notin \mathbb{Z}$
. Then
![]() $v(w-w_{\mathfrak{t}})\gt \rho _{\mathfrak{t}}$
for any rational centre
$v(w-w_{\mathfrak{t}})\gt \rho _{\mathfrak{t}}$
for any rational centre
![]() $w$
of
$w$
of
![]() $\mathfrak{t}$
as
$\mathfrak{t}$
as
![]() $v(w-w_{\mathfrak{t}})\in \mathbb{Z}$
and
$v(w-w_{\mathfrak{t}})\in \mathbb{Z}$
and
![]() $v(w-w_{\mathfrak{t}})\geq \rho _{\mathfrak{t}}$
. Hence
$v(w-w_{\mathfrak{t}})\geq \rho _{\mathfrak{t}}$
. Hence
![]() ${\overline{u_{w_{\mathfrak{t}} w_l}}}=0$
. Thus
${\overline{u_{w_{\mathfrak{t}} w_l}}}=0$
. Thus
![]() $\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}(X^{b_{\mathfrak{t}}})=\overline{f_{\mathfrak{t},w_l}}(X^{b_{\mathfrak{t}}})$
, which implies
$\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}(X^{b_{\mathfrak{t}}})=\overline{f_{\mathfrak{t},w_l}}(X^{b_{\mathfrak{t}}})$
, which implies
![]() $\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}(X)=\overline{f_{\mathfrak{t},w_l}}(X)=\overline{f_{\mathfrak{t},w_l}}(X+{\overline{u_{w_{\mathfrak{t}} w_l}}})$
. If
$\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}(X)=\overline{f_{\mathfrak{t},w_l}}(X)=\overline{f_{\mathfrak{t},w_l}}(X+{\overline{u_{w_{\mathfrak{t}} w_l}}})$
. If
![]() $\bar \sigma \in \textrm{Gal}(k^{\textrm{s}}/k_{\mathfrak{t}})$
, i.e.
$\bar \sigma \in \textrm{Gal}(k^{\textrm{s}}/k_{\mathfrak{t}})$
, i.e.
![]() $\sigma \in \textrm{Gal}(K^{nr}/K_{\mathfrak{t}})$
, then
$\sigma \in \textrm{Gal}(K^{nr}/K_{\mathfrak{t}})$
, then
and so
![]() $\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}\in k_{\mathfrak{t}}[X]$
.
$\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}\in k_{\mathfrak{t}}[X]$
.
Remark 5.24.
Note that the polynomials
![]() $\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}$
,
$\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}$
,
![]() $\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}}$
and
$\overline{g_{\mathfrak{t},w_{\mathfrak{t}}}}$
and
![]() $\overline{g_{{\mathfrak{s}}_h,w_h}^0}$
equal the polynomials
$\overline{g_{{\mathfrak{s}}_h,w_h}^0}$
equal the polynomials
![]() $\overline{f_{\mathfrak{t}}}$
,
$\overline{f_{\mathfrak{t}}}$
,
![]() $\overline{g_{\mathfrak{t}}}$
and
$\overline{g_{\mathfrak{t}}}$
and
![]() $\overline{g_{{\mathfrak{s}}_h}^0}$
given in Definition 4.22
.
$\overline{g_{{\mathfrak{s}}_h}^0}$
given in Definition 4.22
.
Let
![]() $V=V_{\mathfrak{t}}^{w_l}$
and consider the subscheme
$V=V_{\mathfrak{t}}^{w_l}$
and consider the subscheme
![]() $X_V\times{\mathbb{P}}_V$
of
$X_V\times{\mathbb{P}}_V$
of
![]() $\mathcal{C}_s$
given by
$\mathcal{C}_s$
given by
![]() $V$
, where
$V$
, where
![]() ${\mathbb{P}}_V$
is a chain of
${\mathbb{P}}_V$
is a chain of
![]() ${\mathbb{P}}^1$
s and
${\mathbb{P}}^1$
s and
![]() $X_V\;:\;\{\overline{g_{\mathfrak{t},w_l}}=0\}$
over
$X_V\;:\;\{\overline{g_{\mathfrak{t},w_l}}=0\}$
over
![]() ${\mathbb{G}}_{m,k^{\textrm{s}}}$
. If
${\mathbb{G}}_{m,k^{\textrm{s}}}$
. If
![]() ${\mathfrak{s}}_h\subset \mathfrak{t}$
, then the glueing map
${\mathfrak{s}}_h\subset \mathfrak{t}$
, then the glueing map
![]() $U_M^h\rightarrow U_M^l$
induces the identity
$U_M^h\rightarrow U_M^l$
induces the identity
![]() $\phi _V^{hl}\;:\;X_{V_{\mathfrak{t}}^{w_h}}\xrightarrow{=}X_{V_{\mathfrak{t}}^{w_l}}$
. Define
$\phi _V^{hl}\;:\;X_{V_{\mathfrak{t}}^{w_h}}\xrightarrow{=}X_{V_{\mathfrak{t}}^{w_l}}$
. Define
![]() $X_{\mathfrak{t}}\subseteq{\mathbb{G}}_{m,k^{\textrm{s}}}$
given by
$X_{\mathfrak{t}}\subseteq{\mathbb{G}}_{m,k^{\textrm{s}}}$
given by
![]() $g_{\mathfrak{t},w_{\mathfrak{t}}}=0$
. By Lemma 5.23,
$g_{\mathfrak{t},w_{\mathfrak{t}}}=0$
. By Lemma 5.23,
![]() $\phi _V^o\;:\;X_{\mathfrak{t}}\xrightarrow{\simeq } X_{V_{\mathfrak{t}}^{w_o}}$
, for
$\phi _V^o\;:\;X_{\mathfrak{t}}\xrightarrow{\simeq } X_{V_{\mathfrak{t}}^{w_o}}$
, for
![]() $o=h,l$
, and this isomorphism is compatible with the Galois action and the glueing maps, that is
$o=h,l$
, and this isomorphism is compatible with the Galois action and the glueing maps, that is
![]() $\sigma \circ \phi _V^h=\phi _V^l\circ \sigma$
and
$\sigma \circ \phi _V^h=\phi _V^l\circ \sigma$
and
![]() $\phi _V^{hl}\circ \phi _V^h=\phi _V^l$
as morphisms on
$\phi _V^{hl}\circ \phi _V^h=\phi _V^l$
as morphisms on
![]() $X_{\mathfrak{t}}$
.
$X_{\mathfrak{t}}$
.
When
![]() $V_0=V_0^{w_l}$
we can consider the subscheme
$V_0=V_0^{w_l}$
we can consider the subscheme
![]() $X_{V_0}\times{\mathbb{P}}_{V_0}$
given by
$X_{V_0}\times{\mathbb{P}}_{V_0}$
given by
![]() $V_0$
, where
$V_0$
, where
![]() ${\mathbb{P}}_{V_0}$
is a chain of
${\mathbb{P}}_{V_0}$
is a chain of
![]() ${\mathbb{P}}^1$
s and
${\mathbb{P}}^1$
s and
![]() $X_{V_0}\;:\;\{\overline{g_{{\mathfrak{s}}_l,w_l}}=0\}$
over
$X_{V_0}\;:\;\{\overline{g_{{\mathfrak{s}}_l,w_l}}=0\}$
over
![]() ${\mathbb{G}}_{m,k^{\textrm{s}}}$
. Since
${\mathbb{G}}_{m,k^{\textrm{s}}}$
. Since
![]() $X_{V_0}\times{\mathbb{P}}_{V_0}$
is never glued to any other component there is no need to choose a different model for it.
$X_{V_0}\times{\mathbb{P}}_{V_0}$
is never glued to any other component there is no need to choose a different model for it.
Let
![]() $L=L_{\mathfrak{t}}^{w_l}$
and consider the subscheme
$L=L_{\mathfrak{t}}^{w_l}$
and consider the subscheme
![]() $X_{L}^W\times{\mathbb{P}}_{L}$
given by
$X_{L}^W\times{\mathbb{P}}_{L}$
given by
![]() $L$
, where
$L$
, where
![]() ${\mathbb{P}}_{L}$
is a chain of
${\mathbb{P}}_{L}$
is a chain of
![]() ${\mathbb{P}}^1$
s and
${\mathbb{P}}^1$
s and
![]() $X_{L}^W\;:\;\{\overline{f_{\mathfrak{t},w_l}}=0\}$
over
$X_{L}^W\;:\;\{\overline{f_{\mathfrak{t},w_l}}=0\}$
over
![]() ${\mathbb{A}}^1_{k^{\textrm{s}}}$
. If
${\mathbb{A}}^1_{k^{\textrm{s}}}$
. If
![]() ${\mathfrak{s}}_h\subset \mathfrak{t}$
, then the isomorphism
${\mathfrak{s}}_h\subset \mathfrak{t}$
, then the isomorphism
![]() $\phi _L^{hl}\;:\;X_{L_{\mathfrak{t}}^{w_h}}^W\xrightarrow{\simeq } X_{L_{\mathfrak{t}}^{w_l}}^W$
given by the glueing map
$\phi _L^{hl}\;:\;X_{L_{\mathfrak{t}}^{w_h}}^W\xrightarrow{\simeq } X_{L_{\mathfrak{t}}^{w_l}}^W$
given by the glueing map
![]() $U_M^h\rightarrow U_M^l$
is induced by the ring isomorphism
$U_M^h\rightarrow U_M^l$
is induced by the ring isomorphism
![]() $k^{\textrm{s}}[X]\rightarrow k^{\textrm{s}}[X]$
, sending
$k^{\textrm{s}}[X]\rightarrow k^{\textrm{s}}[X]$
, sending
![]() $X\mapsto X+\overline{u_{w_hw_l}}$
, where
$X\mapsto X+\overline{u_{w_hw_l}}$
, where
![]() $\overline{u_{w_hw_l}}=\frac{w_h-w_l}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
. Define
$\overline{u_{w_hw_l}}=\frac{w_h-w_l}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
. Define
![]() $X_{\mathfrak{t}}^W\subseteq{\mathbb{A}}^1_{k^{\textrm{s}}}$
given by
$X_{\mathfrak{t}}^W\subseteq{\mathbb{A}}^1_{k^{\textrm{s}}}$
given by
![]() ${\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}}=0$
. By Lemma 5.23, the map
${\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}}=0$
. By Lemma 5.23, the map
![]() $X\mapsto X+\overline{u_{w_{\mathfrak{t}} w_l}}$
induces an isomorphism
$X\mapsto X+\overline{u_{w_{\mathfrak{t}} w_l}}$
induces an isomorphism
![]() $\phi _L^o\;:\;X_{\mathfrak{t}}^W\xrightarrow{\simeq } X_{L_{\mathfrak{t}}^{w_o}}^W$
, for
$\phi _L^o\;:\;X_{\mathfrak{t}}^W\xrightarrow{\simeq } X_{L_{\mathfrak{t}}^{w_o}}^W$
, for
![]() $o=h,l$
, compatible with the Galois action and the glueing morphisms, that is
$o=h,l$
, compatible with the Galois action and the glueing morphisms, that is
![]() $\sigma \circ \phi _L^h=\phi _L^l\circ \sigma$
and
$\sigma \circ \phi _L^h=\phi _L^l\circ \sigma$
and
![]() $\phi _L^{hl}\circ \phi _L^h=\phi _L^l$
as morphisms on
$\phi _L^{hl}\circ \phi _L^h=\phi _L^l$
as morphisms on
![]() $X_{\mathfrak{t}}^W$
.
$X_{\mathfrak{t}}^W$
.
Recall the definitions of
![]() $\hat{\mathfrak{t}}^W$
and
$\hat{\mathfrak{t}}^W$
and
![]() ${\mathbb{G}}_{\mathfrak{t},w_l}\subseteq{\mathbb{A}}_{k^{\textrm{s}}}^1$
given in Definition 5.15 and the definition of
${\mathbb{G}}_{\mathfrak{t},w_l}\subseteq{\mathbb{A}}_{k^{\textrm{s}}}^1$
given in Definition 5.15 and the definition of
![]() $\mathfrak{t}$
given in Definition 4.22. Note that by Lemma 5.22,
$\mathfrak{t}$
given in Definition 4.22. Note that by Lemma 5.22,
Fix
![]() $c=0,\dots,b_{\mathfrak{t}}-1$
such that
$c=0,\dots,b_{\mathfrak{t}}-1$
such that
![]() $1/b_{\mathfrak{t}}-c\rho _{\mathfrak{t}}\in \mathbb{Z}$
. For any rational centre
$1/b_{\mathfrak{t}}-c\rho _{\mathfrak{t}}\in \mathbb{Z}$
. For any rational centre
![]() $w\in K^{nr}$
of
$w\in K^{nr}$
of
![]() $\mathfrak{t}$
define
$\mathfrak{t}$
define
![]() $\hat{f}_{\mathfrak{t},w}\in k^{\textrm{s}}[X,Y]$
by
$\hat{f}_{\mathfrak{t},w}\in k^{\textrm{s}}[X,Y]$
by
where
![]() ${\overline{u_{w_{\mathfrak{s}} w}}}=\tfrac{w_{\mathfrak{s}}-w}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
(
${\overline{u_{w_{\mathfrak{s}} w}}}=\tfrac{w_{\mathfrak{s}}-w}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
(
![]() $w_{\mathfrak{s}}=w_l$
if
$w_{\mathfrak{s}}=w_l$
if
![]() $\mathfrak{s}=\varnothing$
). Let
$\mathfrak{s}=\varnothing$
). Let
![]() $L=L_{\mathfrak{t}}^{w_l}$
,
$L=L_{\mathfrak{t}}^{w_l}$
,
![]() $F=F_{\mathfrak{t}}^{w_l}$
and
$F=F_{\mathfrak{t}}^{w_l}$
and
![]() $M=M_{L,0}$
. It follows from Lemma 5.17 that the scheme
$M=M_{L,0}$
. It follows from Lemma 5.17 that the scheme
![]() $\Gamma _{\mathfrak{t}}^{w_l}={X}_F\cap U_M^{l}$
is given by
$\Gamma _{\mathfrak{t}}^{w_l}={X}_F\cap U_M^{l}$
is given by
![]() $Y^{D_{\mathfrak{t}}}=\hat{f}_{\mathfrak{t},w_l}(X)$
as a subscheme of
$Y^{D_{\mathfrak{t}}}=\hat{f}_{\mathfrak{t},w_l}(X)$
as a subscheme of
![]() ${\mathbb{G}}_{\mathfrak{t},w_l}\times{\mathbb{A}}_{k^{\textrm{s}}}^1$
. We then obtain
${\mathbb{G}}_{\mathfrak{t},w_l}\times{\mathbb{A}}_{k^{\textrm{s}}}^1$
. We then obtain
![]() $\bar \sigma (\hat{f}_{\mathfrak{t},w_l})=\hat{f}_{\sigma (\mathfrak{t}),w_h}$
from the action (10) of
$\bar \sigma (\hat{f}_{\mathfrak{t},w_l})=\hat{f}_{\sigma (\mathfrak{t}),w_h}$
from the action (10) of
![]() $\sigma$
on
$\sigma$
on
![]() $U_M^l$
.
$U_M^l$
.
Lemma 5.25. With the notation above,
-
(i)
 $\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}\in k_{\mathfrak{t}}[X]$
;
$\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}\in k_{\mathfrak{t}}[X]$
; -
(ii)
 $\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}(X)=\hat{f}_{\mathfrak{t},w_l}(X+{\overline{u_{w_{\mathfrak{t}} w_l}}})$
where
$\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}(X)=\hat{f}_{\mathfrak{t},w_l}(X+{\overline{u_{w_{\mathfrak{t}} w_l}}})$
where
 $\overline{u_{w_{\mathfrak{t}} w_l}}=\tfrac{w_{\mathfrak{t}}-w_l}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
;
$\overline{u_{w_{\mathfrak{t}} w_l}}=\tfrac{w_{\mathfrak{t}}-w_l}{\pi ^{\rho _{\mathfrak{t}}}}\mod \pi$
;
Proof. If
![]() $\mathfrak{s}\in \mathfrak{t}$
, then
$\mathfrak{s}\in \mathfrak{t}$
, then
![]() $\sigma (\mathfrak{s})\in{(\sigma (\mathfrak{t}))}$
and
$\sigma (\mathfrak{s})\in{(\sigma (\mathfrak{t}))}$
and
![]() $\bar \sigma ({\overline{u_{w_{\mathfrak{s}} w}}})={\overline{u_{w_{\sigma (\mathfrak{s})}\sigma (w)}}}$
for any rational centre
$\bar \sigma ({\overline{u_{w_{\mathfrak{s}} w}}})={\overline{u_{w_{\sigma (\mathfrak{s})}\sigma (w)}}}$
for any rational centre
![]() $w$
of
$w$
of
![]() $\mathfrak{t}$
. Hence
$\mathfrak{t}$
. Hence
![]() $\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}\in k_{\mathfrak{t}}[X]$
and
$\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}\in k_{\mathfrak{t}}[X]$
and
![]() $\bar \sigma (\hat{f}_{\mathfrak{t},w_l})=\hat{f}_{\sigma (\mathfrak{t}),w_h}$
by Lemma 5.23(i),(iii). Since
$\bar \sigma (\hat{f}_{\mathfrak{t},w_l})=\hat{f}_{\sigma (\mathfrak{t}),w_h}$
by Lemma 5.23(i),(iii). Since
![]() ${\overline{u_{w_{\mathfrak{s}} w_{\mathfrak{t}}}}}={\overline{u_{w_{\mathfrak{s}} w_l}}}-{\overline{u_{w_{\mathfrak{t}} w_l}}}$
, Lemma 5.23(ii) implies
${\overline{u_{w_{\mathfrak{s}} w_{\mathfrak{t}}}}}={\overline{u_{w_{\mathfrak{s}} w_l}}}-{\overline{u_{w_{\mathfrak{t}} w_l}}}$
, Lemma 5.23(ii) implies
![]() $\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}(X)=\hat{f}_{\mathfrak{t},w_l}(X+{\overline{u_{w_{\mathfrak{t}} w_l}}})$
.
$\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}(X)=\hat{f}_{\mathfrak{t},w_l}(X+{\overline{u_{w_{\mathfrak{t}} w_l}}})$
.
Define
![]() $\Gamma _{\mathfrak{t}}^{w_{\mathfrak{t}}}\subset{\mathbb{G}}_{\mathfrak{t},w_{\mathfrak{t}}}\times{\mathbb{A}}^1_{k^{\textrm{s}}}$
given by
$\Gamma _{\mathfrak{t}}^{w_{\mathfrak{t}}}\subset{\mathbb{G}}_{\mathfrak{t},w_{\mathfrak{t}}}\times{\mathbb{A}}^1_{k^{\textrm{s}}}$
given by
![]() $Y^{D_{\mathfrak{t}}}=\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}$
. Suppose
$Y^{D_{\mathfrak{t}}}=\hat{f}_{\mathfrak{t},w_{\mathfrak{t}}}$
. Suppose
![]() ${\mathfrak{s}}_h\subset \mathfrak{t}$
, and let
${\mathfrak{s}}_h\subset \mathfrak{t}$
, and let
![]() $\phi _{\mathfrak{t}}^{hl}\;:\;\Gamma _{\mathfrak{t}}^{w_h}\simeq \Gamma _{\mathfrak{t}}^{w_l}$
be the isomorphism coming from the glueing map
$\phi _{\mathfrak{t}}^{hl}\;:\;\Gamma _{\mathfrak{t}}^{w_h}\simeq \Gamma _{\mathfrak{t}}^{w_l}$
be the isomorphism coming from the glueing map
![]() $U_M^h\rightarrow U_M^l$
induced by the ring homomorphism
$U_M^h\rightarrow U_M^l$
induced by the ring homomorphism
![]() $X\mapsto X+\overline{u_{w_hw_l}}$
. By Lemma 5.25, the map
$X\mapsto X+\overline{u_{w_hw_l}}$
. By Lemma 5.25, the map
![]() $X\mapsto X+\overline{u_{w_{\mathfrak{t}} w_l}}$
induces an isomorphism
$X\mapsto X+\overline{u_{w_{\mathfrak{t}} w_l}}$
induces an isomorphism
![]() $\phi _{\mathfrak{t}}^o:\Gamma _{\mathfrak{t}}^{w_{\mathfrak{t}}}\simeq \Gamma _{\mathfrak{t}}^{w_o}$
, for
$\phi _{\mathfrak{t}}^o:\Gamma _{\mathfrak{t}}^{w_{\mathfrak{t}}}\simeq \Gamma _{\mathfrak{t}}^{w_o}$
, for
![]() $o=h,l$
, which is compatible with the Galois action and the glueing maps, that is
$o=h,l$
, which is compatible with the Galois action and the glueing maps, that is
![]() $\sigma \circ \phi _{\mathfrak{t}}^h=\phi _{\mathfrak{t}}^l\circ \sigma$
and
$\sigma \circ \phi _{\mathfrak{t}}^h=\phi _{\mathfrak{t}}^l\circ \sigma$
and
![]() $\phi _{\mathfrak{t}}^{hl}\circ \phi _{\mathfrak{t}}^h=\phi _{\mathfrak{t}}^l$
as morphisms on
$\phi _{\mathfrak{t}}^{hl}\circ \phi _{\mathfrak{t}}^h=\phi _{\mathfrak{t}}^l$
as morphisms on
![]() $\Gamma _{\mathfrak{t}}^{w_{\mathfrak{t}}}$
. Therefore
$\Gamma _{\mathfrak{t}}^{w_{\mathfrak{t}}}$
. Therefore
![]() $\Gamma _{\mathfrak{t}}$
is isomorphic to the smooth completion of
$\Gamma _{\mathfrak{t}}$
is isomorphic to the smooth completion of
![]() $\Gamma _{\mathfrak{t}}^{w_{\mathfrak{t}}}$
, and so it is given by
$\Gamma _{\mathfrak{t}}^{w_{\mathfrak{t}}}$
, and so it is given by
![]() $Y^{D_{\mathfrak{t}}}=\tilde{f}_{\mathfrak{t}}(X)$
, where
$Y^{D_{\mathfrak{t}}}=\tilde{f}_{\mathfrak{t}}(X)$
, where
![]() $\tilde{f}_{\mathfrak{t}}(X)=\prod _{\mathfrak{s}\in \mathfrak{t}}(X-{\overline{u_{w_{\mathfrak{s}} w_{\mathfrak{t}}}}}){\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}}(X)$
is the polynomial given in Definition 4.22.
$\tilde{f}_{\mathfrak{t}}(X)=\prod _{\mathfrak{s}\in \mathfrak{t}}(X-{\overline{u_{w_{\mathfrak{s}} w_{\mathfrak{t}}}}}){\overline{f_{\mathfrak{t},w_{\mathfrak{t}}}}}(X)$
is the polynomial given in Definition 4.22.
6. Integral differentials
Let
![]() $C$
be a hyperelliptic curve of genus
$C$
be a hyperelliptic curve of genus
![]() $g\geq 1$
defined over
$g\geq 1$
defined over
![]() $K$
by a Weierstrass equation
$K$
by a Weierstrass equation
![]() $y^2=f(x)$
. It is well-known that the
$y^2=f(x)$
. It is well-known that the
![]() $K$
-vector space of global sections of the sheaf of differentials of
$K$
-vector space of global sections of the sheaf of differentials of
![]() $C$
, namely
$C$
, namely
![]() $H^0(C,\Omega ^1_{C/K})$
, is spanned by the basis
$H^0(C,\Omega ^1_{C/K})$
, is spanned by the basis
Let
![]() $\mathcal{C}$
be a regular model of
$\mathcal{C}$
be a regular model of
![]() $C$
over
$C$
over
![]() $O_K$
and consider its canonical (or dualising) sheaf
$O_K$
and consider its canonical (or dualising) sheaf
![]() $\omega _{\mathcal{C}/O_K}$
. The free
$\omega _{\mathcal{C}/O_K}$
. The free
![]() $O_K$
-module of its global sections
$O_K$
-module of its global sections
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
can be viewed as an
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
can be viewed as an
![]() $O_K$
-lattice in
$O_K$
-lattice in
![]() $H^0(C,\Omega ^1_{C/K})$
(see [Reference Liu9, Corollary 9.2.25(a)]). The aim of this section is to present a basis of
$H^0(C,\Omega ^1_{C/K})$
(see [Reference Liu9, Corollary 9.2.25(a)]). The aim of this section is to present a basis of
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
as an
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
as an
![]() $O_K$
-linear combination of the elements in
$O_K$
-linear combination of the elements in
![]() $\underline{\omega }$
under the assumptions of Theorem 4.23. Note that by [Reference Liu9, Corollary 9.2.25(b)] the problem is independent of the choice of model
$\underline{\omega }$
under the assumptions of Theorem 4.23. Note that by [Reference Liu9, Corollary 9.2.25(b)] the problem is independent of the choice of model
![]() $\mathcal{C}$
but it does depend on the choice of the equation
$\mathcal{C}$
but it does depend on the choice of the equation
![]() $y^2=f(x)$
since the basis
$y^2=f(x)$
since the basis
![]() $\underline{\omega }$
does. Throughout this section let
$\underline{\omega }$
does. Throughout this section let
![]() $C$
and
$C$
and
![]() $\mathcal{C}/O_K$
be as above.
$\mathcal{C}/O_K$
be as above.
If
![]() $C$
is
$C$
is
![]() $\Delta _v$
-regular, [Reference Dokchitser1, Theorem 8.12] gives an
$\Delta _v$
-regular, [Reference Dokchitser1, Theorem 8.12] gives an
![]() $O_K$
-basis of
$O_K$
-basis of
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
, as required. We rephrase it in terms of rational cluster invariants, by using results of Section 3 and Lemma 4.12.
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
, as required. We rephrase it in terms of rational cluster invariants, by using results of Section 3 and Lemma 4.12.
Theorem 6.1.
Suppose
![]() $C$
has an almost rational cluster picture and is
$C$
has an almost rational cluster picture and is
![]() $y$
-regular, and all proper clusters
$y$
-regular, and all proper clusters
![]() $\mathfrak{s}\in \Sigma _C$
have same rational centre
$\mathfrak{s}\in \Sigma _C$
have same rational centre
![]() $w\in K$
. Let
$w\in K$
. Let
![]() ${\mathfrak{s}}_1\subset \dots \subset{\mathfrak{s}}_n=\mathfrak{R}$
be the proper clusters in
${\mathfrak{s}}_1\subset \dots \subset{\mathfrak{s}}_n=\mathfrak{R}$
be the proper clusters in
![]() $\Sigma _C^{\textrm{rat}}$
. For every
$\Sigma _C^{\textrm{rat}}$
. For every
![]() $j=0,\dots,g-1$
, define
$j=0,\dots,g-1$
, define
and
Then the differentials
form an
![]() $O_K$
-basis of
$O_K$
-basis of
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
.
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
.
Proof. Let
![]() $C^w:y^2=f(x+w)$
be the hyperelliptic curve isomorphic to
$C^w:y^2=f(x+w)$
be the hyperelliptic curve isomorphic to
![]() $C$
through the change of variable
$C$
through the change of variable
![]() $y\mapsto y,$
$y\mapsto y,$
![]() $x\mapsto x+w$
. By Corollary 3.25 and Lemma 4.12, the curve
$x\mapsto x+w$
. By Corollary 3.25 and Lemma 4.12, the curve
![]() $C^w$
is
$C^w$
is
![]() $\Delta _v$
-regular. Since
$\Delta _v$
-regular. Since
![]() $\Sigma _C^{\textrm{rat}}$
consists of the proper clusters in
$\Sigma _C^{\textrm{rat}}$
consists of the proper clusters in
![]() $\Sigma _C^w$
, Lemma 4.3 and [Reference Dokchitser1, Theorem 8.12] implies that
$\Sigma _C^w$
, Lemma 4.3 and [Reference Dokchitser1, Theorem 8.12] implies that
form an
![]() $O_K$
-basis of
$O_K$
-basis of
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
as a lattice in
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
as a lattice in
![]() $H^0(C^w,\Omega ^1_{C^w/K})$
(that is if
$H^0(C^w,\Omega ^1_{C^w/K})$
(that is if
![]() $\mathcal{C}$
is regarded as a model of
$\mathcal{C}$
is regarded as a model of
![]() $C^w$
). Changing variables concludes the proof.
$C^w$
). Changing variables concludes the proof.
Suppose now
![]() $C$
has an almost rational cluster picture and is
$C$
has an almost rational cluster picture and is
![]() $y$
-regular. Let
$y$
-regular. Let
![]() $\Sigma _C^{\textrm{min}}$
be the set of rationally minimal clusters and let
$\Sigma _C^{\textrm{min}}$
be the set of rationally minimal clusters and let
![]() $W=\{w_{\mathfrak{s}}\,\mid \,\mathfrak{s}\in \Sigma _C^{\textrm{min}}\}$
be a corresponding set of rational centres, such that all clusters in
$W=\{w_{\mathfrak{s}}\,\mid \,\mathfrak{s}\in \Sigma _C^{\textrm{min}}\}$
be a corresponding set of rational centres, such that all clusters in
![]() $\Sigma _C^{w_{\mathfrak{s}}}$
are proper. For every proper cluster
$\Sigma _C^{w_{\mathfrak{s}}}$
are proper. For every proper cluster
![]() $\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
, choose a minimal cluster
$\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
, choose a minimal cluster
![]() $\mathfrak{s}\subseteq \mathfrak{t}$
and set
$\mathfrak{s}\subseteq \mathfrak{t}$
and set
![]() $w_{\mathfrak{t}}\;:\!=\;w_{\mathfrak{s}}$
. Consider the regular model
$w_{\mathfrak{t}}\;:\!=\;w_{\mathfrak{s}}$
. Consider the regular model
![]() $\mathcal{C}/O_K$
of
$\mathcal{C}/O_K$
of
![]() $C$
of Theorem 4.18, constructed in Section 5 by glueing the open subschemes
$C$
of Theorem 4.18, constructed in Section 5 by glueing the open subschemes
![]() $\mathring{\mathcal{C}}_\Delta ^{w}$
of
$\mathring{\mathcal{C}}_\Delta ^{w}$
of
![]() $\mathcal{C}_\Delta ^w$
for
$\mathcal{C}_\Delta ^w$
for
![]() $w\in W$
. We want to describe the canonical morphism
$w\in W$
. We want to describe the canonical morphism
![]() $C\rightarrow \mathcal{C}$
. Write
$C\rightarrow \mathcal{C}$
. Write
![]() $W=\{w_1,\dots,w_m\}$
as in Section 5. For any
$W=\{w_1,\dots,w_m\}$
as in Section 5. For any
![]() $h=1,\dots,m$
, let
$h=1,\dots,m$
, let
![]() $\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster and let
$\mathfrak{t}\in \Sigma _C^{w_h}$
be a proper cluster and let
![]() $M$
be a matrix associated to
$M$
be a matrix associated to
![]() $\mathfrak{t}$
. Let
$\mathfrak{t}$
. Let
![]() $C^{w_h}:y^2=f(x+w_h)$
and
$C^{w_h}:y^2=f(x+w_h)$
and
Then, on the affine chart
![]() $X_M$
the projection
$X_M$
the projection
![]() $C\rightarrow \mathcal{C}_\Delta ^{w_h}$
is induced by
$C\rightarrow \mathcal{C}_\Delta ^{w_h}$
is induced by
where
![]() $(X,Y,Z)=(x',y',\pi )\bullet M$
and
$(X,Y,Z)=(x',y',\pi )\bullet M$
and
![]() $(x',y')=(x-w_h,y)$
. In particular it follows that
$(x',y')=(x-w_h,y)$
. In particular it follows that
![]() $(X,Y,Z)=(x-w_h,y,z)\bullet M$
and so
$(X,Y,Z)=(x-w_h,y,z)\bullet M$
and so
 \begin{align*} \begin{pmatrix} x-w_h \\ y \\ \pi \end{pmatrix}= \begin{pmatrix} X^{\tilde{m}_{11}}Y^{\tilde{m}_{21}}Z^{\tilde{m}_{31}}\\ X^{\tilde{m}_{12}}Y^{\tilde{m}_{22}}Z^{\tilde{m}_{32}}\\ X^{\tilde{m}_{13}}Y^{\tilde{m}_{23}}Z^{\tilde{m}_{33}} \end{pmatrix} =\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}\bullet M^{-1}. \end{align*}
\begin{align*} \begin{pmatrix} x-w_h \\ y \\ \pi \end{pmatrix}= \begin{pmatrix} X^{\tilde{m}_{11}}Y^{\tilde{m}_{21}}Z^{\tilde{m}_{31}}\\ X^{\tilde{m}_{12}}Y^{\tilde{m}_{22}}Z^{\tilde{m}_{32}}\\ X^{\tilde{m}_{13}}Y^{\tilde{m}_{23}}Z^{\tilde{m}_{33}} \end{pmatrix} =\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}\bullet M^{-1}. \end{align*}
For a proper cluster
![]() $\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
recall the definitions of
$\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
recall the definitions of
![]() $\Gamma _{\mathfrak{t}}$
and
$\Gamma _{\mathfrak{t}}$
and
![]() $m_{\mathfrak{t}}$
.
$m_{\mathfrak{t}}$
.
Proposition 6.2.
Let
![]() $\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
be a proper cluster. Then
Footnote 5
$\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
be a proper cluster. Then
Footnote 5
for every proper cluster
![]() $\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
,
$\mathfrak{s}\in \Sigma _C^{\textrm{rat}}$
,
![]() $\mathfrak{s}\subseteq \mathfrak{t}$
.
$\mathfrak{s}\subseteq \mathfrak{t}$
.
Proof. Let
![]() $g(x,y)=y^2-f(x)$
. Let
$g(x,y)=y^2-f(x)$
. Let
![]() $W=\{w_1,\dots,w_m\}$
as above. Let
$W=\{w_1,\dots,w_m\}$
as above. Let
![]() $h\in \{1,\dots,m\}$
such that
$h\in \{1,\dots,m\}$
such that
![]() $w_h=w_{\mathfrak{s}}$
. Let
$w_h=w_{\mathfrak{s}}$
. Let
![]() $F=F_{\mathfrak{t}}^{w_h}$
,
$F=F_{\mathfrak{t}}^{w_h}$
,
![]() $V=V_{\mathfrak{t}}^{w_h}$
,
$V=V_{\mathfrak{t}}^{w_h}$
,
![]() $M=M_{V,0}$
and let
$M=M_{V,0}$
and let
![]() $X,Y,Z$
be the transformed variables
$X,Y,Z$
be the transformed variables
![]() $(X,Y,Z)=(x-w_{\mathfrak{s}},y,\pi )\bullet M$
. Define
$(X,Y,Z)=(x-w_{\mathfrak{s}},y,\pi )\bullet M$
. Define
![]() $\mathcal{H}(X,Y,Z)=\pi - X^{\tilde{m}_{13}}Y^{\tilde{m}_{23}}Z^{\tilde{m}_{33}}$
, and
$\mathcal{H}(X,Y,Z)=\pi - X^{\tilde{m}_{13}}Y^{\tilde{m}_{23}}Z^{\tilde{m}_{33}}$
, and
![]() $\mathcal{G}(X,Y,Z)=g((X,Y,Z)\bullet M^{-1})$
. We have
$\mathcal{G}(X,Y,Z)=g((X,Y,Z)\bullet M^{-1})$
. We have
where
![]() $n_Z=m_{\mathfrak{t}}\epsilon _{\mathfrak{t}}$
, since
$n_Z=m_{\mathfrak{t}}\epsilon _{\mathfrak{t}}$
, since
![]() $\textrm{ord}_Z(y^2)=m_{\mathfrak{t}}\epsilon _{\mathfrak{t}}$
for Lemma 5.2. Write
$\textrm{ord}_Z(y^2)=m_{\mathfrak{t}}\epsilon _{\mathfrak{t}}$
for Lemma 5.2. Write
![]() $\mathcal{F}=\mathcal{F}_M^h$
.
$\mathcal{F}=\mathcal{F}_M^h$
.
Note that
![]() $d(x-w_{\mathfrak{s}})=dx$
and
$d(x-w_{\mathfrak{s}})=dx$
and
![]() $(g_{w_{\mathfrak{s}}})_x^{\prime}(x-w_{\mathfrak{s}})=g_x^{\prime}(x)$
, where
$(g_{w_{\mathfrak{s}}})_x^{\prime}(x-w_{\mathfrak{s}})=g_x^{\prime}(x)$
, where
![]() $g_{w_{\mathfrak{s}}}(x,y)=g(x+w_{\mathfrak{s}},y)$
. Then, by [Reference Dokchitser1, 8.7],
$g_{w_{\mathfrak{s}}}(x,y)=g(x+w_{\mathfrak{s}},y)$
. Then, by [Reference Dokchitser1, 8.7],
 \begin{align*} \begin{cases} (x-w_{\mathfrak{s}})g_x^{\prime}=m_{11}X\mathcal{G}_X^{\prime}+m_{12}Y\mathcal{G}_Y^{\prime}+m_{13}Z\mathcal{G}_Z^{\prime}\\ yg_y^{\prime}=m_{21}X\mathcal{G}_X^{\prime}+m_{22}Y\mathcal{G}_Y^{\prime}+m_{23}Z\mathcal{G}_Z^{\prime} \end{cases} \end{align*}
\begin{align*} \begin{cases} (x-w_{\mathfrak{s}})g_x^{\prime}=m_{11}X\mathcal{G}_X^{\prime}+m_{12}Y\mathcal{G}_Y^{\prime}+m_{13}Z\mathcal{G}_Z^{\prime}\\ yg_y^{\prime}=m_{21}X\mathcal{G}_X^{\prime}+m_{22}Y\mathcal{G}_Y^{\prime}+m_{23}Z\mathcal{G}_Z^{\prime} \end{cases} \end{align*}
from which it follows that
We will show later that this quantity is non-zero. Moreover,
Recall that
![]() $X=(x-w_{\mathfrak{s}})^{m_{11}}y^{m_{21}}\pi ^{m_{31}}$
. Then
$X=(x-w_{\mathfrak{s}})^{m_{11}}y^{m_{21}}\pi ^{m_{31}}$
. Then
![]() $\frac{dX}{X}=m_{11}\tfrac{dx}{x-w_{\mathfrak{s}}}+m_{21}\tfrac{dy}{y}$
. Furthermore, as
$\frac{dX}{X}=m_{11}\tfrac{dx}{x-w_{\mathfrak{s}}}+m_{21}\tfrac{dy}{y}$
. Furthermore, as
![]() $0=dg=g_x^{\prime}dx+g_y^{\prime}dy$
in
$0=dg=g_x^{\prime}dx+g_y^{\prime}dy$
in
![]() $\Omega _{C/K}$
, we have
$\Omega _{C/K}$
, we have
 \begin{align*} \frac{dX}{X}=\left (\frac{m_{11}}{x-w_{\mathfrak{s}}}-\frac{m_{21}}{y}\frac{g_x^{\prime}}{g_y^{\prime}}\right ) dx=\frac{dx}{(x-w_{\mathfrak{s}})yg_y^{\prime}}\left ( m_{11}yg_y^{\prime}-m_{21}(x-w_{\mathfrak{s}}) g_x^{\prime}\right ). \end{align*}
\begin{align*} \frac{dX}{X}=\left (\frac{m_{11}}{x-w_{\mathfrak{s}}}-\frac{m_{21}}{y}\frac{g_x^{\prime}}{g_y^{\prime}}\right ) dx=\frac{dx}{(x-w_{\mathfrak{s}})yg_y^{\prime}}\left ( m_{11}yg_y^{\prime}-m_{21}(x-w_{\mathfrak{s}}) g_x^{\prime}\right ). \end{align*}
Therefore
Let
![]() $S=\textrm{Spec}\, O_K$
. Considering
$S=\textrm{Spec}\, O_K$
. Considering
![]() $X^{-1}$
as an independent variable, the scheme
$X^{-1}$
as an independent variable, the scheme
defines a complete intersection in
![]() ${\mathbb{A}}_S^4$
. Furthermore,
${\mathbb{A}}_S^4$
. Furthermore,
![]() $U$
is an open subscheme of
$U$
is an open subscheme of
![]() $\mathcal{C}_\Delta ^{w_h}\cap X_M$
that restricted to
$\mathcal{C}_\Delta ^{w_h}\cap X_M$
that restricted to
![]() ${\mathbb{A}}_S^4\setminus \{T_M^h(X,Y,Z)=0\}$
equals
${\mathbb{A}}_S^4\setminus \{T_M^h(X,Y,Z)=0\}$
equals
![]() $U_M^h$
. In particular,
$U_M^h$
. In particular,
![]() $U$
is integral. From Section 5.5 it follows that
$U$
is integral. From Section 5.5 it follows that
![]() $U_{\mathfrak{t}}=U\cap \{Z=0\}$
is a dense open subset of
$U_{\mathfrak{t}}=U\cap \{Z=0\}$
is a dense open subset of
![]() $ X_{F}$
. Recall that
$ X_{F}$
. Recall that
![]() $ X_{F}$
is an open subscheme of
$ X_{F}$
is an open subscheme of
![]() $\Gamma _{\mathfrak{t}}$
. Hence it suffices to prove the proposition for
$\Gamma _{\mathfrak{t}}$
. Hence it suffices to prove the proposition for
![]() $U_{\mathfrak{t}}$
instead of
$U_{\mathfrak{t}}$
instead of
![]() $\Gamma _{\mathfrak{t}}$
([Reference Liu9, Lemma 9.2.17(a)]). Since
$\Gamma _{\mathfrak{t}}$
([Reference Liu9, Lemma 9.2.17(a)]). Since
![]() $X$
and
$X$
and
![]() $Y$
are units and
$Y$
are units and
![]() $Z$
vanishes to order
$Z$
vanishes to order
![]() $1$
on
$1$
on
![]() $U_{\mathfrak{t}}$
, Lemma 5.2 implies that
$U_{\mathfrak{t}}$
, Lemma 5.2 implies that
Recall that
![]() $U$
is integral and that
$U$
is integral and that
![]() $U_\eta$
is isomorphic to an open subscheme of
$U_\eta$
is isomorphic to an open subscheme of
![]() $C$
. Then
$C$
. Then
![]() $U_\eta$
is smooth. Hence, by [Reference Liu9, Corollary 6.4.14(b)], the sheaf
$U_\eta$
is smooth. Hence, by [Reference Liu9, Corollary 6.4.14(b)], the sheaf
![]() $\omega _{\mathcal{C}/O_K}$
is generated on
$\omega _{\mathcal{C}/O_K}$
is generated on
![]() $U$
by
$U$
by
![]() $\mathcal{E}^{-1}dX$
where
$\mathcal{E}^{-1}dX$
where
 \begin{equation} \mathcal{E}\;:\!=\;\left |\begin{matrix}\mathcal{F}^{\prime}_Y&\mathcal{F}^{\prime}_Z&\mathcal{F}_{X^{-1}}^{\prime}\\ H_Y^{\prime}&H_Z^{\prime}&\mathcal{F}_{X^{-1}}^{\prime}\\ 0&0&X\end{matrix}\right |=-\pi X Y^{-1}Z^{-1}\left ( \tilde{m}_{33}Y\mathcal{F}_Y^{\prime}-\tilde{m}_{23}Z\mathcal{F}_Z^{\prime}\right ), \end{equation}
\begin{equation} \mathcal{E}\;:\!=\;\left |\begin{matrix}\mathcal{F}^{\prime}_Y&\mathcal{F}^{\prime}_Z&\mathcal{F}_{X^{-1}}^{\prime}\\ H_Y^{\prime}&H_Z^{\prime}&\mathcal{F}_{X^{-1}}^{\prime}\\ 0&0&X\end{matrix}\right |=-\pi X Y^{-1}Z^{-1}\left ( \tilde{m}_{33}Y\mathcal{F}_Y^{\prime}-\tilde{m}_{23}Z\mathcal{F}_Z^{\prime}\right ), \end{equation}
if
![]() $\mathcal{E}$
is non-zero. Suppose it is; we are going to prove it later. Thus, as
$\mathcal{E}$
is non-zero. Suppose it is; we are going to prove it later. Thus, as
![]() $\mathcal{F}=0$
on
$\mathcal{F}=0$
on
![]() $U$
, we have
$U$
, we have
 \begin{align*} \textrm{ord}_{U_{\mathfrak{t}}}\frac{dx}{2(x-w_{\mathfrak{s}})y^2}&=\textrm{ord}_{U_{\mathfrak{t}}}\tfrac{dX}{XY^{n_Y}Z^{n_Z}\left ( \tilde{m}_{33}Y\mathcal{F}_Y^{\prime}-\tilde{m}_{23}Z\mathcal{F}_Z^{\prime}\right )}&&\text{from (11)}\\ &=\textrm{ord}_{U_{\mathfrak{t}}}\left (\pi Y^{-n_Y-1}Z^{-n_Z-1}\mathcal{E}^{-1}dX\right )&&\text{from (13)}\\ &=m_{\mathfrak{t}}-n_Z-1=m_{\mathfrak{t}}\left ( -\epsilon _{\mathfrak{t}}+1\right )-1&&\text{from (12).} \end{align*}
\begin{align*} \textrm{ord}_{U_{\mathfrak{t}}}\frac{dx}{2(x-w_{\mathfrak{s}})y^2}&=\textrm{ord}_{U_{\mathfrak{t}}}\tfrac{dX}{XY^{n_Y}Z^{n_Z}\left ( \tilde{m}_{33}Y\mathcal{F}_Y^{\prime}-\tilde{m}_{23}Z\mathcal{F}_Z^{\prime}\right )}&&\text{from (11)}\\ &=\textrm{ord}_{U_{\mathfrak{t}}}\left (\pi Y^{-n_Y-1}Z^{-n_Z-1}\mathcal{E}^{-1}dX\right )&&\text{from (13)}\\ &=m_{\mathfrak{t}}-n_Z-1=m_{\mathfrak{t}}\left ( -\epsilon _{\mathfrak{t}}+1\right )-1&&\text{from (12).} \end{align*}
Then it follows from (12) that
It remains to show that
![]() $\mathcal{E}$
does not equal
$\mathcal{E}$
does not equal
![]() $0$
on
$0$
on
![]() $U$
. Suppose it does. Then from the computations above, it follows that
$U$
. Suppose it does. Then from the computations above, it follows that
![]() $m_{11}y g_y^{\prime}-m_{21}(x-w_{\mathfrak{s}})g_x^{\prime}=0$
in
$m_{11}y g_y^{\prime}-m_{21}(x-w_{\mathfrak{s}})g_x^{\prime}=0$
in
![]() $K(C)$
. Since
$K(C)$
. Since
![]() $m_{21}$
equals either
$m_{21}$
equals either
![]() $1$
or
$1$
or
![]() $2$
by Lemma 5.2, it follows that there exists a non-zero
$2$
by Lemma 5.2, it follows that there exists a non-zero
![]() $c\in K$
, such that
$c\in K$
, such that
(
![]() $c\in K$
from degree analysis). Then
$c\in K$
from degree analysis). Then
![]() $cf(x)=m_{21}(x-w_{\mathfrak{s}})f'(x)$
. Note that
$cf(x)=m_{21}(x-w_{\mathfrak{s}})f'(x)$
. Note that
![]() $m_{21}$
is non-zero as
$m_{21}$
is non-zero as
![]() $\textrm{char}(K)\neq 2$
. But then a contradiction follows since
$\textrm{char}(K)\neq 2$
. But then a contradiction follows since
![]() $f$
is a separable polynomial of degree
$f$
is a separable polynomial of degree
![]() $\geq 3$
.
$\geq 3$
.
In the following two theorems we describe a basis of integral differentials of
![]() $C$
. We use Definitions/Notations 3.1, 3.3, 3.2, 3.8, 3.9, 3.26, 4.6, 4.10 in the statements.
$C$
. We use Definitions/Notations 3.1, 3.3, 3.2, 3.8, 3.9, 3.26, 4.6, 4.10 in the statements.
Theorem 6.3.
Let
![]() $C/K$
be a hyperelliptic curve of genus
$C/K$
be a hyperelliptic curve of genus
![]() $g\geq 1$
defined by the Weierstrass equation
$g\geq 1$
defined by the Weierstrass equation
![]() $y^2=f(x)$
and let
$y^2=f(x)$
and let
![]() $\mathcal{C}/O_K$
be a regular model of
$\mathcal{C}/O_K$
be a regular model of
![]() $C$
. Suppose
$C$
. Suppose
![]() $C$
has an almost rational cluster picture and is
$C$
has an almost rational cluster picture and is
![]() $y$
-regular. For
$y$
-regular. For
![]() $i=0,\dots,g-1$
inductively
$i=0,\dots,g-1$
inductively
-
(i) define
 $e_i\;:\!=\;\displaystyle \max _{\mathfrak{t}\in \Sigma _C^{\textrm{rat}}}\bigg \{\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}$
;
$e_i\;:\!=\;\displaystyle \max _{\mathfrak{t}\in \Sigma _C^{\textrm{rat}}}\bigg \{\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}$
; -
(ii) choose a maximal element
 ${\mathfrak{s}}_i$
of
${\mathfrak{s}}_i$
of
 $\displaystyle \bigg \{\mathfrak{t}\in \Sigma _C^{\textrm{rat}}\mid \,e_i=\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}$
freely.
$\displaystyle \bigg \{\mathfrak{t}\in \Sigma _C^{\textrm{rat}}\mid \,e_i=\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}$
freely.
Then the differentials
 \begin{align*} \mu _i=\pi ^{\lfloor e_i\rfloor }\prod _{j=0}^{i-1}(x-w_{{\mathfrak{s}}_j})\frac{dx}{2y},\qquad i=0,\dots,g-1, \end{align*}
\begin{align*} \mu _i=\pi ^{\lfloor e_i\rfloor }\prod _{j=0}^{i-1}(x-w_{{\mathfrak{s}}_j})\frac{dx}{2y},\qquad i=0,\dots,g-1, \end{align*}
form an
![]() $O_K$
-basis of
$O_K$
-basis of
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
.
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
.
Proof. Since
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
is independent of the choice of regular model, we consider
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
is independent of the choice of regular model, we consider
![]() $\mathcal{C}$
to be the model described in Theorem 4.18 and constructed in Section 5.
$\mathcal{C}$
to be the model described in Theorem 4.18 and constructed in Section 5.
We first show that the differentials
![]() $\mu _i$
are global sections of
$\mu _i$
are global sections of
![]() $\omega _{\mathcal{C}/O_K}$
. It suffices to prove they are regular along all components
$\omega _{\mathcal{C}/O_K}$
. It suffices to prove they are regular along all components
![]() $\Gamma _{\mathfrak{t}}$
, where
$\Gamma _{\mathfrak{t}}$
, where
![]() $\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
proper. Indeed for the construction of
$\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
proper. Indeed for the construction of
![]() $\mathcal{C}$
and the definition of the
$\mathcal{C}$
and the definition of the
![]() $e_i$
’s, the differentials
$e_i$
’s, the differentials
![]() $\mu _i$
are regular along all other components of
$\mu _i$
are regular along all other components of
![]() $\mathcal{C}_s$
by Theorem 6.1. Fix
$\mathcal{C}_s$
by Theorem 6.1. Fix
![]() $i=1,\dots,g-1$
and let
$i=1,\dots,g-1$
and let
![]() $j=0,\dots,i-1$
. Let
$j=0,\dots,i-1$
. Let
![]() $\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
be a proper cluster. If
$\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
be a proper cluster. If
![]() ${\mathfrak{s}}_j\subseteq \mathfrak{t}$
then
${\mathfrak{s}}_j\subseteq \mathfrak{t}$
then
by Proposition 6.2. If
![]() $\mathfrak{t}\subsetneq{\mathfrak{s}}_j$
then
$\mathfrak{t}\subsetneq{\mathfrak{s}}_j$
then
![]() $w_{\mathfrak{t}}$
is a rational centre of
$w_{\mathfrak{t}}$
is a rational centre of
![]() ${\mathfrak{s}}_j$
. Hence
${\mathfrak{s}}_j$
. Hence
Therefore Proposition 6.2 implies
If
![]() ${\mathfrak{s}}_j\nsubseteq \mathfrak{t}$
and
${\mathfrak{s}}_j\nsubseteq \mathfrak{t}$
and
![]() $\mathfrak{t}\nsubseteq{\mathfrak{s}}_j$
then from Lemma 3.18 it follows that
$\mathfrak{t}\nsubseteq{\mathfrak{s}}_j$
then from Lemma 3.18 it follows that
as
![]() $\rho _{\mathfrak{t}}\gt \rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}$
. Thus we have proved that
$\rho _{\mathfrak{t}}\gt \rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}$
. Thus we have proved that
Hence it follows from Proposition 6.2 that
 \begin{align*} \textrm{ord}_{\Gamma _{\mathfrak{t}}}\mu _i\geq m_{\mathfrak{t}}\bigg (\lfloor e_i\rfloor +\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}-\frac{\epsilon _{\mathfrak{t}}}{2}+\rho _t+1\bigg )-1. \end{align*}
\begin{align*} \textrm{ord}_{\Gamma _{\mathfrak{t}}}\mu _i\geq m_{\mathfrak{t}}\bigg (\lfloor e_i\rfloor +\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}-\frac{\epsilon _{\mathfrak{t}}}{2}+\rho _t+1\bigg )-1. \end{align*}
But
 \begin{align*} \lfloor e_i\rfloor \geq \bigg \lfloor \frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \rfloor \gt \frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}-1, \end{align*}
\begin{align*} \lfloor e_i\rfloor \geq \bigg \lfloor \frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \rfloor \gt \frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}-1, \end{align*}
then
![]() $\textrm{ord}_{\Gamma _{\mathfrak{t}}}\mu _i\gt -1$
, that implies
$\textrm{ord}_{\Gamma _{\mathfrak{t}}}\mu _i\gt -1$
, that implies
![]() $\textrm{ord}_{\Gamma _{\mathfrak{t}}}\mu _i\geq 0$
, as required.
$\textrm{ord}_{\Gamma _{\mathfrak{t}}}\mu _i\geq 0$
, as required.
Now we need to show that the differentials
![]() $\mu _i$
span
$\mu _i$
span
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
, that is the lattice they span is saturated in the global sections of
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
, that is the lattice they span is saturated in the global sections of
![]() $\omega _{\mathcal{C}/O_K}$
. Suppose not. Then there exist
$\omega _{\mathcal{C}/O_K}$
. Suppose not. Then there exist
![]() $I\subseteq \{0,\dots,g-1\}$
and
$I\subseteq \{0,\dots,g-1\}$
and
![]() $u_i\in O_K^\times$
for
$u_i\in O_K^\times$
for
![]() $i\in I$
such that the differential
$i\in I$
such that the differential
![]() $\frac{1}{\pi }\sum _{i\in I}u_i\mu _i$
is regular along
$\frac{1}{\pi }\sum _{i\in I}u_i\mu _i$
is regular along
![]() $\Gamma _{\mathfrak{t}}$
, for every proper cluster
$\Gamma _{\mathfrak{t}}$
, for every proper cluster
![]() $\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
. First we want to show that for any
$\mathfrak{t}\in \Sigma _C^{\textrm{rat}}$
. First we want to show that for any
![]() $i_1,i_2=0,\dots,g-1$
with
$i_1,i_2=0,\dots,g-1$
with
![]() $i_1\lt i_2$
, one has
$i_1\lt i_2$
, one has
![]() ${\mathfrak{s}}_{i_2}\not \subset{\mathfrak{s}}_{i_1}$
. Suppose by contradiction that
${\mathfrak{s}}_{i_2}\not \subset{\mathfrak{s}}_{i_1}$
. Suppose by contradiction that
![]() ${\mathfrak{s}}_{i_2}\subsetneq{\mathfrak{s}}_{i_1}$
. Then
${\mathfrak{s}}_{i_2}\subsetneq{\mathfrak{s}}_{i_1}$
. Then
 \begin{align*} e_{i_2}&\geq \frac{\epsilon _{{\mathfrak{s}}_{i_1}}}{2}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=0}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_1}}= e_{i_1}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=i_1+1}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_1}}\geq e_{i_1}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=i_1+1}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_2}}\\ &\geq \frac{\epsilon _{{\mathfrak{s}}_{i_2}}}{2}-\rho _{{\mathfrak{s}}_{i_2}}-\sum _{j=0}^{i_1-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_2}}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=i_1+1}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_2}}=\frac{\epsilon _{{\mathfrak{s}}_{i_2}}}{2}-\sum _{j=0}^{i_2}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_2}}=e_{i_2}. \end{align*}
\begin{align*} e_{i_2}&\geq \frac{\epsilon _{{\mathfrak{s}}_{i_1}}}{2}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=0}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_1}}= e_{i_1}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=i_1+1}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_1}}\geq e_{i_1}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=i_1+1}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_2}}\\ &\geq \frac{\epsilon _{{\mathfrak{s}}_{i_2}}}{2}-\rho _{{\mathfrak{s}}_{i_2}}-\sum _{j=0}^{i_1-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_2}}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=i_1+1}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_2}}=\frac{\epsilon _{{\mathfrak{s}}_{i_2}}}{2}-\sum _{j=0}^{i_2}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_2}}=e_{i_2}. \end{align*}
Therefore
 \begin{align*} \max _{\mathfrak{t}\in \Sigma _C^{\textrm{rat}}}\bigg \{\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}=e_{i_2}=\frac{\epsilon _{{\mathfrak{s}}_{i_1}}}{2}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=0}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_1}}, \end{align*}
\begin{align*} \max _{\mathfrak{t}\in \Sigma _C^{\textrm{rat}}}\bigg \{\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}=e_{i_2}=\frac{\epsilon _{{\mathfrak{s}}_{i_1}}}{2}-\rho _{{\mathfrak{s}}_{i_1}}-\sum _{j=0}^{i_2-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_1}}, \end{align*}
and this means that
![]() ${\mathfrak{s}}_{i_1}$
is a possible choice for the
${\mathfrak{s}}_{i_1}$
is a possible choice for the
![]() $i_2$
th cluster
$i_2$
th cluster
![]() ${\mathfrak{s}}_{i_2}$
. But
${\mathfrak{s}}_{i_2}$
. But
![]() ${\mathfrak{s}}_{i_2}\subsetneq{\mathfrak{s}}_{i_1}$
, so the
${\mathfrak{s}}_{i_2}\subsetneq{\mathfrak{s}}_{i_1}$
, so the
![]() $i_2$
th cluster should have been
$i_2$
th cluster should have been
![]() ${\mathfrak{s}}_{i_1}$
, a contradiction.
${\mathfrak{s}}_{i_1}$
, a contradiction.
Let
![]() $I_0\subseteq I$
be the set of indices
$I_0\subseteq I$
be the set of indices
![]() $i$
such that
$i$
such that
![]() $\gamma _i\;:\!=\;e_i-\lfloor e_i\rfloor$
is maximal. Let
$\gamma _i\;:\!=\;e_i-\lfloor e_i\rfloor$
is maximal. Let
![]() $i_0=\min I_0$
and let
$i_0=\min I_0$
and let
![]() $\Gamma _0=\Gamma _{{\mathfrak{s}}_{i_0}}$
. Since
$\Gamma _0=\Gamma _{{\mathfrak{s}}_{i_0}}$
. Since
![]() ${\mathfrak{s}}_{i_0}\not \subset{\mathfrak{s}}_j$
, for all
${\mathfrak{s}}_{i_0}\not \subset{\mathfrak{s}}_j$
, for all
![]() $j=0,\dots,i_0-1$
, from (14) it follows that
$j=0,\dots,i_0-1$
, from (14) it follows that
 \begin{align*} m\;:\!=\;\textrm{ord}_{\Gamma _0}\frac{1}{\pi }\mu _{i_0}&=-m_{{\mathfrak{s}}_{i_0}}\gamma _{i_0}+m_{{\mathfrak{s}}_{i_0}}\bigg (e_{i_0}-\frac{\epsilon _{{\mathfrak{s}}_{i_0}}}{2}+\rho _{{\mathfrak{s}}_{i_0}}+\sum _{j=0}^{i_0-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}\bigg )-1\\ &=-m_{{\mathfrak{s}}_{i_0}}\gamma _{i_0}-1\lt 0. \end{align*}
\begin{align*} m\;:\!=\;\textrm{ord}_{\Gamma _0}\frac{1}{\pi }\mu _{i_0}&=-m_{{\mathfrak{s}}_{i_0}}\gamma _{i_0}+m_{{\mathfrak{s}}_{i_0}}\bigg (e_{i_0}-\frac{\epsilon _{{\mathfrak{s}}_{i_0}}}{2}+\rho _{{\mathfrak{s}}_{i_0}}+\sum _{j=0}^{i_0-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}\bigg )-1\\ &=-m_{{\mathfrak{s}}_{i_0}}\gamma _{i_0}-1\lt 0. \end{align*}
Furthermore,
 \begin{align*} \textrm{ord}_{\Gamma _0}\frac{1}{\pi }\mu _{i}&\geq -m_{{\mathfrak{s}}_{i_0}}\gamma _{i}+m_{{\mathfrak{s}}_{i_0}}\bigg (e_{i}-\frac{\epsilon _{{\mathfrak{s}}_{i_0}}}{2}+\rho _{{\mathfrak{s}}_{i_0}}+\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}\bigg )-1\\ &\geq -m_{{\mathfrak{s}}_{i_0}}\gamma _{i}-1\geq -m_{{\mathfrak{s}}_{i_0}}\gamma _{i_0}-1=m, \end{align*}
\begin{align*} \textrm{ord}_{\Gamma _0}\frac{1}{\pi }\mu _{i}&\geq -m_{{\mathfrak{s}}_{i_0}}\gamma _{i}+m_{{\mathfrak{s}}_{i_0}}\bigg (e_{i}-\frac{\epsilon _{{\mathfrak{s}}_{i_0}}}{2}+\rho _{{\mathfrak{s}}_{i_0}}+\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}\bigg )-1\\ &\geq -m_{{\mathfrak{s}}_{i_0}}\gamma _{i}-1\geq -m_{{\mathfrak{s}}_{i_0}}\gamma _{i_0}-1=m, \end{align*}
for all
![]() $i\in I$
. Let
$i\in I$
. Let
![]() $J\;:\!=\;\{i\in I\mid \textrm{ord}_{\Gamma _0}\frac{1}{\pi }\mu _i=m\}$
. Then
$J\;:\!=\;\{i\in I\mid \textrm{ord}_{\Gamma _0}\frac{1}{\pi }\mu _i=m\}$
. Then
![]() $J\neq \varnothing$
since
$J\neq \varnothing$
since
![]() $i_0\in J$
. The order of the differential
$i_0\in J$
. The order of the differential
![]() $\frac{1}{\pi }\sum _{i\in J} u_i\mu _i$
along
$\frac{1}{\pi }\sum _{i\in J} u_i\mu _i$
along
![]() $\Gamma _0$
must be
$\Gamma _0$
must be
![]() $\gt m$
. Let
$\gt m$
. Let
![]() $i\in I$
. From the computations above
$i\in I$
. From the computations above
![]() $i\in J$
if and only if
$i\in J$
if and only if
-
(i)
 $\textrm{ord}_{\Gamma _0}(x-w_{{\mathfrak{s}}_j})=m_{{\mathfrak{s}}_{i_0}}\rho _{{\mathfrak{s}}_{i_0}\wedge{\mathfrak{s}}_j}$
for all
$\textrm{ord}_{\Gamma _0}(x-w_{{\mathfrak{s}}_j})=m_{{\mathfrak{s}}_{i_0}}\rho _{{\mathfrak{s}}_{i_0}\wedge{\mathfrak{s}}_j}$
for all
 $j=0,\dots,i-1$
. Equivalently, if
$j=0,\dots,i-1$
. Equivalently, if
 ${\mathfrak{s}}_j\supsetneq{\mathfrak{s}}_{i_0}$
for some
${\mathfrak{s}}_j\supsetneq{\mathfrak{s}}_{i_0}$
for some
 $j\lt i$
, then
$j\lt i$
, then
 $v(w_{{\mathfrak{s}}_{i_0}}-w_{{\mathfrak{s}}_j})=\rho _{{\mathfrak{s}}_{i_0}\wedge{\mathfrak{s}}_j}$
.
$v(w_{{\mathfrak{s}}_{i_0}}-w_{{\mathfrak{s}}_j})=\rho _{{\mathfrak{s}}_{i_0}\wedge{\mathfrak{s}}_j}$
. -
(ii)
 $e_i=\frac{\epsilon _{{\mathfrak{s}}_{i_0}}}{2}-\rho _{{\mathfrak{s}}_{i_0}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}$
. In particular, if
$e_i=\frac{\epsilon _{{\mathfrak{s}}_{i_0}}}{2}-\rho _{{\mathfrak{s}}_{i_0}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}$
. In particular, if
 ${\mathfrak{s}}_i\subseteq{\mathfrak{s}}_{i_0}$
, then
${\mathfrak{s}}_i\subseteq{\mathfrak{s}}_{i_0}$
, then
 ${\mathfrak{s}}_i={\mathfrak{s}}_{i_0}$
.
${\mathfrak{s}}_i={\mathfrak{s}}_{i_0}$
. -
(iii)
 $\gamma _i=\gamma _{i_0}$
. Equivalently,
$\gamma _i=\gamma _{i_0}$
. Equivalently,
 $i\in I_0$
.
$i\in I_0$
.
Therefore
![]() $J\subseteq I_0$
,
$J\subseteq I_0$
,
![]() $i_0=\min J$
and
$i_0=\min J$
and
 \begin{align*} \lfloor e_i\rfloor -\lfloor e_{i_0}\rfloor =e_i-\gamma _i-e_{i_0}+\gamma _{i_0}=e_i-e_{i_0}=-\sum _{j=i_0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}, \end{align*}
\begin{align*} \lfloor e_i\rfloor -\lfloor e_{i_0}\rfloor =e_i-\gamma _i-e_{i_0}+\gamma _{i_0}=e_i-e_{i_0}=-\sum _{j=i_0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}, \end{align*}
for all
![]() $i\in J$
. Hence
$i\in J$
. Hence
 \begin{align*} \frac{1}{\pi }\sum _{i\in{J}}u_i\mu _i=\frac{1}{\pi }\mu _{i_0}\bigg (\sum _{i\in{J}}\frac{u_i}{\pi ^{\sum _{j=i_0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}}}\prod _{j=i_0}^{i-1}(x-w_{{\mathfrak{s}}_j})\bigg ), \end{align*}
\begin{align*} \frac{1}{\pi }\sum _{i\in{J}}u_i\mu _i=\frac{1}{\pi }\mu _{i_0}\bigg (\sum _{i\in{J}}\frac{u_i}{\pi ^{\sum _{j=i_0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}}}\prod _{j=i_0}^{i-1}(x-w_{{\mathfrak{s}}_j})\bigg ), \end{align*}
and since
![]() $\textrm{ord}_{\Gamma _0}\frac{1}{\pi }\mu _{i_0}=m\lt 0$
we must have
$\textrm{ord}_{\Gamma _0}\frac{1}{\pi }\mu _{i_0}=m\lt 0$
we must have
 \begin{equation} \textrm{ord}_{\Gamma _0}\bigg (\sum _{i\in{J}}\frac{u_i}{\pi ^{\sum _{j=i_0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}}}\prod _{j=i_0}^{i-1}(x-w_{{\mathfrak{s}}_j})\bigg )\gt 0. \end{equation}
\begin{equation} \textrm{ord}_{\Gamma _0}\bigg (\sum _{i\in{J}}\frac{u_i}{\pi ^{\sum _{j=i_0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}}}\prod _{j=i_0}^{i-1}(x-w_{{\mathfrak{s}}_j})\bigg )\gt 0. \end{equation}
For any
![]() $j\lt i\in J$
, with
$j\lt i\in J$
, with
![]() $i_0\leq j$
we have
$i_0\leq j$
we have
![]() ${\mathfrak{s}}_j\not \subset{\mathfrak{s}}_{i_0}$
. Therefore either
${\mathfrak{s}}_j\not \subset{\mathfrak{s}}_{i_0}$
. Therefore either
![]() ${\mathfrak{s}}_j={\mathfrak{s}}_{i_0}$
or
${\mathfrak{s}}_j={\mathfrak{s}}_{i_0}$
or
![]() ${\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}\supsetneq{\mathfrak{s}}_{i_0}$
. In the latter case,
${\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}\supsetneq{\mathfrak{s}}_{i_0}$
. In the latter case,
It follows from (15) that
where
![]() $J_i=\{j\in I\mid i_0\leq j\lt i \mbox{ and }{\mathfrak{s}}_j\neq{\mathfrak{s}}_{i_0}\}$
,
$J_i=\{j\in I\mid i_0\leq j\lt i \mbox{ and }{\mathfrak{s}}_j\neq{\mathfrak{s}}_{i_0}\}$
,
![]() $v_i=u_i\prod _{j\in J_i}\frac{w_{{\mathfrak{s}}_{i_0}}-w_{{\mathfrak{s}}_{j}}}{\pi ^{\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}}}\in O_K^\times$
, and
$v_i=u_i\prod _{j\in J_i}\frac{w_{{\mathfrak{s}}_{i_0}}-w_{{\mathfrak{s}}_{j}}}{\pi ^{\rho _{{\mathfrak{s}}_j\wedge{\mathfrak{s}}_{i_0}}}}\in O_K^\times$
, and
![]() $\beta _i=|\{i_0,\dots,i-1\}\setminus J_i|$
.
$\beta _i=|\{i_0,\dots,i-1\}\setminus J_i|$
.
To find a contradiction, we will use the explicit description of a dense open affine subset of
![]() $\Gamma _0$
. Let
$\Gamma _0$
. Let
![]() $W=\{w_1,\dots,w_m\}$
be the set of rational centres of the rationally minimal clusters for
$W=\{w_1,\dots,w_m\}$
be the set of rational centres of the rationally minimal clusters for
![]() $C$
fixed at the beginning of the section. Let
$C$
fixed at the beginning of the section. Let
![]() $w_h\in W$
such that
$w_h\in W$
such that
![]() $w_h=w_{{\mathfrak{s}}_{i_0}}$
, and let
$w_h=w_{{\mathfrak{s}}_{i_0}}$
, and let
![]() $L=L_{{\mathfrak{s}}_{i_0}}^{w_h}$
,
$L=L_{{\mathfrak{s}}_{i_0}}^{w_h}$
,
![]() $M=M_{L,0}$
, and consider
$M=M_{L,0}$
, and consider
dense open subscheme of
![]() $\Gamma _{\mathfrak{t}}$
. From Lemma 5.2,
$\Gamma _{\mathfrak{t}}$
. From Lemma 5.2,
which is a unit since the polynomial
![]() $\mathcal{F}_M^h(X,Y,Z)$
in
$\mathcal{F}_M^h(X,Y,Z)$
in
![]() $\{Z=0\}$
is of the form
$\{Z=0\}$
is of the form
![]() $Y^2-G(X)$
or
$Y^2-G(X)$
or
![]() $Y-G(X)$
for some non-constant
$Y-G(X)$
for some non-constant
![]() $G(X)\in K[X]$
(for more details see Lemma 5.17). This gives a contradiction and concludes the proof.
$G(X)\in K[X]$
(for more details see Lemma 5.17). This gives a contradiction and concludes the proof.
Assume now
![]() $C_{K^{nr}}$
has an almost rational cluster picture and is
$C_{K^{nr}}$
has an almost rational cluster picture and is
![]() $y$
-regular as in Theorem 4.23. Since
$y$
-regular as in Theorem 4.23. Since
![]() $|\Sigma _C|$
is finite, there exists a finite unramified extension
$|\Sigma _C|$
is finite, there exists a finite unramified extension
![]() $F/K$
such that
$F/K$
such that
![]() $C_F$
has an almost rational cluster picture and is
$C_F$
has an almost rational cluster picture and is
![]() $y$
-regular. Denote by
$y$
-regular. Denote by
![]() $O_F$
the ring of integers of
$O_F$
the ring of integers of
![]() $F$
. Let
$F$
. Let
![]() $\Sigma _F=\Sigma _{C_F}^{\textrm{rat}}$
. Fix a rational centre
$\Sigma _F=\Sigma _{C_F}^{\textrm{rat}}$
. Fix a rational centre
![]() $w_{\mathfrak{s}}\in F$
for every rationally minimal cluster
$w_{\mathfrak{s}}\in F$
for every rationally minimal cluster
![]() $\mathfrak{s}\in \Sigma _F$
. For all non-minimal clusters
$\mathfrak{s}\in \Sigma _F$
. For all non-minimal clusters
![]() $\mathfrak{t}\in \Sigma _F$
choose a rational centre
$\mathfrak{t}\in \Sigma _F$
choose a rational centre
![]() $w_{\mathfrak{t}}=w_{\mathfrak{s}}$
for some rationally minimal cluster
$w_{\mathfrak{t}}=w_{\mathfrak{s}}$
for some rationally minimal cluster
![]() $\mathfrak{s}\subseteq \mathfrak{t}$
. In this setting the next theorem gives a basis of integral differentials of
$\mathfrak{s}\subseteq \mathfrak{t}$
. In this setting the next theorem gives a basis of integral differentials of
![]() $C$
.
$C$
.
Theorem 6.4.
Let
![]() $C/K$
be a hyperelliptic curve of genus
$C/K$
be a hyperelliptic curve of genus
![]() $g\geq 1$
defined by the Weierstrass equation
$g\geq 1$
defined by the Weierstrass equation
![]() $y^2=f(x)$
and let
$y^2=f(x)$
and let
![]() $\mathcal{C}/O_K$
be a regular model of
$\mathcal{C}/O_K$
be a regular model of
![]() $C$
. Suppose there exists a finite unramified extension
$C$
. Suppose there exists a finite unramified extension
![]() $F/K$
such that
$F/K$
such that
![]() $C_F$
has an almost rational cluster picture and is
$C_F$
has an almost rational cluster picture and is
![]() $y$
-regular. For
$y$
-regular. For
![]() $i=0,\dots,g-1$
inductively
$i=0,\dots,g-1$
inductively
-
(i) define
 $e_i\;:\!=\;\displaystyle \max _{\mathfrak{t}\in \Sigma _F}\bigg \{\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}$
;
$e_i\;:\!=\;\displaystyle \max _{\mathfrak{t}\in \Sigma _F}\bigg \{\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}$
; -
(ii) choose a maximal element
 ${\mathfrak{s}}_i$
of
${\mathfrak{s}}_i$
of
 $\displaystyle \bigg \{\mathfrak{t}\in \Sigma _F\mid \,e_i=\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}$
freely.
$\displaystyle \bigg \{\mathfrak{t}\in \Sigma _F\mid \,e_i=\frac{\epsilon _{\mathfrak{t}}}{2}-\rho _{\mathfrak{t}}-\sum _{j=0}^{i-1}\rho _{{\mathfrak{s}}_j\wedge \mathfrak{t}}\bigg \}$
freely.
Then the differentials
 \begin{align*} \mu _i=\pi ^{\lfloor e_i\rfloor }\cdot \textrm{Tr}_{F/K}\bigg (\beta \prod _{j=0}^{i-1}(x-w_{{\mathfrak{s}}_j})\bigg )\frac{dx}{2y},\qquad i=0,\dots,g-1, \end{align*}
\begin{align*} \mu _i=\pi ^{\lfloor e_i\rfloor }\cdot \textrm{Tr}_{F/K}\bigg (\beta \prod _{j=0}^{i-1}(x-w_{{\mathfrak{s}}_j})\bigg )\frac{dx}{2y},\qquad i=0,\dots,g-1, \end{align*}
form an
![]() $O_K$
-basis of
$O_K$
-basis of
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
.
$H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})$
.
Proof. First note that without loss of generality we can suppose
![]() $F/K$
Galois. Moreover, since
$F/K$
Galois. Moreover, since
![]() $F/K$
is unramified,
$F/K$
is unramified,
![]() $\textrm{Gal}(F/K)\simeq \textrm{Gal}(\mathfrak{f}/k)$
, where
$\textrm{Gal}(F/K)\simeq \textrm{Gal}(\mathfrak{f}/k)$
, where
![]() $\mathfrak{f}$
is the residue field of
$\mathfrak{f}$
is the residue field of
![]() $F$
, and so the existence of
$F$
, and so the existence of
![]() $\beta$
is guaranteed by the surjectivity of
$\beta$
is guaranteed by the surjectivity of
![]() $\textrm{Tr}_{\mathfrak{f}/k}$
. Let
$\textrm{Tr}_{\mathfrak{f}/k}$
. Let
![]() $\mathcal{C}$
be the minimal regular model of
$\mathcal{C}$
be the minimal regular model of
![]() $C$
over
$C$
over
![]() $O_K$
. By [Reference Liu9, Proposition 10.1.17], the base extended scheme
$O_K$
. By [Reference Liu9, Proposition 10.1.17], the base extended scheme
![]() $\mathcal{C}_{O_F}$
is the minimal regular model of
$\mathcal{C}_{O_F}$
is the minimal regular model of
![]() $C_F$
over
$C_F$
over
![]() $O_F$
. Let
$O_F$
. Let
![]() $\mu _0^F,\dots,\mu _{g-1}^F$
be the basis of integral differentials of
$\mu _0^F,\dots,\mu _{g-1}^F$
be the basis of integral differentials of
![]() $C_F$
given by Theorem 6.3.
$C_F$
given by Theorem 6.3.
Suppose
![]() $\mu _0^{\prime},\dots,\mu _{g-1}^{\prime}$
is a basis of integral differentials of
$\mu _0^{\prime},\dots,\mu _{g-1}^{\prime}$
is a basis of integral differentials of
![]() $C_F$
that, for any
$C_F$
that, for any
![]() $\sigma \in \textrm{Gal}(F/K)$
and any
$\sigma \in \textrm{Gal}(F/K)$
and any
![]() $j=0,\dots,g-1$
, satisfies
$j=0,\dots,g-1$
, satisfies
for some
![]() $\lambda _{ij}\in O_F$
(depending on
$\lambda _{ij}\in O_F$
(depending on
![]() $\sigma$
). Note that
$\sigma$
). Note that
![]() $\mu _0^F,\dots,\mu _{g-1}^F$
is in fact such a basis. We want to prove that, for any
$\mu _0^F,\dots,\mu _{g-1}^F$
is in fact such a basis. We want to prove that, for any
![]() $j=0,\dots,g-1$
, the differentials
$j=0,\dots,g-1$
, the differentials
still form a basis of
![]() $H^0(\mathcal{C}_F,\omega _{\mathcal{C}_F/O_F})$
satisfying condition (16). From equation (16) it follows that
$H^0(\mathcal{C}_F,\omega _{\mathcal{C}_F/O_F})$
satisfying condition (16). From equation (16) it follows that
for some
![]() $\lambda _{ij}^{\prime}\in O_F$
. Since
$\lambda _{ij}^{\prime}\in O_F$
. Since
![]() $\textrm{Tr}_{F/K}(\beta )\in O_K^\times$
, the differentials in (17) form a basis of
$\textrm{Tr}_{F/K}(\beta )\in O_K^\times$
, the differentials in (17) form a basis of
![]() $H^0(\mathcal{C}_F,\omega _{\mathcal{C}_F/O_F})$
satisfying condition (16).
$H^0(\mathcal{C}_F,\omega _{\mathcal{C}_F/O_F})$
satisfying condition (16).
Since
![]() $\mu _0^F,\dots,\mu _{g-1}^F$
satisfies (16), by induction it follows that
$\mu _0^F,\dots,\mu _{g-1}^F$
satisfies (16), by induction it follows that
is a basis of
![]() $H^0(\mathcal{C}_F,\omega _{\mathcal{C}_F/O_F})$
. Proposition B.2 concludes the proof.
$H^0(\mathcal{C}_F,\omega _{\mathcal{C}_F/O_F})$
. Proposition B.2 concludes the proof.
We conclude this section with an application of Theorem 6.3.
Example 6.5.
Let
![]() $p$
be a prime number and let
$p$
be a prime number and let
![]() $a\in \mathbb{Z}_p$
,
$a\in \mathbb{Z}_p$
,
![]() $b\in \mathbb{Z}_p^\times$
such that the polynomial
$b\in \mathbb{Z}_p^\times$
such that the polynomial
![]() $x^2+ax+b$
is not a square modulo
$x^2+ax+b$
is not a square modulo
![]() $p$
. Let
$p$
. Let
![]() $C$
be the hyperelliptic curve over
$C$
be the hyperelliptic curve over
![]() $\mathbb{Q}_p$
of genus
$\mathbb{Q}_p$
of genus
![]() $4$
described by the equation
$4$
described by the equation
![]() $y^2=f(x)$
, where
$y^2=f(x)$
, where
![]() $f(x)=(x^6+ap^4x^3+bp^8)((x-p)^3-p^{11})$
. We have already shown in Examples 3.32 and 4.25 that
$f(x)=(x^6+ap^4x^3+bp^8)((x-p)^3-p^{11})$
. We have already shown in Examples 3.32 and 4.25 that
![]() $C$
satisfies the hypothesis of Theorem 6.3 and has rational cluster picture
$C$
satisfies the hypothesis of Theorem 6.3 and has rational cluster picture

We choose rational centres for the minimal clusters
![]() $\mathfrak{t}_3$
and
$\mathfrak{t}_3$
and
![]() $\mathfrak{t}_4$
:
$\mathfrak{t}_4$
:
![]() $w_{\mathfrak{t}_3}=0$
and
$w_{\mathfrak{t}_3}=0$
and
![]() $w_{\mathfrak{t}_4}=p$
. Since
$w_{\mathfrak{t}_4}=p$
. Since
![]() $\mathfrak{R}=\mathfrak{t}_3\wedge \mathfrak{t}_4$
, we can set either
$\mathfrak{R}=\mathfrak{t}_3\wedge \mathfrak{t}_4$
, we can set either
![]() $w_{\mathfrak{R}}=w_{\mathfrak{t}_3}$
or
$w_{\mathfrak{R}}=w_{\mathfrak{t}_3}$
or
![]() $w_{\mathfrak{R}}=w_{\mathfrak{t}_4}$
. Let us fix
$w_{\mathfrak{R}}=w_{\mathfrak{t}_4}$
. Let us fix
![]() $w_{\mathfrak{R}}=w_{\mathfrak{t}_3}=0$
. Then to choose
$w_{\mathfrak{R}}=w_{\mathfrak{t}_3}=0$
. Then to choose
![]() ${\mathfrak{s}}_0,{\mathfrak{s}}_1,{\mathfrak{s}}_2,{\mathfrak{s}}_3$
as in Theorem 6.3 we draw the following table:
${\mathfrak{s}}_0,{\mathfrak{s}}_1,{\mathfrak{s}}_2,{\mathfrak{s}}_3$
as in Theorem 6.3 we draw the following table:

The numbers in red indicate that
![]() ${\mathfrak{s}}_0=\mathfrak{t}_4$
,
${\mathfrak{s}}_0=\mathfrak{t}_4$
,
![]() ${\mathfrak{s}}_1={\mathfrak{s}}_2=\mathfrak{t}_3$
and
${\mathfrak{s}}_1={\mathfrak{s}}_2=\mathfrak{t}_3$
and
![]() ${\mathfrak{s}}_3=\mathfrak{R}$
. Thus the differentials
${\mathfrak{s}}_3=\mathfrak{R}$
. Thus the differentials
form a
![]() $\mathbb{Z}_p$
-basis of
$\mathbb{Z}_p$
-basis of
![]() $H^0(\mathcal{C},\omega _{\mathcal{C}/\mathbb{Z}_p})$
, for any regular model
$H^0(\mathcal{C},\omega _{\mathcal{C}/\mathbb{Z}_p})$
, for any regular model
![]() $\mathcal{C}/\mathbb{Z}_p$
of
$\mathcal{C}/\mathbb{Z}_p$
of
![]() $C$
.
$C$
.
Acknowledgements
The author would like to thank his supervisor Tim Dokchitser for the very useful conversations, corrections and general advice.
Appendix A: Rational centres over tame extensions
Let
![]() $C/K$
be a hyperelliptic curve given by
$C/K$
be a hyperelliptic curve given by
![]() $y^2=f(x)$
.
$y^2=f(x)$
.
Lemma A.1.
Let
![]() $L/K$
be a field extension. Consider the base extended curve
$L/K$
be a field extension. Consider the base extended curve
![]() $C_L/L$
and its associated cluster picture
$C_L/L$
and its associated cluster picture
![]() $\Sigma _{C_L}$
. Let
$\Sigma _{C_L}$
. Let
![]() $\mathfrak{s}\in \Sigma _{C_L}$
be a proper cluster
$\mathfrak{s}\in \Sigma _{C_L}$
be a proper cluster
![]() $G_{\mathfrak{s}}=\textrm{Stab}_{G_K}(\mathfrak{s})$
, and
$G_{\mathfrak{s}}=\textrm{Stab}_{G_K}(\mathfrak{s})$
, and
![]() $K_{\mathfrak{s}}=\left ( K^{\textrm{s}}\right )^{G_{\mathfrak{s}}}$
. If
$K_{\mathfrak{s}}=\left ( K^{\textrm{s}}\right )^{G_{\mathfrak{s}}}$
. If
![]() $L/L\cap K_{\mathfrak{s}}$
is tamely ramified, then
$L/L\cap K_{\mathfrak{s}}$
is tamely ramified, then
![]() $\mathfrak{s}$
has a rational centre
$\mathfrak{s}$
has a rational centre
![]() $w_{\mathfrak{s}}\in L\cap K_{\mathfrak{s}}$
.
$w_{\mathfrak{s}}\in L\cap K_{\mathfrak{s}}$
.
Proof. Let
![]() $F_{\mathfrak{s}}=L\cap K_{\mathfrak{s}}$
. Let
$F_{\mathfrak{s}}=L\cap K_{\mathfrak{s}}$
. Let
![]() $w_{\mathfrak{s}}\in L$
be a rational centre of
$w_{\mathfrak{s}}\in L$
be a rational centre of
![]() $\mathfrak{s}$
and let
$\mathfrak{s}$
and let
![]() $\rho _{\mathfrak{s}}=\max _{w\in L}\min _{r\in \mathfrak{s}}v(r-w)$
be its radius. Let
$\rho _{\mathfrak{s}}=\max _{w\in L}\min _{r\in \mathfrak{s}}v(r-w)$
be its radius. Let
![]() $\mathcal{D}=\{x\in K^{\textrm{s}}\mid v(x-w_{\mathfrak{s}})\geq \rho _{\mathfrak{s}}\}$
and define
$\mathcal{D}=\{x\in K^{\textrm{s}}\mid v(x-w_{\mathfrak{s}})\geq \rho _{\mathfrak{s}}\}$
and define
![]() $G=\textrm{Stab}_{G_K}(\mathcal{D})$
. Since
$G=\textrm{Stab}_{G_K}(\mathcal{D})$
. Since
![]() $\mathfrak{s}\subseteq \mathcal{D}$
we have
$\mathfrak{s}\subseteq \mathcal{D}$
we have
![]() $G_{\mathfrak{s}}\subseteq G$
. Furthermore,
$G_{\mathfrak{s}}\subseteq G$
. Furthermore,
![]() $\textrm{Gal}(K^{\textrm{s}}/L)\subseteq G$
. Then
$\textrm{Gal}(K^{\textrm{s}}/L)\subseteq G$
. Then
![]() $\textrm{Gal}(K^{\textrm{s}}/F_{\mathfrak{s}})\subseteq G$
. Since
$\textrm{Gal}(K^{\textrm{s}}/F_{\mathfrak{s}})\subseteq G$
. Since
![]() $w_{\mathfrak{s}}\in \mathcal{D}$
, for
$w_{\mathfrak{s}}\in \mathcal{D}$
, for
![]() $\sigma \in \textrm{Gal}(K^{\textrm{s}}/F_{\mathfrak{s}})\subseteq G$
we have
$\sigma \in \textrm{Gal}(K^{\textrm{s}}/F_{\mathfrak{s}})\subseteq G$
we have
![]() $\sigma (w_{\mathfrak{s}})\in \mathcal{D}$
. In particular,
$\sigma (w_{\mathfrak{s}})\in \mathcal{D}$
. In particular,
![]() $v(r-\sigma (w_{\mathfrak{s}}))\geq \rho _{\mathfrak{s}}$
for any
$v(r-\sigma (w_{\mathfrak{s}}))\geq \rho _{\mathfrak{s}}$
for any
![]() $r\in \mathfrak{s}$
. Define
$r\in \mathfrak{s}$
. Define
If
![]() $m=[F_{\mathfrak{s}}[w_{\mathfrak{s}}]:F_{\mathfrak{s}}]$
, then
$m=[F_{\mathfrak{s}}[w_{\mathfrak{s}}]:F_{\mathfrak{s}}]$
, then
![]() $w=\sum _{j=1}^m\sigma _j(w_{\mathfrak{s}})/m$
, where
$w=\sum _{j=1}^m\sigma _j(w_{\mathfrak{s}})/m$
, where
![]() $\sigma _1(w_{\mathfrak{s}}),\dots,\sigma _m(w_{\mathfrak{s}})$
are the roots of the minimal polynomial of
$\sigma _1(w_{\mathfrak{s}}),\dots,\sigma _m(w_{\mathfrak{s}})$
are the roots of the minimal polynomial of
![]() $w_{\mathfrak{s}}$
over
$w_{\mathfrak{s}}$
over
![]() $F_{\mathfrak{s}}$
(with
$F_{\mathfrak{s}}$
(with
![]() $\sigma _j\in \textrm{Gal}(K^{\textrm{s}}/F_{\mathfrak{s}})$
). Since
$\sigma _j\in \textrm{Gal}(K^{\textrm{s}}/F_{\mathfrak{s}})$
). Since
![]() $L/F_{\mathfrak{s}}$
is tamely ramified,
$L/F_{\mathfrak{s}}$
is tamely ramified,
![]() $p\nmid [L:F_{\mathfrak{s}}]$
and so
$p\nmid [L:F_{\mathfrak{s}}]$
and so
![]() $p\nmid m$
. In particular,
$p\nmid m$
. In particular,
![]() $v(m)=0$
and so for any
$v(m)=0$
and so for any
![]() $r\in \mathfrak{s}$
we have
$r\in \mathfrak{s}$
we have
Then
![]() $w\in F_{\mathfrak{s}}$
is a rational centre of
$w\in F_{\mathfrak{s}}$
is a rational centre of
![]() $\mathfrak{s}$
.
$\mathfrak{s}$
.
Appendix B: Dualising sheaf under base extensions
Let
![]() $F/K$
be a finite Galois extension and let
$F/K$
be a finite Galois extension and let
![]() $O_F$
be the ring of integers of
$O_F$
be the ring of integers of
![]() $F$
.
$F$
.
Lemma B.1.
Let
![]() $M$
be a flat
$M$
be a flat
![]() $O_K$
-module and
$O_K$
-module and
![]() $M_F\;:\!=\;M\otimes _{O_K}O_F$
. Then
$M_F\;:\!=\;M\otimes _{O_K}O_F$
. Then
Proof. As
![]() $M$
is flat, the functor
$M$
is flat, the functor
![]() $M\otimes _{O_K}-$
is (left) exact. From the isomorphism
$M\otimes _{O_K}-$
is (left) exact. From the isomorphism
![]() $O_K\simeq O_F^{\textrm{Gal}(F/K)}$
it follows that
$O_K\simeq O_F^{\textrm{Gal}(F/K)}$
it follows that
that is
![]() $M\simeq M_F^{\textrm{Gal}(F/K)}$
, as required.
$M\simeq M_F^{\textrm{Gal}(F/K)}$
, as required.
Proposition B.2.
Let
![]() $C$
be a smooth projective curve of genus
$C$
be a smooth projective curve of genus
![]() $g\geq 1$
and let
$g\geq 1$
and let
![]() $\mathcal{C}$
be a regular model of
$\mathcal{C}$
be a regular model of
![]() $C$
over
$C$
over
![]() $O_K$
. Denote by
$O_K$
. Denote by
![]() $C_F$
and
$C_F$
and
![]() $\mathcal{C}_{O_F}$
the base extended schemes. Then
$\mathcal{C}_{O_F}$
the base extended schemes. Then
![]() $H^0(\mathcal{C}_F,\omega _{\mathcal{C}_F/O_F})\simeq H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})\otimes _{O_K}O_F$
and
$H^0(\mathcal{C}_F,\omega _{\mathcal{C}_F/O_F})\simeq H^0(\mathcal{C},\omega _{\mathcal{C}/O_K})\otimes _{O_K}O_F$
and
Proof. The Lemma follows from the following results: [Reference Liu9, Proposition 10.1.17], [Reference Liu9, Theorem 6.4.9(b)], [Reference Liu9, Exercise 6.4.6], [Reference Liu9, Corollary 5.2.27] and the previous lemma.