Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T09:33:56.197Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Integer Solutions of the Diophantine Equation x2-dy2=1

Published online by Cambridge University Press:  18 May 2009

John Hunter
John Hunter
Affiliation:
The University Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the equation

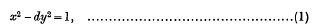
dis any positive integer which is not a perfect square. For convenience we shall consider only those solutions of (1) for which x and yare both positive. All the others can be obtained from these. In fact, it is well known that if (x0, y0) is the minimum positive integer solution of (1), then all integer solutions (x, y) are given by

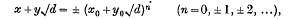
and, in particular, all positive integer solutions are given by

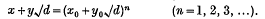
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 3 , Issue 1 , December 1956 , pp. 55 - 56
Copyright
Copyright © Glasgow Mathematical Journal Trust 1956