Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:35:31.486Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SOLVABILITY OF BILINEAR EQUATIONS IN FINITE FIELDS

Published online by Cambridge University Press:  01 September 2008

IGOR E. SHPARLINSKI
IGOR E. SHPARLINSKI*
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia e-mail: igor@ics.mq.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

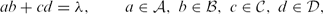
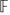
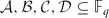We consider the equation over a finite field q of q elements, with variables from arbitrary sets . The question of solvability of such and more general equations has recently been considered by Hart and Iosevich, who, in particular, prove that if for some absolute constant C > 0, then above equation has a solution for any λ ∈ q*. Here we show that using bounds of multiplicative character sums allows us to extend the class of sets which satisfy this property.

Keywords

11L4011T30
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 3 , September 2008 , pp. 523 - 529
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Ahmadi, O. and Shparlinski, I. E., Distribution of matrices with restricted entries over finite fields, Indag. Math. 18 (2007), 327–337.CrossRefGoogle Scholar
2.Bourgain, J., Glibichuk, A. A. and Konyagin, S. V., Estimates for the number of sums and products and for exponential sums in fields of prime order, J. Lond. Math. Soc. 73 (2006), 380–398.CrossRefGoogle Scholar
3.Bourgain, J., Katz, N. and Tao, T., A sum product estimate in finite fields and applications, Geom. Funct. Anal. 14 (2004), 27–57.CrossRefGoogle Scholar
4.Garaev, M. Z., An explicit sum–product estimate in p, Intern. Math. Res. Notices 2007 (2007), 1–11 (article ID rnm035).Google Scholar
5.Garaev, M. Z., The sum–product estimate for large subsets of prime fields, Proc. Amer. Math. Soc. 136 (2008), 2735–2739.CrossRefGoogle Scholar
6.Garaev, M. Z. and Garcia, V., The equation x 1x 2 = x 3x 4 + λ in fields of prime order and applications, J. Number Theory, 2007.Google Scholar
7.Gyarmati, K. and Sárközy, A., Equations in finite fields with restricted solution sets, I (Character sums), Acta Math. Hungar. 118 (2008), 129–148.CrossRefGoogle Scholar
8.Gyarmati, K. and Sárközy, A., Equations in finite fields with restricted solution sets, II (Algebraic equations), Acta Math. Hungar 119 (2008), 259–280.CrossRefGoogle Scholar
9.Hart, D. and Iosevich, A., Sums and products in finite fields: An integral geometric viewpoint, Contemp. Mathem. (in press).Google Scholar
10.Hart, D., Iosevich, A., Koh, D. and Rudnev, M., Averages over hyperplanes, sum–product theory in finite fields, and the Erdos–Falconer distance conjecture, Preprint, 2007 (available from http:/!/arxiv.org/abs/0707.3473).Google Scholar
11.Hart, D., Iosevich, A. and Solymosi, J., Sums and products in finite fields via Kloosterman Sums, Intern. Math. Res. Notices 2007 (2007), 1–14 (article ID rnm007).Google Scholar
12.Friedlander, J. and Iwaniec, H., Estimates for character sums, Proc. Amer. Math. Soc. 119 (1993), 363–372.CrossRefGoogle Scholar
13.Karatsuba, A. A., The distribution of values of Dirichlet characters on additive sequences, Doklady Acad. Sci. USSR 319 (1991), 543–545 (in Russian).Google Scholar
14.Karatsuba, A. A., Basic analytic number theory (Springer-Verlag, Berlin, 1993).CrossRefGoogle Scholar
15.Katz, N. H. and Shen, C.-Y., Garaev's inequality in finite fields not of prime order, J. Anal. Combin. 3 (2008).Google Scholar
16.Katz, N. H. and Shen, C.-Y., A slight improvement to Garaev's sum product estimate, Proc. Amer. Math. Soc. 136 (2008), 2499–2504.CrossRefGoogle Scholar
17.Lidl, R. and Niederreiter, H., Finite fields (Cambridge University Press, Cambridge, UK, 1997).Google Scholar
18.Sárközy, A., On sums and products of residues modulo p, Acta Arith. 118 (2005), 403–409.CrossRefGoogle Scholar
19.Sárközy, A., On products and shifted products of residues modulo p, Integers (in press).Google Scholar
20.Shparlinski, I. E., Bilinear character sums over elliptic curves, Finite Fields Their Appl. 14 (2008), 132–141.CrossRefGoogle Scholar
21.Vinogradov, I. M., Elements of number theory (Dover Publications, NY, 1954).Google Scholar