Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:43:21.594Z Has data issue: false hasContentIssue false
  • English
  • Français

SCHOTTKY UNIFORMIZATIONS OF SYMMETRIES

Published online by Cambridge University Press:  25 February 2013

G. GROMADZKI  and
R. A. HIDALGO
G. GROMADZKI
Affiliation:
Institute of Mathematics, University of Gdansk, Poland e-mail: greggrom@math.univ.gda.pl
R. A. HIDALGO
Affiliation:
Departamento de Matemática, Universidad Técnica Federico Santa María, Valparaíso, Chile e-mail: ruben.hidalgo@usm.cl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A real algebraic curve of genus g is a pair (S,〈 τ 〉), where S is a closed Riemann surface of genus g and τ: S → S is a symmetry, that is, an anti-conformal involution. A Schottky uniformization of (S,〈 τ 〉) is a tuple (Ω,Γ,P:Ω → S), where Γ is a Schottky group with region of discontinuity Ω and P:Ω → S is a regular holomorphic cover map with Γ as its deck group, so that there exists an extended Möbius transformation 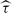$\widehat{\tau}$ keeping Ω invariant with P o 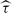$\widehat{\tau}$=τ o P. The extended Kleinian group K=〈 Γ, 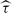$\widehat{\tau}$〉 is called an extended Schottky groups of rank g. The interest on Schottky uniformizations rely on the fact that they provide the lowest uniformizations of closed Riemann surfaces. In this paper we obtain a structural picture of extended Schottky groups in terms of Klein–Maskit's combination theorems and some basic extended Schottky groups. We also provide some insight of the structural picture in terms of the group of automorphisms of S which are reflected by the Schottky uniformization. As a consequence of our structural description of extended Schottky groups, we get alternative proofs to results due to Kalliongis and McCullough (J. Kalliongis and D. McCullough, Orientation-reversing involutions on handlebodies, Trans. Math. Soc. 348(5) (1996), 1739–1755) on orientation-reversing involutions on handlebodies.

Keywords

30F1030F4030F50
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 3 , September 2013 , pp. 591 - 613
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Ahlfors, L. and Sario, L., Riemann surfaces (Princeton University Press, Princeton NJ, 1960).CrossRefGoogle Scholar
2.Alling, N. and Greenleaf, N., Foundations of the theory of Klein surfaces, Lecture Notes in Mathematics, vol. 219 (Springer, Berlin, Germany, 1971).Google Scholar
3.Bujalance, E., Cirre, J. F., Gamboa, J. M. and Gromadzki, G., Symmetries of compact Riemann surfaces, Lecture Notes in Mathematics vol. 2007 (Springer-Verlag, Berlin, Germany, 2010).CrossRefGoogle Scholar
4.Greenberg, L., Maximal Fuchsian Groups. Bull. AMS 69 (1963), 569–573.CrossRefGoogle Scholar
5.Gromadzki, G., On a Harnack-Natanzon theorem for the family of real forms of Riemann surfaces, J. Pure Appl. Algebra 121 (1997), 253–269.CrossRefGoogle Scholar
6.Harnack, A., Ueber die Vieltheiligkeit der ebenen algebraischen Curven, Math. Ann. 10 (2) (1876), 189–198.Google Scholar
7.Heltai, B., Symmetric Riemann surfaces, torsion subgroups and Schottky coverings, Proc. Am. Math. Soc. 100 (1987), 675–682.Google Scholar
8.Hidalgo, R. A., Automorphisms groups of Schottky type, Ann. Acad. Sci. Fenn. 30 (2005), 183–204.Google Scholar
9.Hidalgo, R. A., Maximal Schottky extension groups, Geometriae Dedicata 146 (1) (2010), 141–158.Google Scholar
10.Hidalgo, R. A., An equivariant loop theorem for Kleinian groups: A decomposition structure of extended function groups (Preprint).Google Scholar
11.Hidalgo, R. A. and Maskit, B., On Klein–Schottky groups, Pacific J. Math. 220 (2) (2005), 313–328.CrossRefGoogle Scholar
12.Hidalgo, R. A. and Maskit, B., A note on the lifting of automorphisms. in Geometry of Riemann surfaces. Lecture Notes of the London Mathematics Society, vol. 368 (Fred, G., Gabino, G. and Christos, K., Editors) (Cambridge University Press, Cambridge, UK, 2010), 260–267. ISBN-13-9780521733076.Google Scholar
13.Kalliongis, J. and McCullough, D., Orientation-reversing involutions on handlebodies, Trans. Math. Soc. 348 (5) (1996), 1739–1755.CrossRefGoogle Scholar
14.Klein, F., Über Realitätsverhältnisse bei der einem beliebigen Geschlechte zugehörigen Normalkurve der φ. Math. Annalen 42 (1) (1893), 1–29.CrossRefGoogle Scholar
15.Macbeath, A. M., The classification of non-Euclidean crystallographic groups, Canad. J. Math. 19 (1967), 1192–1205.CrossRefGoogle Scholar
16.Macbeath, A. M. and Singerman, D., Spaces of subgroups and Teichmüller space, Proc. Lond. Math. Soc. 31 (3) (1975), 211–256.Google Scholar
17.Maskit, B., Construction of Kleinian groups, in Proc. of the conf. on complex anal., Minneapolis, 1964 (Aeppli, A., Calabi, E. and Röhrl, H., Ediors) (Springer-Verlag, Berlin, Germany, 1965), 281–296.Google Scholar
18.Maskit, B., A characterization of Schottky groups, J. d'Analyse Math. 19 (1967), 227–230.Google Scholar
19.Maskit, B., The conformal group of a plane domain, Amer. J. Math. 90 (3) (1968), 718–722.Google Scholar
20.Maskit, B., On Klein's combination theorem III. Advances in the theory of Riemann surfaces (Proc. of Conf., Stony Brook, NY, 1969), Ann. Math. Stud. 66 (1971), 297–316 (Princeton University Press).Google Scholar
21.Maskit, B., Decomposition of certain Kleinian groups, Acta Math. 130 (1973), 243–263.Google Scholar
22.Maskit, B., On the classification of Kleinian groups. I. Koebe groups, Acta Math. 135 (1975), 249–270.CrossRefGoogle Scholar
23.Maskit, B., On the classification of Kleinian Groups. II. Signatures, Acta Math. 138 (1976), 17–42.Google Scholar
24.Maskit, B., Kleinian groups GMW (Springer-Verlag, Berlin, Germany, 1987).CrossRefGoogle Scholar
25.Maskit, B., On Klein's combination theorem. IV. Trans. Am. Math. Soc. 336 (1993), 265–294.Google Scholar
26.Matsuzaki, K. and Taniguchi, M., Hyperbolic manifolds and Kleinina groups, Oxford Mathematical Monographs, Oxford Science Publications (Clarendon Press, Oxford University Press, New York, 1998).Google Scholar
27.Meeks, W. H. III and Yau, S.-T., Topology of three-dimensional manifolds and the embedding problem in minimal surface theory. Ann. Math. 112 (2) (1980), 441–484.CrossRefGoogle Scholar
28.Natanzon, S. M., Differential equations for Prym theta-functions. A criterion for two-dimensional finite zone potential Schrödinger operators to be real, Funktsional Anal. i Prilozhen 26 (1992), 17–26. (English translation in Funct. Anal. Appl. 26 (1992), 13–20.)CrossRefGoogle Scholar
29.Sibner, R. J., Symmetric Fuchsian groups, Am. J. Math. 90 (1968), 1237–1259.Google Scholar
30.Singerman, D., Finitely maximal Fuchsian groups, J. Lond. Math. Soc. 6 (2) (1972), 29–38.CrossRefGoogle Scholar
31.Stephanus, M., Orientation reversing involutions of a handlebody Dissertation (St. Louis University, St. Louis, MO, 1995).Google Scholar
32.Zimmermann, B., Über Homöomorphismen n-dimensionaler Henkelkörper und endliche Erweiterungen von Schottky-Gruppen (German), [On homeomorphisms of n-dimensional handlebodies and on finite extensions of Schottky groups] Comment. Math. Helv. 56 (1981), no. 3, 474–486.Google Scholar
33.Zimmermann, B., Finite maximal orientation reversing group actions on handlebodies and 3-manifolds, Rend. Circ. Mat. Palermo (2) 48 (3) (1999), 549–562.Google Scholar