Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T10:55:11.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Semi-field-like affine planes

Published online by Cambridge University Press:  18 May 2009

Michael J. Kallaher
Michael J. Kallaher
Affiliation:
Universität Kaiserslautern, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Walker [11] describes a new class of translation planes W(q) of order q2, q ≡ 5(mod 6), with kernel GF(q). A plane in this class has several interesting properties, but we shall be only interested in the following ones possessed by its collineation group G: (i) G is transitive on the affine points of W(q), and (ii) G fixes a point 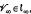the line at infinity of W(q), and is transitive on the other points of l∞ The smallest member of this class, W(5), also satisfies: (iii) for an affine point 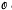the subgroup G 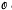is transitive on the affine points ≠ 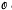of the line 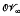Note also that since W(5) is a translation plane, replacing G with G 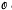in (ii) we get a fourth property, call it (iv), satisfied by G. (See Lemma 2.)

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 18 , Issue 2 , July 1977 , pp. 113 - 123
Copyright
Copyright © Glasgow Mathematical Journal Trust 1977

References

REFERENCES

1.Albert, A. A., On the coUineation groups associated with twisted fields, Calcutta Math. Soc. Golden Jubilee Commemoration volume, Part II (1958/1959), 485–497.Google Scholar
2.Andre', J., Über Perspektivitaten in endlichen projektiven Ebenen, Arch. Math. (Basel) 6 (1954), 29–32.CrossRefGoogle Scholar
3.Dembowski, P., Finite Geometries (Springer-Verlag, 1968).CrossRefGoogle Scholar
4.Hering, C., On 2-groups operating on projective planes, Illinois J. Math. 16 (1972), 581–595.CrossRefGoogle Scholar
5.Huppert, B., Zweifach transitive, auflosbare Permutations-gruppen, Math. Z. 68 (1957), 126–150.CrossRefGoogle Scholar
6.Johnson, N. J. and Kallaher, M. J., Transitive collineation groups on affine planes, Math. Z. 135 (1973), 149–164.CrossRefGoogle Scholar
7.Kallaher, M. J., Rank 3 affine planes of square order, Geometriae Dedicata 1 (1973), 415–425.CrossRefGoogle Scholar
8.Kallaher, M. J. and Ostrom, T. G., Fixed-point-free linear groups, rank three planes, and Bol quasi-fields, J. Algebra 18 (1971), 159–178.CrossRefGoogle Scholar
9.Ostrom, T. G., Finite Translation Planes (Springer-Verlag, 1971).Google Scholar
10.Ostrom, T. G., Classification of finite translation planes, Proc. Internal. Confer, on Projective Planes, Pullman, WA. (1973), 195–213.Google Scholar
11.Walker, M., On translation planes and their collineation groups, Thesis, Westfield College, University of London (1973).Google Scholar
12.Wielandt, H., Finite Permutation Groups (Academic Press, 1964).Google Scholar
13.Zsigmondy, K., Zur Theorie der Potenzreste, Monatsh. Math. Phys. (1892), 265–284.CrossRefGoogle Scholar