Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fennessey, Eric J.
and
Pride, Stephen J.
1989.
Equivalences of two-complexes, with applications to NEC-groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 106,
Issue. 2,
p.
215.
Pride, Stephen J
1989.
Involutary presentations, with applications to Coxeter groups, NEC-groups, and groups of Kanevskiĭ.
Journal of Algebra,
Vol. 120,
Issue. 1,
p.
200.
Pride, Stephen J.
1989.
Groups — Korea 1988.
Vol. 1398,
Issue. ,
p.
146.
Duncan, Andrew J.
and
Howie, James
1991.
The genus problem for one-relator products of locally indicable groups.
Mathematische Zeitschrift,
Vol. 208,
Issue. 1,
p.
225.
Duncan, Andrew J.
and
Howie, James
1991.
The nonorientable genus problem for one-relator products.
Communications in Algebra,
Vol. 19,
Issue. 9,
p.
2547.
Howie, James
1991.
Nonsingular systems of two length three equations over a group.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 1,
p.
11.
Bogley, W. A.
and
Pride, S. J.
1992.
Aspherical relative presentations.
Proceedings of the Edinburgh Mathematical Society,
Vol. 35,
Issue. 1,
p.
1.
Corson, J. M.
1995.
Howie diagrams and complexes of groups.
Communications in Algebra,
Vol. 23,
Issue. 14,
p.
5221.
Brick, Stephen G.
and
Corson, Jon M.
1998.
Annular Dehn functions of groups.
Bulletin of the Australian Mathematical Society,
Vol. 58,
Issue. 3,
p.
453.
Pride, S. J.
and
Wang, Jing
2000.
Subgroups of finite index in groups with finite complete rewriting systems.
Proceedings of the Edinburgh Mathematical Society,
Vol. 43,
Issue. 1,
p.
177.
Juhász, Arye
2003.
On powered one-relator HNN-extensions of groups.
Journal of Group Theory,
Vol. 6,
Issue. 4,
Wise, Daniel
2003.
Nonpositive immersions, sectional curvature, and subgroup properties.
Electronic Research Announcements of the American Mathematical Society,
Vol. 9,
Issue. 1,
p.
1.
Hruska, G Christopher
2004.
Nonpositively curved 2–complexes with isolated flats.
Geometry & Topology,
Vol. 8,
Issue. 1,
p.
205.
JUHÁSZ, ARYE
2006.
SOME REMARKS ON ONE-RELATOR AMALGAMATED FREE PRODUCTS II.
International Journal of Algebra and Computation,
Vol. 16,
Issue. 01,
p.
1.
Wang, Xiaofeng
Xie, Wanwen
and
Bao, Xiaomin
2007.
Trivializers and 2-Complexes.
Algebra Colloquium,
Vol. 14,
Issue. 03,
p.
443.
Juhász, Arye
2007.
Geometric Group Theory.
p.
121.
Howie, James
and
Williams, Gerald
2012.
Tadpole Labelled Oriented Graph groups and cyclically presented groups.
Journal of Algebra,
Vol. 371,
Issue. ,
p.
521.
Klyachko, Anton A.
and
Lurye, Denis E.
2012.
Relative hyperbolicity and similar properties of one-generator one-relator relative presentations with powered unimodular relator.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 3,
p.
524.
WILLIAMS, GERALD
2012.
GROUPS OF FIBONACCI TYPE REVISITED.
International Journal of Algebra and Computation,
Vol. 22,
Issue. 08,
p.
1240002.
Keller, Matthias
Peyerimhoff, Norbert
and
Pogorzelski, Felix
2017.
Sectional curvature of polygonal complexes with planar substructures.
Advances in Mathematics,
Vol. 307,
Issue. ,
p.
1070.

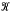 ⃗ℒ (”strong mappings”) one gets an induced mapping φ
⃗ℒ (”strong mappings”) one gets an induced mapping φ