Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T06:52:05.287Z Has data issue: false hasContentIssue false
  • English
  • Français

WEYL'S THEOREM FOR CLASS A(k) OPERATORS

Published online by Cambridge University Press:  01 January 2008

J. STELLA IRENE MARY  and
S. PANAYAPPAN
J. STELLA IRENE MARY
Affiliation:
Department of Mathematics, PSG College of Arts and Science, Coimbatore-641014, India e-mail: stellairenemary@gmail.com
S. PANAYAPPAN
Affiliation:
Department of Mathematics, Government Arts College, Coimbatore-641018, India e-mail: panayappan@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall show that Weyl's theorem holds for class A(k) operators T where k≥>1, via its hyponormal transform 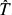. Next we shall prove some applications of Weyl's theorem on class A(k) operators.

Keywords

47A1347A63
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 1 , January 2008 , pp. 39 - 46
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Aiena, P. and Carpintero, C., Weyl's theorem, α- Weyl's theorem and single valued extension property, Extracta Math. 20 (2005), 25–41.Google Scholar
2.Aluthge, A., Some generalised theorems on p-hyponormal operators, Int. Eq. 0p. Th. 24 (1996), 497–501.CrossRefGoogle Scholar
3.Berberian, S. K., An extension of Weyl's theorem to a class of not necessarily normal operators, Michigan Math. J. 16 (1969), 273–279.CrossRefGoogle Scholar
4.Cho, M., Itoh, M. and Oshiro, S., Weyl's theorem holds for p-hyponormal operators, Glasgow Math. J. 39 (1997), 217–220.CrossRefGoogle Scholar
5.Cho, M. and Yamazaki, T., An operator transform from class A to the class of hyponormal operators and its application, Int. Eq. 0p. Th. 53 (2005), 497–508.CrossRefGoogle Scholar
6.Chourasia, N. N. and Ramanujan, P. B., Paranormal operators on Banach space, Bull. Austral. Math. Soc. 21 (1980), 161–168.CrossRefGoogle Scholar
7.Coburn, L. A., Weyl's theorem for nonnormal operators, Michigan Math. J. 13 (1966), 285–288.CrossRefGoogle Scholar
8.Curto, R. E. and Han, Y. M., Weyl's theorem, a-Weyl's theorem and local spectral theory, J. London Math. Soc. (2) 67 (2003), 499–509.CrossRefGoogle Scholar
9.Curto, R. E. and Han, Y. M., Weyl's theorem for algebraically paranormal operators, Int. Eq. 0p. Th. 47 (2003), 307–314.CrossRefGoogle Scholar
10.Duggal, B. P. and Kubrusly, C., Weyl's theorems for posinormal operators, J. Korean. Math. Soc. 42 (2005), 529–541.CrossRefGoogle Scholar
11.Duggal, B. P., Jeon, I. H. and Kim, I. H., On Weyl's theorem for quasi-class A operators, J. Korean. Math. Soc. 43 (2006), 899–909.CrossRefGoogle Scholar
12.Fujii, M., Jung, D., Lee, S. H., Lee, M. Y. and Nakamoto, Some class of operators related to paranormal and log-hyponormal operators, Math. Japan. 51 (2000), 395–402.Google Scholar
13.Furuta, T., Ito, M. and Yamazaki, T., A subclass of paranormal operators including class of log-hyponormal and several related classes, Sci. Math. 1 (1998), 389–403.Google Scholar
14.Han, Y. M. and Lee, W. Y., Weyl's theorem holds for algebraically hyponormal operators Proc. Amer. Math. Soc. 128 (2000), 2291–2296.CrossRefGoogle Scholar
15.Han, Y. M. and Lee, W. Y., Weyl spectra and Weyl's theorem, Studia Math. 148 (2001), 193–206.CrossRefGoogle Scholar
16.Hansen, F., An inequality, Math. Ann. 246 (1980), 249–250.CrossRefGoogle Scholar
17.Ito, M. and Yamazaki, T., Relations between two inequalities and and their applications, Int. Eq. Op. Th. 44 (2002), 442–450.CrossRefGoogle Scholar
18.Mary, J. S. I. and Panayappan, S., Some properties of class A(k) operators and their hyponormal transforms, Glasgow Math. J. 49 (2007), 133–143.CrossRefGoogle Scholar
19.Mechrei, S., Weyl's theorem for algebraically class A operators, Bull. Belg. Math. Soc. Simon Stevin 14 (2007), 239–246.Google Scholar
20.Stampfli, J., Hyponormal operators, Pacific J. Math. 12 (1962), 1453–1458.CrossRefGoogle Scholar
21.Uchiyama, A., Weyl's theorem for class A operators, Math.Inequal. Appl. 4 (2001), 143–150.Google Scholar
22.Yamazaki, T., On powers of class A(k) operators including p-hyponormal and log hyponormal operators, Math. Inequal. Appl. 3 (2000), 97–104.Google Scholar