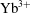Defining the optimal gradient doped $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{Yb}^{3+}$:YAG disk for room and low temperature diode pumped solid-state laser operations

Abstract

We propose a general methodology to define the optimum doping ion volume distribution required for an efficient solid-state laser amplifier. This approach is illustrated in the context of two experimental diode pumped Yb:YAG amplifiers operating at 300 and 160 K. Processing of such tailored gain media is now possible through horizontal direct crystallization.

1. Introduction

The elaboration and processing of yttrium aluminum garnet ${\rm Y}_{3}{\rm Al}_{5}{\rm O}_{12}$ (YAG) laser crystals with controlled spatial distribution of ${\rm Yb}^{3+}$ ions has been demonstrated with the horizontal direct crystallization (HDC) technique known as the Bagdasarov growth method^[1]. HDC grown Yb:YAG disks as large as 77 mm have been produced, as illustrated in Figure 1. The advantages offered by such non-homogeneously doped structures in terms of both thermal and amplified spontaneous emission (ASE) management have been revealed in the context of disk amplifiers used in an active mirror architecture^[2], where pumping and extraction take place on one side (AR coated) of the disk whereas cooling occurs on the other side (HR coated).

We detail here a methodology to define the optimum doping ion volume distribution required for two diode pumped Yb:YAG amplifiers. The proposed approach requires one first to define a convenient workspace to easily quantify the lasing ion distribution in an HDC engineered gain medium of thickness $t$ (see Figure 1(a)). Since the doping distributions obtained with this growth technique are very linear^{[1, 2]}, we shall consider $g_{d}$ [at.%], the doping linear ramp, as the first relevant quantity (horizontal axis). $g_{d} / t$ is the actual gradient, expressed in at.% ${\rm cm}^{-1}$. The second quantity is the average doping level $d_{0}$ [at.%] (vertical axis), which corresponds to the doping level at half the thickness of the considered disk, $d_{0}=d(t/2)$. A disk is therefore defined in a two-dimensional [$g_{d},d_{0}$] workspace limited by the blue triangle in Figure 1.

Figure 1. (a) The workspace defined by the disk doping ramp over its thickness and the doping mean value. (b) The linear doping equation $d(x)=d_{0}+g_{d}(x-t/2)/t$. The inset shows the 77 mm disk used for the 160 K Lucia active mirror amplifier; it corresponds to the blue circle with coordinates (0, 1) in the workspace; the other circle (0, 2) refers to the 300 K disk. Both positions are qualified as WP.

Figure 2. The thermal evolution of the absorption cross section between 90 and 300 K for an HDC grown homogeneously 1 at.% doped 1 cm thick Yb:YAG crystal. The data in (a) are collected at 940 nm whereas those in (b) correspond to the 1030 nm absorption peak. The red dots refer to data from Fan^[7] whereas the green ones refer to data from Brown^[8].

We consider two experimental cases corresponding to the two power amplifiers of the Lucia laser project^[3] at the Laboratoire pour l’Utilisation des Laser Intenses (LULI) of the Ecole Polytechnique, Palaiseau, France. In its current configuration this diode pumped solid-state laser (DPSSL) relies on two homogeneously doped Yb:YAG disks. Apart from having different dimensions and doping, the main differentiating feature is the operation temperature. Whereas the first amplifying stage operates at room temperature (300 K) and is water cooled^[3], the second active mirror amplifier is designed to operate at a much colder temperature (160 K), cooled with an innovative helium cell^[4].

Section 2 gives the respective cross sections used in the model derived to optimize the YAG disks’ axial gradient in Yb concentration.

The 300 K amplifier disk is 60 mm in diameter and 7 mm thick, homogeneously doped at 2 at.%, defining a working point WP with coordinates ($g_{d}=0$ at.%, $d_{0}=2$ at.%) in our workspace. The optimum point OP identification is detailed in Section 3, relying on stored energy and gain calculated through the Frantz and Nodvik formalism^[5].

The 160 K amplifier disk is 77 mm in diameter and 10 mm thick, homogeneously doped at 1 at.%, defining a WP with coordinates ($g_{d}=0$ at.%, $d_{0}=1$ at.%). The OP identification is detailed in Section 4.

2. Absorption cross sections

The Lucia DPSSL currently operates two active mirror amplifiers at 300 and 160 K. In both cases, the gain medium is a YAG disk whose thickness and doping level have been optimized to maximize the laser efficiency considering a homogeneous volume distribution of Yb ions. The Lucia cryogenic amplifier relies on a thin (sub-mm) layer of helium for heat extraction^{[3, 6]} through the HR coated surface of the active mirror. The helium layer thermal conductivity is adjusted through careful pressure control, allowing the absorption to be recorded over a 90 to 300 K temperature range, as illustrated in Figure 2. The cross sections considered in our model are reported in Table 1, the absorption cross sections being our measurements while the emission ones are taken from the literature^{[7, 8]}.

Table 1. Absorption and emission cross sections at 300 and 160 K.

Figure 3. Stored energy density map versus doping ramp and mean value. For each specific doping ramp, a minimum average doping value exists below which this doping ramp is not defined; this explains the map’s white triangular area. The iso-energy density $9\ {\rm J}\ {\rm cm}^{-2}$ line above which the requested energetic performance will be reached is drawn.

3. Optimum Yb:YAG disk for a 300 K amplifier

The Lucia laser chain room temperature operated amplifier has previously been detailed^[3]. The gain medium is an Yb:YAG disk 60 mm in diameter and 7 mm thick homogeneously doped at 2 at.%. It is pumped at a maximum level of $16\ {\rm kW}\ {\rm cm}^{-2}$ over an area limited to 30 mm in diameter in order to take advantage of the 1030 nm absorption to mitigate ASE parasitic oscillations (Figure 16 of Ref. [3]). The relevant dimension to consider for ASE management is therefore $L_{\rm ASE} = 30$ mm. Considering the well-known limit for the constraint $g_{0}L_{\rm ASE}\le 4$, the maximum allowed value for the small signal gain is $g_{0,{\rm max}}=1.33\ {\rm cm}^{-1}$. Wherever in the gain medium the gain exceeds this threshold, one enters into a regime where parasitic oscillations will start to deplete the gain.

Let us consider the workspace defined in Section 1 by the doping linear ramp $g_{d}$ and the average doping level $d_{0}$. Extreme values of $g_{d}$ are set from 0 to 8 at.% along the disk thickness of 7 mm. This means that the maximum explored gradient reaches 11.4 at.% ${\rm cm}^{-1}$. Extreme values of $d_{0}$ are set from 0 to 4 at.%. The Lucia current room temperature operated crystal is then defined in this space by a WP whose coordinates are ($g_{d}=0$ at.%, $d_{0}=2$ at.%). Let us first consider how the stored energy density (${\rm J}\ {\rm cm}^{-2}$) is distributed in this workspace (Figure 3). The WP is materialized by the blue circle and we observe an energy density of 9 ${\rm J}\ {\rm cm}^{-2}$. The corresponding iso-energy density line is drawn on the map as well. It defines a boundary below which the Lucia room temperature energetic performance would not be satisfied. It is remarkable to observe that above this frontier, an increase in the average doping affects the energy density only very moderately, whereas below this line it decreases very rapidly. The WP has then been defined to be set on the edge of this plateau.

Figure 4. (a) Maximum gain map versus doping ramp and mean value. The 1.33 ${\rm cm}^{-1}$ threshold iso-gain curve is drawn in solid back. Below this value, ASE triggered parasitic oscillations are expected to be severely limited, guaranteeing a satisfactory efficiency for the amplifier. The iso-energy density $9\ {\rm J}\ {\rm cm}^{-2}$ line is also drawn (dashed line). The bottom right inset gives an enlarged view of the AoI. (b) Small signal gain distribution over the 7 mm thick crystal for the current 2 at.% constant doped crystal (black) and optimum 1.9 at.% average/0.9 at.% doping ramp crystal (red).

Figure 5. (a) Gain contrast $Cg_{0}$ map versus doping ramp and mean value. The red rectangle gives the AoI. The iso-energy density $9\ {\rm J}\ {\rm cm}^{-2}$ line is dashed. The optimum region is white dashed. The Lucia current operating point WP is marked with the blue circle (27%) and the optimum one is marked in yellow (2.4%). (b) The gain profiles for the blue and yellow points.

This map is obtained without considering ASE losses. In practice, increasing the doping mean value far above 2 at.% would actually not lead to a continuous increase of the stored energy density because at some point the gain medium would start seeing its gain being depleted by ASE related deleterious effects. We have defined such a threshold while introducing $g_{0,{\rm max}}=1.33\ {\rm cm}^{-1}$. A maximum gain value map was then derived to identify the safe operation area within the workspace (Figure 4(a)). To derive this map, for each ($g_{d}$, $d_{0}$) point, the gain axial variation $g_{0}(z)$ is first computed. In Figure 4(b), two of these curves are given, the black one for WP. The maximum value of each curve, ${\rm Max}[g_{0}(z)]$, is then simply reported on the map.

On this map, the $1.33\ {\rm cm}^{-1}$ threshold iso-gain curve (solid back) is reported together with the $9\ {\rm J}\ {\rm cm}^{-2}$ iso-energy density line, the first defining an upper boundary and the second the lower frontier of a small optimum region (dashes). The inset gives an enlarged view of the area of interest (AoI) within which this optimum region falls. The Lucia current WP is marked with the blue circle $(1.73\ {\rm cm}^{-1})$ whereas the OP (offering the lower $g_{0,{\rm max}} =1.29\ {\rm cm}^{-1}$) is marked in yellow.

Obtaining an axial gain distribution as homogeneous as possible helps in staying below the parasitic oscillation threshold whatever the depth into the gain medium and reduces the gain medium internal stresses induced by the thermal load^[2].

In order to identify the area of best homogeneity, it is convenient to study the gain contrast, defined as $Cg_{0}=(g_{0}^{\rm max}-g_{0}^{\rm min})/(g_{0}^{\rm max}+g_{0}^{\rm min})$. The map of Figure 5 gives the $Cg_{0}$ distribution. As a reference, the AoI rectangle is also displayed as well as the $9\ {\rm J}\ {\rm cm}^{-2}$ iso-energy density line and both the WP and the OP. We observe a very low 2.4% contrast for the OP, a situation noticeably better than the 27% value for the WP.

Figure 6. (a) Stored energy density map versus doping ramp and mean value. (b) Maximum gain map versus doping ramp and mean value. The optimum region (dashed) is defined by an upper boundary: the $1.32\ {\rm cm}^{-1}$ threshold iso-gain curve. Below this value, ASE triggered parasitic oscillations are expected to be severely limited, guaranteeing a satisfactory efficiency for the amplifier. The iso-energy density $3.3\ {\rm J}\ {\rm cm}^{-2}$ line defines the lower boundary. The Lucia low temperature amplifier operating point is marked with the blue circle (0, 1). The yellow circle is located at the lowest gain position along the $3.3\ {\rm J}\ {\rm cm}^{-2}$ energy density line.

Figure 7. (a) Gain contrast $Cg_{0}$ versus doping ramp and mean value. The unity contrast line defines the frontier of doping domains where the minimum gain becomes negative due to strong 1030 nm absorption ($d_{0}> 2.2$ at.%). (b) Gain (bold curves, left scale) and ${\rm Yb}^{3+}$ concentration (dashed lines, right scale) distributions within three 1 cm thick crystals. The respective extreme doping values are given in the inset. The grayed-out bottom area defines the negative gain location.

4. Optimum Yb:YAG disk for a 160 K amplifier

The Lucia low temperature amplifier hosts a 10 mm thick, 1 at.% doped Yb:YAG disk. It is 77 mm wide but pumped over a $23.4\ {\rm mm} \times 30.3\ {\rm mm}$ elliptical surface, leading to a $g_{0,{\rm max}}=1.32\ {\rm cm}^{-1}$ similar to the previous 300 K case. At Lucia working point coordinates (0 at.%, 1 at.%), the stored energy density is $3.3\ {\rm J}\ {\rm cm}^{-2}$. Figure 6(a) gives the stored energy density (${\rm J}\ {\rm cm}^{-2}$) map for the explored region. The iso-energy density $3.3\ {\rm J}\ {\rm cm}^{-2}$ line is shown on the map. It defines a boundary below which the Lucia low temperature energetic performance would not be satisfied. We observe here also that this boundary is set on the edge of an energy density plateau culminating at a $3.5\ {\rm J}\ {\rm cm}^{-2}$ energy density as shown by the 3.4, 3.42, and $3.44\ {\rm J}\ {\rm cm}^{-2}$ iso-energy density curves.

Like for the 300 K case, a maximum gain value map is derived to identify the ASE-compatible area (Figure 6(b)). The $1.32\ {\rm cm}^{-1}$ threshold iso-gain curve (solid back) is reported together with the $3.3\ {\rm J}\ {\rm cm}^{-2}$ iso-energy density line, the first one defining an upper boundary and the second one the lower frontier of the optimum region (dashes). Since the Lucia low temperature amplifier was designed to satisfy the $g_{0}L_{\rm ASE}\le 4$ criterion as closely as possible, the associated WP (blue circle) obviously falls in the vicinity of the $1.32\ {\rm cm}^{-1}$ curve: its value is $1.41\ {\rm cm}^{-1}$. With respect to ASE, a more optimum point marked in yellow can be identified where the maximum gain falls to $0.88\ {\rm cm}^{-1}$. At the other extremity of the optimum region, it is possible to slightly improve the energy storage to reach $3.5\ {\rm J}\ {\rm cm}^{-2}$ if we accept an increased level of ASE losses and, more critically, to the extent of a four times stronger doping gradient and two times higher average doping level! Finally, Figure 7 reveals that in this area the gain contrast $Cg_{0}$ is extremely bad, of the order of 100%, a value that would cause severe issues in terms of heat load thermal management. The value of $Cg_{0}$ is 10% for the OP (yellow circle), while it is 46% for the current configuration (blue circle).

At first sight, it can be surprising to observe that, above a 2.2 at.% average ${\rm Yb}^{3+}$ concentration, we enter into a greater-than-100%-contrast regime for the gain. In order to explain this phenomenon, let us consider a specific point located where $Cg_{0}$ reaches a value above 150%: the green circle of (6 at.%, 3.5 at.%) coordinates. Such a 1 cm crystal would present a 0.5 at.% doped entrance face to the pumping beam while the cooled side would exhibit a 6.5 at.% concentration, as illustrated on the graph of Figure 7 (blue dashed line with the right scale).

As a reference, the 1 at.% ${\rm cm}^{-1}$ yellow OP crystal gradient is also displayed (0.5 to 1.5 at.%, red dashed line) as well as the 1 at.% constant doping distribution (WP, black dashed line). The three bold curves give the associated gain distributions within the 1 cm crystals’ thicknesses. As expected, the red gain curve is very flat with a 10% contrast and the black Lucia low temperature amplifier curve illustrates the 46% contrast resulting from the stronger population inversion located at the pumped face of a constant doped crystal. The blue gain distribution shows that a strong population inversion takes place 2 to 3 mm after the pump entrance face of the (6 at.% ${\rm cm}^{-1}$, 3.5 at.%) crystal. For such a high average doping level (3.5 at.%), this crystal is too thick. Indeed, the last 3 mm of the crystal are actually absorbing (negative gain) the 1030 nm light. This negative gain area is grayed out on the graph. Having such a negative minimum value for the gain explains why the contrast $Cg_{0}$ (as defined) exceeds the 100% value.

Table 2. Energetic improvement for the low temperature amplifier.

5. Parametric study

Higher values of stored energies might be achieved by choosing the appropriate combination of pump power, doping mean value $d_{0}$ and doping ramp $g_{d}$. This obviously influences also the storage efficiency $\eta _{s}$. Table 2 compares the current configuration (first column) based on a 1 at.% constant doping gain medium (WP) with alternative solutions offered by gradient doped gain media. To obtain the values presented in the table, the $g_{0}<1.33\ {\rm cm}^{-1}$ ASE limitation was imposed and the crystal thickness was kept at 1 cm. By increasing the pump power, one can increase the stored energy density, while never exceeding a local gain above $1.33\ {\rm cm}^{-1}$, by choosing the appropriate doping distribution. Increasing the pump power above $9\ {\rm kW}\ {\rm cm}^{-2}$ does not significantly improve the stored energy density due to the imposed limitation ($g_{0}< 1.33\ {\rm cm}^{-1}$). The stored energy efficiency reaches a 62.7% optimum for $6\ {\rm kW}\ {\rm cm}^{-2}$ pump power and a crystal of 0.3–3.3 at.% linear doping distribution. The amount of stored energy can be significantly increased from 3.29 up to $4.78\ {\rm J}\ {\rm cm}^{-2}$ by increasing the pump power to $8\ {\rm kW}\ {\rm cm}^{-2}$ while keeping the 59.8% efficiency of the constant doped case. The doping gradient necessary for this case is only $g=1.1$ at.% ${\rm cm}^{-1}$, a value already achieved with HDC and easier to obtain than the 3 at.% ${\rm cm}^{-1}$ of the previous case. It should be kept in mind that any pump power increase is related to major investment in laser diodes. The thickness of the crystal could also be reduced, but such optimization would only make sense in order to achieve better cooling efficiency. Considering that the current low temperature cooling system is highly effective^{[4, 6]}, this optimization does not really seem useful.

6. Conclusion and outlook

A methodology to define the optimum doping ion volume distribution was derived in the context of the Lucia DPSSL room and low temperature active mirror amplifiers. After delimiting an optimum region whose boundaries are defined by minimum energy storage and maximum ASE-compatible gain considerations, the optimum point is selected considering the axial gain contrast. Minimizing this gain modulation will help in homogenizing the thermal load, therefore reducing the internal stresses and associated losses (like depolarization) the gain medium is submitted to Ref. [9].

This approach is valid for other DPSSL amplifier architectures like the DIPOLE^[10] and PEnELOPE^[11] projects, where pumping takes place from both sides through the coolant.