No CrossRef data available.
Article contents
On generating a random sequence
Published online by Cambridge University Press: 14 July 2016
Extract
Suppose there are k kinds of balls identical except for their colours. The number of balls of the ith colour is ri (i = 1, 2, ···, k) and 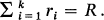 Put down the R balls in a sequence (a line), then an acceptable sequence is one which does not have two adjacent balls of the same colour. The problem is to generate a random sample of the set of acceptable sequences S(r 1, r 2, ···, rk ).
Put down the R balls in a sequence (a line), then an acceptable sequence is one which does not have two adjacent balls of the same colour. The problem is to generate a random sample of the set of acceptable sequences S(r 1, r 2, ···, rk ).
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1971
References
[2]
Mood, A. M. (1940) The distribution theory of runs. Ann. Math. Statist.
11, 367–392.Google Scholar

