Article contents
The progeny of a branching process
Published online by Cambridge University Press: 14 July 2016
Extract
1. Let {Z(t), t ≧ 0} be an age-dependent branching process with offspring generating function 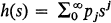 and life-time distribution function G(t). Denote by N(t) the progeny of the process, that is the total number of objects which have been born in [0, t], counting the ancestor. (See Section 2 for definitions.) Then in the Galton-Watson process (i.e., when G(t) = 0 for t ≦ 1, G(t) = 1 for t > 1) we have the simple relation Nn = Z 0 + Z 1 + ··· + Zn , so that the asymptotic behaviour of Nn as n → ∞ follows from a knowledge of the asymptotic behaviour of Zn . In particular, if 1 < m = h'(1) < ∞ and Zn (ω)/E(Zn ) → Z(ω) > 0 then also Nn (ω)/E(Nn ) → Z(ω) > 0; since E(Zn )/E(Nn ) → 1 – m –1 this means that
and life-time distribution function G(t). Denote by N(t) the progeny of the process, that is the total number of objects which have been born in [0, t], counting the ancestor. (See Section 2 for definitions.) Then in the Galton-Watson process (i.e., when G(t) = 0 for t ≦ 1, G(t) = 1 for t > 1) we have the simple relation Nn = Z 0 + Z 1 + ··· + Zn , so that the asymptotic behaviour of Nn as n → ∞ follows from a knowledge of the asymptotic behaviour of Zn . In particular, if 1 < m = h'(1) < ∞ and Zn (ω)/E(Zn ) → Z(ω) > 0 then also Nn (ω)/E(Nn ) → Z(ω) > 0; since E(Zn )/E(Nn ) → 1 – m –1 this means that
Information
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1971
References
- 6
- Cited by

