Article contents
Transient and slim versus recurrent and fat: Random walks and the trees they grow
Published online by Cambridge University Press: 01 October 2019
Abstract
The no restart random walk (NRRW) is a random network growth model driven by a random walk that builds the graph while moving on it, adding and connecting a new leaf node to the current position of the walker every s steps. We show a fundamental dichotomy in NRRW with respect to the parity of s: for 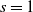 ${s}=1$ we prove that the random walk is transient and non-leaf nodes have degrees bounded above by an exponential distribution; for s even we prove that the random walk is recurrent and non-leaf nodes have degrees bounded below by a power law distribution. These theoretical findings highlight and confirm the diverse and rich behaviour of NRRW observed empirically.
${s}=1$ we prove that the random walk is transient and non-leaf nodes have degrees bounded above by an exponential distribution; for s even we prove that the random walk is recurrent and non-leaf nodes have degrees bounded below by a power law distribution. These theoretical findings highlight and confirm the diverse and rich behaviour of NRRW observed empirically.
MSC classification
Information
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2019
References
Amorim, B., Figueiredo, D., Iacobelli, G. and Neglia, G. (2016). Growing networks through random walks without restarts. In Complex Networks VII, eds Cherifi, H. et al., pp. 199–211. Springer.CrossRefGoogle Scholar
Angel, O., Crawford, N. and Kozma, G. (2014). Localization for linearly edge reinforced random walks. Duke Math. J
. 163, 889–921.CrossRefGoogle Scholar
Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.CrossRefGoogle ScholarPubMed
Campanino, M. and Petritis, D. (2014). Type transition of simple random walks on randomly directed regular lattices. J. Appl. Prob. 51, 1065–1080.CrossRefGoogle Scholar
Cannings, C. and Jordan, J. (2013). Random walk attachment graphs. Electron. Comm. Prob. 18, 1–5.CrossRefGoogle Scholar
Dembo, A., Huang, R. and Sidoravicius, V. (2014). Walking within growing domains: recurrence versus transience. Electron. J. Prob. 19, 1–20.CrossRefGoogle Scholar
Disertori, M., Sabot, C. and Tarrès, P. (2015). Transience of edge-reinforced random walk. Comm. Math. Phys. 339, 121–148.CrossRefGoogle Scholar
Figueiredo, D. R., Iacobelli, G., Oliveira, R. I., Reed, B. and Ribeiro, R. (2017). Building your path to escape from home. Available at arXiv:1709.10506.Google Scholar
Hoffman, C., Johnson, T. and Junge, M. (2016). From transience to recurrence with Poisson tree frogs. Ann. Appl. Prob. 26, 1620–1635.CrossRefGoogle Scholar
Ikeda, N. (2014). Network formed by movements of random walkers on a Bethe lattice. J. Phys. Conf. Series 490, 012189.CrossRefGoogle Scholar
Kumar, R., Novak, J. and Tomkins, A. (2010). Structure and evolution of online social networks. In Link Mining: Models, Algorithms, and Applications, eds Yu, P. S. et al., pp. 337–357. Springer.CrossRefGoogle Scholar
Li, M., Gao, L., Fan, Y., Wu, J. and Di, Z. (2010). Emergence of global preferential attachment from local interaction. New J. Phys
. 12, 043029.CrossRefGoogle Scholar
Saramäki, J. and Kaski, K. (2004). Scale-free networks generated by random walkers. Phys. A Stat. Mech. Appl. 341, 80–86.CrossRefGoogle Scholar
Vázquez, A. (2003). Growing network with local rules: preferential attachment, clustering hierarchy, and degree correlations. Phys. Rev. E 67, 056104.CrossRefGoogle ScholarPubMed
Weng, L., Ratkiewicz, J., Perra, N., Gonçalves, B., Castillo, C., Bonchi, F., Schifanella, R., Menczer, F. and Flammini, A. (2013). The role of information diffusion in the evolution of social networks. In ACM International Conference on Knowledge Discovery and Data Mining (KDD), pp. 356–364. ACM.CrossRefGoogle Scholar
- 3
- Cited by

