Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-30T21:55:28.340Z Has data issue: false hasContentIssue false
  • English
  • Français

On generating a random sequence

Published online by Cambridge University Press:  14 July 2016

F. K. Hwang  and
S. Lin
F. K. Hwang
Affiliation:
Bell Telephone Laboratories, Murray Hill, New Jersey
S. Lin
Affiliation:
Bell Telephone Laboratories, Murray Hill, New Jersey
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose there are k kinds of balls identical except for their colours. The number of balls of the ith colour is ri (i = 1, 2, ···, k) and 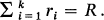Put down the R balls in a sequence (a line), then an acceptable sequence is one which does not have two adjacent balls of the same colour. The problem is to generate a random sample of the set of acceptable sequences S(r1, r2, ···, rk).

Type
Research Papers
Information
Journal of Applied Probability , Volume 8 , Issue 2 , June 1971 , pp. 366 - 373
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barton, D. E. and David, F. N. (1957) Multiple runs. Biometrika 44, 168–178.Google Scholar
[2] Mood, A. M. (1940) The distribution theory of runs. Ann. Math. Statist. 11, 367–392.Google Scholar