A selection of Bartlett's work as an operating statistician in his first position as statistician 1934–38 at the I.C.I. agricultural research station at Jealott's Hill, Berks., is described. This illustrates some of the methods he used for the efficient detection of treatment effects and for an appraisal of the suitability of the experimental designs that were being used.

Reciprocal pairs of continuous random variables on the line are considered, such that the density function of each is, to within a norming factor, the characteristic function of the other. The analogous reciprocal relationship between a discrete distribution on the line and a continuous distribution on the circle is also considered. A conjecture is made regarding infinite divisibility properties of such pairs of random variables. It is shown that the von Mises distribution is infinitely divisible for sufficiently small values of the concentration parameter.

The author determines the distribution and the limit distribution of the number of partial sums greater than k (k = 0, 1, 2, …) for n mutually independent and identically distributed discrete random variables taking on the integers 1, 0, − 1, − 2, ….

The conditional inference approach is shown to extend to the general regression problem and to give exact inferences for entirely arbitrary distributions.

Approximate parametric prediction intervals are obtained for an unobserved random variable when the amount of data on which to base the estimation is large. Applications include the construction of approximate confidence intervals in empirical Bayes estimation.

Bartlett and Williams have shown that the hypothesis of the goodness-of-fit of one or more assigned discriminant functions in the case of several groups can be tested using Wilks's A criterion. By factorizing this A criterion suitably, it is also possible to test whether the directions of the given functions are inadequate or whether the number of proposed functions is inadequate. Hotelling's statistic is a competitor of Wilks's A in multivariate analysis; previously its use for this hypothesis and also for the dimensionality and direction aspects of this hypothesis was unknown. The present paper derives the appropriate type statistics for this and also gives their exact null distributions.

The product-limit estimator for a distribution function, appropriate to observations which are variably censored, was introduced by Kaplan and Meier in 1958; it has provided a basis for study of more complex problems by Cox and by others. Its properties in the case of random censoring have been studied by Efron and later writers. The basic properties of the product-limit estimator are here shown to be closely parallel to the properties of the empirical distribution function in the general case of variably and arbitrarily censored observations.

The paper deals with two approaches to the estimation of the parameters β and σ2 in the General Gauss-Markoff (GGM) model represented by the triplet (Y, Xß, σ2V), where E(Y)=Xβ and D(Y) =σ2V, when no assumptions are made about the ranks of X and V. One is called Inverse Partition Matrix (IPM) method, which depends on the numerical evaluation of the g-inverse of a partitioned matrix. The second is an analogue of least squares theory applicable even when V is singular, unlike Atiken's method which is applicable only for non-singular V, and is called Unified Least Square (ULS) method.

The coefficient of correlation between suitably defined statistics provides a means of testing various parametric hypotheses. The distribution of such coefficients, when the null hypothesis is not true, takes various forms in different applications. In particular, the correlation coefficients used to test hypotheses about the structural parameters in linear functional relations have doubly non-central distributions.

For tests of correlation in some typical situations, the curvature of the function defining the power in terms of the parameter in the neighbourhood of the null hypothesis is determined. This curvature is shown to be simply related to that of the function defining the squared correlation coefficient in terms of the parameter, in the neighbourhood of its minimum.

The NIPALS approach is applied to the ‘soft’ type of model that has come to the fore in sociology and other social sciences in the last five or ten years, namely path models that involve latent variables which serve as proxies for blocks of directly observed variables. Such models are seen as hybrids of the ‘hard’ models of econometrics where all variables are directly observed (path models in the form of simultaneous equations systems) and the ‘soft’ models of psychology where the human mind is described in terms of latent variables and their directly observed indicators. For hybrid models that involve one or two latent variables the NIPALS approach has been developed in [38], [41] and [42]. The present paper extends the NIPALS approach to path models with three or more latent variables. Each new latent variable brings a rapid increase in the pluralism of possible model designs, and new problems arise in the parameter estimation of the models. Iterative procedures are given for the point estimation of the parameters. With a view to cases when the iterative estimation does not converge, a device of range estimation is developed, where high profile versus low profile estimates give ranges for the parameter estimates.

In this study some of the basic ideas needed for the application of the Wiener-Hopf Technique in solving problems occurring in applied probability theory are discussed; the paper aims to give a short introduction. The method is illustrated by applying it to two problems; one, although basic in probability theory, is rather simple to handle by this method. The second is much more intricate, but shows clearly the power of the method.

An exposition is given of the properties of the iterates of complex functions near a fixed point, with explicit expressions for their power series in certain cases. The relevance to problems in genetics and statistics is pointed out.

In the article below, we consider sets of non-random functions of time t admitting certain asymptotic distributions. Purely temporal and deterministic considerations lead us to associate to a set 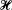, say, of functions H(t) of this type, a space Ω of samples ω.

To each function H(t) ⊂ 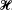, there corresponds a random variable h (ω). To the set of translated functions H(t + λ) of a function H(t) ⊂ 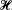, there corresponds a stationary random function of the translation parameter λ, say, h(λ, ω). We study the transposition to the set 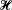of non-random functions H(t) of such properties as moments, gaussian character, independence, harmonic analysis, and others, of the random variables h (ω) and of the random functions h (λ, ω).

Some remarks are made concerning the links between ergodicity and the above problems.

This note deals with a q-dimensional stochastic vector process x(t) = {x1 (t), …, xq (t)}, satisfying certain stated general conditions. For such a process, there is a representation (1) in terms of stochastic innovations acting throughout the past of the process. The number N of terms in this representation is called the multiplicity of the x(t) process, and is uniquely determined by the process. For a one-dimensional process (q = 1) it is known that under certain conditions we have N = 1. For an arbitrary value of q, this note gives conditions under which we have N ≦ q.

Recent work by Moussouris [10] has clarified our present knowledge of finite Markov fields. The present note examines, in a loose and general fashion, whether one can extend the treatment to infinite fields.

An anticipation process is a continuous-time Markov process, having an element of deterministic drift in its transition structure. The theory of such processes, developed here from an elementary (Chapman-Kolmogorov) point of view, draws together a number of threads of theoretical and applied probability.

It is well-known that the transition matrix of a reversible Markov process can have only real eigenvalues. An example is constructed which shows that the converse assertion does not hold. A generalised notion of reversibility is proposed, ‘dynamic reversibility’, which has many of the implications for the form of the transition matrix of the classical definition, but which does not exclude ‘circulation in state-space’ or, indeed, periodicity.

The problem considered is that of measuring the velocity of a signal, constituted by a plane wave, from measurements at a number of recorders receiving noise as well as signal. The asymptotic properties of the estimates are considered under rather general conditions on the noise and signal processes.

This paper is an attempt to interpret and extend, in a more statistical setting, techniques developed by D. L. Snyder and others for estimation and filtering for doubly stochastic point processes. The approach is similar to the Kalman-Bucy approach in that the updating algorithms can be derived from a Bayesian argument, and lead ultimately to equations which are similar to those occurring in stochastic approximation theory. In this paper the estimates are derived from a general updating formula valid for any point process. It is shown that almost identical formulae arise from updating the maximum likelihood estimates, and on this basis it is suggested that in practical situations the sequence of estimates will be consistent and asymptotically efficient. Specific algorithms are derived for estimating the parameters in a doubly stochastic process in which the rate alternates between two levels.