Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-11T00:20:44.817Z Has data issue: false hasContentIssue false
  • English
  • Français

Breakdown of the Bretherton law due to wall slippage

Published online by Cambridge University Press:  07 February 2014

Yen-Ching Li ,
Ying-Chih Liao ,
Ten-Chin Wen  and
Hsien-Hung Wei
Yen-Ching Li
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
Ying-Chih Liao
Affiliation:
Department of Chemical Engineering, National Taiwan University, Taipei 10617, Taiwan
Ten-Chin Wen
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
Hsien-Hung Wei*
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
*
†Email address for correspondence: hhwei@mail.ncku.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

Against the common wisdom that wall slip plays only a minor role in global flow characteristics, here we demonstrate theoretically for the displacement of a long bubble in a slippery channel that the well-known Bretherton 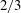$2/3$ law can break down due to a fraction of wall slip with the slip length 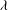$\lambda $ much smaller than the channel depth 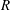$R$. This breakdown occurs when the film thickness 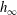$h_{\infty } $ is smaller than 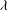$\lambda $, corresponding to the capillary number 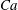$Ca$ below the critical value 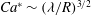$Ca^{\ast } \sim (\lambda /R)^{3 / 2}$. In this strong slip regime, a new quadratic law 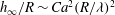$h_{\infty } /R \sim Ca^{2} (R/\lambda )^{2}$ is derived for a film much thinner than that predicted by the Bretherton law. Moreover, both the 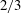$2/3$ and the quadratic laws can be unified into the effective 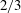$2/3$ law, with the viscosity 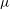$\mu $ replaced by an apparent viscosity 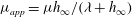$\mu _{app}= \mu h_{\infty } /({\lambda } + h_{\infty })$. A similar extension can also be made for coating over textured surfaces where apparent slip lengths are large. Further insights can be gained by making a connection with drop spreading. We find that the new quadratic law can lead to 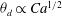$\theta _{d} \propto Ca^{1 / 2} $ for the apparent dynamic contact angle of a spreading droplet, subsequently making the spreading radius grow with time as 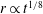$r \propto t^{1 / 8}$. In addition, the precursor film is found to possess 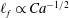$\ell _{f} \propto Ca^{ - 1 / 2}$ in length and therefore spreads as 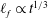$\ell _{f} \propto t^{1 / 3}$ in an anomalous diffusion manner. All these features are accompanied by no-slip-to-slip transitions sensitive to the amount of slip, markedly different from those on no-slip surfaces. Our findings not only provide plausible accounts for some apparent departures from no-slip predictions seen in experiments, but also offer feasible alternatives for assessing wall slip effects experimentally.

JFM classification

Materials Processing Flows: Coating Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , pp. 200 - 227
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajdari, A. & Bocquet, L. 2006 Giant amplification of interfacially driven transport by hydrodynamic slip: diffusio-osmosis and beyond. Phys. Rev. Lett. 96, 186102.CrossRefGoogle ScholarPubMed
Albrecht, U., Otto, A. & Leiderer, P. 1992 Two-dimensional liquid polymer diffusion: experiment and simulation. Phys. Rev. Lett. 68, 3192–3195.Google Scholar
Asmolov, E. S. & Vinogradova, O. I. 2012 Effective slip boundary conditions for arbitrary one-dimensional surfaces. J. Fluid Mech. 706, 108–117.Google Scholar
Beavers, G. S. & Joseph, D. D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207.Google Scholar
Belyaev, A. V. & Vinogradova, O. I. 2010 Effective slip in pressure-driven flow past super-hydrophobic stripes. J. Fluid Mech. 652, 489–499.CrossRefGoogle Scholar
Bico, J. & Quéré, D. 2002 Self-propelling slugs. J. Fluid Mech. 467, 101–127.CrossRefGoogle Scholar
Bocquet, L. & Barrat, J. L. 2007 Flow boundary conditions from nano- to micro-scales. Soft Matt. 3, 685–693.CrossRefGoogle ScholarPubMed
Bonaccurso, E., Butt, H.-J. & Craig, V. S. J. 2003 Surface roughness and hydrodynamic boundary slip of a Newtonian fluid in a completely wetting system. Phys. Rev. Lett. 90, 144501.CrossRefGoogle Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.Google Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188.Google Scholar
Brochard, F. & de Gennes, P. G. 1984 Spreading laws for liquid polymer droplets: interpretation of the foot. J. Phys. Lett. 45, 597–602.Google Scholar
Brochard-Wyart, F., de Gennes, P. G., Hervert, H. & Redon, C. 1994 Wetting and slippage of polymer melts on semi-ideal surfaces. Langmuir 10, 1566–1572.Google Scholar
Brochard-Wyart, F., Debrégeas, G. & de Gennes, P. G. 1996 Spreading of viscous droplets on a non viscous liquid. Colloid Polym. Sci. 274, 70–72.CrossRefGoogle Scholar
Cassie, A. B. D. & Baxter, S. 1944 Wettability of porous surfaces. Trans. Faraday Soc. 40, 546–551.Google Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.Google Scholar
Chen, J.-D. 1988 Experiments on a spreading drop and its contact angle on a solid. J. Colloid Interface Sci. 122, 60–72.CrossRefGoogle Scholar
Choi, C.-H. & Kim, C.-J. 2006 Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys. Rev. Lett. 96, 066001.CrossRefGoogle Scholar
Choi, C.-H., Ulmanella, U., Kim, J., Ho, C.-M. & Kim, C.-J. 2006 Effective slip and friction reduction in nanograted superhydrophobic microchannels. Phys. Fluids 18, 087105.Google Scholar
Choi, C.-H., Westin, K. J. A. & Breuer, K. S. 2003 Apparent slip flows in hydrophilic and hydrophobic microchannels. Phys. Fluids 15, 2897–2902.Google Scholar
Craig, V. S. J., Neto, C. & Williams, D. R. M. 2001 Shear-dependent boundary slip in an aqueous Newtonian liquid. Phys. Rev. Lett. 87, 054504.CrossRefGoogle Scholar
Denkov, N. D., Subramanian, V., Gurovich, D. & Lips, A. 2005 Wall slip and viscous dissipation in sheared foams: effect of surface mobility. Colloids Surf. A 263, 129–145.Google Scholar
Devauchelle, O., Josserand, C. & Zaleski, S. 2007 Forced dewetting on porous media. J. Fluid Mech. 574, 343–364.Google Scholar
Eggers, J. 2004 Toward a description of contact line motion at higher capillary numbers. Phys. Fluids 16, 3491–3494.CrossRefGoogle Scholar
Eggers, J. & Stone, H. A. 2004 Characteristic lengths at moving contact lines for a perfectly wetting fluid: the influence of speed on the dynamic contact angle. J. Fluid Mech. 505, 309–321.CrossRefGoogle Scholar
Feuillebois, F., Bazant, M. Z. & Vinogradova, O. I. 2009 Effective slip over superhydrophobic surfaces in thin channels. Phys. Rev. Lett. 102, 026001.Google Scholar
de Gennes, P. G. 1979 Ecoulements viscométriques de polymères enchevêtrés. C. R. Acad. Sci. Paris B 288, 219–220.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.Google Scholar
de Gennes, P. G., Brochard-Wyart, F. & Quéré, D. 2003 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Hervet, H. & de Gennes, P. G. 1984 Dynamique du mouillage: films précurseurs sur solides ‘sec’. C. R. Acad. Sci. Paris II 299, 499–503.Google Scholar
Heslot, F., Cazabat, A. M. & Levinson, P. 1989 Dynamics of wetting of tiny drops: ellipsometric study of the late stages of spreading. Phys. Rev. Lett. 62, 1286–1289.Google Scholar
Hocking, L. M. 1976 A moving fluid interface. Part 2. The removal of the force singularity by a slip flow. J. Fluid Mech. 79, 209–229.Google Scholar
Hoffman, R. L. 1975 A study of the advancing interface. Part 1. Interface shape in liquid–gas systems. J. Colloid Interface Sci. 50, 228–241.Google Scholar
Kalliadasis, S. & Chang, H.-C. 1994 Apparent dynamic contact angle of an advancing gas–liquid meniscus. Phys. Fluids 6, 12–23.Google Scholar
Kalliadasis, S. & Chang, H.-C. 1996 Dynamics of liquid spreading on solid surfaces. Ind. Engng Chem. Res. 35, 2860–2874.CrossRefGoogle Scholar
Krechetnikov, R. & Homsy, G. M. 2005 Experimental study of substrate roughness and surfactant effects on the Landau–Levich law. Phys. Fluids 17, 102108.Google Scholar
Landau, L. & Levich, B. 1942 Dragging of a liquid by a moving plate. Acta Physicochim. USSR 17, 42–54.Google Scholar
Lauga, E., Brenner, M. & Stone, H. 2007 Microfluidics: the no-slip boundary condition. In Springer Handbook of Experimental Fluid Mechanics pp. 1219–1240. Springer.Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.Google Scholar
Liao, Y.-C., Li, Y.-C. & Wei, H.-H. 2013 Drastic changes in interfacial hydrodynamics due to wall slippage: slip-intensified film thinning, drop spreading, and capillary instability. Phys. Rev. Lett. 111, 136001.CrossRefGoogle ScholarPubMed
Lopez, J., Miller, C. A. & Ruckenstein, E. 1976 Spreading kinetics of liquid drops on solids. J. Colloid Interface Sci. 56, 460–468.CrossRefGoogle Scholar
Mate, C. M. 2012 Anomalous diffusion kinetics of the precursor film that spreads from polymer droplets. Langmuir 28, 16821–16827.Google Scholar
Navier, C. L. M. H. 1823 Mémoire sur les lois du mouvement des fluides. Mem. Acad. Sci. Inst. Fr. 6, 389–440.Google Scholar
Oskooei, S. A. K. & Sinton, D. 2010 Partial wetting gas–liquid segmented flow microreactor. Lab on a Chip 10, 1732–1734.Google Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38, 71–99.Google Scholar
Ratulowski, J. & Chang, H.-C. 1989 Transport of gas bubbles in capillaries. Phys. Fluids A 1, 1642–1655.CrossRefGoogle Scholar
Reinelt, D. A. & Saffman, P. G. 1985 The penetration of a finger into a viscous fluid in a channel and tube. SIAM J. Sci. Stat. Comput. 6, 542–561.Google Scholar
Restagno, F., Crassous, J., Charlaix, É., Cottin-Bizonne, C. & Monchanin, M. 2002 A new surface forces apparatus for nanorheology. Rev. Sci. Instrum. 73, 2292–2297.Google Scholar
Saugey, A., Drenckhan, W. & Weaire, D. 2006 Wall slip of bubbles in foams. Phys. Fluids 18, 053101.Google Scholar
Savva, N. & Kalliadasis, S. 2011 Dynamics of moving contact lines: a comparison between slip and precursor film models. Europhys. Lett. 94, 64004.CrossRefGoogle Scholar
Sbragaglia, M, Benzi, R., Biferale, L., Succi, S. & Toschi, F. 2006 Surface roughness–hydrophobicity coupling in microchannel and nanochannel flows. Phys. Rev. Lett. 97, 204503.Google Scholar
Seiwert, J., Clanet, C. & Quéré, D. 2011 Coating of a textured solid. J. Fluid Mech. 669, 55–63.CrossRefGoogle Scholar
Shirtcliffe, N. J., McHale, G., Atherton, S. & Newton, M. I. 2010 An introduction to superhydrophobicity. Adv. Colloid Interface Sci. 161, 124–138.Google Scholar
Song, H., Tice, J. D. & Ismagilov, R. F. 2003 A microfluidic system for controlling reaction networks in time. Angew. Chem. Intl Ed. Engl. 42, 768–772.Google Scholar
Stone, H. A. 2010 Interfaces: in fluid mechanics and across disciplines. J. Fluid Mech. 645, 1–25.Google Scholar
Tanner, L. H. 1979 The spreading of silicone oil drops on horizontal surfaces. J. Phys. D 12, 1473–1484.Google Scholar
Teletzke, G. F., Davis, H. D. & Scriven, L. E. 1988 Wetting hydrodynamics. Rev. Phys. Appl. (Paris) 23, 989–1007.Google Scholar
Tretheway, D. C. & Meinhart, C. D. 2002 Apparent fluid slip at hydrophobic microchannel walls. Phys. Fluids 14, L9–L12.Google Scholar
Tsai, P., Peters, A. M., Pirat, C., Wessling, M., Lammertink, R. G. H. & Loshe, D. 2009 Quantifying effective slip length over micropatterned hydrophobic surfaces. Phys. Fluids 21, 112002.Google Scholar
Tyrrell, J. W. G. & Attard, P. 2001 Images of nanobubbles on hydrophobic surfaces and their interactions. Phys. Rev. Lett. 87, 176104.Google Scholar
Vinogradova, O. I. 1995 Drainage of a thin liquid film confined between hydrophobic surfaces. Langmuir 11, 2213–2220.Google Scholar
Wenzel, R. N. 1936 Resistance of solid surfaces to wetting by water. Ind. Engng Chem. 28, 988–994.Google Scholar
Xu, H., Shirvanyants, D., Beers, K., Matyjaszewski, K., Rubinstein, M. & Sheiko, S. S. 2004 Molecular motion in a spreading precursor film. Phys. Rev. Lett. 93, 206103.Google Scholar
Ybert, C., Barentin, C., Cottin-Bizonne, C., Joseph, P. & Bocquet, L. 2007 Achieving large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19, 123601.Google Scholar
Yeo, L. Y. & Chang, H.-C. 2006 Electrowetting films on parallel line electrodes. Phys. Rev. E E 73, 011605.Google Scholar
Zhu, Y. & Granick, S. 2001 Rate-dependent slip of Newtonian liquid at smooth surfaces. Phys. Rev. Lett. 87, 096105.Google Scholar