Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T06:34:51.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Droplet–turbulence interaction in a confined polydispersed spray: effect of droplet size and flow length scales on spatial droplet–gas velocity correlations

Published online by Cambridge University Press:  07 February 2014

S. Sahu ,
Y. Hardalupas  and
A. M. K. P. Taylor
S. Sahu*
Affiliation:
Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK
Y. Hardalupas
Affiliation:
Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK
A. M. K. P. Taylor
Affiliation:
Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK
*
†Present address: Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India. Email address for correspondence: ssahu@iitm.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper discusses the interaction between droplets and entrained turbulent air flow in the far-downstream locations of a confined polydispersed isothermal spray. Simultaneous and planar measurements of droplet and gas velocities in the spray along with droplet size are obtained with the application of a novel experimental technique, developed by Hardalupas et al. (Exp. Fluids, vol. 49, 2010, pp. 417–434), which combines interferometric laser imaging for droplet sizing (ILIDS) with particle image velocimetry (PIV). These measurements quantified the spatial correlation coefficients of droplet–gas velocity fluctuations (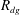$R_{dg}$) and droplet–droplet velocity fluctuations (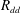$R_{dd}$) conditional on droplet size classes, for various separation distances, and for axial and cross-stream velocity components. At the measurement location close to the spray edge, with increasing droplet size, 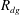$R_{dg}$ was found to increase in axial direction and decrease in cross-stream direction. This suggests that as the gas-phase turbulence becomes more anisotropic away from the spray axis, the gravitational influence on droplet–gas correlated motion tends to increase. The effective length scales of the correlated droplet–gas motion were evaluated and compared with that for gas and droplet motion. The role of different turbulent eddies of the gas flow on the droplet–gas interaction was examined. The flow structures were extracted using proper orthogonal decomposition (POD) of the instantaneous gas velocity data, and their contribution on the spatial droplet–gas velocity correlation was evaluated, which quantified the momentum transfer between the two phases at different length scales of the gas flow. The droplets were observed to augment turbulence for the first three POD modes (larger scales) and attenuate it for the rest of the modes (smaller scales). It has been realized that apart from droplet Stokes number and mass loading, the dynamic range of length scales of the gas flow and the relative turbulent kinetic energy content of the flow structures (POD modes) must be considered in order to conclude if the droplets enhance or reduce the carrier-phase turbulence especially at the lower wavenumbers.

JFM classification

Drops and Bubbles: Drops and Bubbles Nonlinear Dynamical Systems: Low-dimensional models Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , pp. 98 - 138
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Aubry, N. 1991 On the hidden beauty of the proper orthogonal decomposition. Theor. Comput. Fluid Dyn. 2, 339–352.Google Scholar
Ayyalasomayajula, S., Gylfason, A., Collins, L. R., Bodenschatz, E. & Warhaft, Z. 2006 Lagrangian measurements of inertial particle accelerations in grid generated wind tunnel turbulence. Phys. Rev. Lett. 97, 144507.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flows. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A., Msacchio, S. & Toschi, F. 2006 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 550, 349–358.Google Scholar
Boivin, M., Simonin, O. & Squires, K. 1998 Direct numerical simulation of turbulence modulation by particles in isotropic turbulence. J. Fluid Mech. 375, 235–263.Google Scholar
Boree, J., Ishima, T. & Flour, I. 2001 The effect of mass loading and inter-particle collisions on the development of the polydispersed two-phase flow downstream of a confined bluff body. J. Fluid Mech. 443, 129–165.Google Scholar
Borowsky, J. F. & Wei, T. 2011 Two-phase interactions through turbulent events as described by fluidparticle correlations. Chem. Engng Sci. 66, 128–134.Google Scholar
Chen, C. P. & Wood, P. E. 1985 A turbulence closure model for dilute gas–particle flows. Can. J. Chem. Engng 65, 349–360.Google Scholar
Chien, R. & Chung, J. N. 1987 Effects of vortex pairing on particle-dispersion in turbulent shear flows. Intl J. Multiphase Flow 13, 785–802.Google Scholar
Crowe, C. T., Gore, R. A. & Troutt, T. R. 1985 Particle dispersion by coherent structures in free shear flows. Part. Science Technol. 3, 149–158.Google Scholar
Crowe, C., Sommerfield, M. & Tsuji, Y. 1998 Multiphase Flows with Droplets and Particles. CRC Press.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52, 309–329.Google Scholar
Elghobashi, S. & Abou-Arab, T. W. 1983 A two-equation turbulence model for two-phase flows. Phys. Fluids 26, 931–938.Google Scholar
Ferrand, V., Bazile, R, Boree, J. & Charnay, G. 2003 Gas-droplet turbulent velocity correlations and two-phase interaction in an axisymmetric jet laden with partly responsive droplets. Intl J. Multiphase Flow 29, 195–217.CrossRefGoogle Scholar
Ferrante, A. & Elghobashi, S. 2003 On the physical mechanism of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 15, 315–329.Google Scholar
Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in turbulent channel flow. Phys. Fluids 6, 3742–3749.Google Scholar
Fevrier, P., Simonin, O. & Squires, K. 2005 Partitioning of particle velocities in gas–solid turbulent flows into a continuous field and a spatially uncorrelated random distribution: theoretical formalism and numerical study. J. Fluid Mech. 533, 1–46.Google Scholar
Geiss, S., Dreizler, A., Stojanovic, Z., Chrigui, M., Sadiki, A. & Janicka, J. 2004 Investigation of turbulence modification in a non-reactive two-phase flow. Exp. Fluids 36, 344–354.Google Scholar
Glover, A. R., Skippon, S. M. & Boyle, R. D. 1995 Interferometric laser imaging for droplet sizing: a method for droplet-size measurement in sparse spray systems. Appl. Optics 34, 8409–8421.Google Scholar
Gui, L., Wereley, S. T. & Kim, Y. H. 2003 Advances and applications of the digital mask technique in particle image velocimetry experiments. Meas. Sci. Technol. 14, 1820–1828.Google Scholar
Hardalupas, Y. & Horender, S. 2003 A method to estimate gas–droplet velocity cross correlations in sprays. Atomiz. Sprays 13, 273–295.Google Scholar
Hardalupas, Y. & Horender, S 2010 Fluid particle correlated motion and turbulent energy transfer in a two-dimensional particle-laden shear flow. Chem. Engng Sci. 65, 5075–5091.Google Scholar
Hardalupas, Y., Sahu, S., Taylor, A. M.K. P. & Zarogoulidis, K. 2010 Simultaneous planar measurement of droplet velocity and size with gas phase velocities in a spray by combined ILIDS and PIV techniques. Exp. Fluids 49, 417–434.Google Scholar
Hardalupas, Y., Taylor, A. M. K. P. & Whitelaw, J. H. 1989 Velocity and particle-flux characteristics of turbulent particle-laden jets. Proc. R. Soc. Lond. 426 (1870), 31–78.Google Scholar
Hardalupas, Y., Taylor, A. M. K. P. & Whitelaw, J. H. 1990 Velocity and size characteristics of liquid-fuelled flames stabilized by a swirl burner. Proc. R. Soc. Lond. 428 (1874), 129–155.Google Scholar
Hardalupas, Y., Taylor, A. M. K. P. & Whitelaw, J. H. 1992 Particle dispersion in a vertical round sudden-expansion flow. Proc. R. Soc. Lond. 411–442.Google Scholar
Hwang, W. & Eaton, J. K. 2006 Homogeneous and isotropic turbulence modulation by small heavy (ST 50) particles. J. Fluid Mech. 564, 361–393.Google Scholar
Jong, J., Cao, L., Woodward, S., Salazar, J., Collins, L. & Meng, H. 2009 Dissipation rate estimation from PIV in zero-mean isotropic turbulence. Exp. Fluids 46, 499–515.Google Scholar
Kavounides, C.2006 Particle flows in spray dryers. PhD thesis, Imperial College London.Google Scholar
Kawaguchi, T., Akasaka, Y. & Maeda, M. 2002 Size measurements of droplets and bubbles by advanced interferometric laser imaging technique. Meas. Sci. Technol. 13, 308–316.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2003 Effect of particle size on velocity correlations in turbulent channel flow. In Proceedings of the 4th ASME–JSME Joint Fluids Engineering Conference, Honolulu, Hawaii, FEDSM03-45730 .Google Scholar
Kiger, K. T. & Pan, C. 2002 Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow. J. Turbul. 3, 1–21.Google Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 277, 109–134.Google Scholar
Lazaro, B. J. & Lasheras, J. C. 1992 Particle dispersion in the developing free shear layer. Part 1 unforced flow. Part 2 forced flow. J. Fluid Mech. 235, 143–221.Google Scholar
Li, F., Qi, H. & You, C. 2010 Phase doppler anemometry measurements and analysis of turbulence modulation in dilute gas–solid two-phase shear flows. J. Fluid Mech. 663, 434–455.Google Scholar
Longmire, E. K. & Eaton, J. K. 1992 Structure of a particle-laden round jet. J. Fluid Mech. 236, 217–257.Google Scholar
Lumley, J. L.1967 The structure of inhomogeneous turbulent flows. In Proceedings of the International Colloqium on the Fine Scale Structure of the Atmosphere and its Influence on Radio Wave Propagation.Google Scholar
Maeda, M., Kawaguchi, T. & Hishida, K. 2000 Novel interferometric measurement of size and velocity distributions of spherical particles in fluid flows. Meas. Sci. Technol. 11, 13–18.Google Scholar
Mashayek, F. & Taulbee, D. B. 2002 Turbulent gas–solid flows. Part II: explicit algebraic closures. Numer. Heat Transfer, Part B 41, 31–52.Google Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2012 Analyzing preferential concentration and clustering of inertial particles in turbulence. Intl J. Multiphase Flow 40, 1–18.Google Scholar
Okamoto, K., Nishio, S., Saga, T. & Kobayashi, T. 2000 Standard images for particle-image velocimetry. Meas. Sci. Technol. 11, 685–691.Google Scholar
Poelma, C., Westerweel, J. & Ooms, G. 2007 Particle–fluid interaction in grid-generated turbulence. J. Fluid Mech. 589, 315–351.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prasad, A. K. & Jensen, K. 1995 Scheimpflug stereocamera for particle image velocimetry in liquid flows. Appl. Optics 34, 7092–7099.Google Scholar
Prevost, F., Boree, J., Nuclisch, H. J. & Charnay, G. 1996 Measurements of fluid/particle correlated motion in the far field of an axisymmetric jet. Intl J. Multiphase Flow 22, 685–701.Google Scholar
Reeks, M. W. 1977 On the dispersion of small particles suspended in an isotropic turbulent fluid. J. Fluid Mech. 83, 529–546.Google Scholar
Risso, F. & Fabre, J. 1997 Diffusive turbulence in a confined jet experiment. J. Fluid Mech. 337, 233–261.Google Scholar
Ronneberger, O., Raffel, M. & Kompenhans, J. 1998 Advanced evaluation algorithms for standard and dual plane particle image velocimetry. In Proceedings of the 9th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, p. 10.1.Google Scholar
Sahu, S.2011 Experimental study of isothermal and evapourative sprays. PhD thesis, Imperial College London.Google Scholar
Sakakibara, J., Wicker, R. B. & Eaton, J. K. 1996 Measurements of the particle–fluid velocity correlation and the extra dissipation in a round jet. Intl J. Multiphase Flow 22, 863–881.Google Scholar
Simonin, O., Deutsch, E. & Minier, J. P. 1993 Eulerian prediction of the fluid/particle correlated motion in turbulent two-phase flows. Appl. Sci. Res. 51, 275–283.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures, Part I, II, III. Q. Appl. Maths 45, 560–590.Google Scholar
Squires, K. & Eaton, J. 1990 Particle response and turbulence modification in isotropic turbulence. Phys. Fluids 7, 1191–1203.Google Scholar
Sundaram, S. & Collins, L. 1999 A numerical study of the modulation of isotropic turbulence by suspended particles. J. Fluid Mech. 379, 105–143.Google Scholar
Tanaka, T. & Eaton, J. 2010 Sub-Kolmogorov resolution partical image velocimetry measurements of particle-laden forced turbulence. J. Fluid Mech. 643, 177–206.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Tsuji, Y., Morikawa, Y. & Shiomi, H. H. 1984 LDV measurements of an air–solid two-phase flow in a vertical pipe. J. Fluid Mech. 139, 417–434.Google Scholar
Vance, M. W., Squires, K. D. & Simonin, O. 2006 Properties of the particle velocity field in gas–solid turbulent channel flow. Phys. Fluids 18, 063302.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Wood, A. M., Hwang, W. & Eaton, J. K. 2005 Preferential concentration of particles in homogeneous and isotropic turbulence. Intl J. Multiphase Flow 31, 1220–1230.Google Scholar
Yang, C. Y. & Le, I. U. 1998 The role of the turbulent scales on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 371, 179–205.Google Scholar
Yang, T. S. & Shy, S. S. 2005 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 526, 171–216.Google Scholar
Zimmer, L., Domann, R., Hardalupas, Y. & Ikeda, Y. 2003 Simultaneous laser induced fluorescence and Mie scattering for droplet cluster measurements. AIAA J. 41, 2170–2178.Google Scholar