Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T00:39:41.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Detailed force modelling of the secondary load cycle

Published online by Cambridge University Press:  21 February 2020

Amin Ghadirian Open the ORCID record for Amin Ghadirian [Opens in a new window]  and
Henrik Bredmose Open the ORCID record for Henrik Bredmose [Opens in a new window]
Amin Ghadirian*
Affiliation:
DTU Wind Energy, Nils Koppels Allé, Building 403, DK-2800Kgs. Lyngby, Denmark
Henrik Bredmose
Affiliation:
DTU Wind Energy, Nils Koppels Allé, Building 403, DK-2800Kgs. Lyngby, Denmark
*
†Email address for correspondence: amgh@dtu.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

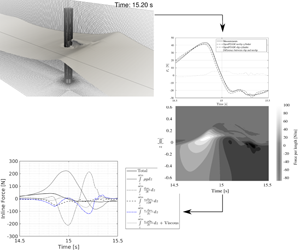
Steep wave passage around vertical circular cylinders is associated with an additional force peak occurring after the main peak: the secondary load cycle. The secondary load cycle for a focused wave group typical of offshore wind turbine foundations at 33 m full-scale water depth is investigated in scale 1 : 50. Ensemble-averaged force, front face pressures and free surface elevation measurements are used as the basis for the investigation. A two-phase free-surface Reynolds-averaged Navier–Stokes solver is validated against generic cases of turbulent flow over a wall, wave-boundary layer flow for a Reynolds number, $Re$, of $1\times 10^{4}<Re<1\times 10^{7}$, two-dimensional (2-D) drag on a cylinder for $1\times 10^{2}<Re<2.5\times 10^{5}$ and 2-D oscillatory flow for three combinations of $Re=\{5.8\times 10^{4},9\times 10^{4},1.7\times 10^{5}\}$ and Keulegan–Carpenter number, $KC=\{6,12,18\}$, respectively. The solver is next applied to reproduce ensemble-averaged experimental results of the focused wave group and a good match for the inline force and free surface elevation is found along with a good match for the measured front face pressures. The numerical solution for the focused wave is next analysed in detail to explain the cause of the secondary load cycle. We find that the secondary load cycle is confined to an upper region ranging from just above the still water level to 1.5 cylinder diameters below. By a further break down of the pressure field into contributions from the individual terms of the vertical Navier–Stokes equation, we find that the local force peak in the secondary load cycle is mainly caused by suction effects around the still water level on the back side, contributed through the material time derivative of the vertical velocity, $\text{D}\unicode[STIX]{x1D70C}u_{z}/\text{D}t$. The suction occurs due to the rapid decrease of water level below the generated water column at the back of the cylinder, which at this time has only just begun its downward motion. The first force local minimum in the secondary load cycle is aided by the hydrostatic pressure from the water column while the second local minimum of the secondary load cycle is aided by wash-down effects on the front side. Finally, the role of the observed vortices behind the cylinder is discussed and compared to reference computations with slip conditions. The results confirm findings from earlier slip boundary studies that the global force history through the secondary load cycle is not strongly affected by the boundary layer. The source of vortices behind the cylinder, observed in both sets of computations is discussed.

JFM classification

Geophysical and Geological Flows: Coastal engineering Waves/Free-surface Flows: Wave scattering
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 889 , 25 April 2020 , A21
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bredmose, H., Dixen, M., Ghadirian, A., Larsen, T., Schløer, S., Andersen, S. J., Wang, S., Bingham, H. B., Lindberg, O., Christensen, E. D. et al. 2016 DeRisk – Accurate prediction of ULS wave loads. Outlook and first results. Energy Procedia 94, 379–387.CrossRefGoogle Scholar
Bredmose, H., Hunt-Raby, A., Jayaratne, R. & Bullock, G. N. 2010 The ideal flip-through impact: experimental and numerical investigation. J. Engng Maths 67 (1), 115–136.CrossRefGoogle Scholar
Brown, S., Magar, V., Greaves, D. M. & Conley, D. C. 2014 An evaluation of RANS turbulence closure models for spilling breakers. Coast. Engng Proc. 1 (34), 1–5.Google Scholar
Chaplin, J. R., Rainey, R. C. T. & Yemm, R. W. 1997 Ringing of a vertical cylinder in waves. J. Fluid Mech. 350, 119–147.CrossRefGoogle Scholar
Dean, R. & Dalrymple, R. A. 1991 Water Wave Mechanics for Engineers and Scientists. World Scientific.CrossRefGoogle Scholar
Deshpande, S. S., Anumolu, L. & Trujillo, M. F. 2012 Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Disc. 5 (1), 014016.CrossRefGoogle Scholar
Devolder, B., Rauwoens, P. & Troch, P. 2017 Application of a buoyancy-modified k–𝜔 SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM®. Coast. Engnng 125 (June 2016), 81–94.CrossRefGoogle Scholar
Eltard, B., Fuhrman, D. R. & Roenby, J.2017 Performance of interFoam on the simulation of progressive waves. arXiv:1804.01158.Google Scholar
Engsig-Karup, A. P., Bingham, H. B. & Lindberg, O. 2009 An efficient flexible-order model for 3D nonlinear water waves. J. Comput. Phys. 228 (6), 2100–2118.CrossRefGoogle Scholar
Fredsøe, J., Sumer, B. M., Kozakiewicz, A., Chua, L. H. & Deigaard, R. 2003 Effect of externally generated turbulence on wave boundary layer. Coast. Engng 49 (3), 155–183.CrossRefGoogle Scholar
Ghadirian, A., Bredmose, H. & Dixen, M. 2016 Breaking phase focused wave group loads on offshore wind turbine monopiles. J. Phys.: Conf. Ser. 753 (9), 092004.Google Scholar
Ghadirian, A., Bredmose, H. & Schløer, S. 2017 Prediction of the shape of inline wave force and free surface elevation using First Order Reliability Method (FORM). Energy Procedia 137 (January), 162–176.CrossRefGoogle Scholar
Goda, Y. & Suzuki, Y. 1976 Estimation of incident and reflected waves in random wave experiments. In Proceedings of the 15th International Conference on Coastal Engineering, ASCE, pp. 828–845.Google Scholar
Greenshields, C. J.2015 OpenFOAM-3.0.1 (December).Google Scholar
Grue, J. 2002 On four highly nonlinear phenomena in wave theory and marine hydrodynamics. Appl. Ocean Res. 24 (5), 261–274.CrossRefGoogle Scholar
Grue, J., Bjørshol, G. & Strand, Ø. 1994 Nonlinear wave loads which may generate ‘Ringing’ responses of offshore structure. In Workshop on Water Waves and Floating Bodies.Google Scholar
Grue, J. & Huseby, M. 2002 Higher harmonic wave forces and ringing of vertical cylinders. Appl. Ocean Res. 24 (4), 203–214.CrossRefGoogle Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39 (1), 201–225.CrossRefGoogle Scholar
Jacobsen, N. G.2011 A full hydro- and morphodynamic description of breaker bar development. PhD thesis.CrossRefGoogle Scholar
Jacobsen, N. G.2017 waves2Foam Manual. Tech. Rep. August. Deltares.Google Scholar
Jacobsen, N. G., Fuhrman, D. R. & Fredsøe, J. 2012 A wave generation toolbox for the opensource CFD library: OpenFoam. Intl J. Numer. Meth. Fluids 70 (9), 1073–1088.CrossRefGoogle Scholar
Jensen, B. L., Sumer, B. M. & Fredsøe, J. 1989 Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 206, 265–297.CrossRefGoogle Scholar
Jose, J., Choi, S. J., Erik, K., Giljarhus, T. & Gudmestad, O. T. 2017 A comparison of numerical simulations of breaking wave forces on a monopile structure using finite difference and finite volume models. Ocean Engng 137, 78–88.CrossRefGoogle Scholar
von Kármán, T.1931 Mechanical similitude and turbulence. NACA Tech. Rep. 611.Google Scholar
Kristiansen, T. & Faltinsen, O. M. 2017 Higher harmonic wave loads on a vertical cylinder in finite water depth. J. Fluid Mech. 833, 773–805.CrossRefGoogle Scholar
Menter, F., Kuntz, M. & Langtry, R. 2003 Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transfer 4, 625–632.Google Scholar
Paulsen, B. T.2013 Efficient computations of wave loads on off shore structures. PhD thesis.Google Scholar
Paulsen, B. T., Bredmose, H. & Bingham, H. B. 2014a An efficient domain decomposition strategy for wave loads on surface piercing circular cylinders. Coast. Engng 86, 57–76.CrossRefGoogle Scholar
Paulsen, B. T., Bredmose, H., Bingham, H. B. & Jacobsen, N. G. 2014b Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 755, 1–34.CrossRefGoogle Scholar
Rainey, R. C. T. 2007 Weak or strong nonlinearity: the vital issue. J. Engng Maths 58 (1–4), 229–249.CrossRefGoogle Scholar
Riise, B. H., Grue, J., Jensen, A. & Johannessen, T. B. 2018 A note on the secondary load cycle for a monopile in irregular deep water waves. J. Fluid Mech. 849, R1.CrossRefGoogle Scholar
Rosetti, G. F., Vaz, G. & Fujarra, A. L. C. 2012 URANS calculations for smooth circular cylinder flow in a wide range of Reynolds numbers: solution verification and validation. J. Fluids Engng 134 (12), 121103.CrossRefGoogle Scholar
Stringer, R. M., Zang, J. & Hillis, A. J. 2014 Unsteady RANS computations of flow around a circular cylinder for a wide range of Reynolds numbers. Ocean Engng 87, 1–9.CrossRefGoogle Scholar
Sumer, B. M. & Fredsøe, J. 2006 Hydrodynamics Around Cylindrical Structures. World Scientific.CrossRefGoogle Scholar
Tromans, P. S., Anatruk, A. R. & Hagemeijer, P. 1991 A new model for the kinematics of large ocean waves application as a design wave. In Proceedings of the First International Offshore and Polar Engineering Conference, vol. 8, pp. 64–71.Google Scholar
Weller, H. G., Tabor, G., Jasak, H. & Fureby, C. 1998 A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12 (6), 620–631.CrossRefGoogle Scholar
Yang, Y. & Rockwell, D. 2002 Wave interaction with a vertical cylinder: spanwise flow patterns and loading. J. Fluid Mech. 460, 93–129.CrossRefGoogle Scholar
Ye, H. & Wan, D. 2017 Benchmark computations for flows around a stationary cylinder with high Reynolds numbers by RANS-overset grid approach. Appl. Ocean Res. 65, 315–326.CrossRefGoogle Scholar