Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T01:42:21.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective transition of steady flow over a square leading-edge plate

Published online by Cambridge University Press:  30 March 2012

Mark C. Thompson
Mark C. Thompson*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC 3800, Australia
*
†Email address for correspondence: mark.thompson@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Previous experimental studies have shown that the steady recirculation bubble that forms as the flow separates at the leading-edge corner of a long plate, becomes unsteady at relatively low Reynolds numbers of only a few hundreds. The reattaching shear layer irregularly releases two-dimensional vortices, which quickly undergo three-dimensional transition. Similar to the flow over a backward-facing step, this flow is globally stable at such Reynolds numbers, with transition to a steady three-dimensional flow as the first global instability to occur as the Reynolds number is increased to 393. Hence, it appears that the observed flow behaviour is governed by transient growth of optimal two-dimensional transiently growing perturbations (constructed from damped global modes) rather than a single three-dimensional unstable global mode. This paper quantifies the details of the transient growth of two- and three-dimensional optimal perturbations, and compares the predictions to other related cases examined recently. The optimal perturbation modes are shown to be highly concentrated in amplitude in the vicinity of the leading-edge corners and evolve to take the local shape of a Kelvin–Helmholtz shear-layer instability further downstream. However, the dominant mode reaches a maximum amplitude downstream of the position of the reattachment point of the shear layer. The maximum energy growth increases at 2.5 decades for each increment in Reynolds number of 100. Maximum energy growth of the optimal perturbation mode at a Reynolds number of 350 is greater than 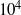, which is typically an upper limit of the Reynolds number range over which it is possible to observe steady flow experimentally. While transient growth analysis concentrates on the evolution of wavepackets rather than continuous forcing, this appears consistent with longitudinal turbulence levels of up to 1 % for some water tunnels, and the fact that the optimal mode is highly concentrated close to the leading-edge corner so that an instantaneous projection of a perturbation field from a noisy inflow onto the optimal mode can be significant. Indeed, direct simulations with inflow noise reveal that a root-mean-square noise level of just 0.1 % is sufficient to trigger some unsteadiness at 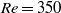, while a 0.5 % level results in sustained shedding. Three-dimensional optimal perturbation mode analysis was also performed showing that at 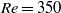, the optimal mode has a spanwise wavelength of 11.7 plate thicknesses and is amplified 20 % more than the two-dimensional optimal disturbance. The evolved three-dimensional mode shows strong streamwise vortical structures aligned at a shallow angle to the plate top surface.

JFM classification

Instability: Absolute/convective instability Instability: Nonlinear instability Wakes/Jets: Separated flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 698 , 10 May 2012 , pp. 335 - 357
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alam, M. & Sandham, N. D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 403, 223–250.CrossRefGoogle Scholar
2. Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for time steppers. Intl J. Numer. Meth. Fluids 57, 1435–1458.CrossRefGoogle Scholar
3. Barkley, D., Gomes, M. G. M. & Henderson, R. D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.CrossRefGoogle Scholar
4. Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
5. Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008a Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.CrossRefGoogle Scholar
6. Blackburn, H. M., Sherwin, S. J. & Barkley, D. 2008b Convective instability and transient growth in steady and pulsatile stenotic flow. J. Fluid Mech. 607, 267–277.CrossRefGoogle Scholar
7. Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4, 637–650.CrossRefGoogle Scholar
8. Cherubini, S., Robinet, J.-Ch. & Palma, P. De 2010 The effects of non-normality and nonlinearity of the Navier–Stokes operator on the dynamics of a large laminar separation bubble. Phys. Fluids 22, 014102.CrossRefGoogle Scholar
9. Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: nonnormality and nonlinearity. Ann. Rev. Fluid Mech. 37, 357.CrossRefGoogle Scholar
10. Chorin, A. J. 1968 Numerical solution of the Navier-Stokes equations. Maths Comput. 22, 745–762.CrossRefGoogle Scholar
11. Dušek, J., Frauníe, P. & Le Gal, P. 1994 Local analysis of the onset of instability in shear flows. Phys. Fluids 6 (1), 172–186.CrossRefGoogle Scholar
12. Ehrenstein, U. & Gallaire, F. 2008 Two-dimensional global low-frequency oscillations of a separating boundary layer flow. J. Fluid Mech. 614, 315–327.CrossRefGoogle Scholar
13. Gallaire, F., Marquillie, M. & Ehrenstein, U. 2006 Three-dimensional transverse instabilities in detached boundary layers. J. Fluid Mech. 571, 221–233.CrossRefGoogle Scholar
14. Gaster, M. 1966 The structure and behaviour of laminar separation bubbles. Tech. Rep. AGARD Publication CP-4 on Flow Separation: Part II.Google Scholar
15. Griffith, M. D., Leweke, T., Thompson, M. C. & Hourigan, K. 2008 Steady inlet flow in stenotic geometries: convective and absolute instabilities. J. Fluid Mech. 616, 111–133.CrossRefGoogle Scholar
16. Griffith, M. D., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 Convective instability in steady stenotic flow: optimal transient growth and experimental observation. J. Fluid Mech. 655, 504–514.CrossRefGoogle Scholar
17. Hourigan, K., Thompson, M. C. & Tan, B. T. 2001 Self-sustained oscillations in flows around long blunt plates. J. Fluids Struct. 15, 387–398.CrossRefGoogle Scholar
18. Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2008 Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J. Fluid Mech. 602, 175–207.CrossRefGoogle Scholar
19. Kaiktsis, L., Karniadakis, G. E. & Orszag, S. A. 1991 Onset of three-dimensionality, equilibria, and early transition in flow over a backward-facing step. J. Fluid Mech. 231, 501–528.CrossRefGoogle Scholar
20. Kaiktsis, L., Karniadakis, G. E. & Orszag, S. A 1996 Unsteadiness and convective instabilities in two-dimensional flow over a backward-facing step. J. Fluid Mech. 321, 157–187.CrossRefGoogle Scholar
21. Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods of the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.CrossRefGoogle Scholar
22. Lane, J. C. & Loehrke, R. I. 1980 Leading-edge separation from a blunt plate at low Reynolds number. ASME J. Fluids Engng 102 (11), 494–496.CrossRefGoogle Scholar
23. Lang, M., Rist, U. & Wagner, S. 2004 Investigations on controlled transition development in a laminar separation bubble by means of LDA and PIV. Exp. Fluids 36, 43–52.Google Scholar
24. Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.CrossRefGoogle Scholar
25. Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf-bifurcation in spherical Couette flow. Phys. Fluids 7 (1), 80–91.CrossRefGoogle Scholar
26. Marquet, O., Lombardi, M., Chomaz, J.-M., Sipp, D. & Jacquin, L. 2009 Direct and adjoint global modes of a recirculation bubble: lift-up and convective non-normalities. J. Fluid Mech. 622, 1–21.CrossRefGoogle Scholar
27. Marquet, O., Sipp, D., Chomaz, J.-M. & Jacquin, L. 2008 Amplifier and resonator dynamics of a low-Reynolds-number recirculation bubble in a global framework. J. Fluid Mech. 605, 429.CrossRefGoogle Scholar
28. Marxen, O. & Rist, U. 2010 Mean flow deformation in a laminar separation bubble: separation and stability characteristics. J. Fluid Mech. 660, 37–54.CrossRefGoogle Scholar
29. Mills, R., Sheridan, J. & Hourigan, K. 2003 Particle image velocimetry and visualization of natural and forced flow around rectangular cylinders. J. Fluid Mech. 478, 299–323.CrossRefGoogle Scholar
30. Nakamura, Y., Ohya, Y. & Tsurata, H. 1991 Experiments on vortex shedding from flat plates with square leading and trailing edges. J. Fluid Mech. 222, 437–447.CrossRefGoogle Scholar
31. Ohya, Y., Nakamura, Y., Ozone, S., Tsuruta, H. & Nakayama, R. 1992 A numerical study of vortex shedding from flat plates. J. Fluid Mech. 236, 445–460.CrossRefGoogle Scholar
32. Ota, T., Asano, Y. & Okawa, K. 1981 Reattachment length and transition of the separated flow over blunt flat plates. Bull. JSME 24 (192), 941–947.CrossRefGoogle Scholar
33. Ozono, S., Ohya, Y., Nakamura, Y. & Nakayama, R. 1992 Stepwise increase in the strouhal number for flows around flat plates. Intl J. Numer. Meth. Fluids 15, 1025–1036.CrossRefGoogle Scholar
34. Pauley, L. L., Moin, P. & Reynolds, W. C. 1990 The structure of two-dimensional separation. J. Fluid Mech. 220, 397–411.CrossRefGoogle Scholar
35. Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209.CrossRefGoogle Scholar
36. Ryan, K., Thompson, M. C. & Hourigan, K. 2005 Three-dimensional transition in the wake of elongated bluff bodies. J. Fluid Mech. 538, 1–29.CrossRefGoogle Scholar
37. Sasaki, K. & Kiya, M. 1991 Three-dimensional vortex structure in a leading-edge separation bubble at moderate Reynolds numbers. J. Fluids Engng 113, 405–410.CrossRefGoogle Scholar
38. Schmid, P. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129.CrossRefGoogle Scholar
39. Schmid, P. J. & Henningson, D. S. 2002 On the stability of a falling liquid curtain. J. Fluid Mech. 463, 163.CrossRefGoogle Scholar
40. Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003 From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J. Fluid Mech. 492, 147–180.CrossRefGoogle Scholar
41. Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004 From spheres to circular cylinders: non-axisymmetric transition in the flow past rings. J. Fluid Mech. 506, 45–78.CrossRefGoogle Scholar
42. Tan, B. T., Thompson, M. C. & Hourigan, K. 1998 Simulated flow around long rectangular plates under cross flow perturbations. Intl J. Fluid Dyn. 2 (1).Google Scholar
43. Tan, B. T., Thompson, M. C. & Hourigan, K. 2004 Flow past rectangular cylinders: receptivity to transverse forcing. J. Fluid Mech. 515, 33–62.CrossRefGoogle Scholar
44. Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006 Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30, 190–196.CrossRefGoogle Scholar
45. Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.CrossRefGoogle Scholar
46. Thompson, M. C., Leweke, T. & Provansal, M. 2001a Kinematics and dynamics of sphere wake transition. J. Fluids Struct. 15, 575–585.CrossRefGoogle Scholar
47. Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001b The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
48. Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.CrossRefGoogle ScholarPubMed