Fish escaping from predators exhibit amazing acceleration. The hydrodynamic mechanisms employed to power this acceleration are highlighted in the paper by Gazzola, van Rees & Koumoutsakos (J. Fluid Mech., this issue, vol. 698, 2012, pp. 5–17), showing that the fish bends its entire body and caudal fin, in order to entrap and then accelerate as large a mass of water as possible. It is also shown that hydrodynamic optimization drives the fast-start kinematics.

We investigate the C-start escape response of larval fish by combining flow simulations using remeshed vortex methods with an evolutionary optimization. We test the hypothesis of the optimality of C-start of larval fish by simulations of larval-shaped, two- and three-dimensional self-propelled swimmers. We optimize for the distance travelled by the swimmer during its initial bout, bounding the shape deformation based on the larval mid-line curvature values observed experimentally. The best motions identified within these bounds are in good agreement with in vivo experiments and show that C-starts do indeed maximize escape distances. Furthermore we found that motions with curvatures beyond the ones experimentally observed for larval fish may result in even larger escape distances. We analyse the flow field and find that the effectiveness of the C-start escape relies on the ability of pronounced C-bent body configurations to trap and accelerate large volumes of fluid, which in turn correlates with large accelerations of the swimmer.

We investigate homogeneous incompressible turbulence subjected to a range of degrees of stratification. Our basic method is pseudospectral direct numerical simulations at a resolution of . Such resolution is sufficient to reveal inertial power-law ranges for suitably comprised horizontal and vertical spectra, which are designated as the wave and vortex mode (the Craya–Herring representation). We study mainly turbulence that is produced from randomly large-scale forcing via an Ornstein–Uhlenbeck process applied isotropically to the horizontal velocity field. In general, both the wave and vortex spectra are consistent with a Kolmogorov-like range at sufficiently large . At large scales, and for sufficiently strong stratification, the wave spectrum is a steeper , while that for the vortex component is consistent with . Here is the horizontally gathered wavenumber. In contrast to the horizontal wavenumber spectra, the vertical wavenumber spectra show very different features. For those spectra, a clear dependence for small scales is observed while the large scales show rather flat spectra. By modelling the horizontal layering of vorticity, we attempt to explain the flat spectra. These spectra are linked to two-point structure functions of the velocity correlations in the horizontal and vertical directions. We can observe the power-law transition also in certain of the two-point structure functions.

We derive the closed system of averaged magnetohydrodynamic (MHD) equations for general oscillating flows. The used small parameter of our asymptotic theory is the dimensionless inverse frequency, and the leading term for a velocity field is chosen to be purely oscillating. The employed mathematical approach combines the two-timing method and the notion of a distinguished limit. The properties of commutators are used to simplify calculations. The derived averaged equations are similar to the original MHD equations, but surprisingly (instead of the commonly expected Reynolds stresses) a drift velocity plays a part of an additional advection velocity. In the special case of a vanishing magnetic field , the averaged equations produce the Craik–Leibovich equations for Langmuir circulations (which can be called ‘vortex dynamo’). We suggest that, since the mathematical structure of the full averaged equations for is similar to those for , these full equations could lead to a possible mechanism of MHD dynamo, such as the generation of the magnetic field of the Earth.

We examine the stability of two-dimensional marine ice sheets in steady state. The dynamics of marine ice sheets is described by a viscous thin-film model with two Stefan-type boundary conditions at the moving boundary or ‘grounding line’ that marks the transition from grounded to floating ice. One of these boundary conditions constrains ice thickness to be at a local critical value for flotation, which depends on depth to bedrock at the grounding line. The other condition sets ice flux as a function of ice thickness at the grounding line. Depending on the shape of the bedrock, multiple equilibria may be possible. Using a linear stability analysis, we confirm a long-standing heuristic argument that asserts that the stability of these equilibria is determined by a simple mass balance consideration. If an advance in the grounding line away from its steady-state position leads to a net mass gain, the steady state is unstable, and stable otherwise. This also confirms that grounding lines can only be stable in positions where bedrock slopes downwards sufficiently steeply.

The Lagally theorem describes the unsteady hydrodynamic force on a rigid body exhibiting arbitrary motion in an inviscid and incompressible fluid by the properties of the singularities employed to generate the flow and the body motion and to meet the boundary condition. So far, only sources and dipoles have been considered, and the present work extends the theorem to include free vortices in a two-dimensional flow. The present extension is validated by reproducing the system dynamics or the force evolution of three literature problems: (i) a free cylinder interacting with a free vortex; (ii) the moving Föppl problem; and (iii) a cylinder in constant normal approach to a fixed identical cylinder. This work further extends the bifurcation analysis on the moving Föppl problem by including the solid-to-liquid density ratio as a new parameter, in addition to the system total impulse and the vortex strength. We then apply the theorem to the problem where a moving Föppl system is made to approach a fixed or a free neutrally buoyant target cylinder of identical size from far away. The force developed on each cylinder is examined with respect to the vortex pair configuration and the target mobility. When approaching a fixed target, a greater force is developed if the vortex pair has stronger circulation and larger structure. The mobility of the target cylinder, however, can modify the hydrodynamic force by reducing its magnitude and reversing the force ordering with respect to the vortex pair configuration found for the case with fixed target. Possible mechanisms for such a change of force nature are given based on the currently derived equation of motion.

An experimental study of the pressure field generated by a subsonic, single stream, round jet is presented. The investigation is conducted in the near-field region at subsonic Mach numbers (up to 0.9) and Reynolds numbers . The main task of the present work is the analysis of the near-field acoustic pressure and the characterization of its spectral properties. To this aim, a novel post-processing technique based on the application of wavelet transforms is presented. The method accomplishes the separation of nearly Gaussian background fluctuations, interpreted as acoustic pressure, from intermittent pressure peaks induced by the hydrodynamic components. With respect to more standard approaches based on Fourier filtering, the new technique permits one to recover the whole frequency content of both the acoustic and the hydrodynamic contributions and to reconstruct them as independent signals in the time domain. The near-field acoustic pressure is characterized in terms of spectral content, sound pressure level and directivity. The effects of both the Mach number and the distance from the jet axis are analysed and the results are compared with published far-field observations and theoretical predictions. Simultaneous velocity/pressure measurements have been also performed using a hot-wire probe and a microphone pair in the near field. It is shown that the cross-correlation between the near-field acoustic pressure and the axial velocity is large (of the order of 0.2) in the potential core region whereas large velocity/hydrodynamic pressure correlations are located at the nozzle exit and downstream of the potential core.

We investigate the influence of a soluble surfactant on the steady-state motion of a finger of air through a compliant channel. This study provides a basic model from which to understand the fluid–structure interactions and physicochemical hydrodynamics of pulmonary airway reopening. Airway closure occurs in lung diseases such as respiratory distress syndrome and acute respiratory distress syndrome as a result of fluid accumulation and surfactant insufficiency. This results in ‘compliant collapse’ with the airway walls buckled and held in apposition by a liquid occlusion that blocks the passage of air. Airway reopening is essential to the recovery of adequate ventilation, but has been associated with ventilator-induced lung injury because of the exposure of airway epithelial cells to large interfacial flow-induced pressure gradients. Surfactant replacement is helpful in modulating this deleterious mechanical stimulus, but is limited in its effectiveness owing to slow surfactant adsorption. We investigate the effect of surfactant on micro-scale models of reopening by computationally modelling the steady two-dimensional motion of a semi-infinite bubble propagating through a liquid-filled compliant channel doped with soluble surfactant. Many dimensionless parameters affect reopening, but we primarily investigate how the reopening pressure depends upon the capillary number (the ratio of viscous to surface tension forces), the adsorption depth parameter (a bulk concentration parameter) and the bulk Péclet number (the ratio of bulk convection to diffusion). These studies demonstrate a dependence of on , and suggest that a critical bulk concentration must be exceeded to operate as a low-surface-tension system. Normal and tangential stress gradients remain largely unaffected by physicochemical interactions – for this reason, further biological studies are suggested that will clarify the role of wall flexibility and surfactant on the protection of the lung from atelectrauma.

We report experimental results on the dynamics of heavy particles of the size of the Kolmogorov scale in a fully developed turbulent flow. The mixed Eulerian structure function of two-particle velocity and acceleration difference vectors was observed to increase significantly with particle inertia for identical flow conditions. We show that this increase is related to a preferential alignment between these dynamical quantities. With increasing particle density the probability for those two vectors to be collinear was observed to grow. We show that these results are consistent with the preferential sampling of strain-dominated regions by inertial particles.

An experimental investigation to identify the source conditions that distinguish finite-volume negatively buoyant fluid projectile behaviour from fountain behaviour in quiescent environments of uniform density is described. Finite-volume releases are governed by their source Froude number and the aspect ratio of the release, where denotes the length of the column of fluid dispensed vertically from the nozzle of diameter . We establish the influence of on the peak rise heights of a release formed by dispensing saline solution into fresh water for and . Within these ranges, we determine the source conditions for which a flow may be regarded, in terms of the initial rise height attained, as either finite-volume or continuous flux. The critical aspect ratio , for a given , which when exceeded no longer influenced release behaviour, led to the determination of paired source conditions that give rise to solely Froude-number-dependent, i.e. fountain-like, behaviour. As such, we make the link between finite-volume releases and continuous fountains. The pairs led us directly to the classification of a space from which source conditions giving rise to either negatively buoyant projectiles or fountains may be readily identified. The variation of with corresponds closely to established fountain regimes of very weak, weak and forced fountains. Moreover, our results indicate that the formation or otherwise of a primary vortex, as fluid is ejected, has a profound influence on the length of the dispensed fluid column that is necessary to achieve rise heights equal to fountain rise heights.

In the present work, the features of liquid evaporation inside a low-porosity medium subjected to an impinging stream of hot gas is investigated analytically. The flow is analysed for a non-Darcy model, in which viscous and convective terms are considered in the Darcy pressure equation. A low-volatility liquid is considered, so that a low-vaporization regime is established. The rates of heat transfer between gas and solid and between liquid and solid are assumed to be high. Owing to differences between phase properties, in the system under study, different physical processes occur at different length scales. Using asymptotic expansions, expressions for the three phases that occur in this problem are obtained, in each of their length scales. The results predict that high injection temperatures are needed for phase change to occur, as a result of the low volatility of the liquid. Likewise, the enhancement of the vaporization rate due to heat conduction in the porous medium is quantified. The Hiemenz flow pressure term is modified to incorporate the effect of the porous medium, which is necessary for a solution to be found.

A study on the generation and development of high-amplitude steady streamwise streaks in a flat-plate boundary layer is presented. High-amplitude streamwise streaks are naturally present in many bypass transition scenarios, where they play a fundamental role in the breakdown to turbulence process. On the other hand, recent experiments and numerical simulations have shown that stable laminar streamwise streaks of alternating low and high speed are also capable of stabilizing the growth of Tollmien–Schlichting waves as well as localized disturbances and to delay transition. The larger the streak amplitude is, for a prescribed spanwise periodicity of the streaks, the stronger is the stabilizing mechanism. Previous experiments have shown that streaks of amplitudes up to 12 % of the free stream velocity can be generated by means of cylindrical roughness elements. Here we explore the possibility of generating streaks of much larger amplitude by using a row of miniature vortex generators (MVGs) similar to those used in the past to delay or even prevent boundary layer separation. In particular, we present a boundary layer experiment where streak amplitudes exceeding 30 % have been produced without having any secondary instability acting on them. Furthermore, the associated drag with the streaky base flow is quantified, and it is demonstrated that the streaks can be reinforced by placing a second array of MVGs downstream of the first one. In this way it is possible to make the control more persistent in the downstream direction. It must be pointed out that the use of MVGs opens also the possibility to set up a control method that acts twofold in the sense that both transition and separation are delayed or even prevented.

Fully developed incompressible turbulent pipe flow at Reynolds number (based on bulk velocity) and Kármán number is simulated in a periodic domain with a length of pipe radii . While single-point statistics match closely with experimental measurements, questions have been raised of whether streamwise energy spectra calculated from spatial data agree with the well-known bimodal spectrum shape in premultiplied spectra produced by experiments using Taylor’s hypothesis. The simulation supports the importance of large- and very large-scale motions (VLSMs, with streamwise wavelengths exceeding ). Wavenumber spectral analysis shows evidence of a weak peak or flat region associated with VLSMs, independent of Taylor’s hypothesis, and comparisons with experimental spectra are consistent with recent findings (del Álamo & Jiménez, J. Fluid Mech., vol. 640, 2009, pp. 5–26) that the long-wavelength streamwise velocity energy peak is overestimated when Taylor’s hypothesis is used. Yet, the spectrum behaviour retains otherwise similar properties to those documented based on experiment. The spectra also reveal the importance of motions of long streamwise length to the energy and Reynolds stress and support the general conclusions regarding these quantities formed using experimental measurements. Space–time correlations demonstrate that low-level correlations involving very large scales persist over in time and indicate that these motions convect at approximately the bulk velocity, including within the region approaching the wall. These very large streamwise motions are also observed to accelerate the flow near the wall based on force spectra, whereas smaller scales tend to decelerate the mean streamwise flow profile, in accordance with the behaviour observed in net force spectra of prior experiments. Net force spectra are resolved for the first time in the buffer layer and reveal an unexpectedly complex structure.

The isothermal Navier–Stokes equations are determined by the leading three velocity moments of the lattice Boltzmann method (LBM). Necessary conditions establishing the hydrodynamic consistency of these moments are provided by multiscale asymptotic techniques, such as the second-order Chapman–Enskog expansion. However, for simulating incompressible hydrodynamics the structure of the forcing term in the LBM is still a discordant issue as far as its correct velocity expansion order is concerned. This work uses the traditional second-order Chapman–Enskog expansion analysis to demonstrate that the truncation order of the forcing term may depend on the time regime in this case. This is due to the fact that LBM does not reproduce exactly the incompressibility condition. It rather approximates it through a weakly compressible or an artificial compressible system. The present study shows that for the artificial compressible setup, as the incompressibility flow condition is singularly perturbed by the time variable, such a connection will also affect the LBM forcing formulation. As a result, for time-independent incompressible flows the LBM forcing must be truncated to first order whereas for a time-dependent case it is convenient to include the second-order term. The theoretical findings are confirmed by numerical tests carried out in several distinct benchmark flows driven by space- and/or time-varying body forces and possessing known analytical solutions. These results are verified for the single relaxation time, the multiple relaxation time and the regularized collision models.

A new third-order solution for multi-directional irregular water waves in finite water depth is presented. The solution includes explicit expressions for the surface elevation, the amplitude dispersion and the vertical variation of the velocity potential. Expressions for the velocity potential at the free surface are also provided, and the formulation incorporates the effect of an ambient current with the option of specifying zero net volume flux. Harmonic resonance may occur at third order for certain combinations of frequencies and wavenumber vectors, and in this situation the perturbation theory breaks down due to singularities in the transfer functions. We analyse harmonic resonance for the case of a monochromatic short-crested wave interacting with a plane wave having a different frequency, and make long-term simulations with a high-order Boussinesq formulation in order to study the evolution of wave trains exposed to harmonic resonance.

Previous experimental studies have shown that the steady recirculation bubble that forms as the flow separates at the leading-edge corner of a long plate, becomes unsteady at relatively low Reynolds numbers of only a few hundreds. The reattaching shear layer irregularly releases two-dimensional vortices, which quickly undergo three-dimensional transition. Similar to the flow over a backward-facing step, this flow is globally stable at such Reynolds numbers, with transition to a steady three-dimensional flow as the first global instability to occur as the Reynolds number is increased to 393. Hence, it appears that the observed flow behaviour is governed by transient growth of optimal two-dimensional transiently growing perturbations (constructed from damped global modes) rather than a single three-dimensional unstable global mode. This paper quantifies the details of the transient growth of two- and three-dimensional optimal perturbations, and compares the predictions to other related cases examined recently. The optimal perturbation modes are shown to be highly concentrated in amplitude in the vicinity of the leading-edge corners and evolve to take the local shape of a Kelvin–Helmholtz shear-layer instability further downstream. However, the dominant mode reaches a maximum amplitude downstream of the position of the reattachment point of the shear layer. The maximum energy growth increases at 2.5 decades for each increment in Reynolds number of 100. Maximum energy growth of the optimal perturbation mode at a Reynolds number of 350 is greater than , which is typically an upper limit of the Reynolds number range over which it is possible to observe steady flow experimentally. While transient growth analysis concentrates on the evolution of wavepackets rather than continuous forcing, this appears consistent with longitudinal turbulence levels of up to 1 % for some water tunnels, and the fact that the optimal mode is highly concentrated close to the leading-edge corner so that an instantaneous projection of a perturbation field from a noisy inflow onto the optimal mode can be significant. Indeed, direct simulations with inflow noise reveal that a root-mean-square noise level of just 0.1 % is sufficient to trigger some unsteadiness at , while a 0.5 % level results in sustained shedding. Three-dimensional optimal perturbation mode analysis was also performed showing that at , the optimal mode has a spanwise wavelength of 11.7 plate thicknesses and is amplified 20 % more than the two-dimensional optimal disturbance. The evolved three-dimensional mode shows strong streamwise vortical structures aligned at a shallow angle to the plate top surface.

It has recently been suggested that the magneto-rotational instability (MRI) is a limiting case of the magneto-elliptic instability (MEI). This limit is obtained for horizontal modes in the presence of rotation and an external vertical magnetic field, when the aspect ratio of the elliptic streamlines tends to infinite. In this paper we unveil the link between these previously unconnected mechanisms, explaining both the MEI and the MRI as different manifestations of the same magneto-elliptic-rotational instability (MERI). The growth rates are found and the influence of the magnetic and rotational effects is explained, in particular the effect of the magnetic field on the range of negative Rossby numbers at which the horizontal instability is excited. Furthermore, we show how the horizontal rotational MEI in the rotating shear flow limit is linked to the MRI by the use of the local shearing box model, typically used in the study of accretion discs. In such a limit the growth rates of the two instability types coincide for any power-law-type background angular velocity radial profile with negative exponent corresponding to the value of the Rossby number of the rotating shear flow. The MRI requirement for instability is that the background angular velocity profile is a decreasing function of the distance from the centre of the disc, which corresponds to the horizontal rotational MEI requirement of negative Rossby numbers. Finally a physical interpretation of the horizontal instability, based on a balance between the strain, the Lorentz force and the Coriolis force, is given.

We derive a mathematical model of shear flows of shallow water down an inclined plane. The non-dissipative part of the model is obtained by averaging the incompressible Euler equations over the fluid depth. The averaged equations are simplified in the case of weakly sheared flows. They are reminiscent of the compressible non-isentropic Euler equations where the flow enstrophy plays the role of entropy. Two types of enstrophies are distinguished: a small-scale enstrophy generated near the wall, and a large-scale enstrophy corresponding to the flow in the roller region near the free surface. The dissipation is then added in accordance with basic physical principles. The model is hyperbolic, the corresponding ‘sound velocity’ depends on the flow enstrophies. Periodic stationary solutions to this model describing roll waves were obtained. The solutions are in good agreement with the experimental profiles of roll waves measured in Brock’s experiments. In particular, the height of the vertical front of the waves, the shock thickness and the wave amplitude are well captured by the model.

In microducts deviation from continuum flow behaviour of a gas increases with rarefaction. When using Navier–Stokes equations to calculate a flow under slightly and moderately rarefied conditions, slip boundary conditions are used which in turn refer to the tangential momentum accommodation coefficient (TMAC). Here we demonstrate that, in the so-called slip and transition regime, the flow in microducts can be reliably described by a consistently non-empirical model without considering the TMAC. We obtain this equation by superposition of convective transport and Fickian diffusion using two-dimensional solutions of Navier–Stokes equations and a description for the Knudsen diffusion coefficient as derived from kinetic theory respectively. For a wide variety of measurement series found in the literature the calculation predicts the data accurately. Surprisingly only size of the duct, temperature, gas properties and inlet and outlet pressure are necessary to calculate the resulting mass flow by means of a single algebraic equation. From this, and taking the discrepancies of the TMAC concerning surface roughness and nature of the gases into account, we could conclude that neither the diffusive proportions nor the total mass flow rates are influenced by surface topology and chemistry at Knudsen numbers below unity. Compared to the tube geometry, the model slightly underestimates the flow rate in rectangular channels when rarefaction increases. Likewise, the dimensionless mass flow rate and the diffusive proportion of the total flow are distinctly higher in a tube. Thus the cross-sectional geometry has a significant influence on the transport mechanisms under rarefied conditions.

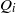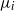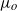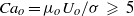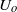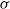We report experiments in which a flow rate of a fluid with a viscosity discharges into an immiscible liquid of viscosity that flows in parallel with the axis of the injector. When the outer capillary number verifies the condition , where and indicate, respectively, the outer velocity and the interfacial tension coefficient, and if the inner-to-outer velocity ratio is such that 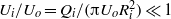, with 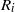the inner radius of the injector, a jet is formed with the same type of cone–jet geometry as predicted by the numerical results of Suryo & Basaran (Phys. Fluids, vol. 18, 2006, p. 082102). For extremely low values of the velocity ratio 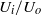, we find that the diameter of the jet emanating from the tip of the cone is so small that drops with sizes below 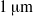can be formed. We also show that, through this simple method, concentrated emulsions composed of micrometre-sized drops with a narrow size distribution can be generated. Moreover, thanks to the information extracted from numerical simulations of boundary-integral type and using the slender-body approximation due to Taylor (Proceedings of the 11th International Congress of Applied Mechanics, Munich, 1964, pp. 790–796), we deduce a third-order, ordinary differential equation that predicts, for arbitrary values of the three dimensionless numbers that control this physical situation, namely, 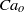, 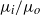and 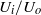, the shape of the jet and the sizes of the drops generated. Most interestingly, the influence of the geometry of the injector system on the jet shape and drop size enters explicitly into the third-order differential equation through two functions that can be easily calculated numerically. Therefore, our theory can be used as an efficient tool for the design of new emulsification devices.