Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T17:19:21.734Z Has data issue: false hasContentIssue false
  • English
  • Français

Global instability in the onset of transonic-wing buffet

Published online by Cambridge University Press:  24 October 2019

J. D. Crouch Open the ORCID record for J. D. Crouch [Opens in a new window] ,
A. Garbaruk  and
M. Strelets
J. D. Crouch*
Affiliation:
The Boeing Company, Seattle, WA 98124-2207, USA
A. Garbaruk
Affiliation:
Saint Petersburg State Polytechnic University, St. Petersburg, 195220, Russia
M. Strelets
Affiliation:
Saint Petersburg State Polytechnic University, St. Petersburg, 195220, Russia
*
†Email address for correspondence: jeffrey.d.crouch@boeing.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Global stability analysis is used to analyse the onset of transonic buffet on infinite swept and unswept wings. This high-Reynolds-number flow is governed by the unsteady Reynolds averaged Navier–Stokes equations. The analysis generalizes earlier studies focused on two-dimensional airfoils. For the unswept wing, results show spanwise-periodic stationary modes in addition to the earlier-observed oscillatory mode. The oscillatory mode is nominally two-dimensional with a spanwise wavelength greater than ten wing chords. The stationary modes of instability exist over two bands of spanwise wavelengths centred around an intermediate wavelength of one wing chord, and around a short wavelength of one tenth of a wing chord. The intermediate-wavelength modes have a flow structure characteristic of airfoil buffeting modes, concentrated at the shock and in the shear layer downstream of the shock. The short-wavelength modes are only concentrated in the shear layer downstream of the shock. These stationary modes can lead to spanwise-periodic flow structures for the unswept wing. For the swept wing, these stationary modes become unsteady travelling modes and contribute to the more complex buffeting-flow structures observed on swept wings as compared with unswept wings. The spanwise-wavelength bands of the travelling modes translate to different frequencies, resulting in a broad-banded unsteady response for the swept wing. For a 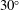$30^{\circ }$ swept wing, the frequencies associated with the intermediate-wavelength modes are approximately 10 times higher than the swept-wing generalization of the long-wavelength oscillatory mode, and approximately 6 times higher than the long-wavelength mode for the unswept wing. These instability characteristics are in good agreement with experimental observations.

JFM classification

Aerodynamics: High-speed flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 3 - 22
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartels, R. E. & Edwards, J. W.1997 Cryogenic tunnel pressure measurements on a supercritical airfoil for several shock buffet conditions. NASA Tech. Mem. 110272.Google Scholar
Benoit, B. & Legrain, I.1987 Buffeting prediction for transport aircraft applications based on unsteady pressure measurements. AIAA Paper 87-2356.10.2514/6.1987-2356Google Scholar
Crouch, J. D., Garbaruk, A. & Magidov, D. 2007 Predicting the onset of flow unsteadiness based on global instability. J. Comput. Phys. 224, 924–940.10.1016/j.jcp.2006.10.035Google Scholar
Crouch, J. D., Garbaruk, A., Magidov, D. & Travin, A. 2009a Origin of transonic buffet on aerofoils. J. Fluid Mech. 628, 357–369.10.1017/S0022112009006673Google Scholar
Crouch, J. D., Garbaruk, A., Magidov, D. & Jacquin, L. 2009b Global structure of buffeting flow on transonic airfoils. In IUTAM Symposium on Unsteady Separated Flows and Their Control, pp. 297–306. Springer.10.1007/978-1-4020-9898-7_25Google Scholar
Dandois, J. 2016 Experimental study of transonic buffet phenomenon on a 3D swept wing. Phys. Fluids 28, 1985–1994.Google Scholar
Deck, S. 2005 Numerical simulation of transonic buffet over a supercritical airfoil. AIAA J. 43, 1556–1566.10.2514/1.9885Google Scholar
Garbaruk, A. & Crouch, J. D. 2011 Quasi-three dimensional analysis of global instabilities: onset of vortex shedding behind a wavy cylinder. J. Fluid Mech. 677, 572–588.10.1017/jfm.2011.102Google Scholar
Giannelis, N. F., Vio, G. A. & Levinski, O. 2017 A review of recent developments in the understanding of transonic shock buffet. Prog. Aeronaut. Sci. 92, 39–84.10.1016/j.paerosci.2017.05.004Google Scholar
Gioria, R. S., He, W., Perez, J. M. & Theofilis, V.2016 Modal and non-modal global instability analysis of low-Re massively separated flow around a NACA 0015 airfoil. AIAA Paper 2016-3778.10.2514/6.2016-3778Google Scholar
Herbert, Th. 1983 On perturbation methods in nonlinear stability theory. J. Fluid Mech. 126, 167–186.10.1017/S0022112083000099Google Scholar
Hernandez, V., Roman, J. E., Tomas, A. & Vidal, V.2007 Krylov–Schur methods in slepc. SLEPc Tech. Rep., http://slepc.upv.es/documentation/reports/str7.pdf.Google Scholar
Iorio, M. C., Gonzalaz, L. M. & Ferrer, F. 2014 Direct and adjoint global stability analysis of turbulent transonic flows over a NACA0012 profile. Intl J. Numer. Meth. Fluids 76, 147–168.10.1002/fld.3929Google Scholar
Iovnovich, M. & Raveh, D. E. 2014 Numerical study of shock buffet on three-dimensional wings. AIAA J. 53, 449–463.10.2514/1.J053201Google Scholar
Jackson, C. P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.10.1017/S0022112087002234Google Scholar
Jacquin, L., Molton, P., Deck, S., Maury, B. & Soulevant, D. 2009 Experimental study of shock oscillation over a transonic supercritical profile. AIAA J. 47, 1985–1994.10.2514/1.30190Google Scholar
McDevitt, J. B. & Okuno, A. F.1985 Static and dynamic pressure measurements on a NACA0012 airfoil in the Ames high Reynolds number facility. NASA Tech. Paper 2485.Google Scholar
Molton, P., Dandois, J., Lepage, A., Brunet, V. & Bur, R. 2013 Control of buffet phenomenon on a transonic swept wing. AIAA J. 51, 761–772.Google Scholar
Ohmichi, Y., Ishida, T. & Hashimoto, A.2017 Numerical investigation of transonic buffet on a three-dimensional wing using incremental mode decomposition. AIAA Paper 2017-1436.10.2514/6.2017-1436Google Scholar
Plante, F., Laurendeau, E., Dandois, J. & Sartor, F.2017 Study of three-dimensional transonic buffet on swept wings. AIAA Paper 2017-3903.Google Scholar
Plante, F., Dandois, J. & Laurendeau, E.2019 Similitude between 3D cellular patterns in transonic buffet and subsonic stall. AIAA Paper 2019-0300.Google Scholar
Poplingher, L. & Raveh, D. E.2018 Modal analysis of transonic shock buffet on 2D airfoil. AIAA Paper 2018-2910.10.2514/6.2018-2910Google Scholar
Rodriguez, D. & Theofilis, V. 2011 On the birth of stall cells on airfoils. Theor. Comput. Fluid Dyn. 25, 105–117.10.1007/s00162-010-0193-7Google Scholar
Roe, P. L. 1981 Approximate Riemann solvers, parameters vectors and difference schemes. J. Comput. Phys. 43, 357–372.10.1016/0021-9991(81)90128-5Google Scholar
Sartor, F., Mettot, C. & Sipp, D. 2015 Stability, receptivity and sensitivity analysis of buffeting transonic flow over a profile. AIAA J. 53, 1980–1993.10.2514/1.J053588Google Scholar
Sartor, F. & Timme, S. 2017 Delayed detached-eddy simulation on shock buffet on half wing-body configuration. AIAA J. 55, 1230–1240.10.2514/1.J055186Google Scholar
Shur, M., Spalart, P. R., Squires, K. D., Strelets, M. & Travin, A. 2000 Three-dimensionality in Reynolds-averaged Navier–Stokes solutions around two-dimensional geometries. AIAA J. 43, 1230–1242.10.2514/1.9694Google Scholar
Shur, M., Strelets, M. & Travin, A. 2004 High-order implicit multi-block Navier–Stokes code: ten-years experience of application to RANS/DES/LES/DNS of turbulent flows. In 7th Symposium on Overset Composite Grids and Solution Technology.Google Scholar
Spalart, P. R.2000 Trends in turbulence treatments. AIAA Paper 2000-2306.10.2514/6.2000-2306Google Scholar
Spalart, P. R. & Allmaras, S. R. 1994 A one-equation turbulence model for aerodynamic flows. La Recherche Aérospatiale 1, 5–21; also AIAA Paper 92-0439.Google Scholar
Spalart, P. R., Belyaev, K., Garbaruk, A., Shur, M., Strelets, M. & Travin, A. 2017 Large-eddy and direct numerical simulations of the Bachalo–Johnson flow with shock-induced separation. Flow Turbul. Combust. 39, 865–885.10.1007/s10494-017-9832-zGoogle Scholar
Spalart, P. R., Strelets, M. & Travin, A. 2006 Direct numerical simulation of large-eddy-break-up devices in a boundary layer. Intl J. Heat Fluid Flow 27, 902–910.10.1016/j.ijheatfluidflow.2006.03.014Google Scholar
Sugioka, Y., Koike, S., Nakakita, K., Numata, D., Nonomura, T. & Asai, K. 2018 Experimental analysis of transonic buffet on a 3D swept wing using fast-response pressure-sensitive paint. Exp. Fluids 59, 108, 1–20.10.1007/s00348-018-2565-5Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.10.1146/annurev-fluid-122109-160705Google Scholar
Thiery, M. & Coustols, E. 2006 Numerical prediction of shock induced oscillations over a 2D airfoil: influence of turbulence modeling and test section walls. Intl J. Heat Fluid Flow 27, 661–670.10.1016/j.ijheatfluidflow.2006.02.013Google Scholar
Timme, S.2018 Global instability of wing shock buffet. Arxiv e-prints, arXiv:1806.07299 (physics.flu-dyn).Google Scholar
Timme, S.2019 Global shock buffet instability on NASA common research model. AIAA Paper 2019-0037.10.2514/6.2019-0037Google Scholar
Zebib, A. 1987 Stability of viscous flow past a circular cylinder. J. Engng Maths 21, 155–165.10.1007/BF00127673Google Scholar