Article contents
Linear and weakly nonlinear analyses of cylindrical Couette flow with axial and radial flows
Published online by Cambridge University Press: 06 July 2017
Abstract
Extending previous linear stability analyses of the instabilities developing in permeable Taylor–Couette–Poiseuille flows where axial and radial throughflows are superimposed on the usual Taylor–Couette flow, we further examine the linear behaviour and expand the analysis to consider the weakly nonlinear behaviour of convective-type instabilities by means of the derivation of the fifth-order amplitude equation together with direct numerical simulations. Special attention is paid to the influence of the radius ratio 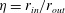 $\unicode[STIX]{x1D702}=r_{in}/r_{out}$ , and particularly to wide gaps (small
$\unicode[STIX]{x1D702}=r_{in}/r_{out}$ , and particularly to wide gaps (small 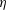 $\unicode[STIX]{x1D702}$ ) and how they magnify the effects of the radial flow. The instabilities take the form of pairs of counter-rotating toroidal vortices superseded by helical ones as the axial flow is increased. Increasing the radial inflow draws these vortices near the inner cylinder, where they shrink relative to the annular gap, when this gap is wide. Strong axial and radial flows in a narrow annular gap lead to a very large azimuthal wavenumber with steeply sloped helical vortices. Strong radial outflow in a wide annular gap results in very large helical vortices. The analytical and numerical saturated vortices match quite well. In addition, radial inflows or outflows can turn the usually supercritical bifurcation from laminar to vortical flow into a subcritical one. The radial flow above which this change occurs decreases as the radius ratio
$\unicode[STIX]{x1D702}$ ) and how they magnify the effects of the radial flow. The instabilities take the form of pairs of counter-rotating toroidal vortices superseded by helical ones as the axial flow is increased. Increasing the radial inflow draws these vortices near the inner cylinder, where they shrink relative to the annular gap, when this gap is wide. Strong axial and radial flows in a narrow annular gap lead to a very large azimuthal wavenumber with steeply sloped helical vortices. Strong radial outflow in a wide annular gap results in very large helical vortices. The analytical and numerical saturated vortices match quite well. In addition, radial inflows or outflows can turn the usually supercritical bifurcation from laminar to vortical flow into a subcritical one. The radial flow above which this change occurs decreases as the radius ratio 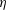 $\unicode[STIX]{x1D702}$ decreases. A practical motivation for this weakly nonlinear analysis is found in modelling dynamic filtration devices, which rely on vortical instabilities to reduce the processes of accumulation on their membranes.
$\unicode[STIX]{x1D702}$ decreases. A practical motivation for this weakly nonlinear analysis is found in modelling dynamic filtration devices, which rely on vortical instabilities to reduce the processes of accumulation on their membranes.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 16
- Cited by


