Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T07:14:55.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-local energy transfers in rotating turbulence at intermediate Rossby number

Published online by Cambridge University Press:  23 November 2011

L. Bourouiba ,
D. N. Straub  and
M. L. Waite
L. Bourouiba*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology Cambridge, MA 02139-4307, USA
D. N. Straub
Affiliation:
Department of Atmospheric and Oceanic Sciences, McGill University, Montréal, QC H3A 2K6, Canada
M. L. Waite
Affiliation:
Department of Applied Mathematics, University of Waterloo, 200 University Avenue West, Waterloo, Ontario N2L 3G1, Canada
*
†Email address for correspondence: lbouro@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent flows subject to solid-body rotation are known to generate steep energy spectra and two-dimensional columnar vortices. The localness of the dominant energy transfers responsible for the accumulation of the energy in the two-dimensional columnar vortices of large horizontal scale remains undetermined. Here, we investigate the scale-locality of the energy transfers directly contributing to the growth of the two-dimensional columnar structures observed in the intermediate Rossby number (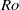) regime. Our approach is to investigate the dynamics of the waves and vortices separately: we ensure that the two-dimensional columnar structures are not directly forced so that the vortices can result only from association with wave to vortical energy transfers. Detailed energy transfers between waves and vortices are computed as a function of scale, allowing the direct tracking of the role and scales of the wave–vortex nonlinear interactions in the accumulation of energy in the large two-dimensional columnar structures. It is shown that the dominant energy transfers responsible for the generation of a steep two-dimensional spectrum involve direct non-local energy transfers from small-frequency small-horizontal-scale three-dimensional waves to large-horizontal-scale two-dimensional columnar vortices. Sensitivity of the results to changes in resolution and forcing scales is investigated and the non-locality of the dominant energy transfers leading to the emergence of the columnar vortices is shown to be robust. The interpretation of the scaling law observed in rotating flows in the intermediate- 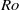regime is revisited in the light of this new finding of dominant non-locality.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Rotating turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 690 , 10 January 2012 , pp. 129 - 147
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Asselin, R. 1972 Frequency filter for time integrations. Mon. Weath. Rev. 100, 487–490.Google Scholar
2. Babin, A., Mahalov, A. & Nicolaenko, B. 1996 Global splitting, integrability and regularity of 3d euler and Navier–Stokes equations for uniformly rotating fluids. Eur. J. Mech. (B/Fluids) 15, 291–300.Google Scholar
3. Babin, A., Mahalov, A. & Nicolaenko, B. 2000 Global regularity of 3d rotating Navier–Stokes equations for resonant domains. Appl. Maths Lett. 13, 51–57.CrossRefGoogle Scholar
4. Bardina, J., Ferziger, J. H. & Rogallo, R. S. 1985 Effect of rotation on isotropic turbulence: computation and modelling. J. Fluid Mech. 154, 321–336.CrossRefGoogle Scholar
5. Bartello, P., Métais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1–29.CrossRefGoogle Scholar
6. Bellet, F., Godeferd, F., Scott, J. & Cambon, C. 2006 Wave-turbulence in rapidly rotating flows. J. Fluid Mech. 562, 83–121.Google Scholar
7. Bewley, G. P., Lathrop, D. P., Maas, L. R. M. & Screenivasan, K. R. 2007 Inertial waves in rotating grid turbulence. Phys. Fluids 19, 071701-1–071701-4.Google Scholar
8. Bourouiba, L. 2008a Discreteness and resolution effects in rapidly rotating turbulence. Phys. Rev. E 78, 056309-1–056309-12.Google Scholar
9. Bourouiba, L. 2008b Model of truncated fast rotating flow at infinite Reynolds number. Phys. Fluids 20, 075112-1–075112-14.Google Scholar
10. Bourouiba, L. & Bartello, P. 2007 The intermediate Rossby number range and 2d–3d transfers in rotating decaying homogeneous turbulence. J. Fluid Mech. 587, 139–161.Google Scholar
11. Boyd, J. P. 1989 Chebyshev & Fourier Spectral Methods. Springer.Google Scholar
12. Cambon, C. & Scott, J. F. 1999 Linear and nonlinear models of anisotropic turbulence. Annu. Rev. Fluid Mech. 31, 1–53.CrossRefGoogle Scholar
13. Canuto, V. M. & Dubovikov, M. S. 1997 Physical regimes and dimensional structure of rotating turbulence. Phys. Rev. Lett. 78, 666–669.Google Scholar
14. Chen, Q., Chen, S., Eyink, G. L. & Holm, D. D. 2005 Resonant interactions in rotating homogeneous three-dimensional turbulence. J. Fluid Mech. 542, 139–164.Google Scholar
15. Chertkov, M., Connaughton, C., Kolokolov, I. & Lebedev, V. 2007 Dynamics of energy condensation in two-dimensional turbulence. Phys. Rev. Lett. 99, 084501-1–084501-4.Google Scholar
16. Domaradski, J. A. 1988 Analysis of energy transfer in direct numerical simulations of isotropic turbulence. Phys. Fluids 31, 2747–2749.Google Scholar
17. Domaradzki, J. A. & Carati, D. 2007 An analysis of the energy transfer and the locality of nonlinear interactions in turbulence. Phys. Fluids 19 (8), 085112.CrossRefGoogle Scholar
18. Greenspan, H. P. 1968 The Theory of Rotating Fluid. Cambridge University Press.Google Scholar
19. Hide, R. & Ibbertson, A. 1966 An experimental study of Taylor columns. Icarus 5, 279–290.CrossRefGoogle Scholar
20. Hopfinger, E. J., Browand, K. F. & Gagne, Y. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.Google Scholar
21. Hossain, M. 1994 Reduction in the dimensionality of turbulence due to strong rotation. Phys. Fluids 6, 1077–1080.Google Scholar
22. Ibbetson, A. & Tritton, D. J. 1975 Experiments on turbulence in a rotating fluid. J. Fluid Mech. 68, 639–672.Google Scholar
23. Jacquin, L., Leuchter, O., Cambon, C. & Mathieu, J. 1990 Homogeneous turbulence in the presence of rotation. J. Fluid Mech. 220, 1–52.Google Scholar
24. Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
25. Lesieur, M. 1997 Turbulence in Fluids, 3rd edn. Kluwer.CrossRefGoogle Scholar
26. McEwan, A. D. 1976 Angular momentum diffusion and the initiation of cyclones. Nature 260, 126–128.Google Scholar
27. Mininni, P. D., Alexakis, A. & Pouquet, A. 2009 Scale interactions and scaling laws in rotating flows at moderate rossby numbers and large Reynolds numbers. Phys. Fluids 21 (1), 015108.Google Scholar
28. Morize, C. & Moisy, F. 2006 Energy decay of rotating turbulence with confinement effects. Phys. Fluids 18, 065107-1–065107-9.Google Scholar
29. Nazarenko, S. & Laval, J.-P. 2000 Non-local two-dimensional turbulence and batchelor’s regime for passive scalars. J. Fluid Mech. 403, 301–321.CrossRefGoogle Scholar
30. Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
31. Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.Google Scholar
32. Staplehurst, P. J., Davidson, P. A. & Dalziel, S. B. 2008 Structure formation in homogeneous freely decaying rotating turbulence. J. Fluid Mech. 598, 81–105.Google Scholar
33. Thiele, M. & Müller, W.-C. 2009 Structure and decay of rotating homogeneous turbulence. J. Fluid Mech. 637, 425–442.Google Scholar
34. Waleffe, F. 1993 Inertial transfers in the helical decomposition. Phys. Fluids 5, 677–685.CrossRefGoogle Scholar
35. Watanabe, T. I. T. & Shepherd, T. G. 2001 Infrared dynamics of decaying two-dimensional turbulence governed by the Charney–Hasegawa–Mima equation. J. Phys. Soc. Japan 70, 376–386.Google Scholar
36. Yeung, P. K. & Zhou, Y. 1998 Numerical study of rotating turbulence with external forcing. Phys. Fluids 10, 2895–2909.Google Scholar
37. Zhou, Y. 1993a Degrees of locality of energy transfer in the inertial range. Phys. Fluids A 5 (5), 1092–1094.Google Scholar
38. Zhou, Y. 1993b Interacting scales and energy transfer in isotropic turbulence. Phys. Fluids A 5, 2511–2524.Google Scholar
39. Zhou, Y. 1995 A phenomenological treatment of rotating turbulence. Phys. Fluids 7, 2092–2094.Google Scholar