The splash resulting from the impact of a drop onto a pool is a particularly beautiful manifestation of a canonical problem, where a mass of fluid breaks up into smaller pieces. Despite over a century of experimental study, the splashing mechanics have eluded full description, the details often being obscured by the very rapid motions and small length scales involved. Zhang et al. (J. Fluid Mech., vol. 690, 2012, pp. 5–15) introduce a powerful new tool to the experimental arsenal, when they apply X-ray imaging to study the fine ejecta sheets which emerge during the earliest contact of the drop. Their images reveal hidden details and complex underlying dynamics, which will directly affect the size and velocity of the splashing droplets.

We used optical and X-ray imaging to observe the formation of jets from the impact of a single drop with a deep layer of the same liquid. For high Reynolds number there are two distinct jets: the thin, fast and early-emerging ejecta; and the slow, thick and late-emerging lamella. For low Reynolds number the two jets merge into a single continuous jet, the structure of which is determined by the distinct contributions of the lamella and the ejecta. We measured the emergence time, position and speed of the ejecta sheet, and find that these scale as power laws with the impact speed and the viscosity. We identified the origin of secondary droplets with the breakup of the lamella and the ejecta jets, and show that the size of the droplets is not a good indicator of their origin.

We investigate the behaviour of linear plane waves in multilayer shallow water equations that include a complete treatment of the Coriolis force. These equations improve upon the conventional shallow water equations, based on the traditional approximation, that include only the part of the Coriolis force due to the locally vertical component of the rotation vector. Including the complete Coriolis force leads to dramatic changes in the structure of long linear plane waves. It allows subinertial waves to exist with frequencies below the inertial frequency, the minimum frequency for which waves exist under the traditional approximation. These subinertial waves are characterized by a distinguished limit in which the horizontal pressure gradient becomes comparable to the upwellings and downwellings driven by the non-traditional Coriolis term in the vertical momentum equation. The subinertial waves connect wave modes that remain separate in the conventional multilayer shallow water equations, such as the surface and internal waves in a two-layer system. Eastward-propagating surface waves in a two-layer system connect with westward-propagating internal waves, and vice versa, via the long subinertial waves. The long subinertial waves cannot be classified as either surface or internal waves, due to the phase difference between the disturbances to the interfaces in these waves.

The dynamics of the orientations of prolate ellipsoids in general linear shear flow is considered. The motivation behind this work is to gain a better understanding of the motion and the orientation probability distribution of ice particles in clouds in order to improve the modelling of their collision. The evolution of the orientations is governed by the Jeffery equation. It is shown that the possible attractors of this equation are fixed points, limit cycles and an infinite set of periodic solutions, named Jeffery orbits, in the case of simple shear. Linear stability analysis shows that the existence and the stability of the attractors are determined by the eigenvalues of the linear part of the equation. If the eigenvalues possess a non-vanishing real part, then there always exists either a stable fixed point or a stable limit cycle. Pure imaginary eigenvalues lead to Jeffery orbits. The convergence to a stable fixed point or to a stable limit cycle may either be monotonic or may be retarded due to the occurrence of non-normal growth. If non-normal growth occurs the convergence rate may be much slower compared with the characteristic time scale of the shear. Expressions for the characteristic time scale of convergence to the stable solutions are derived. In the case of non-normal growth, expressions are derived for the delay in the convergence. The orientation probability distribution function (p.d.f.) is computed via the solution of the Fokker–Planck equation. The p.d.f. is either periodic, in the case of simple shear (pure imaginary eigenvalues), or it converges to singular points or strips in the orientation space (fixed points and limit cycles) on which it grows to infinity. Time-independent p.d.f.s exist only for imaginary eigenvalues. Unlike the case where Brownian diffusion is present, the steady solutions are not unique and depend on the initial conditions.

The interaction between a turbulent flow and a granular bed via sediment transport produces various bedforms associated with distinct hydrodynamical regimes. In this paper, we compare ripples (downstream-propagating transverse bedforms), chevrons and bars (bedforms inclined with respect to the flow direction) and antidunes (upstream-propagating bedforms), focusing on the mechanisms involved in the early stages of their formation. Performing the linear stability analysis of a flat bed, we study the asymptotic behaviours of the dispersion relation with respect to the physical parameters of the problem. 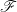In the subcritical regime (Froude number smaller than unity), we show that the same instability produces ripples or chevrons depending on the influence of the free surface. The transition from transverse to inclined bedforms is controlled by the ratio of the saturation length 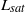, which encodes the stabilizing effect of sediment transport, to the flow depth 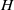, which determines the hydrodynamical regime. These results suggest that alternate bars form in rivers during flooding events, when suspended load dominates over bedload. In the supercritical regime 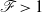, the transition from ripples to antidunes is also controlled by the ratio 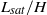. Antidunes appear around resonant conditions for free surface waves, a situation for which the sediment transport saturation becomes destabilizing. This resonance turns out to be fundamentally different from the inviscid prediction. Their wavelength selected by linear instability mostly scales on the flow depth 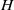, which is in agreement with existing experimental data. Our results also predict the emergence, at large Froude numbers, of ‘antichevrons’ or ‘antibars’, i.e. bedforms inclined with respect to the flow and propagating upstream.

Turbulent flows subject to solid-body rotation are known to generate steep energy spectra and two-dimensional columnar vortices. The localness of the dominant energy transfers responsible for the accumulation of the energy in the two-dimensional columnar vortices of large horizontal scale remains undetermined. 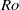Here, we investigate the scale-locality of the energy transfers directly contributing to the growth of the two-dimensional columnar structures observed in the intermediate Rossby number () regime. Our approach is to investigate the dynamics of the waves and vortices separately: we ensure that the two-dimensional columnar structures are not directly forced so that the vortices can result only from association with wave to vortical energy transfers. Detailed energy transfers between waves and vortices are computed as a function of scale, allowing the direct tracking of the role and scales of the wave–vortex nonlinear interactions in the accumulation of energy in the large two-dimensional columnar structures. It is shown that the dominant energy transfers responsible for the generation of a steep two-dimensional spectrum involve direct non-local energy transfers from small-frequency small-horizontal-scale three-dimensional waves to large-horizontal-scale two-dimensional columnar vortices. Sensitivity of the results to changes in resolution and forcing scales is investigated and the non-locality of the dominant energy transfers leading to the emergence of the columnar vortices is shown to be robust. The interpretation of the scaling law observed in rotating flows in the intermediate- 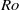regime is revisited in the light of this new finding of dominant non-locality.

From rain storms to ink jet printing, it is ubiquitous that a high-speed liquid droplet creates a splash when it impacts on a dry solid surface. Yet, the fluid mechanical mechanism causing this splash is unknown. About fifty years ago it was discovered that corona splashes are preceded by the ejection of a thin fluid sheet very near the vicinity of the contact point. Here we present a first-principles description of the mechanism for sheet formation, the initial stages of which occur before the droplet physically contacts the surface. We predict precisely when sheet formation occurs on a smooth surface as a function of experimental parameters, along with conditions on the roughness and other parameters for the validity of the predictions. The process of sheet formation provides a semi-quantitative framework for studying the subsequent events and the influence of liquid viscosity, gas pressure and surface roughness. The conclusions derived from this framework are in quantitative agreement with previous measurements of the splash threshold as a function of impact parameters (the size and velocity of the droplet) and in qualitative agreement with the dependence on physical properties (liquid viscosity, surface tension, ambient gas pressure, etc.) Our analysis predicts an as yet unobserved series of events within micrometres of the impact point and microseconds of the splash.

We consider the transition between the steady vertical path and the oscillatory path of two-dimensional bodies moving under the effect of buoyancy in a viscous fluid. Linearization of the Navier–Stokes equations governing the flow past the body and of Newton’s equations governing the body dynamics leads to an eigenvalue problem, which is solved numerically. Three different body geometries are then examined in detail, namely a quasi-infinitely thin plate, a plate of rectangular cross-section with an aspect ratio of 8, and a rod with a square cross-section. Two kinds of eigenmodes are observed in the limit of large body-to-fluid mass ratios, namely ‘fluid’ modes identical to those found in the wake of a fixed body, which are responsible for the onset of vortex shedding, and four additional ‘aerodynamic’ modes associated with much longer time scales, which are also predicted using a quasi-static model introduced in a companion paper. The stability thresholds are computed and the nature of the corresponding eigenmodes is investigated throughout the whole possible range of mass ratios. For thin bodies such as a flat plate, the Reynolds number characterizing the threshold of the first instability and the associated Strouhal number are observed to be comparable with those of the corresponding fixed body. Other modes are found to become unstable at larger Reynolds numbers, and complicated branch crossings leading to mode switching are observed. On the other hand, for bluff bodies such as a square rod, two unstable modes are detected in the range of Reynolds number corresponding to wake destabilization. For large enough mass ratios, the leading mode is similar to the vortex shedding mode past a fixed body, while for smaller mass ratios it is of a different nature, with a Strouhal number about half that of the vortex shedding mode and a stronger coupling with the body dynamics.

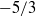Large-eddy simulations of single-shock-driven mixing suggest that, for sufficiently high incident Mach numbers, a two-gas mixing layer ultimately evolves to a late-time, fully developed turbulent flow, with Kolmogorov-like inertial subrange following a power law. After estimating the kinetic energy injected into the diffuse density layer during the initial shock–interface interaction, we propose a semi-empirical characterization of fully developed turbulence in such flows, based on scale separation, as a function of the initial parameter space, as 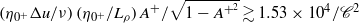, which corresponds to late-time Taylor-scale Reynolds numbers 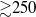. In this expression, 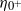represents the post-shock perturbation amplitude, 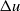the change in interface velocity induced by the shock refraction, the characteristic kinematic viscosity of the mixture, 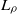the inner diffuse thickness of the initial density profile, 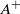the post-shock Atwood ratio, and 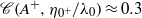for the gas combination and post-shock perturbation amplitude considered. The initially perturbed interface separating air and SF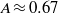6 (pre-shock Atwood ratio ) was impacted in a heavy–light configuration by a shock wave of Mach number 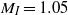, 1.25, 1.56, 3.0 or 5.0, for which is fixed at about 25 % of the dominant wavelength 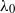of an initial, Gaussian perturbation spectrum. Only partial isotropization of the flow (in the sense of turbulent kinetic energy and dissipation) is observed during the late-time evolution of the mixing zone. For all Mach numbers considered, the late-time flow resembles homogeneous decaying turbulence of Batchelor type, with a turbulent kinetic energy decay exponent 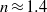and large-scale (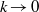) energy spectrum 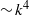, and a molecular mixing fraction parameter, 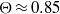. An appropriate time scale characterizing the Taylor-scale Reynolds number decay, as well as the evolution of mixing parameters such as 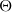and the effective Atwood ratio 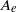, seem to indicate the existence of low- and high-Mach-number regimes.

Vesicles are drops of radius of a few tens of micrometres bounded by an impermeable lipid membrane of approximately 4 nm thickness in a viscous fluid. The salient characteristics of such a deformable object are a membrane rigidity governed by flexion due to curvature energy and a two-dimensional membrane fluidity characterized by a local membrane incompressibility. This provides unique properties with strong constraints on the internal volume and membrane area. Yet, when subjected to external stresses, vesicles exhibit a large deformability. The deformation of a settling vesicle in an infinite flow is studied theoretically, assuming a quasispherical shape and expanding all variables of the problem onto spherical harmonics. The contribution of thermal fluctuations is neglected in this analysis. A system of equations describing the temporal evolution of the shape is derived with this formalism. The final shape and the settling velocity are then determined and depend on two dimensionless parameters: the Bond number and the excess area. This simultaneous study leads to three stationary shapes, an egg-like shape already observed in an analogous experimental configuration in the limit of weak flow magnitude (Chatkaew, Georgelin, Jaeger & Leonetti, Phys. Rev. Lett, 2009, vol. 103(24), 248103), a parachute-like shape and a non-trivial non-axisymmetrical shape. The final shape depends on the initial conditions: prolate or oblate vesicle and orientation compared with gravity. The analytical solution in the small deformation regime is compared with numerical results obtained with a three-dimensional code. A very good agreement between numerical and theoretical results is found.

We study dynamo action in a convective layer of electrically conducting, compressible fluid, rotating about the vertical axis. At the upper and lower bounding surfaces, perfectly conducting boundary conditions are adopted for the magnetic field. Two different levels of thermal stratification are considered. If the magnetic diffusivity is sufficiently small, the convection acts as a small-scale dynamo. 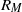Using a definition for the magnetic Reynolds number that is based upon the horizontal integral scale and the horizontally averaged velocity at the mid-layer of the domain, we find that rotation tends to reduce the critical value of 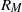above which dynamo action is observed. Increasing the level of thermal stratification within the layer does not significantly alter the critical value of 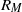in the rotating calculations, but it does lead to a reduction in this critical value in the non-rotating cases. At the highest computationally accessible values of the magnetic Reynolds number, the saturation levels of the dynamo are similar in all cases, with the mean magnetic energy density somewhere between 4 and 9 % of the mean kinetic energy density. To gain further insights into the differences between rotating and non-rotating convection, we quantify the stretching properties of each flow by measuring Lyapunov exponents. Away from the boundaries, the rate of stretching due to the flow is much less dependent upon depth in the rotating cases than it is in the corresponding non-rotating calculations. It is also shown that the effects of rotation significantly reduce the magnetic energy dissipation in the lower part of the layer. We also investigate certain aspects of the saturation mechanism of the dynamo.

We present high-resolution numerical simulations of the Euler and Navier–Stokes equations for a pair of colliding dipoles. We study the possible approach to a finite-time singularity for the Euler equations, and contrast it with the formation of developed turbulence for the Navier–Stokes equations. 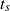We present numerical evidence that seems to suggest the existence of a blow-up of the inviscid velocity field at a finite time () with scaling 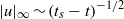, 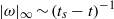. This blow-up is associated with the formation of a 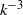spectral range, at least for the finite range of wavenumbers that are resolved by our computation. In the evolution toward 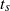, the total enstrophy is observed to increase at a slower rate, 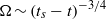, than would naively be expected given the behaviour of the maximum vorticity, 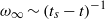. This indicates that the blow-up would be concentrated in narrow regions of the flow field. We show that these regions have sheet-like structure. Viscous simulations, performed at various 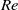, support the conclusion that any non-zero viscosity prevents blow-up in finite time and results in the formation of a dissipative exponential range in a time interval around the estimated inviscid 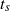. In this case the total enstrophy saturates, and the energy spectrum becomes less steep, approaching 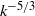. The simulations show that the peak value of the enstrophy scales as 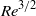, which is in accord with Kolmogorov phenomenology. During the short time interval leading to the formation of an inertial range, the total energy dissipation rate shows a clear tendency to become independent of 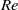, supporting the validity of Kolmogorov’s law of finite energy dissipation. At later times the kinetic energy shows a 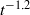decay for all 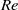, in agreement with experimental results for grid turbulence. Visualization of the vortical structures associated with the stages of vorticity amplification and saturation show that, prior to 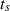, large-scale and the small-scale vortical structures are well separated. This suggests that, during this stage, the energy transfer mechanism is non-local both in wavenumber and in physical space. On the other hand, as the spectrum becomes shallower and a 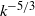range appears, the energy-containing eddies and the small-scale vortices tend to be concentrated in the same regions, and structures with a wide range of sizes are observed, suggesting that the formation of an inertial range is accompanied by transfer of energy that is local in both physical and spectral space.

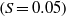We investigate global instability and vortex shedding in the separated laminar boundary layer beneath internal solitary waves (ISWs) of depression in a two-layer stratified fluid by performing high-resolution two-dimensional direct numerical simulations. The simulations were conducted with waves propagating over a flat bottom and shoaling over relatively mild and steep 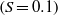slopes. Over a flat bottom, the potential for vortex shedding is shown to be directly dependent on wave amplitude, for a particular stratification, owing to increase of the adverse pressure gradient ( 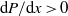for leftward propagating waves) beneath the trailing edge of larger amplitude waves. The generated eddies can ascend from the bottom boundary to as high as 33 % of the total depth in two-dimensional simulations. Over sloping boundaries, global instability occurs beneath all waves as they steepen. For the slopes considered, vortex shedding begins before wave breaking and the vortices, shed from the bottom boundary, can reach the pycnocline, modifying the wave breaking mechanism. Combining the results over flat and sloping boundaries, a unified criterion for vortex shedding in arbitrary two-layer continuous stratifications is proposed, which depends on the momentum-thickness Reynolds number and the non-dimensionalized ISW-induced pressure gradient at the point of separation. The criterion is generalized to a form that may be readily computed from field data and compared to published laboratory experiments and field observations. During vortex shedding events, the bed shear stress, vertical velocity and near-bed Reynolds stress were elevated, in agreement with laboratory observations during re-suspension events, indicating that boundary layer instability is an important mechanism leading to sediment re-suspension.

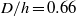A new type of flow-induced oscillation is reported for a tethered cylinder confined inside a Hele-Shaw cell (ratio of cylinder diameter to cell aperture, ) with its main axis perpendicular to the flow. This instability is studied numerically and experimentally as a function of the Reynolds number 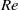and of the density 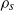of the cylinder. This confinement-induced vibration (CIV) occurs above a critical Reynolds number 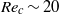much lower than for Bénard–Von Kármán vortex shedding behind a fixed cylinder in the same configuration (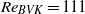). For low 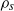values, CIV persists up to the highest 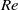value investigated (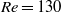). For denser cylinders, these oscillations end abruptly above a second value of 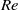larger than 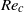and vortex-induced vibrations (VIV) of lower amplitude appear for 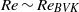. Close to the first threshold 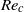, the oscillation amplitude variation as 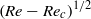and the lack of hysteresis demonstrate that the process is a supercritical Hopf bifurcation. Using forced oscillations, the transverse position of the cylinder is shown to satisfy a Van der Pol equation. The physical meaning of the stiffness, amplification and total mass coefficients of this equation are discussed from the variations of the pressure field.

It has previously been demonstrated that the drag experienced by a Poiseuille flow in a channel can be reduced by subjecting the flow to a dynamic regime of blowing and suction at the walls of the channel (also known as ‘transpiration’). Furthermore, it has been found to be possible to induce a ‘bulk flow’, or steady motion through the channel, via transpiration alone. In this work, we derive explicit asymptotic expressions for the induced bulk flow via a perturbation analysis. From this we gain insight into the physical mechanisms at work within the flow. The boundary conditions used are of travelling sine waves at either wall, which may differ in amplitude and phase. Here it is demonstrated that the induced bulk flow results from the effect of convection. We find that the most effective arrangement for inducing a bulk flow is that in which the boundary conditions at either wall are equal in magnitude and opposite in sign. We also show that, for the bulk flow induced to be non-negligible, the wavelength of the boundary condition should be comparable to, or greater than, the height of the channel. Moreover, we derive the optimal frequency of oscillation, for maximising the induced bulk flow, under such boundary conditions. The asymptotic behaviour of the bulk flow is detailed within the conclusion. It is found, under certain caveats, that if the amplitude of the boundary condition is too great, the bulk flow induced will become dependent only upon the speed at which the boundary condition travels along the walls of the channel. We propose the conjecture that for all similar flows, if the magnitude of the transpiration is sufficiently great, the bulk flow will depend only upon the speed of the boundary condition.

This paper presents an analytic expression for the acoustic eigenmodes of a cylindrical lined duct with rigid axially running splices in the presence of flow. The cylindrical duct is considered to be uniformly lined except for two symmetrically positioned axially running rigid liner splices. An exact analytic expression for the acoustic pressure eigenmodes is given in terms of an azimuthal Fourier sum, with the Fourier coefficients given by a recurrence relation. Since this expression is derived using a Green’s function method, the completeness of the expansion is guaranteed. A numerical procedure is described for solving this recurrence relation, which is found to converge exponentially with respect to number of Fourier terms used and is in practice quick to compute; this is then used to give several numerical examples for both uniform and sheared mean flow. An asymptotic expression is derived to directly calculate the pressure eigenmodes for thin splices. This asymptotic expression is shown to be quantitatively accurate for ducts with very thin splices of less than 1 % unlined area and qualitatively helpful for thicker splices of the order of 6 % unlined area. A thin splice is in some cases shown to increase the damping of certain acoustic modes. The influences of thin splices and thin boundary layers are compared and found to be of comparable magnitude for the parameters considered. Trapped modes at the splices are also identified and investigated.

We investigate the statistical properties of Rayleigh–Taylor turbulence in a three-dimensional convective cell of high aspect ratio, in which one transverse side is much smaller that the others. By means of high-resolution numerical simulation we study the development of the turbulent mixing layer and the scaling properties of the velocity and temperature fields. We show that the system undergoes a transition from a three- to two-dimensional turbulent regime when the width of the turbulent mixing layer becomes larger than the scale of confinement. In the late stage of the evolution the convective flow is characterized by the coexistence of Kolmogorov–Obukhov and Bolgiano–Obukhov scaling at small and large scales, respectively. These regimes are separated by the Bolgiano scale, which is determined by the scale of confinement of the flow. Our results show that the emergence of the Bolgiano–Obukhov scaling in Rayleigh–Taylor turbulence is connected to the onset of an upscale energy transfer induced by the geometrical constraint of the flow.

Although the acoustic analogy developed by Lighthill, Curle, and Ffowcs Williams and Hawkings for sound generation by unsteady flow past solid surfaces is formally exact, it has become accepted practice in aeroacoustics to use an approximate version in which viscous quadrupoles are neglected. Here we show that, when sound is radiated by non-rigid surfaces, and the smallest dimension is comparable to or less than the viscous penetration depth, neglect of the viscous-quadrupole term can cause large errors in the sound field. In addition, the interpretation of the viscous quadrupoles as contributing only to sound absorption is shown to be inaccurate. Comparisons are made with the scalar wave equation for linear waves in a viscous fluid, which is extended using generalized functions to describe the effects of solid surfaces. Results are also presented for two model problems, one in a half-space and one with simple cylindrical geometry, for which analytical solutions are available.

We examine the stability of the ‘coast’ motion of fish, that is to say, the motion of a neutrally buoyant fish at constant speed in a straight line. The forces and moments acting on the fish body are thus perfectly balanced. The fish motion is said to be unstable if a perturbation in the conditions surrounding the fish results in forces and moments that tend to increase the perturbation, and it is stable if these emerging forces tend to reduce the perturbation and return the fish to its original state. Stability may be achieved actively or passively. Active stabilization requires neurological control that activates musculo-skeletal components to compensate for the external perturbations acting against stability. Passive stabilization on the other hand requires no energy input by the fish and is dependent upon the fish morphology, i.e. geometry and elastic properties. In this paper, we use a deformable body consisting of an articulated body equipped with torsional springs at its hinge joints and submerged in an unbounded perfect fluid as a simple model to study passive stability as a function of the body geometry and spring stiffness. We show that for given body dimensions, the spring elasticity, when properly chosen, leads to passive stabilization of the (otherwise unstable) coast motion.

A theoretical study of the interaction term in the two-fluid model equations is presented. The relevant Navier–Stokes equation is volume-integrated in a control volume fixed in a field of dispersed two-phase flow; then it is time-integrated. An expression for the interaction term is obtained in the limit of infinitesimal control volume, which rigorously fits to the two-fluid model equation based on time averaging. The interaction term is then analysed for dispersed two-phase flow with homogeneous particle size. The mathematical expression of the resulting interaction term clearly shows its property, which has been overlooked for more than 40 years. It can be decomposed into the conventional interaction term and an additional ‘virtual force’ term. The virtual force term is evaluated approximately for two types of dispersed multiphase flow in order to demonstrate its effectiveness. The first is solid–liquid dispersed two-phase flow with spherical solid particles undergoing creeping flow, and the second is gas–liquid dispersed two-phase flow with large bubbles in a highly turbulent flow field. For solid spherical particles in a homogeneous creeping flow, the term vanishes, as was found numerically by Ten Cate and Sundaresan (Intl J. Multiphase Flow, vol. 32, 2006, pp. 106–131), although the term could be significant for a flow field with velocity gradient. For large bubbles in bubble columns in a recirculating turbulent flow regime, the term is significant. The two-fluid model equations are corrected by the introduction of these virtual force terms, which in some circumstances are important in simulating the macroscopic properties of dispersed two-phase flow with spatial variations.