Article contents
Stability of three-dimensional Gaussian vortices in an unbounded, rotating, vertically stratified, Boussinesq flow: linear analysis
Published online by Cambridge University Press: 05 July 2017
Abstract
The linear stability of three-dimensional vortices in rotating, stratified flows has been studied by analysing the non-hydrostatic inviscid Boussinesq equations. We have focused on a widely used model of geophysical and astrophysical vortices, which assumes an axisymmetric Gaussian structure for pressure anomalies in the horizontal and vertical directions. For a range of Rossby numbers ( 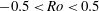 $-0.5<Ro<0.5$ ) and Burger numbers (
$-0.5<Ro<0.5$ ) and Burger numbers ( 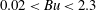 $0.02<Bu<2.3$ ) relevant to observed long-lived vortices, the growth rate and spatial structure of the most unstable eigenmodes have been numerically calculated and presented as a function of
$0.02<Bu<2.3$ ) relevant to observed long-lived vortices, the growth rate and spatial structure of the most unstable eigenmodes have been numerically calculated and presented as a function of 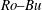 $Ro{-}Bu$ . We have found neutrally stable vortices only over a small region of the
$Ro{-}Bu$ . We have found neutrally stable vortices only over a small region of the 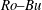 $Ro{-}Bu$ parameter space: cyclones with
$Ro{-}Bu$ parameter space: cyclones with 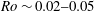 $Ro\sim 0.02{-}0.05$ and
$Ro\sim 0.02{-}0.05$ and 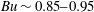 $Bu\sim 0.85{-}0.95$ . However, we have also found that anticyclones in general have slower growth rates compared to cyclones. In particular, the growth rate of the most unstable eigenmode for anticyclones in a large region of the parameter space (e.g.
$Bu\sim 0.85{-}0.95$ . However, we have also found that anticyclones in general have slower growth rates compared to cyclones. In particular, the growth rate of the most unstable eigenmode for anticyclones in a large region of the parameter space (e.g. 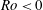 $Ro<0$ and
$Ro<0$ and 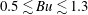 $0.5\lesssim Bu\lesssim 1.3$ ) is slower than 50 turnaround times of the vortex (which often corresponds to several years for ocean eddies). For cyclones, the region with such slow growth rates is confined to
$0.5\lesssim Bu\lesssim 1.3$ ) is slower than 50 turnaround times of the vortex (which often corresponds to several years for ocean eddies). For cyclones, the region with such slow growth rates is confined to 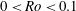 $0<Ro<0.1$ and
$0<Ro<0.1$ and 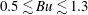 $0.5\lesssim Bu\lesssim 1.3$ . While most calculations have been done for
$0.5\lesssim Bu\lesssim 1.3$ . While most calculations have been done for 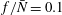 $f/\bar{N}=0.1$ (where
$f/\bar{N}=0.1$ (where 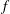 $f$ and
$f$ and 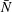 $\bar{N}$ are the Coriolis and background Brunt–Väisälä frequencies), we have numerically verified and explained analytically, using non-dimensionalized equations, the insensitivity of the results to reducing
$\bar{N}$ are the Coriolis and background Brunt–Väisälä frequencies), we have numerically verified and explained analytically, using non-dimensionalized equations, the insensitivity of the results to reducing 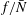 $f/\bar{N}$ to the more ocean-relevant value of 0.01. The results of our stability analysis of Gaussian vortices both support and contradict the findings of earlier studies with QG or multilayer models or with other families of vortices. The results of this paper provide a stepping stone to study the more complicated problems of the stability of geophysical (e.g. those in the atmospheres of giant planets) and astrophysical vortices (in accretion disks).
$f/\bar{N}$ to the more ocean-relevant value of 0.01. The results of our stability analysis of Gaussian vortices both support and contradict the findings of earlier studies with QG or multilayer models or with other families of vortices. The results of this paper provide a stepping stone to study the more complicated problems of the stability of geophysical (e.g. those in the atmospheres of giant planets) and astrophysical vortices (in accretion disks).
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 17
- Cited by


