Programming language semantics: It’s easy as 1,2,3

Abstract

Programming language semantics is an important topic in theoretical computer science, but one that beginners often find challenging. This article provides a tutorial introduction to the subject, in which the language of integers and addition is used as a minimal setting in which to present a range of semantic concepts in simple manner. In this setting, it is easy as 1,2,3.

1 Introduction

Semantics is the general term for the study of meaning. In computer science, the subject of programming language semantics seeks to give precise mathematical meaning to programs. When studying a new subject, it can be beneficial to begin with a simple example to understand the basic ideas. This article is about such an example that can be used to present a range of topics in programming language semantics: the language of simple arithmetic expressions built up from integers values using an addition operator.

This language has played a key role in my own work for many years. In the beginning, it was used to help explain semantic ideas, but over time it also became a mechanism to help discover new ideas and has featured in many of my publications. The purpose of this article is to consolidate this experience and show how the language of integers and addition can be used to present a range of semantic concepts in a simple manner.

Using a minimal language to explore semantic ideas is an example of Occam’s Razor (Duignan, 2018), a philosophical principle that favours the simplest explanation for a phenomenon. While the language of integers and addition does not provide features that are necessary for actual programming, it does provide just enough structure to explain many concepts from semantics. In particular, the integers provide a simple notion of ‘value’, and the addition operator provides a simple notion of ‘computation’. This language has been used by many authors in the past, such as McCarthy & Painter (1967), Wand (1982) and Wadler (1998), to name but a few. However, this article is the first to use the language as a general tool for exploring a range of different semantics topics.

Of course, one could consider a more sophisticated minimal language, such as a simple imperative language with mutable variables, or a simple functional language based on the lambda calculus. However, doing so then brings in other concepts such as stores, environments, substitutions and variable capture. Learning about these is important, but my experience time and time again is that there is much to be gained by first focusing on the simple language of integers and addition. Once the basic ideas are developed and understood in this setting, one can then extend the language with other features of interest, an approach that has proved useful in many aspects of the author’s own work.

The article written in a tutorial style does not assume prior knowledge of semantics and is aimed at the level of advanced undergraduates and beginning PhD students. Nonetheless, I hope that experienced readers will also find useful ideas for their own work. Beginners may wish to initially focus on sections 2–7, which introduce and compare a number of widely used approaches to semantics (denotational, small-step, contextual and big-step) and illustrate how inductive techniques can be used to reason about semantics. In turn, those with more experience may wish to proceed quickly through to section 8, which presents an extended example of how abstract machines can be systematically derived from semantics using the concepts of continuations and defunctionalisation.

Note that the article does not aim to provide a comprehensive account of semantics in either breadth or depth, but rather to summarise the basic ideas and benefits of the minimal approach, and provide pointers to further reading. Haskell is used throughout as a meta-language to implement semantic ideas, which helps to make the ideas more concrete and allows them to be executed. All the code is available online as Supplementary Material.

2 Arithmetic expressions

We begin by defining our language of interest, namely simple arithmetic expressions built up from the set $\mathbb{Z}$ of integer values using the addition operator $+$ . Formally, the language E of such expressions is defined by the following context-free grammar:

$$ E ~::=~ \mathbb{Z} \,\mid\, E + E $$

That is, an expression is either an integer value or the addition of two sub-expressions. We assume that parentheses can be freely used as required to disambiguate expressions written in normal textual form, such as $1+(2+3)$ . The grammar for expressions can also be translated directly into a Haskell datatype declaration, for which purpose we use the built-in type Integer of arbitrary precision integers:

For example, the expression $1+2$ is represented by the term ${\mathit{Add}\;(\mathit{Val}\;\mathrm{1})\;(\mathit{Val}\;\mathrm{2})}$ . From now on, we mainly consider expressions represented in Haskell.

3 Denotational semantics

In the first part of the article, we show how our simple expression language can be used to explain and compare a number of different approaches to specifying the semantics of languages. In this section, we consider the denotational approach to semantics (Scott & Strachey, 1971), in which the meaning of terms in a language is defined using a valuation function that maps terms into values in an appropriate semantic domain.

Formally, a denotational semantics for a language T of syntactic terms comprises two components: a set V of semantic values and a valuation function of type $T \rightarrow V$ that maps terms to their meaning as values. The valuation function is typically written by enclosing a term in semantic brackets, writing $[\![ t ]\!]$ for the result of applying the valuation function to the term t. The semantic brackets are also known as Oxford or Strachey brackets, after the pioneering work of Christopher Strachey on the denotational approach.

In addition to the above, the valuation function is required to be compositional, in the sense that the meaning of a compound term is defined purely in terms of the meaning of its subterms. Compositionality aids understanding by ensuring that the semantics is modular and supports the use of simple equational reasoning techniques for proving properties of the semantics. When the set of semantic values is clear, a denotational semantics is often identified with the underlying valuation function.

Arithmetic expressions of type Expr have a particularly simple denotational semantics, given by taking V as the Haskell type Integer of integers and defining a valuation function of type ${\mathit{Expr}}\rightarrow {\mathit{Integer}}$ by the following two equations:

The first equation states that the value of an integer is simply the integer itself, while the second states that the value of an addition is given by adding together the values of its two sub-expressions. This definition manifestly satisfies the compositionality requirement, because the meaning of a compound expression Add x y is defined purely by applying the ${\mathbin{+}}$ operator to the meanings of the two sub-expressions x and y.

Compositionality simplifies reasoning because it allows us to replace ‘equals by equals’. For example, our expression semantics satisfies the following property:

That is, we can freely replace the two argument expressions of an addition by other expressions with the same meanings, without changing the meaning of the addition as a whole. This property can be proved by simple equational reasoning using the definition of the valuation function and the assumptions about the argument expressions:

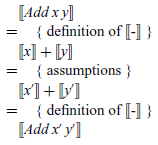
In practice, given that terms and their semantics are built up inductively, proofs about denotational semantics typically proceed using structural induction (Burstall, 1969). By way of example, let us show that our expression semantics is total, in the sense that for every expression e there is an integer n such that $[\![ e ]\!] = n$ .

The proof of totality proceeds by induction on the structure of the expression e. For the base case, ${\mathit{e}\mathrel{=}\mathit{Val}\;\mathit{n}}$ , the equation ${[\![\!\;\mathit{Val}\;\mathit{n}\;\!]\!]\mathrel{=}\mathit{n}}$ is trivially true by the definition of the valuation function. For the inductive case, ${\mathit{e}\mathrel{=}\mathit{Add}\;\mathit{x}\;\mathit{y}}$ , we can assume by induction that ${[\![ x ]\!]\mathrel{=}\mathit{n}}$ and ${[\![ y ]\!]\mathrel{=}\mathit{m}} for some integers {\mathit{n}}$ and ${\mathit{m}}$ , and it then follows using the valuation function that ${[\![\!\;\mathit{Add}\;\mathit{x}\;\mathit{y}\;\!]\!]\mathrel{=}[\![ x ]\!]\mathbin{+}[\![ y ]\!]\mathrel{=}\mathit{n}\mathbin{+}\mathit{m}}$ , which establishes this case is also true.

The valuation function can also be translated directly into a Haskell function definition, by simply rewriting the mathematical definition in Haskell notation:

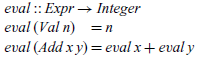
More generally, a denotational semantics can be viewed as an evaluator (or interpreter) that is written in a functional language. For example, using the above definition we have ${\mathit{eval}\;(\mathit{Add}\;(\mathit{Val}\;\mathrm{1})\;(\mathit{Add}\;(\mathit{Val}\;\mathrm{2})\;(\mathit{Val}\;\mathrm{3})))\mathrel{=}\mathrm{1}\mathbin{+}(\mathrm{2}\mathbin{+}\mathrm{3})\mathrel{=}\mathrm{6}}$ , or pictorially:

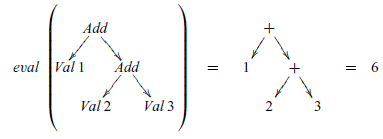
From this example, we see that an expression is evaluated by replacing each Add constructor by the addition function + on integers, and by removing each Val constructor, or equivalently, by replacing each Val by the identity function id on integers. That is, even though eval is defined recursively, because the semantics is compositional its behaviour can be understood as simply replacing the constructors for expressions by other functions. In this manner, a denotational semantics can also be viewed as an evaluation function that is defined by ‘folding’ over the syntax of the source language:

The fold operator (Meijer et al., 1991) captures the idea of replacing the constructors of the language by other functions, here replacing Val and Add by functions f and g:

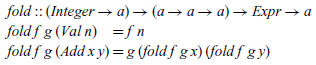
Note that a semantics defined using fold is compositional by definition, because the result of folding over an expression Add x y is defined purely by applying the given function g to the result of folding over the two argument expressions x and y.

We conclude this section with two further remarks. First of all, if we had chosen the grammar $E ::= \mathbb{Z} \mid E+E$ as our source language, rather than the type Expr, then the denotational semantics would have the following form:

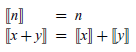
However, in this version the same symbol $+$ is now used for two different purposes: on the left side, it is a syntactic constructor for building terms, while, on the right side, it is a semantic operator for adding integers. We avoid such issues and keep a clear distinction between syntax and semantics by using the type Expr as our source language, which provides special-purpose constructors Val and Add for building expressions.

And secondly, note that the above semantics for expressions does not specify the order of evaluation, that is, the order in which the two arguments of addition should be evaluated. In this case, the order has no effect on the final value, but if we did wish to make evaluation order explicit this requires the introduction of additional structure into the semantics, which we will discuss when we consider abstract machines in Section 8.

Further reading. The standard reference on denotational semantics is Schmidt (1986), while Winskel’s (1993) textbook on formal semantics provides a concise introduction to the approach. The problem of giving a denotational semantics for the lambda calculus, in particular the technical issues that arise with recursively defined functions and types, led to the development of domain theory (Abramsky & Jung, 1994).

The idea of defining denotational semantics using fold operators is explored further in Hutton (1998). The simple integers and addition language has also been used as a basis for studying a range of other language features, including exceptions (Hutton & Wright, 2004), interrupts (Hutton & Wright, 2007), transactions (Hu & Hutton, 2009), nondeterminism (Hu & Hutton, 2010) and state (Bahr & Hutton, 2015).

4 Small-step semantics

Another popular approach to semantics is the operational approach (Plotkin, 1981), in which the meaning of terms is defined using an execution relation that specifies how terms can be executed in an appropriate machine model. There are two basic forms of operational semantics: small-step, which describes the individual steps of execution, and big-step, which describes the overall results of execution. In this section, we consider the small-step approach, which is also known as ‘structural operational semantics’, and will return to the big-step approach later on in Section 7.

Formally, a small-step operational semantics for a language T of syntactic terms comprises two components: a set S of execution states and a transition relation on S that relates each state to all states that can be reached by performing a single execution step. If two states s and s’ are related, we say that there is a transition from s to s’ and write this as $s \mathrel{{\longrightarrow}} s'$ . More general notions of transition relation are sometimes used, but this simple notion suffices for our purposes here. When the set of states is clear, an operational semantics is often identified with the underlying transition relation.

For example, arithmetic expressions have a simple small-step operational semantics, given by taking S as the Haskell type Expr of expressions and defining the transition relation on Expr by the following three inference rules:

The first rule states that two values can be added to give a single value and is called a reduction (or contraction) rule as it specifies how a basic operation is performed. An expression that matches such a rule is termed a reducible expression or ‘redex’. In turn, the last two rules permit transitions to be made on either side of an addition and are known as structural (or congruence) rules, as they specify how larger terms can be reduced.

Note that the semantics is non-deterministic, because an expression may have more than one possible transition. For example, the expression $(1+2) + (3+4)$ , written here in normal syntax for brevity, has two possible transitions, because the reduction rule can be applied on either side of the top-level addition using the two structural rules:

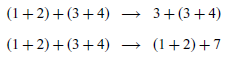
Such transitions change the syntactic form of an expression, but the underlying value of the expression remains the same, in this case 10. More formally, we can now capture a simple relationship between our denotational and small-step semantics for expressions, namely that making a transition does not change the denotation of an expression:

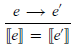
This property can be proved by induction on the structure of the expression e. For the base case, ${\mathit{e}\mathrel{=}\mathit{Val}\;\mathit{n}}$ , the result is trivially true because there is no transition rule for values in our small-step semantics, and hence the precondition $e \mathrel{{\longrightarrow}} e'$ cannot be satisfied. For the inductive case, ${\mathit{e}\mathrel{=}\mathit{Add}\;\mathit{x}\;\mathit{y}}$ , we proceed by performing a further case analysis, depending on which of the three inference rules for addition is applicable:

• • If the first inference rule is applicable, i.e. the precondition $e \mathrel{{\longrightarrow}} e'$ has the form ${\mathit{Add}\;(\mathit{Val}\;\mathit{n})\;(\mathit{Val}\;\mathit{m})}$ $\mathrel{{\longrightarrow}}$ ${\mathit{Val}\;(\mathit{n}\mathbin{+}\mathit{m})}$ , then the conclusion ${[\![\!\;\mathit{Add}\;(\mathit{Val}\;\mathit{n})\;(\mathit{Val}\;\mathit{m})\;\!]\!]\mathrel{=}[\![\!\;\mathit{Val}\;(\mathit{n}\mathbin{+}\mathit{m})\;\!]\!]}$ is true because both sides evaluate to ${\mathit{n}\mathbin{+}\mathit{m}}$ .

• • If the second rule is applicable, i.e. the precondition $e \mathrel{{\longrightarrow}} e'$ has the form ${\mathit{Add}\;\mathit{x}\;\mathit{y}}$ $\mathrel{{\longrightarrow}}$ Add x’ y for some transition $x \mathrel{{\longrightarrow}} x'$ , then we must show ${[\![\!\;\mathit{Add}\;\mathit{x}\;\mathit{y}\;\!]\!]\mathrel{=}[\![\!\;\mathit{Add}\;\mathit{x'}\;\mathit{y}\;\!]\!]}$ . Using the ‘equals by equals’ property of addition from the previous section, this equation holds if ${[\![ x ]\!]\mathrel{=}[\![ x' ]\!]} and {[\![ y ]\!]\mathrel{=}[\![ y ]\!]}$ , the first of which is true by induction based on the assumption $x \mathrel{{\longrightarrow}} x'$ , and the second of which is true by reflexivity.

• • If the third rule is applicable, the same form of reasoning as the second case can be used, except that the expression y makes a transition rather than x.

While the above proof is correct, it is rather cumbersome, as it involves quite a bit of case analysis. In the next section, we will see how to prove the relationship between the semantics in a simpler and more direct manner, using the principle of rule induction.

Evaluation of an expression using the small-step semantics proceeds by a series of zero or more transition steps. Formally, this is usually captured by taking the reflexive/transitive closure of the transition relation, written as ${\mathrel{{\stackrel{*}{\longrightarrow}}}}$ . For example, the fact that the expression above evaluates to 10 can be written using this notion as follows:

By repeated application of the transition relation, we can also generate a transition tree that captures all possible execution paths for an expression. For example, the expression above gives rise to the following tree, which captures the two possible execution paths:

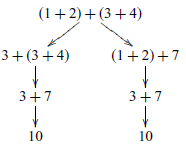
The transition relation can also be translated into a Haskell function definition, by exploiting the fact that a relation can be represented as a non-deterministic function that returns all possible values related to a given value. Using the list comprehension notation, it is straightforward to define a function that returns the list of all expressions that can be reached from a given expression by performing a single transition:

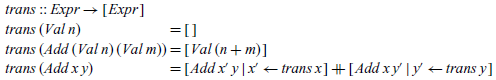
In turn, we can define a Haskell datatype for transition trees and an execution function that converts expressions into trees by repeated application of the transition function:

From this definition, we see that an expression is executed by taking the expression itself as the root of the tree and generating a list of residual expressions to be processed to give the subtrees by applying the trans function. That is, even though exec is defined recursively, its behaviour can be understood as simply applying the identity function to give the root of the tree and the transition function to generate a list of residual expressions to be processed to give the subtrees. In this manner, a small-step operational semantics can be viewed as giving rise to an execution function that is defined by ‘unfolding’ to transition trees:

The unfold operator (Gibbons & Jones, 1998) captures the idea of generating a tree from a seed value x by applying a function f to give the root and a function g to give a list of residual values that are then processed in the same way to produce the subtrees:

In summary, whereas denotational semantics corresponds to ‘folding over syntax trees’, operational semantics corresponds to ‘unfolding to transition trees’. Thinking about semantics in terms of recursion operators reveals a duality that might otherwise have been missed and still is not as widely known as it should be.

We conclude with three further remarks. First of all, note that if the original grammar for expressions was used as our source language rather than the type Expr, then the first inference rule for the semantics would have the following form:

However, this rule would be rather confusing unless we introduced some additional notation to distinguish the syntactic + on the left side from the semantic + on the right side, which is precisely what is achieved by the use of the Expr type.

Secondly, the above semantics for expressions does not specify the order of evaluation, or more precisely, it captures all possible evaluation orders. However, if we do wish to specify a particular evaluation order, it is straightforward to modify the inference rules to achieve this. For example, replacing the second Add rule by the following would ensure the first argument to addition is always evaluated before the second:

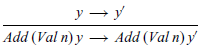
In contrast, as noted in the previous section, making evaluation order explicit in a denotational semantics requires additional structure. Being able to specify evaluation order in a straightforward manner is an important benefit of the small-step approach.

And finally, using Haskell as our meta-language the transition relation was implemented in an indirect manner as a non-deterministic function, in which the ordering of the equations is important because the patterns that are used are not disjoint. In contrast, if we used a meta-language with dependent types, such as Agda (Norell, 2007), the transition relation could be implemented directly as an inductive family (Dybjer, 1994), with no concerns about ordering in the definition. However, we chose to use Haskell rather than a more sophisticated language in order to make the ideas more accessible. Nonetheless, it is important to acknowledge the limitations of this choice.

Further reading. The origins of the operational approach to semantics are surveyed in Plotkin (2004). The small-step approach can be useful when the fine structure of execution is important, such as when considering concurrent languages (Milner, 1999), abstract machines (Hutton & Wright, 2006) or efficiency (Hope & Hutton, 2006). The idea of defining operational semantics using unfold operators, and the duality with denotational semantics defined using fold operators, is explored in Hutton (1998).

5 Rule induction

For denotational semantics, the basic proof technique is the familiar idea of structural induction, which allows us to perform proofs by considering the syntactic structure of terms. For operational semantics, the basic technique is the perhaps less familiar but just as useful concept of rule induction (Winskel, 1993), which allows us to perform proofs by considering the structure of the rules that are used to define the semantics.

We introduce the idea of rule induction using a simple numeric example and then show how it can be used to simplify the semantic proof from the previous section. We begin by inductively defining a set E of even natural numbers by the following two rules:

That first rule, the base case, states that the number 0 is the set E. The second rule, the inductive case, states that for any number n in E, the number $n+2$ is also in E. Moreover, the inductive nature of the definition means there is nothing in the set E beyond the numbers that can be obtained by applying these two rules a finite number of times, which is sometimes called the ‘extremal clause’ of the definition.

For the inductively defined set E, the principle of rule induction states that in order to prove that some property P holds for all elements of E, it suffices to show that P holds for 0, the base case, and that if P holds for any element $n \in E$ then it also holds for $n+2$ , the inductive case. That is, we have the following proof rule:

By way of example, we can use rule induction to verify a simple closure property of even numbers, namely that the addition of two even numbers is also even:

In order to prove this result, we first define the underlying property P, then apply rule induction, and finally expand out the definition of P to leave two conditions:

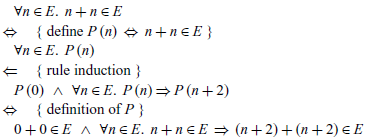
The first resulting condition simplifies to $0 \in E$ , which is trivially true by the first rule that defines the set E. In turn, for the second condition the concluding term can be rearranged to $((n+n)+2)+2 \in E$ , which by applying the second rule for E twice follows from $n+n \in E$ , which is true by assumption. Note that this closure property cannot be proved using normal mathematical induction on the natural numbers, because the property is only true for even numbers rather than for arbitrary naturals.

The concept of rule induction can easily be generalised to multiple base and inductive cases, to rules with multiple preconditions and so on. For example, for our small-step semantics of expressions, we have one base case and two inductive cases:

Hence, if we want to show that some property P (e,e’) on pairs of expressions holds for all transitions , we can use rule induction, which in this case has the form:

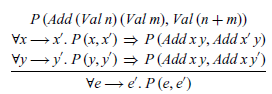
That is, we must show that P holds for the transition defined by the base rule of the semantics, that if P holds for the precondition transition for the first inductive rule then it also holds for the resulting transition, and similarly for the second inductive rule. Note that the three premises are presented vertically in the above rule for reasons of space, and we write $\forall x \mathrel{{\longrightarrow}} y.~ {\mathit{P}\;(\mathit{x},\mathit{y})}$ as shorthand for $\forall x,y.~\, x \mathrel{{\longrightarrow}} y \;\Rightarrow\; {\mathit{P}\;(\mathit{x},\mathit{y})}$ .

We can use the above rule induction principle to verify the relationship between the denotational and small-step semantics for expressions from the previous section, which can be expressed using our shorthand notation as follows:

To prove this result, we first define the underlying property P, then apply rule induction, and finally expand out the definition of P to leave three conditions:

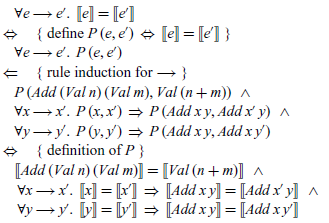
The three final conditions can then be verified by simple calculations over the denotational semantics for expressions, which we include below for completeness:

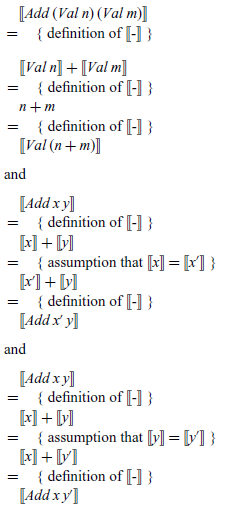
We conclude with two further remarks. First of all, when compared to the original proof by structural induction in Section 3, the above proof by rule induction is simpler and more direct. In particular, using structural induction, in the base case for Val n we needed to argue that the result is trivially true because there is no transition rule for values, while in the inductive case for Add x y we needed to perform a further case analysis depending on which of the three inference rules for addition is applicable. In contrast, using rule induction the proof proceeds directly on the structure of the transition rules, which is the key structure here and gives a proof with three cases, rather than the syntactic structure of expressions, which is secondary and results in a proof with two extra cases.

Secondly, just as proofs using structural induction do not normally proceed in full detail by explicitly defining a property and stating the induction principle being used, so the same is true with rule induction. For example, the above proof would often be abbreviated by simply stating that it proceeds by rule induction on the transition $e \mathrel{{\longrightarrow}} e'$ and then immediately stating and verifying the three conditions as above.

Further reading. Wright (2005) demonstrates how the principle of rule induction can be used to verify the equivalence of small- and big-step operational semantics for our simple expression language. The same idea can also be applied to more general languages, such as versions of the lambda calculus that count evaluation steps (Hope, 2008) or support a form of non-deterministic choice (Moran, 1998).

6 Contextual semantics

The small-step semantics for expressions in Section 4 has one basic reduction rule for adding values and two structural rules that allow addition to be performed in larger expressions. Separating these two forms of rules gives rise to the notion of contextual semantics, also known as a ‘reduction semantics’ (Felleisen & Hieb, 1992).

Informally, a context in this setting is a term with a ‘hole’, usually written as , which can be ‘filled’ with another term later on. In a contextual semantics, the hole represents the location where a single basic step of execution may take place within a term. For example, consider the following transition in our small-step semantics:

In this case, an addition is performed on the left side of the term. This idea can be made precise by saying that we can perform the basic step $1+2 \mathrel{{\longrightarrow}} 3$ in the context , where the hole indicates where the addition takes place. For arithmetic expressions, the language C of contexts can formally be defined by the following grammar:

That is, a context is either a hole or a context on either side of the addition of an expression. As previously, however, to keep a clear distinction between syntax and semantics we translate the grammar into a Haskell datatype declaration:

This style of context is known as ‘outside-in’, as locating the hole involves navigating from the outside of the context inwards. For example, the concept of filling the hole in a context c with an expression e, which we write as c [ e], can be defined as follows:

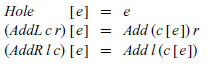
That is, if the context is a hole, we simply return the given expression; otherwise, we recurse on the left or right side of an addition as appropriate. Note that the above is a mathematical definition for hole filling, which uses Haskell syntax for contexts and expressions. As usual, we will see shortly how it can be implemented in Haskell itself.

Using the idea of hole filling, we can now redefine the small-step semantics for expressions in contextual style, by means of the following two inference rules:

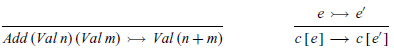
The first rule defines a reduction relation that captures the basic behaviour of addition, while the second defines a transition relation that allows the first rule to be applied in any context, that is, to either argument of an addition. In this manner, we have now refactored the small-step semantics into a single reduction rule and a single structural rule. Moreover, if we subsequently wished to extend the language with other features, this usually only requires adding new reduction rules and extending the notion of contexts but typically does not require adding new structural rules.

The contextual semantics can readily be translated into Haskell. Defining hole filling is just a matter of rewriting the mathematical definition in Haskell syntax:

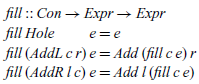
In turn, the dual operation, which splits an expression into all possible pairs of contexts and expressions, can be defined using the list comprehension notation:

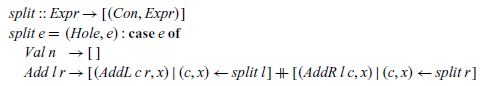
The behaviour of this function can be formally characterised as follows: a pair (c,x) comprising a context c and an expression x is an element of the list returned by split e precisely when fill c x=e. Using these two functions, the contextual semantics can then be translated into Haskell function definitions that return the lists of all expressions that can be reached by performing a single reduction step,

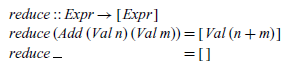
or a single transition step:

In particular, the function reduce implements the reduction rule for addition, while trans implements the contextual rule by first splitting the given expression into all possible context and expression pairs, then considering any reduction that can made by each component expression, and finally, filling the resulting expressions back into the context.

We conclude with two further remarks. First of all, although efficiency is not usually a primary concern when defining semantics, the small-step semantics for expressions in both original and contextual form perform rather poorly in terms of the amount of computation they require. In particular, evaluating an expression using these semantics involves a repeated process of finding the next point where a reduction step can be made, performing the reduction, and then filling the resulting expression back into the original term. This is clearly quite an inefficient way to perform evaluation.

And secondly, as with the original small-step semantics in the previous section, the contextual semantics does not specify an evaluation order for addition and is hence non-deterministic. However, if we do wish to specify a particular order, it is straightforward to modify the language of contexts to achieve this. For example, modifying the second case for addition as shown below (and adapting the notion of hole filling accordingly) would ensure the first argument to addition is evaluated before the second.

This version of the semantics also satisfies a unique decomposition property, namely that any expression e that is not a value can be uniquely decomposed into the form e=c [ x] for some context c and reducible expression x, which makes precise the sense in which there is at most one possible transition for any expression.

The unique decomposition property can be proved by induction on the expression e. For the base case, e=Val n, the property is trivially true as the expression is already a value. For the inductive case, e=Add l r, we construct a unique decomposition e=c [ x] by case analysis on the form of the two argument expressions l and r:

• • If l and r are both values, then and x=Add l r is the only possible decomposition of e=Add l r, as both subterms of e are values and hence not reducible.

• • If l is an addition, then by induction l can be uniquely decomposed into the form l=c’ [ x’] for some context c’ and reducible expression x’. Then c=c’+r and x=x’ is the only possible decomposition of e=Add l r, as the syntax for contexts specifies that we can only decompose r when l is a value, which it is not.

• • Finally, if l has the form Val n for some integer n, and r is an addition, then by induction r can be uniquely decomposed into the form r=c’ [ x’] for some context c’ and reducible expression x’. Then c=n+c’ and x=x’ is the only possible decomposition of e=Add l r, as l is already a value and hence cannot be decomposed.

We will see another approach to specifying evaluation order in Section 8 when we consider the idea of transforming semantics into abstract machines, which provide a small-step approach to evaluating expressions that is also more efficient.

Further reading. Contexts are related to a number of other important concepts in programming and semantics, including the use of continuations to make control flow explicit (Reynolds, 1972), navigating around data structures using zippers (Huet, 1997), deriving abstract machines from evaluators (Ager et al., 2003a ) and the idea of differentiating (Abbott et al., 2005) and dissecting (McBride, 2008) datatypes. We will return to some of these topics later on when we consider abstract machines.

7 Big-step semantics

Whereas small-step semantics focus on single execution steps, big-step semantics specify how terms can be fully executed in one large step. Formally, a big-step operational semantics, also known as a ‘natural semantics’ (Kahn, 1987), for a language T of syntactic terms comprises two components: a set V of values and an evaluation relation between T and V that relates each term to all values that can be reached by fully executing the term. If a term t and a value v are related, we say that t can evaluate to v and write this as $t \Downarrow v$ .

Arithmetic expressions of type Expr have a simple big-step operational semantics, given by taking V as the Haskell type Integer and defining the evaluation relation between Expr and Integer by the following two inference rules:

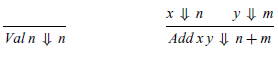
The first rule states that a value evaluates to the underlying integer, and the second that if two expressions x and y evaluate, respectively, to the integer values n and m, then the addition of these expressions evaluates to the integer n+m.

The evaluation relation can be translated into a Haskell function definition in a similar manner to the small-step semantics, by using the comprehension notation to return the list of all values that can be reached by executing a given expression to completion:

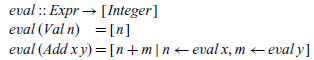
For our simple expression language, the big-step semantics is essentially the same as the denotational semantics from Section 3 but specified in a relational manner using inference rules rather than a functional manner using equations. However, there is no need for a big-step semantics to be compositional, whereas this is a key aspect of the denotational approach. This difference becomes evident when more sophisticated languages are considered. For example, the lambda calculus compiler in Bahr & Hutton (2015) is based on a non-compositional semantics specified in big-step form.

Formally, the fact that the denotational and big-step semantics for the expression language are equivalent can be captured by the following property:

That is, an expression denotes an integer value precisely when it evaluates to this value. To prove this result, we consider the two directions separately. In the left-to-right direction, the implication ${[\![ e ]\!]\mathrel{=}\mathit{n}\; \Rightarrow \;\mathit{e}\;\!\Downarrow\!\;\mathit{n}}$ can first be simplified by substituting the assumption ${\mathit{n}\mathrel{=}[\![ e ]\!]}$ into the conclusion ${\mathit{e}\;\!\Downarrow\!\;\mathit{n}} to give {\mathit{e}\;\!\Downarrow\!\;[\![ e ]\!]}$ , which property can then be verified by structural induction on the expression e. For the base case, ${\mathit{e}\mathrel{=}\mathit{Val}\;\mathit{n}}$ , we have

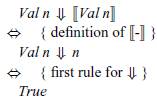
while for the inductive case, e=Add x y, we reason as follows:

Conversely, in the right-to-left direction, the implication ${\mathit{e}\;\!\Downarrow\!\;\mathit{n}\; \Rightarrow \;[\![ e ]\!]\mathrel{=}\mathit{n}}$ can first be rewritten in the form ${\forall\!\;\mathit{e}\;\!\Downarrow\!\;\mathit{n}\;\!.\,\;[\![ e ]\!]\mathrel{=}\mathit{n}}$ using the shorthand notation that was introduced in Section 5, which property can then be verified by rule induction on the big-step semantics for expressions. In particular, spelling the details out we have

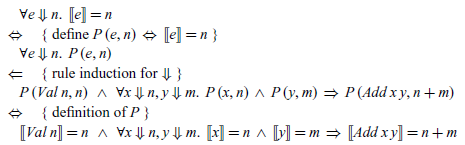
The two final conditions are then verified by simply applying the definition of [[ - ]].

Further reading. Big-step semantics can be useful in situations when we are only interested in the final result of execution rather than the detail of how this is performed. In this article, we primarily focus on denotational and operational approaches to semantics, but there are a variety of other approaches too, including axiomatic (Hoare, 1969), algebraic (Goguen & Malcolm, 1996), modular (Mosses, 2004), action (Mosses, 2005) and game (Abramsky & McCusker, 1999) semantics.

8 Abstract machines

All of the examples we have considered so far have been focused on explaining semantic ideas. In this section, we show how the language of integers and addition can also be used to help discover semantic ideas. In particular, we show how it can be used as the basis for discovering how to implement an abstract machine (Landin, 1964) for evaluating expressions in a manner that precisely defines the order of evaluation.

We begin by recalling the following simple evaluation function from Section 3:

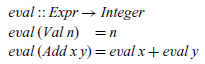
As noted previously, this definition does not specify the order in which the two arguments of addition are evaluated. Rather, this is determined by the implementation of the meta-language, in this case Haskell. If desired, the order of evaluation can be made explicit by constructing an abstract machine for evaluating expressions.

Formally, an abstract machine is usually defined by a set of syntactic rewrite rules that make explicit how each step of evaluation proceeds. In Haskell, this idea can be realised by mutually defining a set of first-order, tail recursive functions on suitable data structures. In this section, we show how an abstract machine for our simple expression language can be systematically derived from the evaluation function using a two-step process based on two important semantic concepts, continuations and defunctionalisation, using an approach that was pioneered by Danvy and his collaborators (Ager et al., 2003a ).

8.1 Step 1 – add continuations

The first step in producing an abstract machine for the expression language is to make the order of evaluation explicit in the semantics itself. A standard technique for achieving this aim is to rewrite the semantics in continuation-passing style (Reynolds, 1972).

In our setting, a continuation is a function that will be applied to the result of an evaluation. For example, in the equation eval (Add x y)=eval x+eval y from our semantics, when the first recursive call, eval x, is being evaluated, the remainder of the right-hand side of the equation, + eval y, can be viewed as a continuation for this evaluation, in the sense that it is the function that will be applied to the resulting value.

More formally, for our semantics eval::Expr → Integer, a continuation is a function of type Integer → Integer that will be applied to the resulting integer to give a new integer. This type can be generalised to Integer →a, but we do not need the extra generality here. We capture the notion of such a continuation using the following type declaration:

Our aim now is to define a new semantics, eval’, that takes an expression and returns an integer as previously but also takes a continuation as an additional argument, which is applied to the result of evaluating the expression. That is, we seek to define a function:

The desired behaviour of eval’ is captured by the following equation:

(1) \begin{eqnarray} {\mathit{eval'}\;\mathit{e}\;\mathit{c}} &=& {\mathit{c}\;(\mathit{eval}\;\mathit{e})} \end{eqnarray}

That is, applying eval’ to an expression and a continuation should give the same result as applying the continuation to the value of the expression.

At this point in most presentations, a recursive definition for eval’ would now be given, from which the above equation could then be proved. However, we can also view the equation as a specification for the function eval’, from which we then aim to discover or calculate a definition that satisfies the specification. Note that the above specification has many possible solutions, because the original semantics does not specify an evaluation order. We develop one possible solution below, but others are possible too.

To calculate the definition for eval’, we proceed from specification (1) by structural induction on the expression e. In each case, we start with the term eval’ e c and gradually transform it by equational reasoning, aiming to end up with a term t that does not refer to the original semantics eval, such that we can then take eval’ e c=t as a defining equation for eval’ in this case. For the base case, e=Val n, the calculation has just two steps:

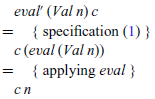
Hence, we have discovered the following definition for eval’ in the base case:

That is, if the expression is an integer value, we simply apply the continuation to this value. For the inductive case, e=Add x y, we begin in the same way as above:

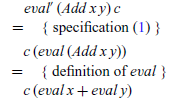
At this point, no further definitions can be applied. However, as we are performing an inductive calculation, we can use the induction hypotheses for the argument expressions x and y, namely that for all c’ and c”, we have eval’ x c’=c’ (eval x) and eval’ y c”=c” (eval y). In order to use these hypotheses, we must rewrite suitable parts of the term being manipulated into the form c’ (eval x) and c” (eval y) for some continuations c’ and c”. This can readily be achieved by abstracting over eval x and eval y using lambda expressions. Using these ideas, the rest of the calculation is then straightforward:

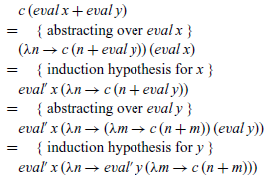
The final term now has the required form, i.e. does not refer to eval, and hence we have discovered the following definition for eval’ in the inductive case:

That is, if the expression is an addition, we evaluate the first argument x and call the result n, then evaluate the second argument y and call the result m, and finally apply the continuation c to the sum of n and m. In this manner, order of evaluation is now explicit in the semantics. In summary, we have calculated the following definition:

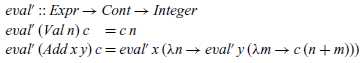
Finally, our original semantics can be recovered from our new semantics by substituting the identity continuation λn→n into specification (1) from which eval’ was constructed. That is, the original semantics eval can now be redefined as follows:

8.2 Step 2 – defunctionalise

We have now taken a step towards an abstract machine by making evaluation order explicit but in doing so have also taken a step away from such a machine by making the semantics into a higher-order function that takes a continuation as an additional argument. The second step is to regain the first-order nature of the original semantics by eliminating the use of continuations but retaining the explicit order of evaluation they introduced.

A standard technique for eliminating the use of functions as arguments is defunctionalisation (Reynolds, 1972). This technique is based upon the observation that we do not usually need the entire function-space of possible argument functions, because only a few forms of such functions are actually used in practice. Hence, we can represent the argument functions that we actually need using a datatype rather than using actual functions.

Within the definitions of the functions eval and eval’, there are only three forms of continuations that are used, namely one to end the evaluation process (λn→n), one to continue once the first argument of an addition has been evaluated (λn→eval’ y ) and one to add two integer results together (λm→c (n+m)). We begin by defining three combinators halt, next and add for constructing these forms of continuations:

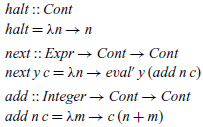
In each case, free variables in the continuation become parameters of the combinator. Using the above definitions, our continuation semantics can now be rewritten as:

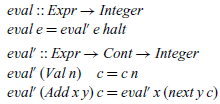
The next stage in the process is to declare a first-order datatype whose constructors represent the three combinators, which can easily be achieved as follows:

Note that the constructors for CONT have the same names and types as the combinators for Cont, except that all the items are now capitalised. The fact that values of type CONT represent continuations of type Cont is formalised by the following translation function, which forms a denotational semantics for the new datatype:

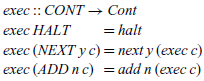
In the literature, this function is usually called apply (Reynolds, 1972), reflecting the fact that when its type is expanded to CONT → Integer → Integer, it can be viewed as applying a representation of a continuation to an integer to give another integer. The reason for using the name exec in our setting will become clear shortly.

Our aim now is to define a new semantics, eval”, that behaves in the same way as our previous semantics eval’, except that it uses values of type CONT rather than continuations of type Cont. That is, we seek to define a function:

The desired behaviour of eval” is captured by the following equation:

(2) \begin{eqnarray} {\mathit{eval''}\;\mathit{e}\;\mathit{c}} &=& {\mathit{eval'}\;\mathit{e}\;(\mathit{exec}\;\mathit{c})} \end{eqnarray}

That is, applying eval” to an expression and the representation of a continuation should give the same result applying eval’ to the expression and the continuation it represents.

As previously, to calculate the definition for eval” we proceed by structural induction on the expression e. The base case e=Val n is straightforward,

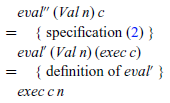
while the inductive case, e=Add x y, uses the definition of exec to transform the term being manipulated to allow an induction hypothesis to be applied:

However, the definition for exec still refers to the previous semantics eval’, via its use of the combinator next. We can calculate a new definition for exec that refers to our new semantics eval” instead by simple case analysis on the CONT argument (no induction required), which proceeds for the three possible forms of this argument as follows:

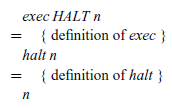
and

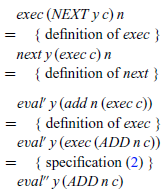
and

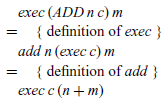
Finally, our original semantics eval for expressions can be recovered from our new semantics eval” by means of the following calculation:

In summary, we have calculated the following new definitions:

Together with the CONT type, these definitions form an abstract machine for evaluating expressions. In particular, the four components can be understood as follows:

• CONT is the type of control stacks for the machine and comprises instructions that determine how the machine should continue after evaluating the current expression. As a result, this kind of machine is sometimes called an ‘eval/continue’ machine. The type of control stacks could also be refactored as a list of instructions:

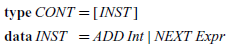
However, we prefer the original definition as it arose in a systematic way and only requires the declaration of a single new type rather than two new types.

• • eval evaluates an expression to give an integer, by simply invoking eval” with the given expression and the empty control stack HALT.

• • eval” evaluates an expression in the context of a control stack. If the expression is an integer value, we execute the control stack using this integer as an argument. If the expression is an addition, we evaluate the first argument x, placing the instruction NEXT y on top of the control stack to indicate that the second argument y should be evaluated once evaluation of the first argument is completed.

• • exec executes a control stack in the context of an integer argument. If the stack is empty, represented by the instruction HALT, we return the integer argument as the result of the execution. If the top of the stack is an instruction NEXT y, we evaluate the expression y, placing the instruction ADD n on top of the remaining stack to indicate that the current integer argument n should be added together with the result of evaluating y once this is completed. Finally, if the top of the stack is an instruction ADD n, evaluation of the two arguments of an addition is complete, and we execute the remaining control stack in the context of the sum of resulting integers.

Note that eval” and exec are mutually recursive, which corresponds to the machine having two modes of operation, depending on whether it is currently being driven by the structure of the expression or the control stack. For example, for $1+2$ we have

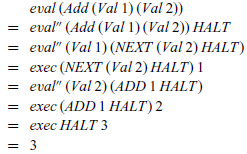
In summary, we have shown how to calculate an abstract machine for evaluating arithmetic expressions, with all of the implementation machinery falling naturally out of the calculation process. In particular, we required no prior knowledge of the implementation ideas, as these were systematically discovered during the calculation.

We conclude by noting that the form of control stacks used in the abstract machine is very similar to the form of contexts used in the contextual semantics in Section 6. Indeed, if we write the type of control stacks as regular algebraic datatype,

and write the type of evaluation contexts that specify the usual left-to-right evaluation order for addition from the end of Section 6 in the same style,

then we see that the two types are isomorphic, i.e. there is a one one-to-one correspondence between their values. In particular, the isomorphism is given by simply renaming the corresponding constructors and swapping the argument order in the case of NEXT and AddL. This isomorphism, which demonstrates that evaluation contexts are just defunctionalised continuations, is not specific to this particular example and illustrates a deep semantic connection that has been explored in a number of articles cited below.

Further reading. Reynolds’ seminal paper (1972) introduced three key techniques: definitional interpreters, continuation-passing style and defunctionalisation. Danvy and his collaborators later showed how Reynolds’ paper actually contained a blueprint for deriving abstract machines from evaluators (Ager et al., 2003a ) and went on to produce a series of influential papers on a range of related topics, including deriving compilers from evaluators (Ager et al., 2003b ), deriving abstract machines from small-step semantics (Danvy & Nielsen, 2004) and dualising defunctionalisation (Danvy & Millikin, 2009); additional references can be found in Danvy’s invited paper (2008). Using the idea of dissecting a datatype McBride (2008) developed a generic recipe that turns a denotational semantics expressed using a fold operator into an equivalent abstract machine.

This section is based upon (Hutton & Wright, 2006; Hutton & Bahr, 2016), which also show how to calculate machines for extended versions of the expression language and how the two transformation steps can be fused into a single step. Similar techniques can be used to calculate compilers for stack (Bahr & Hutton, 2015) and register machines (Hutton & Bahr, 2017; Bahr & Hutton, 2020), as well as typed (Pickard & Hutton, 2021), non-terminating (Bahr & Hutton, 2022) and concurrent (Bahr & Hutton, 2023) languages.

9 Summary and conclusion

In this article, we have shown how a range of semantic concepts can be presented in a simple manner using the language of integers and addition. We have considered various semantic approaches, how induction principles can be used to reason about semantics and how semantics can be transformed into implementations. In each case, using a minimal language allowed us to present the ideas in a clear and concise manner, by avoiding the additional complexity that comes from considering more sophisticated languages.

Of course, using a simple language also has limitations. For example, it may not be sufficient to illustrate the differences between semantic approaches. As a case in point, when we presented the big-step semantics for arithmetic expressions, we found that it was essentially the same as the denotational semantics, except that it was formulated using inference rules rather than equations. Moreover, a simple language by its very nature does not raise semantic questions and challenges that arise with more complex languages. For example, features such as mutable state, variable binding and concurrency are particularly interesting from a semantic point of view, especially when used in combination.

For readers interested in learning more about semantics, there are many excellent textbooks such as (Winskel, 1993; Reynolds, 1998; Pierce, 2002; Harper, 2016), summer schools including the Oregon Programming Languages Summer School (OPLSS, 2023) and the Midlands Graduate School (MGS, 2022) and numerous online resources. We hope that our simple language provides others with a useful gateway and tool for exploring further aspects of programming language semantics. In this setting, it is easy as 1,2,3.