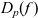Contents
Research Article
Is sized typing for Coq practical?
-
- Published online by Cambridge University Press:
- 24 January 2023, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functional Pearl
Folding left and right matters: Direct style, accumulators, and continuations
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
Fold-unfold lemmas for reasoning about recursive programs using the Coq proof assistant – ERRATUM
-
- Published online by Cambridge University Press:
- 06 March 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
Classical (co)recursion: Mechanics
-
- Published online by Cambridge University Press:
- 04 April 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Read/write factorizable programs
-
- Published online by Cambridge University Press:
- 08 June 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PhD Abstracts
PhD Abstracts
- Part of:
-
- Published online by Cambridge University Press:
- 24 July 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
Normalization by evaluation for modal dependent type theory
-
- Published online by Cambridge University Press:
- 02 October 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A type-directed, dictionary-passing translation of method overloading and structural subtyping in Featherweight Generic Go
-
- Published online by Cambridge University Press:
- 09 October 2023, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tutorial Paper
Programming language semantics: It’s easy as 1,2,3
- Part of:
-
- Published online by Cambridge University Press:
- 26 October 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
Contract lenses: Reasoning about bidirectional programs via calculation
-
- Published online by Cambridge University Press:
- 06 November 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functional Pearl
A correct-by-construction conversion from lambda calculus to combinatory logic
- Part of:
-
- Published online by Cambridge University Press:
- 22 November 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Certified, total serialisers with an application to Huffman encoding
- Part of:
-
- Published online by Cambridge University Press:
- 12 December 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
Level-p-complexity of Boolean functions using thinning, memoization, and polynomials
-
- Published online by Cambridge University Press:
- 12 December 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trace contracts
-
- Published online by Cambridge University Press:
- 13 December 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PhD Abstracts
PhD Abstracts
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation