Hydraulics of subglacial outburst floods: new insights from the Spring–Hutter formulation

Abstract

Using a slightly modified form of the Spring–Hutter equations, glacial outburst floods are simulated from three classic sites, “Hazard Lake”, Yukon, Canada, Summit Lake, British Columbia, Canada, and Grímsvötn, Iceland, in order to calibrate the hydraulic roughness associated with subglacial conduits. Previous work has suggested that the Manning roughness of the conduits is remarkably high, but the new calibration yields substantially lower values that are representative of those for natural streams and rivers. The discrepancy can be traced to a poor assumption about the effectiveness of heat transfer at the conduit walls. The simulations reveal behaviour that cannot be inferred from simplified theories: (1) During flood onset, water pressure over much of the conduit can exceed the confining pressure of surrounding ice. (2) Local values of fluid potential gradient can differ substantially from the value averaged over the length of the conduit, contradicting an assumption of simple theories. (3) As the flood progresses, the location of flow constrictions that effectively control the flood magnitude can jump rapidly over large distances. (4) Predicted water temperature at the conduit outlet exceeds that suggested by measurements of exit water temperature.

Notation

Introduction

Röthlisberger (1972) and Shreve (1972) were the first to describe the physics of steady water flow through ice-walled conduits of circular cross-section. Although these theories, identical in their essence, have been instrumental in shaping understanding of the subglacial water system, the assumption of steady flow imposes serious limitations. For valley glaciers, which are subjected to strong diurnal meltwater forcing during the summer months, the theory cannot explain many observed features of subglacial water-pressure records. For glacier outburst floods, or “jökulhlaups”, which result from the unstable growth of one or more englacial or subglacial meltwater conduits that tap a reservoir of stored water, the steady-flow assumption is impossibly restrictive. Mathews (1973) and Björnsson (1974) addressed this short-coming and identified the essential physics of subglacial out-burst floods, laying the foundation for a landmark paper by Nye (1976). In the Nye theory the effects of lake temperature are ignored and several untested assumptions are made: a simplified form of heat transfer is postulated and water flow is assumed to be driven by the fluid potential gradient averaged over the length of the conduit. Clarke (1982) modified the Nye theory to account for the effects of lake temperature and reservoir geometry and used the extended theory to simulate discharge hydrographs for a variety of ancient and modern floods (Clarke and Mathews, 1981; Clarke, 1982; Clarke and others, 1984). A key assumption of the papers by Clarke and co-authors is that outburst floods are controlled by conditions at a single point along the conduit, a “seal” which acts as a flow-restricting bottleneck and must be located sufficiently close to the reservoir that the water temperature is effectively that of the reservoir. Björnsson (1992) used this theory to obtain simulated hydrographs for a number of Icelandic outburst floods and found that the approach “yields moderately good simulations for jökulhlaups from Grímsvötn”, Iceland. For many cases the bottleneck assumption seems plausible, but it is easy to imagine situations where it is suspect. A leading objective of the present contribution is to assess the validity of bottleneck models.

Rather than resort to simplifying assumptions about the existence and location of a flow bottleneck, Spring (1980) and Spring and Hutter (1981, 1982) developed a complete mathematical description of the temporally evolving water velocity, discharge, temperature and cross-sectional area over the entire length of the conduit. Although their formulation is impressively complete, close reading of Spring (1980) and Spring and Hutter (1981) makes it clear that efforts to obtain numerical solutions of the full system of equations met with limited success and the authors were obliged to make major simplifying assumptions in order to obtain results. Their statement that the “numerical solution … required long computing times” (Spring and Hutter, 1981) strongly suggests that numerical stiffness was the underlying source of difficulty.

Recent work on outburst flood hydraulics has followed divergent paths. Walder and Costa (1996) focused on the hazard aspect and considered a breach drainage release mechanism. Fowler and Ng (1996) and Ng (1998) introduced a substantial innovation by considering the flood conduit to be floored by deformable sediment, and Fowler (1999) concentrated attention on the conditions for flood release from the Grímsvötn reservoir. Raymond and Nolan (2000) developed a new theory, analogous to that of Nye and Clarke, to describe outburst floods by overtopping of the ice dam. Copious references on outburst flooding can be found in a comprehensive review byTweed and Russell (1999).

Model

Geometry and water balance

The geometry of the outburst flood model is summarized in Figure 1. I assume a Cartesian coordinate system with x and y corresponding to easting and northing coordinates relative to some arbitrary geographical origin and z as the vertical distance above some elevation datum (e.g. sea level).The elevation of the bed surface is Z _b(x, y) and that of the glacier surface is Z _i(x, y). A lake with water level Z _w(t) is impounded by the glacier, and A(Z _w) is the lake area as a function of elevation (which I shall refer to as the hypsometric function). A spatially fixed drainage path, passing through or beneath the glacier, is assumed to connect the conduit inlet to a subaerial outlet. Downflow distance along this path is denoted s, where s = 0 at the inlet and s = l ₀ at the outlet. The geographical coordinates of the drainage path are described by the three functions [X _k(s), Y _k(s), Z _k(s)]. In practice, the path is determined by specifying a table of N values for the triplets [X _k] _j , [Y _k] _j and [Z _k] _j , where j = 1…N and the functions X _k(s), Y _k(s) and Z _k(s) are generated by piecewise-linear interpolation. I have confirmed that the modelling results are not greatly affected by the spatial sampling interval along the flow path, provided that the major topographic features are satisfactorily resolved. Although the path end-points at [[X _k]₁, [Y _k]₁, [Z _k]₁] and [[X _k] _N , [Y _k] _N , [Z _k] _N ] are part of the initial specification, the path length l ₀ must be calculated after-the-fact by numerical integration over s, e.g. by summation over

(1)

If Z _k = Z _b the path is subglacial, but this is not an essential requirement. For the models considered in this study, the drainage routing will be assumed to follow a straight line connecting the map positions of the inlet and outlet; thus only contribution to conduit tortuosity is from elevation excursions along the path.

Fig. 1. Model geometry. (a) Schematic diagram of the bed topography, glacier and ice-dammed lake.The conduit is indicated by a dashed line and follows a partly subglacial and partly englacial route.The seal is assumed to be located at the point of maximum ice thickness. (b) An ice-walled conduit having circular cross-section. (c) An ice-roofed and bed-floored conduit having semicircular cross-section.

Until recently, most theoretical treatments of subglacial conduits have followed the assumption of Röthlisberger (1972) and Shreve (1972) that conduits have a circular cross-section. Hooke and others (1990) proposed a modification of the Röthlisberger theory to allow for non-circular channels having a small height/width aspect ratio. Ng (1998) developed this idea in greater detail and employed it in his outburst flood model, but calculating the creep closure rate of wide channels is not straightforward. In the present work, the conduit is assumed to have two possible cross-sectional geometries, circular or semicircular, so that for a water-saturated conduit the wetted perimeter and cross-sectional area are given by

(2)

(3)

where R is the conduit radius.The hydraulic radius, defined as the ratio of the channel cross-sectional area to the wetted perimeter, is

(4)

For subsequent use, I shall also define the “melting perimeter” of the conduit as that part of the conduit perimeter that is ice-walled and subject to melting:

(5)

Water level in the lake is determined by a balance of inflow Q _in from the surrounding environment and discharge Q through the drainage conduit so that

(6)

When Q _in > Q the level rises, either indefinitely or until an alternative drainage path is encountered; the elevation of this spillway is denoted Z _spill. If Q _in < Q the water level falls and, if it reaches the elevationof the conduit inlet Z _k(0), drainage through the conduit becomes supply-limited and Q = Q _in.

Hydraulics and thermodynamics

The model of Spring and Hutter is described in a thesis by Spring (1980) and two research papers (Spring and Hutter 1981, 1982). Regrettably the thesis and Spring and Hutter (1981) contain typographical errors that can only be clarified by referring to the lengthy and challenging paper by Spring and Hutter (1982). Rather than retrace this work I shall summarize its essence, making some minor notational changes and adding several new features. Written as state evolution equations, the balance equations for water mass, ice mass, linear momentum and internal energy are respectively

(7)

(8)

(9)

(10)

where

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

The foregoing system of equations can be readily solved using the numerical method of lines (e.g. Schiesser, 1991) and I shall gladly provide MATLAB scripts to anyone interested in extending this work. Justifications for Equations (7) and (8) are presented in Appendix A, and those for Equations (15) and (20) are in Appendix B. Note that in the notation for Darcy–Weisbach and Manning roughness I have attempted to be explicit about the roughness of a single material (e.g. f _R), the roughness of particular materials such as ice and bed (e.g. f _i and f _b) and the perimeter-averaged roughness for a conduit walled by several different materials (e.g. 〈f _R〉).

Equation (7) differs in a crucial way from the corresponding expression used by Spring (1980) and Spring and Hutter (1981, 1982)

(21)

In their formulation, the interaction of Equations (8) and (21) gave rise to the problem of numerical stiffness which plagued their modelling efforts. Replacing Equation (21) by Equation (7) is the key step that renders the numerical system tractable. In effect, this transformation allows the fluid to be slightly compressible and reduces numerical stiffness (Appendix A). Although I use physical reasoning to justify the introduction of the parameter β into the Spring–Hutter equations, the results are insensitive to the assigned value of β over several orders of magnitude and it can be properly regarded as a parameter of the numerical analysis rather than a genuine physical constant. Whereas the tabulated compressibility of water is β = 4.5 × 10⁻¹⁰ Pa⁻¹, I have found that setting β = 10⁻⁷ Pa⁻¹ yields much faster integrations with no apparent effect on the results.

Together Equations (7) and (8) imply that the conduit is water-saturated over its entire length and throughout the time interval of interest. Clearly this cannot be the case in the final moments of floods that terminate by complete drainage of their reservoir. Even during the flood, openchannel flow conditions may develop near the tunnel exit so that for modelling purposes the effective conduit length l ₀ is somewhat less than the path length from the lake to the exit point. However, the length discrepancy is expected to be small and unlikely to have a noticeable effect on the simulation results. Equation (8) governing conduit growth is based on simplifying assumptions that do not have general validity. When effective pressure is negative (water pressure exceeds the ice overburden pressure) it is assumed that creep processes enlarge the conduit. This is the simplest assumption because it assumes there is no exchange of water between the conduit and its surroundings, but it eliminates the possibility of water leaking from the conduit to join a subglacial or englacial drainage network. Unusual outburst phenomena such as the propagation of subglacial flood waves and explosive release of water (Jóhannesson, 2002; Björnsson, 2003) strongly suggest that flood water can be distributed areally over the bed rather than confined to a simple conduit. A further assumption associated with Equation (8) is that the conduit geometry does not change with time so that, for example, an initially semicircular conduit remains semicircular. Simplicity is the only justification for this assumption.

Ng (1998) covers similar ground but makes different assumptions in solving a system of equations comparable to Equations (21), (8), (9) and (10). A scaling analysis is employed to simplify the equations which are then solved using a time-stepping finite-difference method. It is possible that our two approaches would lead to essentially identical results, but our aims differ and it is not possible to confirm this point.

Initial conditions

The initial conditions for the simulation are taken as Z _w(0) = Z _init, T _w(s, 0) = −c _T ρ _i g[ Z _i(s) − Z _k(s)] (water temperature is at the pressure-melting point), S(s, 0) = S _init (constant over the entire length of the initial leakage path),φ(s, 0) = ρ _w g [Z _w(0) − s Z _w(0) − Z _k(l ₀)]l ₀], p _w(s,.0) = φ(s, 0) − ρ _w gZ _k(s) and

(22)

The boundary conditions are T _w(0, t) = T _lake and p _w(l ₀ , t) = 0 with a boundary condition at p _w(0, t) enforced by assuming ∂p _w(0, t) = ∂t = ρ _w gdZ _w/dt. Although the initial conditions on v, p _w and T _w are only rough approximations, the main issue in choosing initial conditions is to provide an acceptably smooth launch for the numerical integration. Poorly chosen initial conditions will cause the integrator to fail, but any reasonable assignment that avoids this outcome is acceptable because the system quickly loses any memory of a rough start. Note that by assuming the existence of an initial leakage path (S(s, 0) = S _init) Iavoidthe interesting but complicated issue of how the flood is initiated. However, it is not necessarily the case that a small initial conduit will enlarge with time and produce an outburst flood; a conduit that cannot be sustained will slowly seal itself.

Recalibration of Flow Resistance

In this section, I apply the modified Spring–Hutter formulation to the problem of simulating outburst floods for the comparatively well-studied cases of “Hazard Lake”, Yukon, Canada, Summit Lake, British Columbia, Canada, and the Grímsvötn reservoir within Vatnajökull ice cap in Iceland. The common physical constants of the models are given in Table 1, and model-specific parameters of the three reference models are listed in Table 2.

Table 1. Physical constants

Table 2. Parameters for reference models

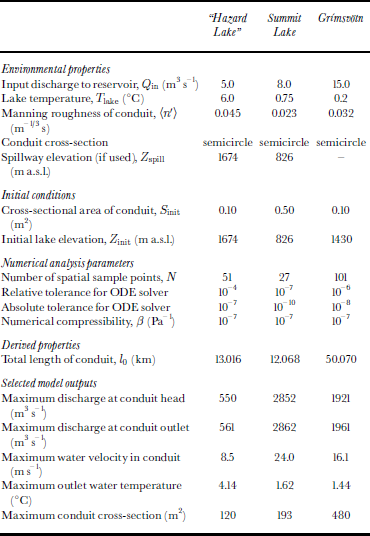
The question of whether to adopt the Manning or the Darcy–Weisbach roughness description is not a major issue for most natural flows because the range of discharge for a given river or conduit is unlikely to vary over many orders of magnitude. For outburst floods, however, the decision is important. The relationships between the two descriptions are

(23)

(24)

and from Equation (23) it is clear that for an assumed constant value of f _R the Manning roughness increases as the hydraulic radius increases. Thus the predicted roughness of large conduits is greater than that for small conduits. Hydrologists claim the opposite and would, in fact, assert that even when a constant Manning roughness is assumed (which according to Equation (24) would lead to decreasing Darcy–Weisbach roughness with increasing hydraulic radius) the roughness for large conduits and for high discharge rates is overestimated (e.g. Dingman,1984, p.145). A desirable characteristic of the roughness description is that numerical values of the roughness parameterization do not vary with the scale of the flood. Although neither description satisfies this requirement, the Manning description comes closer to this ideal and is therefore my preferred choice.

“Hazard Lake” flood models

The 1978 flood from glacier-dammed “Hazard Lake” is among the best-studied outbursts and motivated the development of a bottleneck model (Clarke, 1982) based on a modification of Nye’s theory (Nye, 1976). The geometry of the reservoir is very well determined and the geometry of the 13 km flood path through or beneath Steele Glacier is reasonably well constrained. Figure 2a shows the measured hypsometric function (Clarke, 1982, table 2) for the lake, and Figure 2b summarizes the assumed geometry of the ice surface, bed topography and subglacial flood path (ABC). The elevation of the lake surface and outlet (C) correspond to measured values, as does the distance between the inlet (A) and outlet. The representation of the ice surface for Steele Glacier is taken to be simple but consistent with the 1978 ice topography. There are no measurements of ice thickness, so I have taken the elevation of the seal (B) and the ice thickness above the seal to correspond to those assumed in Clarke (1982). Lake temperature was not measured in 1978, so water temperature measurements taken in summer 1979 were substituted. The discharge hydrograph for the 1978 flood was calculated by numerical differentiation of the record of lake level vs time and then applying the known hypsometric function of the lake. From the calculated hydrograph, the maximum flood discharge was estimated to be approximately 640 m³ s⁻¹.

Fig. 2. Geometry and discharge for “Hazard Lake” outburst floods. (a) Hypsometric function for lake (Clarke, 1982). (b) Geometry of glacier and subglacial flood routing. (c) Simulated discharge hydrographs. Curve A uses the model and parameters of Clarke (1982), and the remaining curves are simulated using the present model and data from Tables 1 and 2 (except when otherwise indicated). Curve B is for a circular conduit with Manning roughness of n^′ = 0.06 m^−1/3 s; curve C is for a semicircular conduit having a perimeter-averaged Manning roughness of 〈n^′〉 = 0.045 m^−1/3 s and corresponds to the reference model of Table 2; curve D is for a circular conduit and Darcy–Weisbach roughness of f_R = 0.20; curve E is for a semicircular conduit and perimeter-averaged Darcy–Weisbach roughness of 〈f_R〉 = 0.12.The curves have been time-shifted relative to each other in order to improve their clarity.The slope discontinuity at peak discharge occurs because the flood is terminated by complete drainage of the lake.

Figure 2c shows simulated discharge hydrographs for the 1978 flood. Curve A is the hydrograph calculated in Clarke (1982) using the bottleneck model and parameters listed in Clarke (1982, table 3); the Manning roughness for this model is n ^′ = 0.105 m^−1/3 s and the conduit geometry is circular. The remaining curves were calculated using the Spring–Hutter model as described in the previous section. Curve B is for a circular conduit having a Manning roughness of n ^′ = 0.06 m^−1/3 s, while curve C corresponds to the “Hazard” reference model of Table 2 and is for a semicircular conduit with a perimeter-averaged Manning roughness of 〈n ^′〉 = 0.045 m^−1/3 s. (I use angular brackets to draw attention to the fact that the Manning roughness represents a perimeter-averaged value that allows for differing roughnesses of ice and bed. For a circular ice-walled conduit the perimeter-averaged roughness and the conventional Manning roughness n ^′ are identical.) Similarly, curves D and E are for a circular conduit with Darcy–Weisbach roughness f _R = 0.20 and a semicircular conduit with perimeter-averaged Darcy–Weisbach roughness 〈f _R〉 = 0.12, respectively. Despite differences in the modelling assumptions, all the curves are essentially identical. The assumed Manning roughness for the bottleneck model (A) is greater than that for the corresponding Spring–Hutter model (B), and models that assume a semicircular conduit require less flow resistance than those that assume a circular conduit. Although I have expressed a preference for the Manning roughness description, both the Darcy–Weisbach and Manning descriptions are capable of providing visually acceptable hydrographs.

Summit Lake flood model

Figure 3 presents the geometrical assumptions and discharge hydrographs for the model of the 1967 outburst flood from Summit Lake. The hypsometric data (Fig. 3a) are from Clarke and Mathews (1981, table 1), and the assumed glacier geometry (Fig. 3b) is consistent with topographic maps and seismic soundings by Doell (1963). Water discharge into the lake was estimated as Q _in = 8 m³ s⁻¹ (Clarke and Mathews, 1981, p.1456). Lake temperature, measured in 1968, was taken to be 0.75°C (Gilbert, 1969). Discharge hydrographs are presented in Figure 3c. Curve A corresponds to the hydrograph obtained by Clarke and Mathews (1981) using a bottleneck model and closely matches the observed hydrograph (see Clarke and Mathews, 1981, fig. 3). Curve B presents the results of a Spring–Hutter simulation using the geometric data of Figure 3 and other data from Tables 1 and 2. Although the two curves are virtually identical, the assumed values of Manning roughness differ substantially, being n ^′ = 0.12 m^−1/3 s for the bottleneck model and 〈n ^′〉 = 0.023 m^−1/3 s in the present study. Rather than being surprisingly high, as for the bottleneck model, the flow resistance for the Spring–Hutter model is surprisingly low, though not unacceptably low. Instead of assuming a low value for 〈n ^′〉 it would be possible to accept a larger value and postulate that the lake temperature exceeded the assumed value of 0.75°C.

Fig. 3. Geometry and discharge for Summit Lake outburst floods. (a) Hypsometric function for lake (Clarke and Mathews, 1981, table 1). (b) Assumed geometry of glacier and subglacial flood routing. (c) Smooth curve that closely fits the observed discharge hydrograph (A) compared to simulated hydrograph (B). The slope discontinuity at peak discharge occurs because the flood is terminated by complete drainage of the lake.

Grímsvötn flood model

Outburst floods from Grímsvötn have been the most influential in terms of their stimulus to science and prompted the seminal contributions of Björnsson (1974, 1988) and Nye (1976). I shall take the 1986 outburst flood as the reference flood for Grímsvötn. Though one of the lesser floods, it is well constrained by observations. Figure 4a and b summarize the geometrical data for the lake (Björnsson, 1992, fig. 2), glacier and subglacial routing (Björnsson, 2003, fig. 8). Other model input data are given inTables 1 and 2. The lake temperature, taken to be 0.2°C, is based on 1991 measurements (Björnsson, 1992, p.102), and the water input to the reservoir is Q _in = 15 m³ s⁻¹, consistent with estimates by Björnsson (1988, p.78).

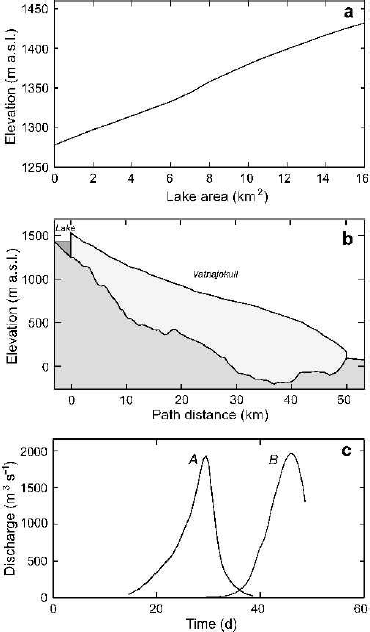
Fig. 4. Geometry and discharge for Grímsvötn 1986 outburst flood. (a) Hypsometric function for lake (Björnsson, 1992, fig. 2). (b) Geometry of glacier and subglacial flood routing (Björnsson, 1974, fig. 14). (c) Observed (A) and simulated (B) discharge hydrographs.The flood is terminated by complete drainage of the reservoir.

Discharge hydrographs are presented in Figure 4c. Curve A corresponds to the observed hydrograph (Björnsson,1992, fig. 4) and curve B to the hydrograph simulated using the Spring–Hutter model. A semicircular conduit having a perimeter-averaged Manning roughness of 〈n ^′〉 = 0.032 m^−1/3 s was assumed. Björnsson (1992, fig. 9) used a bottleneck model to calculate a similar hydrograph but assumed a roughness of n ^′ = 0.08 m^−1/3 s.

Results

A common feature of the recalibrated flood models for “Hazard Lake”, Summit Lake and Grímsvötn is that reasonable fits between simulated and observed hydrographs can only be obtained if one assumes that the flow resistance is substantially lower than that used for bottleneck models. In part this can be explained by the assumption of a semicircular rock-floored conduit, but even if a circular ice-walled conduit is assumed it is necessary to accept lower values of flow resistance than for bottleneck models. It can be shown that the significant discrepancy between earlier work and the present study results from shortcomings of the Nye (1976) postulate concerning the effectiveness of heat transfer from the conduit to the ice walls (Appendix C). To my knowledge, the Nye postulate has not previously been tested and the apparent failure of this postulate is an important new result. In this section I shall examine additional features of the recalibrated reference models and expose some short-comings of bottleneck models. Note that in all cases t = 0 days signifies the time at which plotting begins. The actual simulations began at substantially earlier times, but the plots focus on the flood itself rather than the slow onset.

Thermal evolution and exit temperature of water

Figure 5 summarizes the spatial and temporal evolution of water temperature for the three reference floods. Temperature curves (labelled lines and left abscissa) are presented for nominal down-flow distances of 0 (the conduit inlet), 0.2l ₀, 0.4l ₀, 0.6l ₀, 0.8l ₀ and l ₀ (the conduit outlet); discharge hydrographs (dashed curves and right abscissa) are included for reference. Note that the time axis has been arbitrarily shifted so that t = 0 days does not necessarily correspond to the start time for the simulation. Initially the growth of the drainage conduit is extremely slow and, although the magnitude of discharge through the small initial leakage path is small, it is nevertheless sufficient to affect the water temperature in the conduit.

Fig. 5. Temporal and spatial evolution of water temperature for outburst flood simulations. Simulated discharge hydrographs (dashed lines) are included for reference. Labelled curves correspond to different down-flow distances relative to the length l₀ of the flood path so that 0 corresponds to the conduit inlet and 1 to the outlet. Time zero represents the time at which plotting is initiated but not the actual time at which the simulation was begun. (a) “Hazard Lake” outburst. (b) Summit Lake outburst. (c) Grímsvötn outburst.

Figure 5a shows results for the “Hazard Lake” outburst. Lake temperature was taken to be 6.0°C (Table 2), so the curve for s = 0 does not vary from this value. Near t = 0 days the temperature at s = 0.2l ₀ already reflects the influx of warm lake water and has risen from its initial temperature (taken as the pressure-melting temperature of ice) to around 3°C. As the flood progresses, the influence of warm water from the lake is projected farther down the conduit, and at the flood peak the temperature of water exiting the conduit is 4.1°C, indicating that at this stage of the flood the advective transport of heat greatly exceeds the loss by melting of the conduit walls.

In contrast, the Summit Lake outburst simulation (Fig. 5b) illustrates the effects of a comparatively cold water reservoir. The lake temperature is 0.75°C as indicated by the curve for s = 0. At t = 0 days the water temperature at s = 0.2 l ₀ is substantially colder than the lake but nonetheless above the melting temperature of ice. Farther down-flow the temperatures are below 0°C but above or near the pressure-melting temperature at these locations. As the flood progresses, the temperature along the conduit increases until at around 2.5 days the water temperature in the conduit everywhere exceeds the lake temperature. This additional warming is caused by viscous dissipation in the conduit. At this stage of the flood, the water temperature increases with down-flow distance, the exact opposite of the situation for the “Hazard Lake” flood. The maximum water temperature during the flood occurs at the conduit exit and equals 1.6°C, substantially above the lake temperature.

The Grímsvötn outburst simulation (Fig. 5c) has clear similarities with that for Summit Lake, although the temperature curves have more character. Again the lake temperature is only slightly above the melting temperature, and viscous dissipation is important in enabling the flood to develop. By t = 6 days the water temperature in the drainage conduit is everywhere above the lake temperature even though the flood is only beginning to enter its rapid growth phase. As with the simulated outburst for Summit Lake, maximum water temperature occurs at the conduit outlet. The predicted maximum water temperature is 1.4°C, in contrast to the assumed lake temperature of 0.2°C. In fact such a high outlet temperature has not been observed and this suggests some shortcomings that I shall discuss subsequently.

Evolution of fluid potential gradient and effective pressure

The Spring–Hutter model permits detailed examination of the evolution of water pressure and potential energy gradient as an outburst flood progresses. Of special interest is the spatial position of flow constrictions in the drainage conduit and whether these constrictions remain fixed in space or migrate as the flood progresses. A fundamental assumption ofthe Nye model is that the fluid potential gradient ∂ϕ/∂s is reasonably well approximated by its length-averaged value 〈∂ϕ/∂s〉, whereas a fundamental assumption of bottleneck models is that the seal is the dominant flow constriction at all stages of an outburst flood. These assumptions cannot be tested without resorting to a more comprehensive model such as that of Spring and Hutter. To test the Nye assumption and to identify regions of flow constriction, I evaluate the spatial gradient of the hydraulic potential ϕ = p _w + ρ _w gZ _k and seek regions where −∂ϕ/∂s is greatest or, equivalently, where ∂ϕ/∂s is least. Letting s ^* denote the instantaneous value of s at which −∂ϕ/∂s is maximum, one can plot s ^*(t); and this locates the down-flow position of the bottleneck as the flood progresses. A more detailed picture of flow constrictions is obtained by plotting ∂ϕ(s, t)/∂s over the course of the flood. For the Nye assumption to be valid, the potential energy gradient should vary with time but not with distance along the conduit. A second matter of interest is the effective pressure p _e = p _i − p _w, which is diagnostic of whether water pressure exceeds the ice flotation pressure. As shall be shown, the water pressure in the conduit can greatly exceed the ice overburden pressure, and this has implications for the dispersal of water along the ice–bed interface, hydraulic fracturing of the ice walls and the escape of water by artesian outflow to the glacier surface.

“Hazard Lake” model results

Figure 6 shows the temporal evolution of fluid potential gradient and effective pressure for the “Hazard Lake” reference model. The spatial location of the dominant flow constriction (dashed line and right abscissa) and the flood hydrograph (solid line and left abscissa) are plotted in Figure 6a. Interestingly, the flow constriction is located at the glacier terminus (s ^* = 13 km) throughout the observation interval, and at no time is the flow constriction located at the “seal” defined by the maximum ice thickness (s _seal = 1 km in Fig. 2b). Apparentlythe sensible heatof lake water is sufficient to overcome flow constrictions near the inlet and it is the lower temperature of water near the glacier terminus that maintains a constriction at the outlet. Although the seal may have played a role in controlling the onset of the flood, it does not serve as the controlling flow constriction once the flood has started to develop.

Fig. 6 Temporal and spatial evolution of effective pressure and flow constriction for “Hazard Lake”outburst simulation. (a) Simulated discharge hydrograph (solid line and left abscissa) and down-flow distance of the flow “bottleneck”as a function of time (dashed line and right abscissa). (b) Spatio-temporal evolution of fluid potential gradient ∂φ(s, t) = ∂s. Contours are not labelled, but dark shading corresponds to regions where potential energy dissipation is concentrated, hence regions where flow is restricted. (c) Spatio-temporal evolution of effective pressure p_e(s, t) in conduit. Negative values of effective pressure correspond to water pressures exceeding the ice flotation pressure. (Contours are in units of MPa.)

Figure 6b shows the pattern of fluid potential gradient associated with the “Hazard Lake” outburst simulation. The contours have not been labelled because it is the pattern, rather than the actual magnitudes, that commands interest. Dark shading corresponds to regions where potential energy dissipation is concentrated, and it is clear that this is greatest in the lower reaches of the drainage conduit and decreases monotonically toward the lake. The fact that the fluid potential gradient varies spatially as well as temporally indicates that the Nye assumption is not satisfied. The putative “seal” at s _seal = 1 km seems irrelevant to this pattern.

The simulated distribution of effective pressure during the “Hazard Lake” outburst is given in Figure 6c with contours labelled in MPa. The 0 MPa contour separates the region of ice flotation (negative effective pressure) from that where ice pressure exceeds water pressure. Note that water pressure exceeds the ice flotation pressure over virtually the entire length of the conduit for the entire observation interval and that, over the middle section of the conduit, water pressure exceeds ice overburden pressure by at least 1 MPa for the first 2.3 days of the observation window. When reckoned in terms of the equivalent water level, this corresponds to a water column >100 m above the flotation level and would be sufficient to drive water to the surface of Steele Glacier if cracks or other water paths existed.

Summit Lake model results

A similar analysis of the Summit Lake outburst simulation produces a more interesting story (Fig. 7). Figure 7a shows the position of the dominant flow constriction as a function of time (dashed line and right abscissa) with the flood hydrograph included for reference (solid line and left abscissa). During the early development of the flood the flow constriction is located at the glacier terminus (s ^* = 12 km in Fig. 3b), but at around t = 2.5 days the constriction migrates up-glacier, first in a regular fashion but then in a discontinuous jump from s* ≈ 8 km to the conduit inlet at s ^* = 0 km. The up-flow migration of the flow constriction appears to be associated with the evolving thermal conditions in the drainage conduit (Fig. 5b). At around t = 2.5 days the water temperature at the conduit exit begins to exceed the lake temperature so that concentrated viscous dissipation near the conduit exit is no longer required to overcome creep closure by ice pressure.

Fig. 7. Same as Figure 6, but for Summit Lake outburst simulation.

Figure 7b shows the pattern of the fluid potential gradient and clarifies the nature of the previously noted jump in s ^*. Dark shading indicates regions where potential energy dissipation is concentrated, and the overplotted dashed line indicates the migration of the flow constriction, as also plotted in Figure 7a. Note that during the early stages of the flood, potential energy dissipation is concentrated in the lower reaches of the conduit, and during the rapid growth phase of the flood the potential energy dissipation is concentrated near the conduit inlet. The jump in s ^* is clearly related to the morphology of the surface ∂φ(s, t)/∂s. As for the “Hazard Lake” simulation, the Nye assumption clearly fails.

Figure 7c shows the distribution of effective pressure in the conduit as the flood progresses. The contours are labelled in MPa and the zero contour is clearly indicated. Water pressure exceeds the ice flotation pressure only in the earliest stages of the flood, and the overpressure never exceeds 0.6 MPa.

Grímsvötn model results

For the Grímsvötn flood simulation the flow constriction shows behaviour similar to that found in the Summit Lake simulation. In the early stages of the flood, the flow constriction is located near, though not at, the conduit outlet (s ^* ≈ 44 km), but, as the flood begins to accelerate, the flow constriction first jumps to the conduit outlet and then at around 5.5 days jumps up-flow to the conduit inlet where it remains until the flood terminates (Fig. 8a). An examination of the contour diagram for ∂φ(s, t)/∂s (Fig. 8b) indicates that the spatial pattern of the fluid potential gradient is complex, presumably because of the complex bed topography assumed for this model (Fig. 4b), and it is evident that the Nye assumption is not satisfied. The effective pressure distribution (Fig. 8c) is also complicated for this model. Superflotation pressures only obtain during the early development of the flood and cease to exist after t = 6.5 days.

Fig. 8. Same as Figure 6, but for Grímsvötn outburst simulation.

Influence of “seal” position on peak discharge

If it could be demonstrated that bottleneck simulations and Spring–Hutter simulations yielded essentially similar results, even if they required different calibrations for flow resistance, one could dispense with the unnecessary complication of the Spring–Hutter model. The following numerical experiments demonstrate that this is not the case. Bottleneck models reduce the geometric description of the flood path to the following essentials: input elevation Z _k (0), output elevation Z _k(l ₀), seal elevation Z _k(s _seal) and ice surface elevation at the seal Z _i(s _seal). There is a further implicit assumption that the seal is near the lake so that s _seal → 0. Figure 9 shows five different glacier geometries that have identical values of Z _k(0), Z _k (l ₀), Z _k(s _seal) and Z _i(s _seal) and differ only in the value of s _seal which varies from 1 km (ice geometry A) to 12 km (ice geometry E) for a 20 km long drainage conduit. For each geometry Z _k(0) = 500 m a.s.l., Z _k(l0) = 0 m a.s.l., Z _k(s _seal) = 0 m a.s.l. and Z _i(s _seal) = 800 m a.s.l. The conduit is assumed to be semicircular with a perimeter-averaged Manning roughness of 〈n ^′〉 = 0.04 m^−1/3 s for all runs. Figure 10 presents a suite of simulated flood hydrographs corresponding to each of the assumed glacier geometries and lake temperatures of 0.5°C (Fig. 10a), 2.0°C (Fig. 10b) and 6.0°C (Fig. 10c). For every case there is a systematic decrease in peak discharge magnitude as the distance between the lake and seal is increased. The effect is most pronounced when the lake temperature is low (Fig. 10a), and least pronounced when it is high (Fig. 10c). Examining Figure 10c, one could argue that the influence of seal location is not sufficiently pronounced to justify the added complexity of Spring–Hutter models, but this is clearly not the case for Figure 10a. Thus, in general, it appears that it is necessary to employ Spring–Hutter modelling before one can decide whether bottleneck models are an acceptable simplification.

Fig. 9. Five simple glacier geometries having identical values for inlet and outlet elevation and ice thickness at the “seal”. For geometry A the location of maximum surface elevation and minimum bed elevation are each labelled A, and similarly for the remaining four geometries. For geometry A the seal is closest to the lake, and for geometry E it is farthest down-flow.

Fig. 10. Effect of water temperature and routing geometry on simulated discharge hydrographs. A–E refer to the subglacial routings associated with glacier illustrated in Figure 9. (a) Lake temperature 0.5°C. (b) Lake temperature 2.0°C. (c) Lake temperature 6.0°C.

Discussion and Conclusions

Much attention could be devoted to the issue of calibrating the flood models, i.e. finding proper assignments of loosely constrained parameters such as the hydraulic roughness of the conduit. In the present work, I have only attempted to seek rough calibrations because the available data do not justify a more ambitious attack. For example, lake temperature data and outburst flood data are rarely collected simultaneously and thus there is an ambiguous association between the assumed value for T _lake and a given outburst flood. Errors in T _lake affect the predicted flood magnitude and thus can give rise to false calibrations of hydraulic roughness. As already mentioned, the temperature of “Hazard Lake” was taken in 1979, whereas the flood was measured in 1978; that for Summit Lake was measured in 1968 but the flood was monitored in 1969; for Grímsvötn the measurements were taken in 1991 and are applied to the 1986 flood. Present models also assume an isothermal lake, whereas reported measurements (e.g. Gilbert, 1969; Björnsson, 1992) indicate that the lakes, unsurprisingly, have a thermal structure which could affect the detailed form of the outburst hydrograph. One hopes that the ongoing study of outburst floods from Hidden Creek Lake, Alaska, U.S.A. (Anderson and others, in press), will yield the comprehensive data that will allow these outstanding problems to be addressed.

The predicted temperature of water exiting the conduit at the flood climax (Fig. 5) is substantially higher than the temperature suggested by observations. For example, Rist (1955) reported a water exit temperature of 0.05°C for the 1954 outburst from Grímsvötn, whereas the reference model for the 1986 outburst (Table 2) predicts a temperature of 1.44°C. Björnsson (1992, p.104) has considered this problem of the models and states:

The actual heat transfer by flowing water during jökulhlaups is more effective than accounted for by Spring and Hutter’s (1981) model for simulation of drainage (as pointed out by Nye (1976)). The empirical heat transfer equation may be wrong at the high Reynolds numbers in the jökulhlaups. On the other hand, melting of ice may not be restricted to the walls, because ice needles, eroded by debris and sand from the walls, mix with the water.

I have explored the consequences of replacing Equation (19) (McAdams, 1954) by alternative expressions (Bird and others, 1960) and found little to distinguish them. If the problem is associated with the heat-transfer empiricism, then existing formulas are either inappropriately used or badly wrong. One possible source of difficulty (personal communication from N. F. Humphrey, 1991) is that conventional heat-transfer formulas, which assume warm water entering a pipe, may not apply to the situation of a fluid heated by viscous dissipation in its frictional boundary layer. This concern warrants further study. Björnsson’s second explanation, that outburst flood waters are a dilute suspension of ice crystals, also strikes me as plausible. This possibility should be vigorously explored, from both an observational and theoretical perspective. It would not be challenging to extend the Spring–Hutter work by adding a balance equation for suspended ice crystals that would include an ice production term associated with mechanical abrasion of the ice walls and a mass-loss term associated with melting of the crystals.

The predicted jumps in bottleneck position (Figs 7 and 8) and the associated rapid rearrangements of conduit pressure are extremely interesting. It is possible that such rapid structural adjustments can produce unexpected features in discharge hydrographs that have been previously attributed to additional phenomena such as tunnel collapse.

Superflotation water pressures are predicted for all three reference models. Excess water pressure would be expected to drive water out of the conduit and along the ice–bed interface, creating the possibility of tapping into pre-existing subglacial drainage paths. An observable consequence of such behaviour would be the formation of more than one drainage outlet for a single flood. Björnsson (1998) notes that for large outbursts from Grímsvötn as many as 10–15 highcapacity drainage tunnels can develop. From this perspective, it is interesting that for all three models the water pressure is highest during the flood onset and decreases as the flood peak is reached. High-capacity outlets can only exist if they are formed early. If water pressure greatly exceeds the ice pressure then an englacial crack system can develop by hydrofracturing. If water pressure (expressed as hydraulic head) exceeds the ice thickness, water can be routed from the drainage conduit to the glacier surface following a system of existing or newly created cracks, as observed for Grímsvötn floods (Björnsson, 1998). Evidence for both ice fracturing and supraglacial water routing is especially well documented for the huge outburst of November 1996 (Roberts and others, 2000;Waller and others, 2001; Björnsson, 2002; Jóhannesson, 2002).

The main conclusions of this study are the following:

1. 1. With a minor adjustment of the governing equations, the Spring–Hutter formulation can be rendered into a system of equations that is straightforward to solve using the numerical method of lines. Recast in this manner, it provides a powerful tool for detailed examination of the hydraulics and thermodynamics of outburst floods.

2. 2. A recalibration of the Manning roughness for outburst floods using the Spring–Hutter model indicates that previous estimates of flow resistance are unreasonably high. The cause of this discrepancy can be traced to the Nye (1976) postulate that dT _w/dt = 0 along the drainage conduit. All previous work using bottleneck models is based on this assumption and thus seriously flawed. The new estimates of channel roughness, though provisional, are consistent with the Manning roughness of natural streams and rivers. Additional work remains to be done in improving the calibration of these models, but better observational data are required before substantial progress can be made.

3. 3. Careful observations of outlet temperature, preferably as a function of time, are lacking, but the Spring–Hutter model, together with earlier work, appears to overestimate the temperature of water exiting the subglacial drainage conduit. It is possible that empirical formulas for heat exchange at the conduit walls are incorrect or inappropriate, but the importance of mechanical abrasion as a process for enlarging ice-walled conduits needs investigation. Even a small amount of abrasion could have a substantial influence on water temperature.

4. 4. The Spring–Hutter model predicts that superflotation water pressures can develop in the drainage conduit, in qualitative agreement with field observations. Excess pressure is greatest at early stages of the outburst and decreases as the flood progresses.

5. 5. The fluid potential gradient along the conduit is not well represented by its value averaged over the length of the conduit.

6. 6. Bottleneck models are unable to capture many important features of outburst flooding, and the basic assumption of bottleneck models, that a spatially fixed flow-controlling seal exists close to the water reservoir, is not generally satisfied. Flow constrictions appear to be highly mobile during the course of an outburst flood, and for some floods the dominant flow constriction is located near the tunnel outlet for much of the flood duration.

What is the prospect for using simulation models to predict glacier flood hazards? It is doubtful that the simple bottleneck models can be reinstated, but this is not necessarily a discouraging outcome. The main justification for bottleneck models was that they were simple to implement, whereas Spring–Hutter models, primarily because of computational challenges, were not. This is no longer the case. Furthermore, Spring–Hutter models have a superior physical basis and, although they seem to require more detailed information about the glacier surface and bed topography, they can perform adequately when such information is sketchy.