Deformational structures at the surge-type glacier Kongsvegen, Svalbard, are displayed at the glacier surface and on a grounded cliff section at the terminus. A 300 m × 65 m grid of 200 MHz ground-penetrating radar (GPR) profiles has been collected adjacent to the cliff section in order to identify englacial structure.Two sub-horizontal reflectors have been imaged; the upper is interpreted as the glacier bed, and represents a transition between glacier ice and frozen subglacial sediments; while the lower is interpreted as a transition between frozen and unfrozen subglacial sediment. Dipping reflectors, corresponding to sediment-filled features on the cliff and glacier surface, do not cross the glacier bed. A small number of reflectors, interpreted as thrust faults, are visible below the bed reflector. A model is developed for structural development, which suggests that ice built up in a reservoir zone during quiescence. During the surge, ice propagated rapidly from this reservoir, creating a zone of compression which resulted in thrusting. Subsequently an extensional flow regime resulted in extensive fracture of the ice. We suggest dilated sediment was evacuated into these extensional crevasses from the glacier bed, accelerating surge termination.

We examine the validity of two methods for estimating glacier equilibrium-line altitudes (ELAs) from topographic maps. The ELA determined by contour inflection (the kinematic ELA) and the mean elevation of the glacier correlate extremely well with the ELA determined from mass-balance data (observed ELA). However, the range in glacier elevations above sea level is much larger than the variation in ELA, making this correlation unhelpful. The data were normalized and a reasonable correlation (r2 = 0.59) was found between observed and kinematic ELA.The average of the normalized kinematic ELAs was consistently located down-glacier from the observed ELA, consistent with theory. The normalized mean elevation of the glacier exhibited no correlation and suggests that the toe–headwall altitude ratio is not a good approximation for the ELA. Kinematic waves had no effect on the position of the kinematic ELA. Therefore, topographic maps of glacier surfaces can be used to infer the position of the ELA and provide a method for estimating past ELAs from historic topographic maps.

This paper presents a glacier ice-flow model that simulates changes to alpine glaciers of various sizes and their runoff response to climate change in the Yili river basin in the Tien Shan mountains, northwestern China. It is suggested that the sensitivity of glaciers to climatic change is determined by glacier size. The change in glacial runoff does not keep pace with climatic change. As climate warms and glaciers retreat, the glacier runoff tends to increase and then decrease. The runoff peak and its timing depend not only on glacier size but also on the rate of air-temperature rise.

In the empirical study of jökulhlaups, the peak discharge, Qmax, and water volume drained by the ice-dammed lake during the floods, Vt, appear to follow a power-law relation 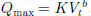, where K are b are constants determined from field data. First identified by Clague and Mathews (1973), this relation is a useful reference for predicting flood magnitude, but its physical origin remains unclear. Here, we develop the theory that connects it to contemporary models for simulating the flood hydrograph. We explain how the function Qmax = f(Vt) arises from Nye’s (1976) theory of time-dependent water flow in a subglacial channel coupled to a lake, and we describe how discharge–volume data record the (monotonically increasing) form of this function so long as the lake is not emptied in the floods. The Grímsvötn jökulhlaups present an example where, because of partial draining of the lake, agreement between the model-derived f and data is excellent. It is documented that other lake systems drain completely, but we explain how the exponent b ≈ 2/3 observed for them collectively is due primarily to a scaling effect related to their size, modified by other factors such as the flood initiation process.

Observations of surface elevation (s) and horizontal velocity components (u and v) are inverted to infer the topography (b) and lubrication (c) at the bed of an ice stream, based on a linearized perturbation theory of the transmission of flow disturbances through the ice thickness. Synthetic data are used to illustrate non-uniqueness in the inversion, but also demonstrate that effects of b and c can be separated when s, u and v are specified, even with added noise to simulate measurement errors. We have analyzed prominent short-horizontal-scale (∼2 km) features in topography and velocity pattern in a local 64 km by 32 km area of the surface of Ice Stream E,West Antarctica. Our preferred interpretation of bed conditions beneath the most prominent features on the surface identifies a deep trough in the basal topography with low lubrication in the base of the trough.

The surface velocity of a predominantly cold polythermal glacier (John Evans Glacier, Ellesmere Island, Canada) varies significantly on both seasonal and shorter time-scales. Seasonal variations reflect the penetration of supraglacial water to the glacier bed through significant thicknesses of cold ice. Shorter-term events are associated with periods of rapidly increasing water inputs to the subglacial drainage system. Early-season short-term events immediately follow the establishment of a drainage connection between glacier surface and glacier bed, and coincide with the onset of subglacial outflow at the terminus. A mid-season short-term event occurred as surface melting resumed following cold weather, and may have been facilitated by partial closure of subglacial channels during this cold period. There is a close association between the timing and spatial distribution of horizontal and vertical velocity anomalies, the temporal pattern of surface water input to the glacier, and the formation, seasonal evolution and distribution of subglacial drainage pathways. These factors presumably control the occurrence of highwater-pressure events and water storage at the glacier bed. The observed coupling between surface water inputs and glacier velocity may allow predominantly cold polythermal glaciers to respond rapidly to climate-induced changes in surface melting.

Ice-flow velocities were measured at Koryto glacier on Kamchatka Peninsula, Russia, during a 37 day period in the middle of the 2000 melt season. Six survey points from the upper to the lower reaches of the glacier exhibited daily fluctuations in surface horizontal speed with major peaks that appeared at all points.We argue that basal motion is the major cause of flow on Koryto glacier. Downward vertical velocities measured over most of the glacier during the survey period are likely due to shrinking of englacial and subglacial cavities. This result may imply that a large amount of water is deposited in the early summer. Since 1960, Koryto glacier has retreated by 450 m and this retreat has accelerated following a decrease in winter precipitation after the mid 1970s.The glacier has thinned by 10–50 m during the last 40 years.

A laboratory experiment was conducted in which new ice crystals were nucleated from the vapor phase onto large existing ice crystals obtained from Antarctic lake ice. Flat, smooth ice-crystal surfaces were prepared, with c axes oriented either vertically or horizontally. When these were subjected to a supersaturated vapor environment, multiple individual crystals nucleated onto the substrates adopting the same crystallographic orientation as the parent. A dominant grain-growth scenario for kinetic-growth metamorphism in snow, which in some ways is analogous to the oriented morphologies in lake ice, is hypothesized. In the lake-ice-growth scenario, optimally oriented crystals will grow at the expense of those less preferentially positioned.The proposed dominant grain-growth theory for snow is in agreement with the observed decrease in the number of grains and the proximal similarity of crystal habit in kinetic-growth metamorphism in snow. Similarly, kinetic crystal growth on the interior of gas inclusions in Antarctic lake ice will also acquire the crystallographic orientation of the substrate ice. These small-faceted interior crystals significantly influence light scattering and penetration in the lake-ice cover.

A simple approach to glacier dynamics is explored in which there is postulated to be a relationship between area and volume with three parameters: the time for area to respond to changes in volume, a thickness scale, and an area characterizing the condition of the initial state.This approach gives a good fit to the measurements of cumulative balance and area on South Cascade Glacier from 1970–97; the area time-scale is roughly 8 years, the thickness scale about 123 m, and the 1970 area roughly 4% larger than required for adjustment with volume. Combining this relationship with a version of mass continuity expressed in terms of area and volume produces a theory of glacier area and volume response to climate in which another time constant, the volume time-scale, appears. Area and volume both respond like a damped spring and mass system. The damping of the South Cascade response is approximately critical, and the volume time-scale is roughly 48 years, six times the area time-scale. The critically damped spring and mass analogy reproduces the time dependence predicted by the more complicated traditional theory of Nye.

This investigation uses Landsat images from 12 days in 1999 and 2000 to study the spatial and temporal variation in surface albedo of a glacier with a rugged topography: Morteratschgletscher, Switzerland. Our retrieval method considers all processes that substantially influence the relationship between the satellite signal and the surface albedo. The correction for the anisotropy of the reflected radiation field of ice and snow ranges up to 0.10, depending on wavelength band, solar zenith angle and surface type. We analyzed the uncertainties in the retrieval method and mainly expect errors in satellite-derived albedos for areas with large variation in topography and high albedos. The latter is due to application of bidirectional reflectance distribution function (BRDF) parameterizations for the anisotropic correction to albedos outside the parameterizations’ validity. On average, satellite-derived albedos exceed the measured surface albedo by 0.03. The glacier tongue is characterized by bands of low and high albedo, relating to ice with higher and lower concentrations of debris. The ice albedo shows no dependence on altitude, except at 2000–2200 m a.s.l. It increases during summer, which is likely associated with rainfall, as concluded from a comparison between summer rainfall and measured albedos.

During the austral summer field season of the Russian Antarctic Expedition in 1999/2000, wide-angle reflections experiments were performed in the vicinity of the Russian station Vostok. A 60 MHz ice radar system with 12-bit digital recording was used. The measurements were taken along two perpendicular lines directed south–north and east–west with a distance of 200 m between marks. We used a one-layer model (without snow–firn zone influence) for the calculations. We calculate that the average velocity of radio-wave propagation in the ice sheet is168.4 ± 0.5 m μs−1.The same velocity was derived from hyperbolic diffractions from internal discontinuities. The results allow more accurate depth interpretation of radio-echo soundings.

Permeability and meltwater flow have been studied in sea ice in the Siberian and central Arctic during the summers of 1995 and 1996. A bail-test technique has been adapted to allow for measurements of in situ permeability, found to range between 10−11 and 10−8 m2. Permeability varied by about a factor of 2 between 1995 (above-normal melt rates) and 1996 (below-normal melt rates). Release of fluorescent tracers (fluorescein, rhodamine) furthermore allowed the derivation of flow velocities and assessment of the relevant driving forces. Hydraulic gradients in rough ice and wind stress in ponded ice were found to be particularly important, driving meltwater over distances of several meters per day. The mid- to late-summer ice was found to be permeable enough to completely divert meltwater from the surface into the ice interior. It is shown, however, that lower permeabilities of the upper ice layers as well as refreezing of meltwater, particularly during the early melt season, foster the development of surface melt ponds.

Automatic feature tracking on two Landsat images (acquired inJanuary 2000 and December 2001) generates a complete and accurate velocity field of Mertz Glacier, East Antarctica. This velocity field shows two main tributaries to the ice stream. Between the tributaries, a likely obstruction feature in the bedrock results in a slow-down of the flow. A third Landsat image, acquired in 1989 and combined with the 2000 image, permits the determination of the glacier mean velocity during the 1990s. Although some parts of the Mertz Glacier system show evidence of slight speed increase, we conclude that the Mertz flow speed is constant within our uncertainty (35 m a−1). Using this complete velocity field, new estimates of the ice discharge flux, 17.8 km3 a−1 (16.4 Gt a−1), and of the basal melting of the tongue, 11 m a−1 of ice, are given. Our results lead to an apparent imbalance of the drainage basin (ice discharge 3.5 km3 a−1 lower than the accumulation). Considering previous studies in the Mertz Glacier area, we then discuss the uncertainty of this imbalance and the problems with accumulation mapping for this region.

The effective viscosity of ice depends upon many factors, including temperature, deviatoric stress, crystal orientation and impurities. A flow law that includes these factors and is simple to implement is a requirement for numerically efficient ice-flow models. The dominant microscale flow mechanism changes as temperature, deviatoric stress or grain-size changes. For both anisotropic and isotropic constitutive relations, this shift in dominant flow mechanism is expressed as a change in the stress exponent. We study the effects of this shift in stress exponent on ice flow using a two-term flow law for isotropic ice. Our stress–strain-rate relationship does not explicitly describe the microscale processes of ice deformation; however, it encompasses a range of deformation behaviors with a simple law. In terrestrial ice, a flow-mechanism shift may occur in low-deviatoric-stress regions near ice divides, resulting in a near-linear constitutive relationship for ice flow. Compared to a non-linear (Glen) divide, a divide dominated by a near-linear flow mechanism has vertical-velocity profiles that are similar at divide and flank sites, internal layers that do not develop a Raymond bump, and a steady-state surface profile that is more rounded near the divide.

A series of experiments was undertaken to determine the origin of filaments found in grain boundaries and impurity spots found in grain interiors of polar ice during observation in the scanning electron microscope. It is shown that although the filaments are artifacts, they demonstrate the presence of impurities segregated to the grain boundary planes. It is also demonstrated that the impurities observed in the grain interior reside there and were not transported from the grain boundaries during specimen preparation or observation.

Two disintegration events leading to the loss of Larsen A and B ice shelves, Antarctic Peninsula, in 1995 and 2002, respectively, proceeded with extreme rapidity (order of several days) and reduced an extensive, seemingly integrated ice shelf to ajumble of small fragments. These events strongly correlate with warming regional climate and accumulation of surface meltwater, supporting a hypothesis that meltwater-induced propagation of pre-existing surface crevasses may have initiated ice-shelf fragmentation.We address here an additional, subsequent mechanism that may sustain and accelerate the ice-shelf break-up once it begins. The proposed mechanism involves the coherent capsize of narrow (less than thickness) ice-shelf fragments by rolling 90° in a direction toward, or away from, the ice front. Fragment capsize liberates gravitational potential energy, forces open ice-shelf rifts and contributes to further fragmentation of the surrounding ice shelf.

A series of laboratory experiments in a 6 m long chute using glass particles of mean diameter 100 μm were performed to investigate the interaction of a supercritical, granular flow with obstacles. It was found that the collision of the flow with a row of mounds led to the formation of a jet, whereby a large fraction of the flow was launched from the top of the mounds and subsequently landed back on the chute. The retarding effect of the mounds was investigated quantitatively by direct measurements of the velocity of the flow, its runout length and the geometry of the jet. The effects of several aspects of the layout of the mounds on their retarding effects were examined. It was observed that a row of steep mounds with an elongated shape in the transverse direction to the flow and with a height several times the flow depth led to dissipation of a large proportion of the kinetic energy of the flow.

Shallow lakes cover >25% of Alaska’s Arctic Coastal Plain. These remain frozen and snow-covered from October to June. The lake snow is thinner, denser, harder and has less water equivalent than snow on the surrounding tundra. Itcontains less depth hoar than land snow, yet paradoxically is subject to stronger temperature gradients. It also has fewer layers and these have been more strongly affected by wind. Dunes and drifts are better developedon lakes; they have wavelengths of 5–20 m, compared to <5 m on land. Because of these differences, lake snow has roughly half the thermal insulating capacity of land snow. The winter mass balance on lakes is also different because (1) some snow falls into the water before the lakes freeze, (2) some snow accumulates in drifts surrounding the lakes, and (3) prevailing winds lead to increased erosion and thinner snow on the eastern lake sides. Physical models that extrapolate land snow over lakes without appropriate adjustments for depth, density, distribution and thermal properties will under-predict ice thickness and winter heat losses.

A statistical analysis of the lengths of grain-boundary and transgranular cracks induced during the initial straining of columnar-grain ice by a compressive load applied perpendicular to the long direction of the columns is presented. The analysis shows that the crack lengths are randomly distributed and form distinct but correlated populations.The lognormal distribution function is shown to be a good descriptor of the populations for 5–90% of their range. Statistical models are presented for the lognormal behaviour of the crack-length distribution and for the strain dependence of the crack density. The models assume that a change in the value of the random variable of the respective population depends on the population value of the variable at the time of the change. It is shown that the model for the strain dependence of the crack density is suitable for the strain dependence of the acoustic emission, measured in both columnar-grain and granular ice subject to constant compressive loads. Evidence is also presented for a lognormal dependence of the dislocation density on strain. The analysis demonstrates that the cracks that form during the initial straining of polycrystalline ice are independent, random events and that the resulting crack populations are precursors to failure by fracture.

Measurements of changes in surface height carried out with sonic altimeters mounted on automatic weather stations in Dronning Maud Land (DML) and on Berkner Island, Antarctica, are used to derive the surface mass balance. The surface mass balance is positive at all sites, i.e. accumulation outweighs ablation. The spatial and temporal variability in accumulation is high. Accumulation occurs in numerous small events and a few large events per year. The larger events contribute more to the annual accumulation than the small events; ∼50% of all accumulation is contributed by 10–25% of all events. The accumulation generally decreases with increasing distance from the coast and elevation. Annual averaged values range from ∼375 ± 59 mm w.e. a−1 near the coast to ∼33 ± 25 mm w.e. a−1 on theAntarctic plateau and are in good agreement with long-term averaged annual accumulation rates obtained from snow pits and firn cores. The records show seasonal dependency of the amount of accumulation, with a maximum in winter in the coastal and escarpment region of DML and in summer on Berkner Island and on the plateau. The seasonal cycles are significant on Berkner Island, and in the coastal area and part of the escarpment region.