The performance of a thermal ice-drill having a smooth, solid, impervious frontal surface, termed a “solid-nose hotpoint”, is determined by the velocities, pressures, and temperatures in the thin layer of warm melt water between the hotpoint and the ice. The efficiency, the speed of penetration, the temperature of the frontal surface, and the distribution of pressure on it can be calculated from the equations of non-turbulent fluid flow. For hotpoints whose frontal surfaces are isothermal and axially symmetric, these quantities are functions of the total input of power Q of the weight W on the hotpoint, of the radius a and “shape factor” S of the frontal surface, and of the pertinent physical properties of water and ice. The calculation shows that with increasing “performance number” 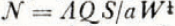 the efficiency E decreases and the surface temperature θ0 increases. Thus, for example, E = 1·00 and θ0 = 0°C. when N = 0.0 E = 0·76 and θ0 = 48°C when N = 1.4; and E = 0·60 and θ0 = 103°C. when N = 3.0. The coefficient Λ is a constant equal to
the efficiency E decreases and the surface temperature θ0 increases. Thus, for example, E = 1·00 and θ0 = 0°C. when N = 0.0 E = 0·76 and θ0 = 48°C when N = 1.4; and E = 0·60 and θ0 = 103°C. when N = 3.0. The coefficient Λ is a constant equal to 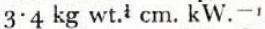 . The shape factor S is a dimensionless number between 0 and 1 that varies according to the shape of the frontal surface, greater values of S being associated with blunter profiles (thus S = 1.0 for a plane frontal surface perpendicular to the axis). For coring hotpoints the same numerical results are obtained, but the performance number is given by
. The shape factor S is a dimensionless number between 0 and 1 that varies according to the shape of the frontal surface, greater values of S being associated with blunter profiles (thus S = 1.0 for a plane frontal surface perpendicular to the axis). For coring hotpoints the same numerical results are obtained, but the performance number is given by
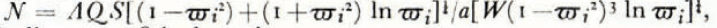
where 2ϖia is the inside diameter of the hotpoint.