Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barańczuk, Stefan
2017.
On a dynamical local–global principle in Mordell–Weil type groups.
Expositiones Mathematicae,
Vol. 35,
Issue. 2,
p.
206.

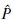 ) ∈
) ∈ 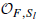 then
then 