Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Biswas, Indranil
Dhillon, Ajneet
and
Lemire, Nicole
2012.
The Essential Dimension of Stacks of Parabolic Vector Bundles over Curves.
Journal of K-theory,
Vol. 10,
Issue. 3,
p.
455.
Basu, Suratno
Biswas, Indranil
and
Dan, Krishanu
2018.
Stability of the parabolic Poincaré bundle.
International Journal of Geometric Methods in Modern Physics,
Vol. 15,
Issue. 05,
p.
1850081.
Bhosle, Usha N.
and
Biswas, Indranil
2023.
Brauer and Picard groups of moduli spaces of parabolic vector bundles on a real curve.
Communications in Algebra,
Vol. 51,
Issue. 9,
p.
3952.
Biswas, Indranil
Chakraborty, Sujoy
and
Dey, Arijit
2024.
Brauer group of moduli stack of stable parabolic PGL(r)-bundles over a curve.
International Journal of Mathematics,
Vol. 35,
Issue. 01,
Bhosle, Usha N.
2024.
Brauer groups and Picard groups of the moduli of parabolic vector bundles on a nodal curve.
Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry,
Vol. 65,
Issue. 3,
p.
751.

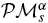 be a moduli space of stable parabolic vector bundles of rank
be a moduli space of stable parabolic vector bundles of rank 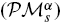 is isomorphic to the cyclic group ℤ/
is isomorphic to the cyclic group ℤ/