Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T12:20:20.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomological obstruction theory for Brauer classes and the period-index problem

Published online by Cambridge University Press:  13 December 2010

Benjamin Antieau
Benjamin Antieau
Affiliation:
UCLA, Math Department, 520 Portola Plaza, Los Angeles, CA 90095-1555, antieau@math.ucla.edu
Get access

Abstract

Let U be a connected noetherian scheme of finite étale cohomological dimension in which every finite set of points is contained in an affine open subscheme. Suppose that α is a class in H2(Uét,ℂm)tors. For each positive integer m, the K-theory of α-twisted sheaves is used to identify obstructions to α being representable by an Azumaya algebra of rank m2. The étale index of α, denoted eti(α), is the least positive integer such that all the obstructions vanish. Let per(α) be the order of α in H2(Uét,ℂm)tors. Methods from stable homotopy theory give an upper bound on the étale index that depends on the period of α and the étale cohomological dimension of U; this bound is expressed in terms of the exponents of the stable homotopy groups of spheres and the exponents of the stable homotopy groups of B(ℤ/(per(α))). As a corollary, if U is the spectrum of a field of finite cohomological dimension d, then 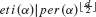, where [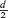] is the integer part of 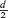, whenever per(α) is divided neither by the characteristic of k nor by any primes that are small relative to d.

Keywords

Brauer groupstwisted sheaveshigher algebraic K-theorystablehomotopy theory
Type
Research Article
Information
Journal of K-Theory , Volume 8 , Issue 3 , December 2011 , pp. 419 - 435
Copyright
Copyright © ISOPP 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Antieau, Benjamin, Čech approximation to the Brown-Gersten spectral sequence, submitted, http://arxiv.org/abs/0909.3786, 2010.Google Scholar
2.Artin, M., On the joins of Hensel rings, Advances in Math. 7, (1971), 282–296 (1971). MR0289501CrossRefGoogle Scholar
3.Artin, M., Brauer-Severi varieties, Brauer groups in ring theory and algebraic geometry (Wilrijk, 1981), Lecture Notes in Math. 917, Springer, Berlin, 1982, 194–210. MR657430Google Scholar
4.Artin, M., Grothendieck, A., and Verdier, J. L. (eds.), Théorie des topos et cohomologie étale des schémas. Tome 2, Lecture Notes in Mathematics 270, Springer-Verlag, Berlin, 1972, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Dirigé par M. Artin, A. Grothendieck et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat. MR0354653Google Scholar
5.Becher, Karim Johannes and Hoffmann, Detlev W., Symbol lengths in Milnor K-theory, Homology Homotopy Appl. 6, (2004) (1), 17–31 (electronic). MR2061565Google Scholar
6.Bousfield, A. K. and Friedlander, E. M., Homotopy theory of Γ-spaces, spectra, and bisimplicial sets, Geometric applications of homotopy theory (Proc. Conf., Evanston, Ill., 1977), II, Lecture Notes in Math. 658, Springer, Berlin, 1978, 80–130. MR513569Google Scholar
7.Colliot-Thélène, J.-L., Gille, P., and Parimala, R., Arithmetic of linear algebraic groups over 2-dimensional geometric fields, Duke Math. J. 121 (2004) (2), 285–341. MR2034644Google Scholar
8.Colliot-Thélène, J.-L., Ojanguren, M., and Parimala, R., Quadratic forms over fraction fields of two-dimensional Henselian rings and Brauer groups of related schemes, Algebra, arithmetic and geometry, Part I, II (Mumbai, 2000), Tata Inst. Fund. Res. Stud. Math. 16, Tata Inst. Fund. Res., Bombay, 2002, 185–217. MR1940669Google Scholar
9.Căldăraru, Andrei, Derived categories of twisted sheaves on Calabi-Yau manifolds, Ph.D. thesis, Cornell University, May 2000, http://www.math.wisc.edu/~andreic/.Google Scholar
10.de Jong, A.J., The period-index problem for the Brauer group of an algebraic surface, Duke Math. J. 123 (2004) (1), 71–94. MR2060023CrossRefGoogle Scholar
11.Edidin, Dan, Hassett, Brendan, Kresch, Andrew, and Vistoli, Angelo, Brauer groups and quotient stacks, Amer. J. Math. 123 (2001) (4), 761–777. MR1844577CrossRefGoogle Scholar
12.Fantechi, Barbara, Göttsche, Lothar, Illusie, Luc, Kleiman, Steven L., Nitsure, Nitin, and Vistoli, Angelo, Fundamental algebraic geometry, Mathematical Surveys and Monographs 123, American Mathematical Society, Providence, RI, 2005, Grothendieck's FGA explained. MR2222646Google Scholar
13.Grayson, Daniel, Higher algebraic K-theory. II (after Daniel Quillen), Algebraic K-theory (Proc. Conf., Northwestern Univ., Evanston, Ill., 1976), Springer, Berlin, 1976, 217–240. Lecture Notes in Math. 551. MR0574096Google Scholar
14.Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Inst. Hautes Études Sci. Publ. Math. (1966) (28), 255. MR0217086Google Scholar
15.Holzsager, Richard, Stable splitting of K(G,1), Proc. Amer. Math. Soc. 31 (1972), 305–306. MR0287540Google Scholar
16.Lieblich, Max, Period and index in the brauer group of an arithmetic surface (with an appendix by Daniel Krashen), 2007, http://arxiv.org/abs/math/0702240.Google Scholar
17.Lieblich, Max, Twisted sheaves and the period-index problem, Compos. Math. 144 (2008) (1), 1–31. MR2388554CrossRefGoogle Scholar
18.Lieblich, Max, The period-index problem for fields of transcendence degree 2, 2009, http://arxiv.org/abs/0909.4345.Google Scholar
19.Merkurjev, A. S., Kaplansky's conjecture in the theory of quadratic forms, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 175 (1989), no. Koltsa i Moduli. 3, 75–89, 163-164. MR1047239Google Scholar
20.Ravenel, Douglas C., Complex cobordism and stable homotopy groups of spheres, Pure and Applied Mathematics 121, Academic Press Inc., Orlando, FL, 1986. MR860042Google Scholar
21.Saltman, David J., Division algebras over p-adic curves, J. Ramanujan Math. Soc. (1997) (1), 25–47. MR1462850Google Scholar
22.Suslin, Andrei A., On the K-theory of local fields, J. Pure Appl. Algebra 34 (1984) (2-3), 301–318. MR772065CrossRefGoogle Scholar
23.Thomason, R.W., Symmetric monoidal categories model all connective spectra, Theory Appl. Categ. 1 (1995) (5), 78–118 (electronic). MR1337494Google Scholar
24.Thomason, R. W. and Trobaugh, Thomas, Higher algebraic K-theory of schemes and of derived categories, The Grothendieck Festschrift, Vol. III, Progr. Math., vol. 88, Birkhäuser Boston, Boston, MA, 1990, 247–435. MR1106918Google Scholar
25.Thomason, Robert W., First quadrant spectral sequences in algebraic K-theory via homotopy colimits, Comm. Algebra 10 (1982) (15), 1589–1668. MR668580CrossRefGoogle Scholar
26.Thomason, Robert W., Algebraic K-theory and étale cohomology, Ann. Sci. École Norm. Sup. (4) 18 (1985) (3), 437–552. MR826102CrossRefGoogle Scholar