Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-13T05:59:11.773Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomology for Generalized Bredon Coefficient Systems and Higher K-Theory

Published online by Cambridge University Press:  19 April 2012

Aderemi Kuku
Get access

Abstract

Let 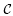be a generalized based category (see definition 1.2). In this paper, we construct a cohomology theory in the category 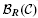of contravariant functors: 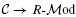where R is a commutative ring with identity, which generalizes Bredon cohomology involving finite, profinite or discrete groups.

We also study higher K-theory of the category 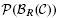of finitely generated projective objects in 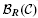and the category 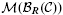of finitely generated objects in 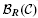and obtain some finiteness and other results.

Keywords

generalized Bredon coefficient systemscohomologygeneralized based categorieshigher K-theoryfiniteprofinite and discrete groups
Type
Research Article
Information
Journal of K-Theory , Volume 12 , Issue 1: Nanjing Special Issue on K-theory, number theory and geometry , August 2013 , pp. 99 - 113
Copyright
Copyright © ISOPP 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Allday, G. and Puppe, V., Cohomological Methods in Transformation Groups, Cambridge Univ. Press, 1973.Google Scholar
2.Bredon, G.E., Introduction to Compact Transformation Groups, Pure and Applied Math. 46, Academic Press, New York, 1972.Google Scholar
3.Hilton, P.J. and Stammbach, U., A Course in Homological Algebra, Springer Verlag, 1971.Google Scholar
4.Kuku, A.O., K-theory of Group-rings of Finite Groups over Maximal Orders in Division Algebras, J. Algebra 91(1) (1984), 18–31.Google Scholar
5.Kuku, A.O., Kn, SKn of Integral Group-rings and Orders, Contemp. Math. 55 (1986), 333–338.Google Scholar
6.Kuku, A.O., Higher K-theory of Modules over EI-categories, Afrika Mat 3 (1996), 15–27.Google Scholar
7.Kuku, A.O., Ranks of Kn and Gn of Orders and Group-rings of Finite Groups over Integers in Number Fields, J. Pure & Appl. Alg. 138 (1999), 39–44.Google Scholar
8.Kuku, A.O., Profinite and Continuous Higher K-theory of Exact Categories Orders and grouprings, K-Theory 22 (2001), 367–392.Google Scholar
9.Kuku, A.O., Finiteness of Higher K-groups of Orders and Group-rings, K-Theory 36 (2005), 51–58.Google Scholar
10.Kuku, A.O., Representation Theory and Higher Algebraic K-theory, Chapman and Hall, 2007.Google Scholar
11.Luck, W., Transformation Groups and Algebraic K-theory, Lecture Notes in Math, Springer-Verlag, Berlin, 1971.Google Scholar
12.MacLane, S., Categories for the Working Mathematician, Springer-Verlag, Berlin, 1971.Google Scholar
13.Mislin, G. and Valette, A., Proper Group Actions and the Baum-Connes Conjecture, Advanced Courses in Mathematics, CRM, Barcelona, Birkhäuser, 2003.Google Scholar
14.Quillen, D., Higher Algebraic K-theory I, Springer-Verlag, SLN 341, 1973.Google Scholar