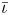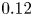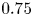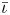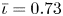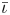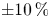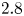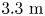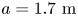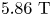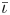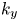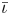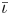1. Introduction
Stellarators are toroidal magnetic confinement devices that rely on non-axisymmetric magnetic fields to confine a plasma. Non-axisymmetry makes it possible to produce the confining magnetic field using currents external to the plasma. However, without an explicit symmetry direction, particles are not guaranteed to be confined by conservation laws, and the magnetic field must be optimized to confine particles.
One possible optimization strategy is to optimize for a property known as quasi-symmetry (Boozer Reference Boozer1983), in which the magnitude of the magnetic field has a symmetry in a special set of coordinates. Over the last few years, tremendous progress has been made in optimizing stellarator geometries to achieve excellent quasi-symmetry (Landreman & Paul Reference Landreman and Paul2022). However, the results so far are mostly limited to configurations scattered in parameter space, which makes it hard to systematically study the effects of varying equilibrium parameters, such as the rotational transform $\iota$![]() and global magnetic shear $\hat {s}$
and global magnetic shear $\hat {s}$![]() .
.
In this paper, we attempt to alleviate this issue by applying continuation methods to continuously deform the rotational transform profile of the ‘Precise QA’ vacuum configuration described in Landreman & Paul (Reference Landreman and Paul2022). This procedure lets us generate a family of stellarator geometries that are similar to each other in a sense that is explained in the next section, but where the rotational transform profile varies.
Since the mean rotational transform of the original ‘Precise QA’ configuration was arbitrarily imposed, it is not a priori obvious that there are any inherent trade-offs between quasi-symmetry and different values of mean $\iota$![]() . Increasing the rotational transform is expected to improve the fast-particle confinement, since the width of banana orbits scales $\propto 1 / \iota$
. Increasing the rotational transform is expected to improve the fast-particle confinement, since the width of banana orbits scales $\propto 1 / \iota$![]() (Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022), and could thus be beneficial for a reactor.
(Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022), and could thus be beneficial for a reactor.
Optimization by continuation is a technique whereby an optimization problem is solved by continuously deforming a simpler optimization problem. If each deformation is a small perturbation to the previous problem, the solution of the previous problem can be used as a good initial guess to the perturbed problem. By repeatedly applying small perturbations and optimizing at each step, we eventually arrive at a solution to the novel optimization problem.
A variety of continuation-type methods have been used for stellarator equilibrium and optimization calculations previously. The code Desc allows for magnetohydrodynamic equilibria to be computed by continuation in the plasma boundary shape or plasma profiles (Conlin et al. Reference Conlin, Dudt, Panici and Kolemen2023). One common optimization approach – optimizing first in a small parameter space of Fourier modes describing the plasma shape, then expanding the number of Fourier modes in the parameter space and re-optimizing – can be viewed as a type of continuation method. This approach was discussed for instance in Landreman & Paul (Reference Landreman and Paul2022). Continuation is also a standard method for exploring the Pareto front in multi-objective optimization, and has recently seen use in this context to explore the trade-offs between quasi-symmetry and aspect ratio (Bindel, Landreman & Padidar Reference Bindel, Landreman and Padidar2023).
Larger systematic explorations of the space of quasi-symmetric stellarators have previously been published by Landreman (Reference Landreman2022), which relied on the near-axis expansion to directly construct optimized stellarator equilibria (Landreman, Sengupta & Plunk Reference Landreman, Sengupta and Plunk2019; Plunk, Landreman & Helander Reference Plunk, Landreman and Helander2019). In contrast, our geometries are solutions to the full equilibrium equation, with a realistic number of Fourier modes describing the boundary. Giuliani et al. (Reference Giuliani, Wechsung, Cerfon, Landreman and Stadler2023) recently made public a large database of quasi-axisymmetric (QA) stellarators with varying $\bar {\iota }$![]() , which could be used to perform studies similar to this one.
, which could be used to perform studies similar to this one.
While there is a rich mathematical literature on continuation methods (also known as homotopy methods), see for example Allgower & Georg (Reference Allgower and Georg2003), the application of the method to practical optimization problems is often based more on intuition than on mathematical rigour (Mobahi & Fisher Reference Mobahi and Fisher2015). This is also the approach taken here.
The rest of the paper is organized as follows. In the next section, we present the objective function used in the optimization, and introduce the continuation method. In § 3, we apply this method to generate ‘Precise QA’-like configurations with varying mean rotational transform or shear. We analyse these configurations with respect to fast-particle confinement, gyrokinetic stability and required coil–plasma distance. We find that fast-particle confinement improves with higher $\bar {\iota }$![]() , up to a point, while the maximum growth rate in our gyrokinetic simulations increases and shifts towards higher $k_y$
, up to a point, while the maximum growth rate in our gyrokinetic simulations increases and shifts towards higher $k_y$![]() . Finally, we discuss the results in § 4. All the equilibria presented here can be found as supplemental material on Zenodo at https://zenodo.org/doi/10.5281/zenodo.10521393 (see Buller Reference Buller2024).
. Finally, we discuss the results in § 4. All the equilibria presented here can be found as supplemental material on Zenodo at https://zenodo.org/doi/10.5281/zenodo.10521393 (see Buller Reference Buller2024).
2. Theory
A magnetic field $\boldsymbol {B}$![]() is quasi-symmetric with helicity $(M,N)$
is quasi-symmetric with helicity $(M,N)$![]() if its magnitude $B = |\boldsymbol {B}|$
if its magnitude $B = |\boldsymbol {B}|$![]() can be written as
can be written as
where $\psi$![]() is a flux-surface label, which we take to be the toroidal flux divided by $2{\rm \pi}$
is a flux-surface label, which we take to be the toroidal flux divided by $2{\rm \pi}$![]() , and $\vartheta$
, and $\vartheta$![]() and $\zeta$
and $\zeta$![]() are magnetic angles, which we take to be the Boozer angles. Compared with the generic case where $B = B(\psi,\vartheta,\zeta )$
are magnetic angles, which we take to be the Boozer angles. Compared with the generic case where $B = B(\psi,\vartheta,\zeta )$![]() depends on all angles independently, the Lagrangian of a charged particle travelling through a quasi-symmetric field has a symmetry direction when written in Boozer coordinates, which ensures that the charged particle is confined by the magnetic field (Boozer Reference Boozer1983; Nührenberg & Zille Reference Nührenberg and Zille1988; Rodriguez, Helander & Bhattacharjee Reference Rodriguez, Helander and Bhattacharjee2020). The symmetry direction depends on $M$
depends on all angles independently, the Lagrangian of a charged particle travelling through a quasi-symmetric field has a symmetry direction when written in Boozer coordinates, which ensures that the charged particle is confined by the magnetic field (Boozer Reference Boozer1983; Nührenberg & Zille Reference Nührenberg and Zille1988; Rodriguez, Helander & Bhattacharjee Reference Rodriguez, Helander and Bhattacharjee2020). The symmetry direction depends on $M$![]() and $N$
and $N$![]() : fields with $N=0$
: fields with $N=0$![]() are known as QA; fields with non-zero $N$
are known as QA; fields with non-zero $N$![]() and $M$
and $M$![]() are called quasi-helically symmetric.
are called quasi-helically symmetric.
As the Boozer angles $\vartheta$![]() and $\zeta$
and $\zeta$![]() themselves depend on $\boldsymbol {B}$
themselves depend on $\boldsymbol {B}$![]() , it is not known how to directly compute fields with quasi-symmetry, except for the case where the fields possess exact axisymmetry ($\boldsymbol {B} = \boldsymbol {B}(\psi,\vartheta )$
, it is not known how to directly compute fields with quasi-symmetry, except for the case where the fields possess exact axisymmetry ($\boldsymbol {B} = \boldsymbol {B}(\psi,\vartheta )$![]() ). Using different asymptotic methods for finding quasi-symmetry typically yields overdetermined systems of equations beyond a certain order (Garren & Boozer Reference Garren and Boozer1991; Plunk & Helander Reference Plunk and Helander2018), which suggests that exact quasi-symmetry apart from true axisymmetry may be impossible to achieve. The approach taken historically is to instead optimize $\boldsymbol {B}$
). Using different asymptotic methods for finding quasi-symmetry typically yields overdetermined systems of equations beyond a certain order (Garren & Boozer Reference Garren and Boozer1991; Plunk & Helander Reference Plunk and Helander2018), which suggests that exact quasi-symmetry apart from true axisymmetry may be impossible to achieve. The approach taken historically is to instead optimize $\boldsymbol {B}$![]() to achieve approximate quasi-symmetry, which can yield configurations that are good enough in practice. This is also the approach taken in this paper.
to achieve approximate quasi-symmetry, which can yield configurations that are good enough in practice. This is also the approach taken in this paper.
As in Landreman & Paul (Reference Landreman and Paul2022), we take our objective function to be
where $A$![]() is the aspect ratio, $\bar {\iota }$
is the aspect ratio, $\bar {\iota }$![]() is the mean (over $\psi$
is the mean (over $\psi$![]() ) of the rotational transform and $f_{\text {QS}}$
) of the rotational transform and $f_{\text {QS}}$![]() is the so-called two-term formulation of quasi-symmetry (Helander & Simakov Reference Helander and Simakov2008). Specifically
is the so-called two-term formulation of quasi-symmetry (Helander & Simakov Reference Helander and Simakov2008). Specifically

where the sum is over flux surfaces, $\langle \boldsymbol {\cdot } \rangle$![]() denotes the flux-surface average and $2{\rm \pi} G/\mu _0$
denotes the flux-surface average and $2{\rm \pi} G/\mu _0$![]() and $2{\rm \pi} I/\mu _0$
and $2{\rm \pi} I/\mu _0$![]() are the poloidal current outside and toroidal current inside the flux surface, respectively. The $f_{\text {QS}}$
are the poloidal current outside and toroidal current inside the flux surface, respectively. The $f_{\text {QS}}$![]() objective is zero when $\boldsymbol {B}$
objective is zero when $\boldsymbol {B}$![]() is quasi-symmetric with helicity $(M,N)$
is quasi-symmetric with helicity $(M,N)$![]() , so different kinds of quasi-symmetry can be targeted by specifying $M$
, so different kinds of quasi-symmetry can be targeted by specifying $M$![]() and $N$
and $N$![]() . The second and third terms on the right-hand side of (2.2) target a specific aspect ratio $A_*$
. The second and third terms on the right-hand side of (2.2) target a specific aspect ratio $A_*$![]() and mean rotational transform $\bar {\iota }_*$
and mean rotational transform $\bar {\iota }_*$![]() , respectively.
, respectively.
The above objective is optimized with respect to the boundary shape of the plasma, which is described in terms of Fourier modes. The boundary can be described by

where $R$![]() , $Z$
, $Z$![]() , $\phi$
, $\phi$![]() are the cylindrical coordinates of our surface, $M_{\textrm {pol}}$
are the cylindrical coordinates of our surface, $M_{\textrm {pol}}$![]() and $N_{\textrm {tor}}$
and $N_{\textrm {tor}}$![]() are the maximum poloidal and toroidal mode numbers in our representation and $n_{\textrm {fp}}$
are the maximum poloidal and toroidal mode numbers in our representation and $n_{\textrm {fp}}$![]() is the number of field-periods of the geometry. Throughout this work, stellarator symmetry is assumed, which eliminates the sine and cosine components in $R$
is the number of field-periods of the geometry. Throughout this work, stellarator symmetry is assumed, which eliminates the sine and cosine components in $R$![]() and $Z$
and $Z$![]() , respectively. The poloidal angle $\theta$
, respectively. The poloidal angle $\theta$![]() is arbitrary. Typically, $M_{\textrm {pol}} = N_{\textrm {tor}}=6$
is arbitrary. Typically, $M_{\textrm {pol}} = N_{\textrm {tor}}=6$![]() in our optimizations.
in our optimizations.
For each boundary, a magnetic equilibrium is calculated using the Vmec code (Hirshman & Whitson Reference Hirshman and Whitson1983) and the objective is evaluated for this calculated equilibrium. The optimization is formulated using the Simsopt framework (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021). We use the Trust Region Reflective method in scipy to find a local minimum given an initial condition (Virtanen et al. Reference Virtanen2020).
2.1. Computational procedure
We generate our equilibria by solving a series of local optimization problems with different $\bar {\iota }_*$![]() , using a continuation method.
, using a continuation method.
Let $F[\bar {\iota }_*]$![]() denote the objective function (2.2) with a specific value of $\bar {\iota }_*$
denote the objective function (2.2) with a specific value of $\bar {\iota }_*$![]() . Let $F^{(0)} = F[\bar {\iota }_*^{(0)}]$
. Let $F^{(0)} = F[\bar {\iota }_*^{(0)}]$![]() and let $\boldsymbol {x}^{(0)}$
and let $\boldsymbol {x}^{(0)}$![]() be an optimum to this objective. We define our series of optimization problems through
be an optimum to this objective. We define our series of optimization problems through
and take $\boldsymbol {x}^{(n)}$![]() to denote the optimum of $F^{(n)}$
to denote the optimum of $F^{(n)}$![]() .
.
Since we are doing local optimizations, the obtained optimum for a given $F^{(n)}$![]() will depend on the initial guess. For each new optimization problem $F^{(n+1)}$
will depend on the initial guess. For each new optimization problem $F^{(n+1)}$![]() , we use the optimum from the previous optimization problem $F^{(n)}$
, we use the optimum from the previous optimization problem $F^{(n)}$![]() as our initial guess. If $\varDelta \bar {\iota }_*$
as our initial guess. If $\varDelta \bar {\iota }_*$![]() is small, we expect $F^{(n+1)}$
is small, we expect $F^{(n+1)}$![]() to be roughly equal to $F^{(n)}$
to be roughly equal to $F^{(n)}$![]() with a small perturbation, and $\boldsymbol {x}^{(n)}$
with a small perturbation, and $\boldsymbol {x}^{(n)}$![]() can thus be expected to be close to the new optimum $\boldsymbol {x}^{(n+1)}$
can thus be expected to be close to the new optimum $\boldsymbol {x}^{(n+1)}$![]() . If this expectation holds, our procedure will generate a series of equilibria with different $\bar {\iota }_*$
. If this expectation holds, our procedure will generate a series of equilibria with different $\bar {\iota }_*$![]() that are otherwise similar, in the sense of being close to each other in the space of Fourier boundary modes over which we optimize.
that are otherwise similar, in the sense of being close to each other in the space of Fourier boundary modes over which we optimize.
3. Results
In this section, we present measures of quasi-symmetry, fast-particle confinement and ion-temperature-gradient (ITG) stability for the different geometries obtained using the procedure described in § 2.1. Quasi-symmetry is part of the objective function (2.2), and can thus be considered a measure of how well the optimizer performs for the different $\bar {\iota }_*$![]() . The other figures of merit were not explicitly optimized for.
. The other figures of merit were not explicitly optimized for.
3.1. Exploring the optimization landscape around an optimum
Before presenting detailed results of our optimized configurations, it is instructive to look at the optimization landscape around an optimum and how it changes when going to the next $\bar {\iota }_*$![]() . In figure 1, we plot the objective function when varying each of the Fourier boundary modes about our optimum for $\bar {\iota }_* = 0.42$
. In figure 1, we plot the objective function when varying each of the Fourier boundary modes about our optimum for $\bar {\iota }_* = 0.42$![]() . Each panel corresponds to a different boundary mode, indicated above the plot. The $y$
. Each panel corresponds to a different boundary mode, indicated above the plot. The $y$![]() axes and $x$
axes and $x$![]() axes correspond to the value of the objective and the boundary mode, respectively. Colour is used to indicate the range of the $y$
axes correspond to the value of the objective and the boundary mode, respectively. Colour is used to indicate the range of the $y$![]() axis. The range of the $x$
axis. The range of the $x$![]() axis covers a $30\,\%$
axis covers a $30\,\%$![]() relative change in the corresponding boundary parameter.
relative change in the corresponding boundary parameter.

Figure 1. Solid lines: variation in the objective (2.2) for $\bar {\iota }_*=0.42$![]() for a scan in boundary modes around the corresponding optimum. Each panel corresponds to a scan in one boundary mode, as indicated above the panel. Each boundary mode is varied by up to ${\pm }30\,\%$
for a scan in boundary modes around the corresponding optimum. Each panel corresponds to a scan in one boundary mode, as indicated above the panel. Each boundary mode is varied by up to ${\pm }30\,\%$![]() and the colours correspond to the range of values taken by the objective along that curve. Dashed lines: objective evaluated for the same boundaries, but with $\bar {\iota }_*=0.43$
and the colours correspond to the range of values taken by the objective along that curve. Dashed lines: objective evaluated for the same boundaries, but with $\bar {\iota }_*=0.43$![]() .
.
From reading the colourbar, we see that the relative sensitivity of the objective to various boundary modes varies by almost eight orders of magnitude. This is largely due to the differences in the absolute values of the original modes. Since several boundary modes have very shallow or even non-existent local wells, our optimum is effectively in a flat valley and is thus not unique. Small changes in the numerical optimization method or initial condition will result in optima where the non-sensitive boundary modes assume different values, within the narrow range plotted.
This ‘non-uniqueness’ suggests that the slight perturbations of the continuation method may cause unpredictable jumps in the insensitive boundary modes. To illustrate the immediate effect of increasing $\bar {\iota }_*$![]() , figure 1 also shows the landscape around the same $\bar {\iota }_*=0.42$
, figure 1 also shows the landscape around the same $\bar {\iota }_*=0.42$![]() optimum after $\bar {\iota }_*$
optimum after $\bar {\iota }_*$![]() in the objective has been changed to $0.43$
in the objective has been changed to $0.43$![]() , corresponding to the initial state of the optimization of the next step in our $\bar {\iota }_*$
, corresponding to the initial state of the optimization of the next step in our $\bar {\iota }_*$![]() scan. For some of the insensitive modes (for example, $m=3, n=0$
scan. For some of the insensitive modes (for example, $m=3, n=0$![]() ), the objective changes from being relatively flat to having an incline over the plotted range. This will push the optimizer to make relatively large jumps in these boundary modes, potentially to different local minima in these insensitive modes.
), the objective changes from being relatively flat to having an incline over the plotted range. This will push the optimizer to make relatively large jumps in these boundary modes, potentially to different local minima in these insensitive modes.
Thus, the continuation method does not strictly follow a unique minimum as the landscape is deformed by changing $\bar {\iota }_*$![]() . Rather, it samples a class of minima with potentially large relative differences in the insensitive modes. In the next section we use the resulting equilibria to evaluate how various figures of merit vary with $\bar {\iota }$
. Rather, it samples a class of minima with potentially large relative differences in the insensitive modes. In the next section we use the resulting equilibria to evaluate how various figures of merit vary with $\bar {\iota }$![]() .
.
3.2. Varying rotational transform in a QA equilibrium
Using the objective function (2.2) with $A_*=6.0$![]() , $N=1$
, $N=1$![]() and $M=0$
and $M=0$![]() in (2.3), we optimize the boundary of an $n_{\textrm {fp}} = 2$
in (2.3), we optimize the boundary of an $n_{\textrm {fp}} = 2$![]() field-period vacuum configuration starting from a purely toroidal field and targeting $\bar {\iota }_* = 0.12$
field-period vacuum configuration starting from a purely toroidal field and targeting $\bar {\iota }_* = 0.12$![]() . We optimize by successively expanding the number of boundary Fourier modes in six steps, only including Fourier modes up to $|n| \leq j, m \leq j$
. We optimize by successively expanding the number of boundary Fourier modes in six steps, only including Fourier modes up to $|n| \leq j, m \leq j$![]() in the $j$
in the $j$![]() th step. This optimization is repeated for six different relative finite-difference step sizes to calculate the rate of change with respect to the different boundary modes $r_{c,m,n}$
th step. This optimization is repeated for six different relative finite-difference step sizes to calculate the rate of change with respect to the different boundary modes $r_{c,m,n}$![]() and $z_{s,m,n}$
and $z_{s,m,n}$![]() , and the optimum with the lowest quasi-symmetry error is picked. The resulting optimum is taken as our initial configuration in the procedure described in the next paragraph.
, and the optimum with the lowest quasi-symmetry error is picked. The resulting optimum is taken as our initial configuration in the procedure described in the next paragraph.
Incrementing $\bar {\iota }_*$![]() by $0.01$
by $0.01$![]() , we redo the optimization starting from the previous optimum. As this is a small adjustment to the objective function, the previous optimum is expected to be a good initial guess. Thus, we immediately optimize with all Fourier boundary modes. This not only saves time, but is also expected to make the resulting series of optima similar to each other. For convenience, all optimizations are performed with the initially found optimal finite-difference step size.
, we redo the optimization starting from the previous optimum. As this is a small adjustment to the objective function, the previous optimum is expected to be a good initial guess. Thus, we immediately optimize with all Fourier boundary modes. This not only saves time, but is also expected to make the resulting series of optima similar to each other. For convenience, all optimizations are performed with the initially found optimal finite-difference step size.
The quasi-symmetry errors of the resulting configurations at the different $\bar {\iota }_*$![]() are plotted in figure 2, alongside the results of rerunning the optimizations from a purely toroidal field at different $\bar {\iota }_*$
are plotted in figure 2, alongside the results of rerunning the optimizations from a purely toroidal field at different $\bar {\iota }_*$![]() . We see that the continuation method results in lower quasi-symmetry error throughout the entire $\bar {\iota }_*$
. We see that the continuation method results in lower quasi-symmetry error throughout the entire $\bar {\iota }_*$![]() range, achieving quasi-symmetry errors about ten times lower than that for the optimization starting from a purely toroidal field. For $\bar {\iota }_* \in [0.2, 0.65]$
range, achieving quasi-symmetry errors about ten times lower than that for the optimization starting from a purely toroidal field. For $\bar {\iota }_* \in [0.2, 0.65]$![]() , the quasi-symmetry error displays a broad valley, where it varies between $2.4 \times 10^{-8}$
, the quasi-symmetry error displays a broad valley, where it varies between $2.4 \times 10^{-8}$![]() and $9.0 \times 10^{-8}$
and $9.0 \times 10^{-8}$![]() .
.

Figure 2. Quasi-symmetry error (2.3) from configurations with varying $\bar {\iota }$![]() . The blue line corresponds to configurations found by the continuation method described in § 2.1. For comparison, we also include optimizations following the same procedure as in Landreman & Paul (Reference Landreman and Paul2022), but targeting different $\bar {\iota }$
. The blue line corresponds to configurations found by the continuation method described in § 2.1. For comparison, we also include optimizations following the same procedure as in Landreman & Paul (Reference Landreman and Paul2022), but targeting different $\bar {\iota }$![]() (orange). Depicted in green is a continuation scan towards lower $\bar {\iota }$
(orange). Depicted in green is a continuation scan towards lower $\bar {\iota }$![]() , showing that the scan is not reversible, which is expected given the ‘non-uniqueness’ of the configurations as discussed in § 3.1. The ‘Precise QA’ (Landreman & Paul Reference Landreman and Paul2022) corresponds to the $\bar {\iota }=0.42$
, showing that the scan is not reversible, which is expected given the ‘non-uniqueness’ of the configurations as discussed in § 3.1. The ‘Precise QA’ (Landreman & Paul Reference Landreman and Paul2022) corresponds to the $\bar {\iota }=0.42$![]() ‘from purely toroidal’ optimization.
‘from purely toroidal’ optimization.
For $0.12 < \bar {\iota }_* < 0.2$![]() , the continuation method gives decreasing quasi-symmetry error for increasing $\bar {\iota }_*$
, the continuation method gives decreasing quasi-symmetry error for increasing $\bar {\iota }_*$![]() . To test whether this is due to lingering effects of the initial configuration at $\bar {\iota }_* = 0.12$
. To test whether this is due to lingering effects of the initial configuration at $\bar {\iota }_* = 0.12$![]() , we run the continuation method in reverse starting from the $\bar {\iota }_*=0.21$
, we run the continuation method in reverse starting from the $\bar {\iota }_*=0.21$![]() configuration. The result is shown in green in figure 2. Due to the ‘non-uniqueness’ property discussed in § 3.1, we do not expect the process to retrace itself exactly when done in reverse. Indeed, we find that the resulting configurations have somewhat different quasi-symmetry error after only two backwards iterations, compared with the previously obtained configurations with the same $\bar {\iota }_*$
configuration. The result is shown in green in figure 2. Due to the ‘non-uniqueness’ property discussed in § 3.1, we do not expect the process to retrace itself exactly when done in reverse. Indeed, we find that the resulting configurations have somewhat different quasi-symmetry error after only two backwards iterations, compared with the previously obtained configurations with the same $\bar {\iota }_*$![]() . These new configurations are not notably better than the configurations obtained by starting from a purely toroidal field. This indicates that higher quasi-symmetry error for $\bar {\iota }_* < 0.20$
. These new configurations are not notably better than the configurations obtained by starting from a purely toroidal field. This indicates that higher quasi-symmetry error for $\bar {\iota }_* < 0.20$![]() is not merely an effect of the initial conditions in the optimization.
is not merely an effect of the initial conditions in the optimization.
Figure 3 shows examples of boundary shapes obtained in the continuation scan. We see that as $\bar {\iota }_*$![]() increases, the boundary shapes become more elongated. This appears to limit the range of achievable $\bar {\iota }_*$
increases, the boundary shapes become more elongated. This appears to limit the range of achievable $\bar {\iota }_*$![]() in the scan, as VMEC eventually fails to solve for the resulting plasma equilibria around $\bar {\iota }_* = 0.81$
in the scan, as VMEC eventually fails to solve for the resulting plasma equilibria around $\bar {\iota }_* = 0.81$![]() . The quasi-symmetry starts to degrade already at $\bar {\iota }_* \approx 0.65$
. The quasi-symmetry starts to degrade already at $\bar {\iota }_* \approx 0.65$![]() , perhaps because of the optimum shape becoming thin enough that it cannot be accurately represented using only boundary Fourier modes up to $|n| \leq 4, m \leq 4$
, perhaps because of the optimum shape becoming thin enough that it cannot be accurately represented using only boundary Fourier modes up to $|n| \leq 4, m \leq 4$![]() .
.

Figure 3. Rows 1 and 2: plasma boundary shapes for select points in the scan ($\bar {\iota }=0.12$![]() , $\bar {\iota }=0.42$
, $\bar {\iota }=0.42$![]() and $\bar {\iota }=0.71$
and $\bar {\iota }=0.71$![]() ). As $\bar {\iota }$
). As $\bar {\iota }$![]() increases, the boundary becomes more elongated. Row 3: $|\boldsymbol {B}|$
increases, the boundary becomes more elongated. Row 3: $|\boldsymbol {B}|$![]() on the boundary in Boozer coordinates.
on the boundary in Boozer coordinates.
One advantage of higher $\bar {\iota }_*$![]() is that the orbit width of charged particles roughly scales as $1/\iota$
is that the orbit width of charged particles roughly scales as $1/\iota$![]() for QA configurations. Specifically, in the small-orbit-width limit, the orbit width is proportional to (Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022)
for QA configurations. Specifically, in the small-orbit-width limit, the orbit width is proportional to (Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022)
We thus expect fast particles to be better confined in QA configurations with higher $\bar {\iota }_*$![]() , all else being equal.
, all else being equal.
This prediction is borne out by particle tracing simulations using the collisionless guiding-centre orbit solver Simple (Albert, Kasilov & Kernbichler Reference Albert, Kasilov and Kernbichler2020a,Reference Albert, Kasilov and Kernbichlerb). Figure 4 shows the loss fractions calculated by tracing $5000$![]() alpha particles with $3.52\ \mathrm {MeV}$
alpha particles with $3.52\ \mathrm {MeV}$![]() energy for $0.2$
energy for $0.2$![]() s. The particles were launched at three different radii, and considered lost when crossing the last closed flux surface at normalized toroidal flux $s=1.0$
s. The particles were launched at three different radii, and considered lost when crossing the last closed flux surface at normalized toroidal flux $s=1.0$![]() . The configurations have all been scaled up to a reactor-relevant minor radius of $1.704 \mathrm {m}$
. The configurations have all been scaled up to a reactor-relevant minor radius of $1.704 \mathrm {m}$![]() and volume-average magnetic field of $5.865\ \mathrm {T}$
and volume-average magnetic field of $5.865\ \mathrm {T}$![]() , to match the ARIES-CS configuration (Najmabadi et al. Reference Najmabadi2008). We see that the confinement improves with $\bar {\iota }$
, to match the ARIES-CS configuration (Najmabadi et al. Reference Najmabadi2008). We see that the confinement improves with $\bar {\iota }$![]() until about $\bar {\iota } = 0.73$
until about $\bar {\iota } = 0.73$![]() , where the increase in quasi-symmetry error outweighs the benefits of increasing $\bar {\iota }$
, where the increase in quasi-symmetry error outweighs the benefits of increasing $\bar {\iota }$![]() .
.

Figure 4. Fast-particle loss fraction for the different $\bar {\iota }$![]() configurations as calculated by Simple by tracing $5000$
configurations as calculated by Simple by tracing $5000$![]() alpha particles released at the surfaces with normalized toroidal flux $s=0.3$
alpha particles released at the surfaces with normalized toroidal flux $s=0.3$![]() , $s=0.5$
, $s=0.5$![]() , $s=0.7$
, $s=0.7$![]() . The dashed lines show least-squares fits of $c\,\bar {\iota }_*^{\alpha }$
. The dashed lines show least-squares fits of $c\,\bar {\iota }_*^{\alpha }$![]() to the data, with fit parameters $c$
to the data, with fit parameters $c$![]() and $\alpha$
and $\alpha$![]() shown in the figure.
shown in the figure.
To see to which extent the $1/\iota$![]() orbit-width scaling is reflected in the fast-particle losses, we fit the losses to $c\bar {\iota }_*^{\alpha }$
orbit-width scaling is reflected in the fast-particle losses, we fit the losses to $c\bar {\iota }_*^{\alpha }$![]() for $\bar {\iota }_* \in [0.2,0.65]$
for $\bar {\iota }_* \in [0.2,0.65]$![]() , where the quasi-symmetry error is relatively constant. The fits and values of the coefficients are shown alongside the data in figure 4, for the $s=0.5$
, where the quasi-symmetry error is relatively constant. The fits and values of the coefficients are shown alongside the data in figure 4, for the $s=0.5$![]() and $s=0.7$
and $s=0.7$![]() results. The fits systematically overpredict the particle losses towards the higher end of the fitted range. Increasing the range of $\bar {\iota }_*$
results. The fits systematically overpredict the particle losses towards the higher end of the fitted range. Increasing the range of $\bar {\iota }_*$![]() in the fit to $[0.12,0.73]$
in the fit to $[0.12,0.73]$![]() changes of the values of the coefficients to ($c=0.07$
changes of the values of the coefficients to ($c=0.07$![]() , $\alpha =-0.99$
, $\alpha =-0.99$![]() ) and ($c=0.017$
) and ($c=0.017$![]() , $\alpha =-1.6$
, $\alpha =-1.6$![]() ) for the $s=0.7$
) for the $s=0.7$![]() and $s=0.5$
and $s=0.5$![]() fits, respectively, and does not significantly affect the agreement between the fitted curve and the data. Thus, the orbit width scaling with $\iota$
fits, respectively, and does not significantly affect the agreement between the fitted curve and the data. Thus, the orbit width scaling with $\iota$![]() only offers a qualitative estimate of how the fast-particle losses scale, and other mechanisms must be accounted for to get the full picture.
only offers a qualitative estimate of how the fast-particle losses scale, and other mechanisms must be accounted for to get the full picture.
Not included in the Simple calculations is the effect of the gyro-orbit about the guiding centres, which effectively widens the orbits and thus should increase the losses. As an estimate of the size of this effect, we calculate the ratio of the gyroradius to the orbit width, using the expression for the orbit width in the small-orbit-width limit given by Paul et al. (Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022):
where $\lambda = v_\perp ^2/(B v^2)$![]() , with $v_\perp$
, with $v_\perp$![]() the speed of the particle in the direction perpendicular to the magnetic field. For our QA configurations ($I\approx 0\ \mathrm {Tm}$
the speed of the particle in the direction perpendicular to the magnetic field. For our QA configurations ($I\approx 0\ \mathrm {Tm}$![]() , $G\approx 70\ \mathrm {Tm}$
, $G\approx 70\ \mathrm {Tm}$![]() , —$\boldsymbol {\nabla } \psi | \approx 20\ \mathrm {Tm}$
, —$\boldsymbol {\nabla } \psi | \approx 20\ \mathrm {Tm}$![]() , $N=0$
, $N=0$![]() , $M=1$
, $M=1$![]() ) this ratio ends up being roughly $\iota / 7$
) this ratio ends up being roughly $\iota / 7$![]() for $B\lambda = 0.5$
for $B\lambda = 0.5$![]() , and is thus much less than one. The finite gyro-orbit correction should thus be small for our range of $\iota$
, and is thus much less than one. The finite gyro-orbit correction should thus be small for our range of $\iota$![]() , except for the most deeply trapped particles. Specifically, the gyro-orbit width becomes larger than the orbit width for $B\lambda > (7/\iota )^2/[1 + (7/\iota )^2]$
, except for the most deeply trapped particles. Specifically, the gyro-orbit width becomes larger than the orbit width for $B\lambda > (7/\iota )^2/[1 + (7/\iota )^2]$![]() , or about $B\lambda > 0.987$
, or about $B\lambda > 0.987$![]() for the worst-case scenario of $\iota = 0.81$
for the worst-case scenario of $\iota = 0.81$![]() .
.
For configurations with this low quasi-symmetry error, collisional transport is almost surely dwarfed by turbulent transport. For example, ITG mode turbulence appears to dominate the heat transport in Wendelstein 7-X (Carralero et al. Reference Carralero, Estrada, Maragkoudakis, Windisch, Alonso, Beurskens, Bozhenkov, Calvo, Damm, Ford, Fuchert, García-Regaña, Pablant, Sánchez, Pasch and Velasco2021).
In figure 5, we show the maximum growth rates $\max {(\gamma )}$![]() for the $s=0.25$
for the $s=0.25$![]() surface in each configuration, as calculated from linear electrostatic gyrokinetic flux-tube simulations using the gyrokinetic code Stella (Barnes, Parra & Landreman Reference Barnes, Parra and Landreman2019) using adiabatic electrons. The simulations use gradients to promote ITG turbulence: $a/L_{Ti} = 3$
surface in each configuration, as calculated from linear electrostatic gyrokinetic flux-tube simulations using the gyrokinetic code Stella (Barnes, Parra & Landreman Reference Barnes, Parra and Landreman2019) using adiabatic electrons. The simulations use gradients to promote ITG turbulence: $a/L_{Ti} = 3$![]() and $a/L_{n} = 1$
and $a/L_{n} = 1$![]() . In the figure, $N_\alpha$
. In the figure, $N_\alpha$![]() indicates the number of flux tubes in which $\max {(\gamma )}$
indicates the number of flux tubes in which $\max {(\gamma )}$![]() was calculated, using equally spaced values of the field line label $\alpha _0$
was calculated, using equally spaced values of the field line label $\alpha _0$![]() on the interval $[0, {\rm \pi}]$
on the interval $[0, {\rm \pi}]$![]() , with a point always placed on $\alpha _0 = 0$
, with a point always placed on $\alpha _0 = 0$![]() . In Stella, $\alpha _0$
. In Stella, $\alpha _0$![]() (together with $s$
(together with $s$![]() ) specifies the location of a flux tube, with $\alpha _0$
) specifies the location of a flux tube, with $\alpha _0$![]() being the value of $\alpha = \theta - \iota \phi$
being the value of $\alpha = \theta - \iota \phi$![]() at the middle of the flux tube. The $\alpha _0$
at the middle of the flux tube. The $\alpha _0$![]() interval $[0, {\rm \pi}]$
interval $[0, {\rm \pi}]$![]() covers the entire half-period of a stellarator symmetric configuration. The simulations use $k_x=0$
covers the entire half-period of a stellarator symmetric configuration. The simulations use $k_x=0$![]() and the parallel domain extends for 70 toroidal turns, corresponding to about 8.4 poloidal turns for the lowest $\iota$
and the parallel domain extends for 70 toroidal turns, corresponding to about 8.4 poloidal turns for the lowest $\iota$![]() values. Due to the low shear of these configurations, the modes can have structure far along the field line; 70 toroidal turns was found to be sufficient to resolve this with good margins towards the boundaries for all configurations in the scan. The shear $\hat {s}$
values. Due to the low shear of these configurations, the modes can have structure far along the field line; 70 toroidal turns was found to be sufficient to resolve this with good margins towards the boundaries for all configurations in the scan. The shear $\hat {s}$![]() in each configuration at the radius of the simulations ($s=0.25$
in each configuration at the radius of the simulations ($s=0.25$![]() ) is shown in figure 6, revealing that most of the scan has a slight positive shear, with the configurations with $\bar {\iota } < 0.2$
) is shown in figure 6, revealing that most of the scan has a slight positive shear, with the configurations with $\bar {\iota } < 0.2$![]() having somewhat larger shear still below $0.1$
having somewhat larger shear still below $0.1$![]() . Note that while 0.1 is small in an absolute sense, it is not unusual for stellarators to have such low shear (Ascasíbar et al. Reference Ascasíbar2008). We only consider $k_x=0$
. Note that while 0.1 is small in an absolute sense, it is not unusual for stellarators to have such low shear (Ascasíbar et al. Reference Ascasíbar2008). We only consider $k_x=0$![]() modes, since these modes usually have the largest growth rates for ITG turbulence, which we confirmed for the $\bar {\iota } = 0.49$
modes, since these modes usually have the largest growth rates for ITG turbulence, which we confirmed for the $\bar {\iota } = 0.49$![]() and $\bar {\iota } = 0.49$
and $\bar {\iota } = 0.49$![]() cases.
cases.

Figure 5. (a) Maximum growth rate at $s=0.25$![]() , for a different number $N_\alpha$
, for a different number $N_\alpha$![]() of flux tubes in each $\bar {\iota }$
of flux tubes in each $\bar {\iota }$![]() configuration. Data are from electrostatic linear Stella simulations with $a/L_{T} = 3$
configuration. Data are from electrostatic linear Stella simulations with $a/L_{T} = 3$![]() , $a/L_n = 1$
, $a/L_n = 1$![]() and adiabatic electrons. (b) The $k_y$
and adiabatic electrons. (b) The $k_y$![]() mode number of the fastest growing mode. The underlying $\gamma (k_y)$
mode number of the fastest growing mode. The underlying $\gamma (k_y)$![]() curves are shown in figure 7. Vertical dotted lines indicate some low-order rationals.
curves are shown in figure 7. Vertical dotted lines indicate some low-order rationals.

Figure 6. Shear $\hat {s} = -({s}/{\iota }) ({{\mathrm {d}} \iota }/{{\mathrm {d}} s})$![]() at $s=0.25$
at $s=0.25$![]() plotted against the $\bar {\iota }$
plotted against the $\bar {\iota }$![]() of each equilibrium. Zero shear is marked with a dashed line.
of each equilibrium. Zero shear is marked with a dashed line.
The $\gamma (k_y)$![]() curves corresponding to the flux tube with the maximum growth rates are shown in figure 7, for some of the $\bar {\iota }_*$
curves corresponding to the flux tube with the maximum growth rates are shown in figure 7, for some of the $\bar {\iota }_*$![]() configurations. Despite some of the curves being calculated on flux tubes with different $\alpha _0$
configurations. Despite some of the curves being calculated on flux tubes with different $\alpha _0$![]() , the result is an essentially smooth change in the growth rate curves with $\bar {\iota }_*$
, the result is an essentially smooth change in the growth rate curves with $\bar {\iota }_*$![]() . For $\bar {\iota }_* \ge 0.77$
. For $\bar {\iota }_* \ge 0.77$![]() , the growth rate peaks above $\rho k_y = 3.0$
, the growth rate peaks above $\rho k_y = 3.0$![]() , so these simulations were modified to include higher $k_y$
, so these simulations were modified to include higher $k_y$![]() values.
values.

Figure 7. Growth rates $\gamma (k_y)$![]() for the flux tube with the highest $\max {(\gamma )}$
for the flux tube with the highest $\max {(\gamma )}$![]() for a subset of the different $\bar {\iota }_*$
for a subset of the different $\bar {\iota }_*$![]() configurations. The curves for different configurations are grouped into different panels based on the range of their $\bar {\iota }_*$
configurations. The curves for different configurations are grouped into different panels based on the range of their $\bar {\iota }_*$![]() values: (a) 0.13–0.34, (b) 0.37–0.56 and (c) 0.59–0.77. Colours indicate the specific $\bar {\iota }_*$
values: (a) 0.13–0.34, (b) 0.37–0.56 and (c) 0.59–0.77. Colours indicate the specific $\bar {\iota }_*$![]() corresponding to each curve.
corresponding to each curve.
Figures 5 and 7 both show a clear trend towards higher $\max {(\gamma )}$![]() and higher wavenumbers $k_y$
and higher wavenumbers $k_y$![]() with increasing $\bar {\iota }$
with increasing $\bar {\iota }$![]() , suggesting smaller-scale turbulence. At certain values of $\bar {\iota }$
, suggesting smaller-scale turbulence. At certain values of $\bar {\iota }$![]() , the ${N_{\alpha 0} =1}$
, the ${N_{\alpha 0} =1}$![]() and $N_{\alpha 0} =2$
and $N_{\alpha 0} =2$![]() curves in figure 5 display sharp dips towards lower $\max {(\gamma )}$
curves in figure 5 display sharp dips towards lower $\max {(\gamma )}$![]() .
.
This can be understood in terms of the flux tubes on rational surfaces not sampling the full flux-surface geometry. As a result, modes on different flux tubes will, for example, experience different levels of finite-Larmor-radius (FLR) damping in regions of bad curvature. This is illustrated in figure 8, which shows the value of $|\boldsymbol {\nabla } \alpha |^2$![]() at maxima in the curvature drift along the flux tube, for different flux tubes in the $\bar {\iota }_* = 0.49$
at maxima in the curvature drift along the flux tube, for different flux tubes in the $\bar {\iota }_* = 0.49$![]() and $\bar {\iota }_* = 0.50$
and $\bar {\iota }_* = 0.50$![]() geometries. For the non-rational $\iota$
geometries. For the non-rational $\iota$![]() , all flux tubes sample regions of bad curvature with all values of $|\boldsymbol {\nabla } \alpha |^2$
, all flux tubes sample regions of bad curvature with all values of $|\boldsymbol {\nabla } \alpha |^2$![]() , while for the rational $\iota$
, while for the rational $\iota$![]() , the different flux tubes display different values of $|\boldsymbol {\nabla } \alpha |^2$
, the different flux tubes display different values of $|\boldsymbol {\nabla } \alpha |^2$![]() at regions of bad curvature. Flux tubes with lower $|\boldsymbol {\nabla } \alpha |^2$
at regions of bad curvature. Flux tubes with lower $|\boldsymbol {\nabla } \alpha |^2$![]() in bad-curvature regions have higher growth rates as they experience less FLR damping.
in bad-curvature regions have higher growth rates as they experience less FLR damping.

Figure 8. Values of $|\boldsymbol {\nabla } \alpha |^2$![]() at points of maximum curvature drift along different flux tubes (given by $\alpha _0$
at points of maximum curvature drift along different flux tubes (given by $\alpha _0$![]() on the $x$
on the $x$![]() axis) for an irrational ($\bar {\iota }_* = 0.49$
axis) for an irrational ($\bar {\iota }_* = 0.49$![]() ) and rational ($\bar {\iota }_* = 0.50$
) and rational ($\bar {\iota }_* = 0.50$![]() ) flux surface.
) flux surface.
Figure 9 shows the corresponding nonlinear ion heat flux as calculated using the gyrokinetic code GX. GX is a new gyrokinetic code that runs on GPUs (Mandell, Dorland & Landreman Reference Mandell, Dorland and Landreman2018; Mandell et al. Reference Mandell, Dorland, Abel, Gaur, Kim, Martin and Qian2022). GX has been benchmarked against Stella and other established gyrokinetic codes (Mandell et al. Reference Mandell, Dorland, Abel, Gaur, Kim, Martin and Qian2022), and should be faster than Stella when it comes to running electrostatic nonlinear gyrokinetic simulations with adiabatic electrons. In contrast to the linear results, there is more variation between flux tubes with different $\alpha _0$![]() , but seemingly no great difference between rational and irrational values of $\iota$
, but seemingly no great difference between rational and irrational values of $\iota$![]() . Both these features are consistent with the nonlinear heat flux being insensitive to structures that are very elongated along the field line, so that even on irrational flux tubes, the turbulence does not effectively sample all regions of bad curvature on the flux surface. The trend with respect to $\iota$
. Both these features are consistent with the nonlinear heat flux being insensitive to structures that are very elongated along the field line, so that even on irrational flux tubes, the turbulence does not effectively sample all regions of bad curvature on the flux surface. The trend with respect to $\iota$![]() is non-monotonic with several local maxima and minima.
is non-monotonic with several local maxima and minima.

Figure 9. Nonlinear ion heat fluxes $Q_i$![]() for a few different $\bar {\iota }_*$
for a few different $\bar {\iota }_*$![]() configurations starting from $\bar {\iota }_*=0.20$
configurations starting from $\bar {\iota }_*=0.20$![]() to $\bar {\iota }_*=0.80$
to $\bar {\iota }_*=0.80$![]() . The fluxes are calculated using the gyrokinetic code GX on a single flux tube, with calculations done for the $\alpha _0 = 0$
. The fluxes are calculated using the gyrokinetic code GX on a single flux tube, with calculations done for the $\alpha _0 = 0$![]() and $\alpha _0={\rm \pi} /4$
and $\alpha _0={\rm \pi} /4$![]() flux tubes. Here $Q_{gB} = n_i T_i v_{Ti}^3/(B^2 a^2)$
flux tubes. Here $Q_{gB} = n_i T_i v_{Ti}^3/(B^2 a^2)$![]() , where $v_{Ti} = \sqrt {2T_i/m_i}$
, where $v_{Ti} = \sqrt {2T_i/m_i}$![]() is defined with a $\sqrt {2}$
is defined with a $\sqrt {2}$![]() unlike in the raw GX output.
unlike in the raw GX output.
We also investigated how far away coils can be placed from our plasma, using the method in Kappel et al. (Reference Kappel, Landreman and Malhotra2024). Given a maximum surface-current density $K_{\max }$![]() (corresponding to a minimum coil–coil distance) and a required accuracy in reproducing the last-closed flux surface of a target configuration, the distance between the plasma and the coil winding surface in the coil-shape code Regcoil (Landreman Reference Landreman2017) is increased until the maximum current density on the winding surface reaches $K_{\max }$
(corresponding to a minimum coil–coil distance) and a required accuracy in reproducing the last-closed flux surface of a target configuration, the distance between the plasma and the coil winding surface in the coil-shape code Regcoil (Landreman Reference Landreman2017) is increased until the maximum current density on the winding surface reaches $K_{\max }$![]() . The accuracy with which the coils produce the target last-closed flux surface is measured by
. The accuracy with which the coils produce the target last-closed flux surface is measured by

where the surface integrals are over the target surface and $\boldsymbol {n}$![]() is the unit normal of this surface; $\boldsymbol {B}$
is the unit normal of this surface; $\boldsymbol {B}$![]() is here the magnetic field produced by the coils.
is here the magnetic field produced by the coils.
The results of Regcoil calculations with $K_{\max }=17.16\ \mathrm {MA}\ \mathrm {m}^{-1}$![]() and $B_{n,\textrm {RMS}} = 0.01\ \mathrm {T}$
and $B_{n,\textrm {RMS}} = 0.01\ \mathrm {T}$![]() for the different $\bar {\iota }_*$
for the different $\bar {\iota }_*$![]() target configurations are shown in figure 10. All target configurations have been rescaled to the ARIES-CS minor radius $a$
target configurations are shown in figure 10. All target configurations have been rescaled to the ARIES-CS minor radius $a$![]() and volume-averaged $B$
and volume-averaged $B$![]() , and the value of $K_{\max }$
, and the value of $K_{\max }$![]() was chosen to match the minimum coil–coil distance of the ARIES-CS coil set.
was chosen to match the minimum coil–coil distance of the ARIES-CS coil set.

Figure 10. Coil–plasma separation for the different $\bar {\iota }_*$![]() configurations, calculated using Regcoil, alongside the magnetic scale length $L_{\|\boldsymbol {\nabla } B\|}$
configurations, calculated using Regcoil, alongside the magnetic scale length $L_{\|\boldsymbol {\nabla } B\|}$![]() . The configurations have been scaled up to $a=1.704 \mathrm {m}$
. The configurations have been scaled up to $a=1.704 \mathrm {m}$![]() and volume-average magnetic field of $5.865\ \mathrm {T}$
and volume-average magnetic field of $5.865\ \mathrm {T}$![]() , to match ARIES-CS. The sheet current density is computed to meet a target accuracy $B_{n,\textrm {RMS}} = 0.01\ \mathrm {T}$
, to match ARIES-CS. The sheet current density is computed to meet a target accuracy $B_{n,\textrm {RMS}} = 0.01\ \mathrm {T}$![]() and a maximum current density of $17.16\ \mathrm {MA}\ \mathrm {m}^{-1}$
and a maximum current density of $17.16\ \mathrm {MA}\ \mathrm {m}^{-1}$![]() , which corresponds to the minimum coil–coil distance of ARIES-CS (Kappel, Landreman & Malhotra Reference Kappel, Landreman and Malhotra2024).
, which corresponds to the minimum coil–coil distance of ARIES-CS (Kappel, Landreman & Malhotra Reference Kappel, Landreman and Malhotra2024).
Also included in the figure is the gradient scale length of $B$![]() , defined as
, defined as

where $\|\boldsymbol {\nabla } \boldsymbol {B} \|_{F}$![]() is the Frobenius norm of the tensor $\boldsymbol {\nabla } \boldsymbol {B}$
is the Frobenius norm of the tensor $\boldsymbol {\nabla } \boldsymbol {B}$![]() and the minimum is taken over boundary surface of the plasma. This metric, which is purely defined in terms of the target magnetic field and requires no coil geometry to calculate, has been proposed as a good proxy for the plasma–coil separation. Again, see Kappel et al. (Reference Kappel, Landreman and Malhotra2024) for details.
and the minimum is taken over boundary surface of the plasma. This metric, which is purely defined in terms of the target magnetic field and requires no coil geometry to calculate, has been proposed as a good proxy for the plasma–coil separation. Again, see Kappel et al. (Reference Kappel, Landreman and Malhotra2024) for details.
From figure 10, we see that the coil–plasma separation and gradient scale length both vary weakly over the $\iota$![]() scan. Specifically, the coil–plasma separation is between $2.85$
scan. Specifically, the coil–plasma separation is between $2.85$![]() and $3.25\ \mathrm {m}$
and $3.25\ \mathrm {m}$![]() with a minimum for $\bar {\iota }_*$
with a minimum for $\bar {\iota }_*$![]() around 0.35. The difference between the smallest plasma–coil separation and the largest is only $23\,\%$
around 0.35. The difference between the smallest plasma–coil separation and the largest is only $23\,\%$![]() of the minor radius. This is a small difference compared with the full range of plasma–coil separations present in Kappel et al. (Reference Kappel, Landreman and Malhotra2024). The $L_{\boldsymbol {\nabla } B}^*$
of the minor radius. This is a small difference compared with the full range of plasma–coil separations present in Kappel et al. (Reference Kappel, Landreman and Malhotra2024). The $L_{\boldsymbol {\nabla } B}^*$![]() metric is not expected to be a detailed enough proxy to fully capture such slight variations, which is reflected in the fact that $L_{\boldsymbol {\nabla } B}^*$
metric is not expected to be a detailed enough proxy to fully capture such slight variations, which is reflected in the fact that $L_{\boldsymbol {\nabla } B}^*$![]() does not reproduce the minimum at $\bar {\iota }_* = 0.35$
does not reproduce the minimum at $\bar {\iota }_* = 0.35$![]() .
.
We thus conclude that changes to $\bar {\iota }$![]() do not seem to play a large role in setting the plasma–coil separation. Since our configurations differ widely in their elongation, it also seems like elongation does not have a large effect on plasma–coil separation.
do not seem to play a large role in setting the plasma–coil separation. Since our configurations differ widely in their elongation, it also seems like elongation does not have a large effect on plasma–coil separation.
3.3. Varying shear in QA equilibrium
All configurations in the previous section have low values of global magnetic shear. This might make them susceptible to curvature-driven instabilities, compared with configurations with negative shear (Antonsen et al. Reference Antonsen, Drake, Guzdar, Hassam, Lau, Liu and Novakovskii1996; Nadeem, Rafiq & Persson Reference Nadeem, Rafiq and Persson2001).
High shear helps limiting the parallel extent of modes elongated along the magnetic field lines due to radially nearby field lines separating as the parallel coordinate is traversed, which forces such modes to have lower radial correlation length or a limited parallel extent. Gyrokinetic modes with smaller perpendicular extent generally have a smaller impact on a configuration, as they lead to less transport, which can be qualitatively understood by viewing the size of the mode perpendicular to the field line as a step length in a diffusive process (Merz & Jenko Reference Merz and Jenko2008).
We obtain configurations with stronger shear by additional optimizations where we add a term targeting the mean shear. Defining the mean shear as
where $c_1$![]() is the result of a linear fit $c_0+c_1 s$
is the result of a linear fit $c_0+c_1 s$![]() to the $\iota (s)$
to the $\iota (s)$![]() profile, we add the following optimization target to our objective (2.2):
profile, we add the following optimization target to our objective (2.2):
The negative sign in (3.5) is included to match the sign convention of the conventional definition of shear, $-({s}/{\iota })({{\mathrm {d}} \iota }/{{\mathrm {d}} s})$![]() .
.
Starting from the $\bar {\iota }_* = 0.42$![]() configuration found in § 3.2, which has a mean shear $\bar {\hat {s}} = 0.0195 \approx 0.02$
configuration found in § 3.2, which has a mean shear $\bar {\hat {s}} = 0.0195 \approx 0.02$![]() , we do two continuation scans in $\bar {\hat {s}}_*$
, we do two continuation scans in $\bar {\hat {s}}_*$![]() towards more negative and more positive shear, respectively, still targeting $\bar {\iota }_* = 0.42$
towards more negative and more positive shear, respectively, still targeting $\bar {\iota }_* = 0.42$![]() . The configurations with lowest and highest shear are shown in figure 11, alongside the $\bar {\hat {s}} = 0$
. The configurations with lowest and highest shear are shown in figure 11, alongside the $\bar {\hat {s}} = 0$![]() configuration.
configuration.

Figure 11. Plasma boundary shapes for select points in the scan ($\bar {\hat {s}}=-0.16$![]() , $\bar {\hat {s}}=0.0$
, $\bar {\hat {s}}=0.0$![]() and ${\bar {\hat {s}}=0.15}$
and ${\bar {\hat {s}}=0.15}$![]() ). Imposing positive shear mainly affects the triangularity of the boundary, while a negative shear makes the boundary more elongated and narrow.
). Imposing positive shear mainly affects the triangularity of the boundary, while a negative shear makes the boundary more elongated and narrow.
The resulting quasi-symmetry error is shown in figure 12. We see that imposing an additional shear objective degrades the quasi-symmetry. This is expected when adding competing objectives to an optimization problem.

Figure 12. Quasi-symmetry error (2.3) from a continuation scan varying shear. The scan is performed around the $\iota =0.42$![]() configuration.
configuration.
In figure 13, we show the fast-particle loss fraction calculated using the same set-up as for the $s=0.3$![]() calculations in figure 4. The degradation in quasi-symmetry appears to increase the fast-particle losses somewhat, but the effect is small enough for this range of shear for the uncertainty in the individual calculations to be comparable, as seen by the non-smoothness of the curve.
calculations in figure 4. The degradation in quasi-symmetry appears to increase the fast-particle losses somewhat, but the effect is small enough for this range of shear for the uncertainty in the individual calculations to be comparable, as seen by the non-smoothness of the curve.

Figure 13. Fast-particle loss fraction for the different $\bar {\hat {s}}$![]() configurations as calculated by Simple using the same simulation set-up as for the $s=0.3$
configurations as calculated by Simple using the same simulation set-up as for the $s=0.3$![]() curve in figure 4.
curve in figure 4.
Finally, we investigate the effect of shear on turbulent transport. The maximum growth rates $\max {(\gamma )}$![]() and the dependence of the growth rate on $k_y$
and the dependence of the growth rate on $k_y$![]() for the shear scan are shown in figures 14 and 15, respectively. We see a clear trend towards increasing maximum growth rates for shear above $\bar {\hat {s}} > 0.085$
for the shear scan are shown in figures 14 and 15, respectively. We see a clear trend towards increasing maximum growth rates for shear above $\bar {\hat {s}} > 0.085$![]() . This increase seems to be due to some new mode appearing at high $k_y$
. This increase seems to be due to some new mode appearing at high $k_y$![]() values, and the maximum growth rate of this mode is not properly resolved in these simulations. The mode remains even when setting the density gradient to zero, and must thus be driven by the ITG, although it appears at much larger values of $k_y$
values, and the maximum growth rate of this mode is not properly resolved in these simulations. The mode remains even when setting the density gradient to zero, and must thus be driven by the ITG, although it appears at much larger values of $k_y$![]() than typical ITG turbulence.
than typical ITG turbulence.

Figure 14. Maximum growth rates for the different $\bar {\hat {s}}$![]() configurations, using the same simulation set-up as in figure 5.
configurations, using the same simulation set-up as in figure 5.

Figure 15. Growth rates $\gamma (k_y)$![]() for a subset of the different $\bar {\hat {s}}_*$
for a subset of the different $\bar {\hat {s}}_*$![]() configurations.
configurations.
The effect on the nonlinear ion heat flux is more modest, but there is an increase of about $25\,\%$![]() for positive shear, as seen in figure 16. Positive shear being destabilizing is well known in the tokamak literature (Antonsen et al. Reference Antonsen, Drake, Guzdar, Hassam, Lau, Liu and Novakovskii1996; Nadeem et al. Reference Nadeem, Rafiq and Persson2001), and our results appear to be consistent with that.
for positive shear, as seen in figure 16. Positive shear being destabilizing is well known in the tokamak literature (Antonsen et al. Reference Antonsen, Drake, Guzdar, Hassam, Lau, Liu and Novakovskii1996; Nadeem et al. Reference Nadeem, Rafiq and Persson2001), and our results appear to be consistent with that.

Figure 16. Nonlinear heat fluxes for the different $\bar {\hat {s}}$![]() configurations.
configurations.
4. Conclusions
We have used a continuation method to generate a sequence of QA equilibria with different rotational transform profiles. The configurations are similar to each other, with each a local minimum of an optimization problem that is initialized at the previously found minimum. Through this procedure, we have found $n_{\textrm {fp}} = 2$![]() QA configurations with higher mean rotational transform $\bar {\iota }$
QA configurations with higher mean rotational transform $\bar {\iota }$![]() than what was previously found. We find QA configurations with exceptionally low quasi-symmetry errors for $\bar {\iota } \in [0.2, 0.65]$
than what was previously found. We find QA configurations with exceptionally low quasi-symmetry errors for $\bar {\iota } \in [0.2, 0.65]$![]() . For $\bar {\iota }$
. For $\bar {\iota }$![]() in and slightly above this range, increasing $\bar {\iota }$
in and slightly above this range, increasing $\bar {\iota }$![]() increases the elongation of the plasma boundary, which is likely what ultimately limits the achievable values of $\bar {\iota }$
increases the elongation of the plasma boundary, which is likely what ultimately limits the achievable values of $\bar {\iota }$![]() . Fast-particle losses as calculated by a collisionless drift-kinetic particle-tracing code decrease with $\iota$
. Fast-particle losses as calculated by a collisionless drift-kinetic particle-tracing code decrease with $\iota$![]() up to a point, but the effect is weaker than the $\iota ^{-1}$
up to a point, but the effect is weaker than the $\iota ^{-1}$![]() scaling predicted by purely accounting for how the orbit width scales with $\iota$
scaling predicted by purely accounting for how the orbit width scales with $\iota$![]() . Nevertheless, there is a potential conflict between having low elongation and low fast-particle losses. The dependence of the turbulent ion heat flux is non-monotonic in $\iota$
. Nevertheless, there is a potential conflict between having low elongation and low fast-particle losses. The dependence of the turbulent ion heat flux is non-monotonic in $\iota$![]() and shows some mild sensitivity to which flux tube the simulations are performed at. The linearly calculated growth rates, on the other hand, are sensitive to the choice of flux tube on rational flux surfaces.
and shows some mild sensitivity to which flux tube the simulations are performed at. The linearly calculated growth rates, on the other hand, are sensitive to the choice of flux tube on rational flux surfaces.
Higher shear can be imposed on the configurations by adding an extra term in the objective function. This increases the quasi-symmetry error somewhat, but this hardly affects the fast-particle losses. The turbulent heat flux tends to increase somewhat for positive shear, causing an increases by about $25\,\%$![]() for the range of shear considered here. The effect of shear in magnetohydrodynamic stability is likely even more important, but was not considered here.
for the range of shear considered here. The effect of shear in magnetohydrodynamic stability is likely even more important, but was not considered here.
Acknowledgements
The authors are grateful for discussions with B. Dorland, I. Abel, R. Jorge, E. Rodriguez, W. Sengupta, N. Nikulsin, R. Nies, T. Adkins and J. Parisi, who have all provided valuable input and motivation for this work.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the US Department of Energy, Office of Science, Office of Fusion Energy Science, under award number DE-FG02-93ER54197. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a US Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231 using NERSC award FES-ERCAP-mp217-2023. Additional computations were performed on the HPC systems Cobra and Raven at the Max Planck Computing and Data Facility (MPCDF).
Declaration of interest
The authors report no conflict of interest.