Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T22:22:14.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Ripple modifications to alpha transport in tokamaks

Published online by Cambridge University Press:  02 November 2018

Peter J. Catto
Peter J. Catto*
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: catto@psfc.mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Magnetic field ripple is inherent in tokamaks since the toroidal magnetic field is generated by a finite number of toroidal field coils. The field ripple results in departures from axisymmetry that cause radial transport losses of particles and heat. These ripple losses are a serious concern for alphas near their birth speed 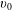$v_{0}$ since alpha heating of the background plasma is required to make fusion reactors into economical power plants. Ripple in tokamaks gives rise to at least two alpha transport regimes of concern. As the slowing down time 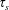$\unicode[STIX]{x1D70F}_{s}$ is much larger than the time for an alpha just born to make a toroidal transit, a regime referred to as the 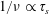$1/\unicode[STIX]{x1D708}\propto \unicode[STIX]{x1D70F}_{s}$ regime can be encountered, with $\unicode[STIX]{x1D708}$ the appropriate alpha collision frequency. In this regime the radial transport losses increase as 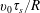$v_{0}\unicode[STIX]{x1D70F}_{s}/R$, with 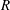$R$ the major radius of the tokamak. The deleterious effect of ripple transport is mitigated by electric and magnetic drifts within the flux surface. When drift tangent to the flux surface becomes significant another ripple regime, referred to as the 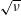$\sqrt{\unicode[STIX]{x1D708}}$ regime, is encountered where a collisional boundary layer due to the drift plays a key role. We evaluate the alpha transport in both regimes, taking account of the alphas having a slowing down rather than a Maxwellian distribution function and their being collisionally scattered by a collision operator appropriate for alphas. Alpha ripple transport is found to be in the 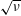$\sqrt{\unicode[STIX]{x1D708}}$ regime where it will be a serious issue for typical tokamak reactors as it will be well above the axisymmetric neoclassical level and can be large enough to deplete the alpha slowing down distribution function unless toroidal rotation is strong.

Keywords

fusion plasmaplasma confinement
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 5 , October 2018 , 905840508
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boozer, A. H. 1980 Guiding center drift equations. Phys. Fluids 23, 904–908.Google Scholar
Boozer, A. H. 1981 Plasma equilibrium with rational magnetic surfaces. Phys. Fluids 24, 1999–2003.Google Scholar
Calvo, I., Parra, F. I., Alonso, J. A. & Velasco, J. L. 2014 Optimizing stellarators for large flows. Plasma Phys. Control. Fusion 56, 094003; 11pp.Google Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2013 Stellarators close to quasisymmetry. Plasma Phys. Control. Fusion 55, 125014; 28pp.Google Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2017 The effect of tangential drifts on neoclassical transport in stellarators close to omnigeneity. Plasma Phys. Control. Fusion 59, 055014; 19pp.Google Scholar
Catto, P. J. 1988 Slowing down tail enhancement of the neoclassical energy flux of $\unicode[STIX]{x1D6FC}$ ’s. Phys. Rev. Lett. 60, 1954–1957.Google Scholar
Catto, P. J., Parra, F. I. & Pusztai, I. 2017 Electromagnetic zonal flow residual responses. J. Plasma Phys. 83, 905830402; 38pp.Google Scholar
Connor, J. W. & Hastie, R. J. 1973 Neoclassical diffusion arising from magnetic field ripples in tokamaks. Nucl. Fusion 13, 221–225.Google Scholar
Cordey, J. G. 1976 Effects of trapping on the slowing-down of fast ions in a toroidal plasma. Nucl. Fusion 16, 499–507.Google Scholar
Davidson, J. N. 1976 Effect of toroidal field ripple on particle and energy transport in a tokamak. Nucl. Fusion 16, 731–742.Google Scholar
Galeev, A. A., Sagdeev, R. Z., Furth, H. P. & Rosenbluth, M. N. 1969 Plasma diffusion in a toroidal stellarator. Phys. Rev. Lett. 22, 511–514.Google Scholar
Goldston, R. J., White, R. B. & Boozer, A. H. 1981 Confinement of high-energy trapped particles in tokamaks. Phys. Rev. Lett. 47, 647–649.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 2007 Table of Integrals, Series, and Products, 7th edn p. 533. Elsevier/Academic.Google Scholar
Hazeltine, R. D. 1973 Recursive derivation of the drift-kinetic equation. Plasma Phys. 15, 77–80.Google Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77, 087001; 35pp.Google Scholar
Ho, D. D.-M. & Kulsrud, R. M. 1987 Neoclassical transport in stellarators. Phys. Fluids 30, 442–461.Google Scholar
Hsu, C. T., Catto, P. J. & Sigmar, D. J. 1990 Neoclassical transport of isotropic fast ions. Phys. Fluids B 2, 280; 11pp.Google Scholar
Kagan, G. & Catto, P. J. 2008 Arbitrary poloidal gyroradius effects in tokamak pedestals and transport barriers. Plasma Phys. Control. Fusion 50, 085010; 25pp.Google Scholar
Landreman, M. & Catto, P. J. 2012 Omnigenity as generalized quasisymmetry. Phys. Plasmas 19, 056103; 16pp.Google Scholar
Landreman, M. & Catto, P. J. 2013 Conservation of energy and mgnetic moment in neoclassical calculations for optimized stellarators. Plasma Phys. Control. Fusion 55, 095017; 17pp.Google Scholar
Linsker, R. & Boozer, A. H. 1982 Banana drift transport in tokamaks with ripple. Phys. Fluids 25, 143–147.Google Scholar
Nocentini, A., Tessarotto, M. & Engelmann, F. 1975 Neoclassical theory of collisional transport in the presence of fusion $\unicode[STIX]{x1D6FC}$ -particles. Nucl. Fusion 15, 359–370.Google Scholar
Parra, F. I. & Catto, P. J. 2008 Limitations of gyrokinetics on transport time scales. Plasma Phys. Control. Fusion 50, 065014; 23pp.Google Scholar
Parra, F. I. & Catto, P. J. 2009 Vorticity and intrinsic ambipolarity in turbulent tokamaks. Plasma Phys. Control. Fusion 51, 095008; 38pp.Google Scholar
Parra, F. I. & Catto, P. J. 2010 Transport of momentum in full $f$ gyrokinetics. Phys. Plasmas 17, 056106; 11pp.Google Scholar
Paul, E. J., Landreman, M., Poli, F. M., Spong, D. A., Smith, H. M. & Dorland, W. 2017 Rotation and neoclassical ripple transport in ITER. Nucl. Fusion 57, 116044; 14pp.Google Scholar
Stringer, T. E. 1972 Effect of the magnetic field ripple on diffusion in tokamaks. Nucl. Fusion 12, 689–694.Google Scholar
Tsang, K. T. 1977 Banana drift diffusion in a tokamak magnetic field with ripples. Nucl. Fusion 17, 557–563.Google Scholar