No CrossRef data available.
Article contents
Correction to “Simple r. e. degree structures”
Published online by Cambridge University Press: 12 March 2014
Extract
In the paper mentioned in the title (this Journal, vol. 52 (1987), pp. 208–213), it is shown that if 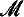 ⊨ “V = HC is recursively inaccessible” is ω-standard
⊨ “V = HC is recursively inaccessible” is ω-standard 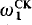 -nonstandard, then
-nonstandard, then 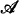 = s.p.(
= s.p.(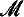 ) has at most four r. e. degrees. They are 0 = deg(∅),
) has at most four r. e. degrees. They are 0 = deg(∅), 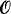 = deg{e ∣ We is a recursive well-ordering of ω},
= deg{e ∣ We is a recursive well-ordering of ω}, 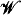 = deg{R ∣
= deg{R ∣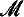 ⊨ “R codes a well-ordering”}, and
⊨ “R codes a well-ordering”}, and 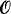 ∨
∨ 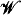 . Furthermore, 0 <
. Furthermore, 0 < 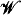 <
< 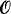 ∨
∨ 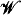 and 0 <
and 0 < 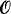 . Then it is claimed that
. Then it is claimed that 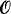 <
< 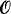 <
< 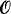 ∨
∨ 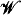 and
and 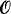 =
= 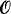 ∨
∨ 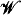 if are each possible. In fact,
if are each possible. In fact, 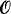 <
< 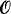 <
< 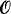 ∨
∨ 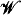 always.
always.
The mistake in the argument is that the model 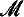 ≤T
≤T 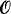 is really a structure on a set, which we may as well take as ω: there is an R ⊆ ω × ω, R ≤T
is really a structure on a set, which we may as well take as ω: there is an R ⊆ ω × ω, R ≤T 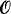 , and ‹ω, R› ≃
, and ‹ω, R› ≃ 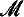 . So a copy of
. So a copy of 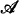 coded as a relation on ω is ≤
coded as a relation on ω is ≤ 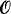 over
over 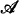 . But there is no reason to think that the restriction of the isomorphism of
. But there is no reason to think that the restriction of the isomorphism of 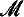 and ‹ω, R› to
and ‹ω, R› to 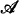 is Σ 1(
is Σ 1(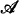 ).
).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988

