In this paper we present a normalization theorem for a natural deduction formulation of Zermelo set theory. Our result gets around M. Crabbe's counterexample to normalizability (Hallnäs [3]) by adding an inference rule of the form

and requiring that this rule be used wherever it is applicable. Alternatively, we can regard the result as pertaining to a modified notion of normalization, in which an inference

is never considered reducible if A is T Є T, even if R is an elimination rule and the major premise of R is the conclusion of an introduction rule. A third alternative is to regard (1) as a derived rule: using the general well-foundedness rule

we can derive (1). If we regard (2) as neutral with respect to the normality of derivations (i.e., (2) counts as neither an introduction nor an elimination rule), then the resulting proofs are normal.

i) We show for each context-free language L that by considering each word of L as a structure in a natural way, one turns L into a finite union of classes which satisfy a finitary analog of the characteristic properties of complete universal first order classes of structures equipped with elementary embeddings. We show this to hold for a much larger class of languages which we call free local languages, ii) We define local languages, a class of languages between free local and context-sensitive languages. Each local language L has a natural extension L ∞ to infinite words, and we prove a series of “pumping lemmas”, analogs for each local language L of the “uvxyz theorem” of context free languages: they relate the existence of large words in L or L ∞ to the existence of infinite “progressions” of words included in L, and they imply the decidability of various questions about L or L ∞. iii) We show that the pumping lemmas of ii) are independent from strong axioms, ranging from Peano arithmetic to ZF + Mahlo cardinals.

We hope that these results are useful for a model-theoretic approach to the theory of formal languages.

Dowker [1] raised the question of the existence of filters such that for every coloring (partition) of the underlying index set I with two colors there is a relation R on I which (i) is fat (in the sense that sets of the form {y Є I∣xRy} are in the filter) and (ii) has no bichromatic symmetric pairs (i.e., distinct indices x and y such that x R y and y R x). Additionally, he required that the filter have no anti-symmetric fat relation, for such a relation would vacuously satisfy (i) and (ii). The question of the existence of Dowker filters has been studied more recently by Rudin [3], [4], who conjectures [3] that such filters do not exist.

For ZFC the problem remains open. However, Example 2 of this paper shows that one can construct a Dowker filter provided one drops the axiom of choice in favor of the Baire Property (BP) axiom which is known to be incompatible with ZFC but relatively consistent with ZF. In fact, the filter constructed is super-Dowker in the sense that (ii) can be replaced by the requirement that all components of all symmetric pairs have the same color. But, in ZFC the existence of a super-Dowker filter implies the existence of a measurable cardinal.

Let F be a filter on an index set I. A set will be called big, small, or medium depending on whether F contains that set, its compliment, or neither, respectively. We define five cardinals associated with F:

α denotes the smallest cardinal such that there is a family of α big sets whose intersection is not big.

ν denotes the smallest cardinal such that there is a family of ν big sets whose intersection is small.

On June 4, 1925, Hilbert delivered an address to the Westphalian Mathematical Society in Miinster; that was, as a quick calculation will convince you, almost exactly sixty years ago. The address was published in 1926 under the title Über das Unendliche and is perhaps Hilbert's most comprehensive presentation of his ideas concerning the finitist justification of classical mathematics and the role his proof theory was to play in it. But what has become of the ambitious program for securing all of mathematics, once and for all? What of proof theory, the very subject Hilbert invented to carry out his program? The Hilbertian ambition reached out too far: in its original form, the program was refuted by Gödel's Incompleteness Theorems. And even allowing more than finitist means in metamathematics, the Hilbertian expectations for proof theory have not been realized: a constructive consistency proof for second-order arithmetic is still out of reach. (And since that theory provides a formal framework for analysis, it was considered by Hilbert and Bernays as decisive for proof theory.) Nevertheless, remarkable progress has been made. Two separate, but complementary directions of research have led to surprising insights: classical analysis can be formally developed in conservative extensions of elementary number theory; relative consistency proofs can be given by constructive means for impredicative parts of second order arithmetic. The mathematical and metamathematical developments have been accompanied by sustained philosophical reflections on the foundations of mathematics. This indicates briefly the main themes of the contributions to the symposium; in my introductory remarks I want to give a very schematic perspective, that is partly historical and partly systematic.

In this paper we solve some of Pál Erdős's favorite problems on uncountably chromatic graphs. Generalizing a finite graph theory result of Tutte, Erdős and R. Rado showed that for every infinite cardinal κ there exists a triangle-free, κ-chromatic graph of size κ. For κ = ℵ0, Erdős established the existence of ℵ0-chromatic graphs excluding even C4, C5,…, Cn, i.e. circuits up to a given length. For κ < ℵ0 the situation is different. As shown by Erdős and A. Hajnal, a graph is necessarily countably chromatic if it omits any finite bipartite graph. We can, however, exclude any finite list of nonbipartite graphs (this obviously reduces to excluding finitely many odd circuits). They posed an even stronger conjecture, namely, that similar examples must occur in every uncountably chromatic graph. To be specific, they conjectured that for every infinite κ, every κ-chromatic graph contains a κ-chromatic triangle-free subgraph. Here we show that this may not be true for κ = ℵ1 i.e. we exhibit a model where it is false. We must emphasize that the conjecture is probably false already in ZFC, but we have been unable to show this.

Alfred Tarski started contributing to set theory at a time when the Zermelo-Fraenkel axiom system was not yet fully formulated and as simple a concept as that of the inaccessible cardinal was not yet fully defined. At the end of Tarski's career the basic concepts of the three major areas and tools of modern axiomatic set theory, namely constructibility, large cardinals and forcing, were already clearly defined and were in the midst of a rapid successful development. The role of Tarski in this development was somewhat similar to the role of Moses showing his people the way to the Promised Land and leading them along the way, while the actual entry of the Promised Land was done mostly by the next generation. The theory of large cardinals was started mostly by Tarski, and developed mostly by his school. The mathematical logicians of Tarski's school contributed much to the development of forcing, after its discovery by Paul Cohen, and to a lesser extent also to the development of the theory of constructibility, discovered by Kurt Gödel. As in other areas of logic and mathematics Tarski's contribution to set theory cannot be measured by his own results only; Tarski was a source of energy and inspiration to his pupils and collaborators, of which I was fortunate to be one, always confronting them with new problems and pushing them to gain new ground.

Tarski's interest in set theory was probably aroused by the general emphasis on set theory in Poland after the First World War, and by the influence of Wactaw Sierpinski, who was one of Tarski's teachers at the University of Warsaw. The very first paper published by Tarski, [21], was a paper in set theory.

§0. Introduction. What follows is a write-up of my contribution to the symposium “Hilbert's Program Sixty Years Later” which was sponsored jointly by the American Philosophical Association and the Association for Symbolic Logic. The symposium was held on December 29,1985 in Washington, D. C. The panelists were Solomon Feferman, Dag Prawitz and myself. The moderator was Wilfried Sieg. The research which I discuss here was partially supported by NSF Grant DMS-8317874.

I am grateful to the organizers of this timely symposium on an important topic. As a mathematician I particularly value the opportunity to address an audience consisting largely of philosophers. It is true that I was asked to concentrate on the mathematical aspects of Hilbert's program. But since Hilbert's program is concerned solely with the foundations of mathematics, the restriction to mathematical aspects is really no restriction at all.

Hilbert assigned a special role to a certain restricted kind of mathematical reasoning known as finitistic. The essence of Hilbert's program was to justify all of set-theoretical mathematics by means of a reduction to finitism. It is now well known that this task cannot be carried out. Any such possibility is refuted by Gödel's theorem. Nevertheless, recent research has revealed the feasibility of a significant partial realization of Hilbert's program. Despite Gödel's theorem, one can give a finitistic reduction for a substantial portion of infinitistic mathematics including many of the best-known nonconstructive theorems. My purpose here is to call attention to these modern developments.

It follows constructively from weak versions of Markov's principle (MP) and of Church's thesis (WCT) that logical validity for single sentences is not arithmetically definable. This is a direct consequence of the constructive model-theoretic fact that, using MP and WCT, one can prove the categoricity of first-order Heyting arithmetic. By a straightforward refinement of this proof, we then obtain generalizations of the incompleteness theorem of Kreisel [K 2] as presented by van Dalen [Da] and improved by Leivant [L 1]. An analogous result for classical validity in r.e. models appears in [V].

Our methods of proof are new in that they rely not upon variants of the ideas of [K2] but upon a constructive proof idea inspired by the classical result of Tennenbaum ([Te], [E&K], [S]) on recursive models of arithmetic. This line of reasoning was suggested by the applications of readability to recursive mathematics described in [McC1], [McC2] and [McC3].

Tarski made a fundamental contribution to our understanding of R, perhaps mathematics’ most basic structure. His theorem is the following.

To any formula ϕ(X1, …, Xm) in the vocabulary {0, 1, +, ·, <} one can effectively associate two objects: (i) a quantifier free formula 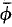(X 1, …, Xm ) in

(1) the same vocabulary, and (ii) a proof of the equivalence ϕ ↔ 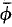that uses only the axioms for real closed fields. (Reminder: real closed fields are ordered fields with the intermediate value property for polynomials.)

Everything in (1) has turned out to be crucial: that arbitrary formulas are considered rather than just sentences, that the equivalence ϕ ↔ 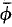holds in all real closed fields rather than only in R; even the effectiveness of the passage from ϕ to 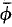has found good theoretical uses besides firing the imagination.

We begin this survey with some history in §1. In §2 we discuss three other influential proofs of Tarski's theorem, and in §3 we consider some of the remarkable and totally unforeseen ways in which Tarski's theorem functions nowadays in mathematics, logic and computer science.

I thank Ward Henson, and in particular Wilfrid Hodges without whose constant prodding and logistic support this article would not have been written.

The topic of this paper is jump operators, a subject which originated with some questions of Martin and a partial answer to them obtained by Steel [18]. The topic of jump operators is a part of the general study of the structure of the Turing degrees, but it is concerned with an aspect of that structure which is different from the usual concerns of classical recursion theory. Specifically, it is concerned with studying functions on the degrees, such as the Turing jump operator, the hyperjump operator, and the sharp operator.

Roughly speaking, a jump operator is a definable ≤T-increasing function on the Turing degrees. The purpose of this paper is to characterize the jump operators, in terms of concepts from descriptive set theory. Again roughly speaking, the main theorem states that all jump operators (other than the identity function) are obtained from pointclasses by the same process by which the hyperjump operator is obtained from the pointclass Π11; that is, if Γ is the pointclass, then the operator maps the real x to the universal Γ(x) subset of ω. This characterization theorem has some corollaries, one of which answers a question of Steel [18]. In §1 we give a brief introduction to this general topic, followed by a brief (and still somewhat imprecise) description of the results contained in this paper.

Markov's principle is more than a convenience in constructive arithmetic and analysis; it is absolutely essential to significant areas of constructive cardinal arithmetic. In turn, logical relations among intuitively appealing principles of constructive cardinal arithmetic parallel relations between MPS and other “problematic axioms” for constructive mathematics, such as the limited principle of omniscience. Finally, simple closure properties on the Dedekind finite sets provide ready examples of statements which are strictly weaker than Markov's principle and yet are independent of extensions of IZF.

MPS, Markov's principle with variables over sets, is equivalent to each of these elementary properties of ⊿, the class of Dedekind finite sets:

1. ∀A(A Є ⊿ ↔ CP(A)).

2. [*]A Є ⊿ ↔ ∀B (A + B is infinite ↔ B is infinite).

3. [**]A Є ⊿ ↔ ∀B((A + 1) x B is infinite ↔ B is infinite).

CP is Tarski's cancellation property. Consequently, MPS is tantamount, in constructive mathematics, to the standard classical characterizations of ⊿ in terms of cardinality.

[*] and [**] imply that ⊿ is closed under addition and multiplication. Closure under addition is, in turn, constructively equivalent to the closure of ⊿ under all combinatorial functions and to the fact that ⊿ is closed under each strict combinatorial function individually. Generally speaking, a function on P(ω) is combinatorial whenever it preserves finiteness, respects cardinality and has a “moduluslike” associate function. It is strict when it is strictly increasing relative to the subset ordering, [cf. §6 for precise definitions.] From this, we see that MPS is foundational for cardinal arithmetic on the constructive Dedekind finite sets.

In the Symposium on Hilbert's Program to which the following was contributed, I was asked to talk about the metamathematical aspects of Hilbert's Program (H.P.), while the other two speakers (Simpson and Prawitz) were to deal with the mathematical and philosophical aspects respectively. However, more so than for other foundational schemes, these three aspects of H.P., both as originally conceived and in its subsequent developments, are intimately linked.

Here I shall survey a body of proof-theoretical results stemming from H.P., but organized in a way that is closely tied to various reductive foundational aims, albeit going beyond those advanced by Hilbert. I believe this view of reductive proof-theory (not original with me) helps one to better understand what has been achieved thereby than other, more familiar accounts.

Any list of Alfred Tarski's achievements would mention his decision procedure for real-closed fields. He proved a number of other less publicized decidability results too. We shall survey these results. After surveying them we shall ask what Tarski had in mind when he proved them. Today our emphases and concepts are sometimes different from those of Tarski in the early 1930s. Some of these changes are the direct result of Tarski's own fundamental work in model theory during the intervening years.

Tarski's work on decidable theories is important not just for the individual decidability theorems themselves. His method for all these decidability results was elimination of quantifiers, and he systematically used this method to prove a range of related theorems about completeness and definability. He also led several of his students to do important work using this same method. Tarski's use of quantifier elimination has had a deep and cumulative influence on model theory and the logical treatment of algebraic theories.

We thank Solomon Feferman, Steven Givant, Haragauri Gupta, Yuri Gurevich. Angus Macintyre, Gregory Moore, Robert Vaught and the referee for helpful discussions and comments. Also we thank Madame Maria Mostowska and Roman Murawski for sending us material from Polish libraries.

The aim of this paper is to characterize varieties of Heyting algebras with decidable theory of their finite members. Actually we prove that such varieties are exactly the varieties generated by linearly ordered algebras. It contrasts to the result of Burris [2] saying that in the case of whole varieties, only trivial variety and the variety of Boolean algebras have decidable first order theories.

In this essay we discuss Tarski's work on what he called the methodology of the deductive sciences, or more briefly, borrowing the terminology of Hilbert, metamathematics, The clearest statement of Tarski's views on this subject can be found in his textbook Introduction to logic [41m].1 Here he describes the tasks of metamathematics as “the detailed analysis and critical evaluation of the fundamental principles that are applied in the construction of logic and mathematics”. He goes on to describe what these fundamental principles are: All the expressions of the discipline under consideration must be defined in terms of a small group of primitive expressions that seem immediately understandable. Furthermore, only those statements of the discipline are accepted as valid that can be deduced by precisely defined and universally accepted means from a small set of axioms whose validity seems evident. The method of constructing a discipline in strict accordance with these principles is known as the deductive method, and the disciplines constructed in this manner are called deductive systems. Since contemporary mathematical logic is one of those disciplines that are subject to these principles, it itself is a deductive science. Tarski then goes on to say:

This identification of mathematics with the deductive sciences is in our view one of the distinctive aspects of Tarski's work. Another characteristic feature is his broad view of what constitutes the domain of metamathematical investigations. A clue to this aspect of his work can also be found in Chapter 6 of Introduction to logic . After a discussion of the notions of completeness and consistency, he remarks that the investigations concerning these topics were among the most important factors contributing to a considerable extension of the domain of methodological studies, and caused even a fundamental change in the whole character of the methodology of deductive sciences.

This is a continuation of Believing the axioms. I, in which nondemonstrative arguments for and against the axioms of ZFC, the continuum hypothesis, small large cardinals and measurable cardinals were discussed. I turn now to determinacy hypotheses and large large cardinals, and conclude with some philosophical remarks.

Determinacy is a property of sets of reals. If A is such a set, we imagine an infinite game G(A) between two players I and II. The players take turns choosing natural numbers. In the end, they have generated a real number r (actually a member of the Baire space ωω). If r is in A, I wins; otherwise, II wins. The set A is said to be determined if one player or the other has a winning strategy (that is, a function from finite sequences of natural numbers to natural numbers that guarantees the player a win if he uses it to decide his moves).

Determinacy is a “regularity” property (see Martin [1977, p. 807]), a property of well-behaved sets, that implies the more familiar regularity properties like Lebesgue measurability, the Baire property (see Mycielski [1964] and [1966], and Mycielski and Swierczkowski [1964]), and the perfect subset property (Davis [1964]). Infinitary games were first considered by the Polish descriptive set theorists Mazur and Banach in the mid-30s; Gale and Stewart [1953] introduced them into the literature, proving that open sets are determined and that the axiom of choice can be used to construct an undetermined set.

We show that if κ is an inaccessible cardinal then P κλ splits into λ<κ many disjoint stationary subsets. We also show that if P κλ carries a strongly saturated ideal then the nonstationary ideal cannot be λ+-saturated.

We combine two techniques of set theory relating to mininal degrees of constructibility. Jensen constructed a minimal real which is additionally a singleton. Groszek built an initial segment of order type 1 + α*, for any ordinal α. This paper shows how to force a singleton such that the c-degrees beneath it, all represented by reals, are of type 1 + α*, for many ordinals α. We also examine the definability α needs to be so represented by a real.