Provability of the pigeonhole principle and the existence of infinitely many primes

Extract

In this note we shall be interested in the following problems.

Problem 1. Can IΔ₀ ⊢ ∀x∃y > x(y is prime)?

Here I Δ₀ is Peano arithmetic with the induction axiom restricted to bounded (i.e. Δ₀) formulae.

Problem 2. Can IΔ₀ ⊢ Δ₀ PHP?

Here Δ₀ PHP (Δ₀ pigeonhole principle) is the schema

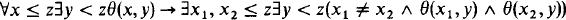
for θ ∈ Δ₀, or equivalently in IΔ₀, for a Δ₀ formula F(x,y)

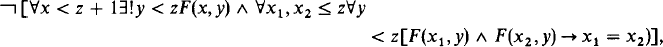
written .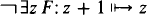

By obtaining partial solutions to Problem 2 we shall show that Problem 1 has a positive solution if IΔ₀ is replaced by IΔ₀ + ∀xx ^log(x) exists.

Our notation will be entirely standard (see for example [3] and [4]). In particular all logarithms will be to the base 2 and in expressions like log(x), (1 + ε)x, etc. we shall always mean the integer part of these quantities.

Concerning Problem 2 we remark that it is shown in [5] that for k ∈ N and F ∈ Δ₀,

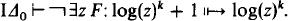
As far as we know this is the best result of this form, in that we do not know how to replace log(z) ^k by anything larger. However, as we shall show in Theorem 1, we can do much better if we increase the difference between the sizes of the domain and range of F.

In what follows let M be a countable nonstandard model of IΔ₀, and let 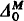be those subsets of M defined by Δ₀ formulae with parameters from M.

Theorem 1. For k ∈ N and F ∈ Δ₀,

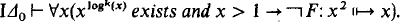
Here log⁰(x) = x, log ^{k + 1}(x) = log(log ^k (x)).

Proof. To simplify matters, consider first the case k = 1. So assume M ⊨ a ^log(a) exists and 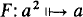with 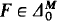and a > 1. The idea of the proof is the following.