Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shelah, Saharon
1987.
Classification Theory.
Vol. 1292,
Issue. ,
p.
264.

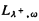 by adding a suitable predicate in more than
by adding a suitable predicate in more than 