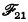At the end of his paper [2], Silver shows how methods developed by Jensen and Solovay in order to prove results about the constructible universe L may be adapted to prove corresponding results for the universe L[μ], where μ is a normal measure on some uncountable cardinal ρ. In this paper we pursue this in greater depth. Jensen proved, in fact, much stronger results than those considered in [2], and we shall show that all of these carry over from L to L[μ], More precisely, we show that if V = L[μ] is assumed, then for any regular uncountable cardinal κ and any uncountable λ < κ, + (κ, λ) holds, and that + (κ, κ) holds just in the case κ is not ineffable. This result was proved to hold in L by Jensen, who first formulated the principles + (κ, λ).

Our proof differs in detail from Jensen's, and at one point (in choosing the set B of + ) differs fundamentally from his argument. However, the fact remains that our argument is modelled closely upon Jensen's, and it should be made clear that in many parts it is a straightforward adaption of his proof to the L[μ] situation. It is regrettable that, at the time of our writing this, Jensen's proof still only exists in the rough, handwritten form of [1]; so we shall give our argument in some detail, even those parts which are merely “translations” of Jensen's original arguments.

This paper presents three generalizations of the Second Incompleteness Theorem of Gödel (see [2]) which apply to a broader class of formal systems than previous generalizations (as, e.g., the generalization in [1]).

The content of all three of our results is that it is versions of the third derivability condition of Hilbert and Bernays (see p. 286 of [3]) which are crucial to Gödel's theorem. The second derivability condition plays some role in certain logics, but even there, only in the far weaker form of a definability condition (see Theorem 2).

The elimination of the first derivability condition allows the application of the Consistency Theorem to cut-free logics which cannot prove that they are closed under cut.

It is Theorem 1 which will probably have primary interest for readers who are not concerned with technical proof theory or with foundations, for it treats logics with quantifiers, and in that case one can dispose entirely of the first and second derivability conditions. The derivation of this result requires a “new twist” on old arguments. Specifically, we use a new variation on the standard self-referential lemma (this is Lemma 5.1 of [l]) to obtain a somewhat different self-referential construction than has previously been employed (this is our lemma in §2 below). With this new construction, we consider the sentence φ which “expresses” the fact: “My negation is provable.” Then, using hypotheses associated with Gödel's First Incompleteness Theorem, one shows that ⊢¬φ is impossible in a consistent logic. Finally, using only a version of the third Hilbert-Bernays derivability condition, one shows that the provability of the consistency statement implies ⊢¬φ, and hence that consistency is unprovable.

By an elementary condition in the variablesx1, …, xn, we mean a conjunction of the form x1 ≤ i < j ≤ naij where each aij is one of the formulas xi = xj or xi ≠ xj. (We should add that the formula x1 = x1 should be regarded as an elementary condition in the one variable x1.)

Clearly, according to this definition, some elementary conditions are inconsistent, some are consistent. For instance (in the variables x1, x2, x3) the conjunction x1 = x2 & x1 = x3 & x2 ≠ x3 is inconsistent.

By an elementary combinatorial function (ex. function) we mean any function which can be given a definition of the form

where E1(x1, …, xn), …, Ek(x1, …, xn) is an enumeration of all consistent elementary conditions in x1, …, xn, and all the numbers d1, …, dk are among 1, …, n.

Examples. (1) The identity function is the only 1-ary e.c. function.

(2) A useful 3-ary e.c. function will be called J. The definition is

Let α be an admissible ordinal and let L be the first order language with equality and a single binary relation ≤. The elementary theory of the α-degrees is the set of all sentences of L which are true in the universe of the α-degrees when ≤ is interpreted as the partial ordering of the α-degrees. Lachlan [6] showed that the elementary theory of the ω-degrees is nonaxiomatizable by proving that any countable distributive lattice with greatest and least members can be imbedded as an initial segment of the degrees of unsolvability. This paper deals with the extension of these results to α-recursion theory for an arbitrary countable admissible α > ω. Given α, we construct a set A with α-degree a such that every countable distributive lattice with greatest and least member is order isomorphic to a segment of α-degrees {d ∣ a ≤αd≤αb} for some α-degree b. As in [6] this implies that the elementary theory of the α-degrees is nonaxiomatizable and hence undecidable.

A is constructed in §2. A is a set of integers which is generic with respect to a suitable notion of forcing. Additional applications of such sets are summarized at the end of the section. In §3 we define the notion of a tree and construct a particular tree T0 which is weakly α-recursive in A. Using T0 we can apply the techniques of [6] and [2] to α-recursion theory. In §4 we reduce our main results to three technical lemmas concerning systems of trees. These lemmas are proved in §5.

In this paper, Cohen's forcing technique is applied to some problems in model theory. Forcing has been used as a model-theoretic technique by several people, in particular, by A. Robinson in a series of papers [1], [10], [11]. Here forcing will be used to expand a family of structures in such a way that weak second-order embeddings are preserved. The forcing situation resembles that in Solovay's proof that for any theorem φ of GB (Godel-Bernays set theory with a strong form of the axiom of choice), if φ does not mention classes, then it is already a theorem of ZFC. (See [3, p. 105] and [2, p. 77].)

The first application of forcing here is to the problem (posed by Keisler) of when is it possible to add a Skolem function to a pair of structures, one of which is an elementary substructure of the other, in such a way that the elementary embedding is preserved.

It is not always possible to find such a Skolem function. Payne [9] found an example involving countable structures with uncountably many relations. The author [4], [6] found an example involving uncountable structures with only two relations. The problem remains open in case the structures are required both to be countable and to have countable type. Forcing is used to obtain a positive result under some special conditions.

Nonstandard analysis was developed in [1] within a logic which has a language with finite types. In [2] and [3] the logic is first order and the language is that of set theory. The set theoretical approach can be described in the following setting.

Let be a relational structure (A, ∈) where A is a nonempty set and ∈ is a restriction of the elementhood relation of set theory.

Let Ext be the wf (∀x)[(∃w)[w ∈ x] → [(∀y)(∀z) [z ∈ x ↔ z ∈ y] → x = y]]. Call a fragment of set theory if ⊧ Ext. By forming a nontrivial ultrapower of one obtains a structure which, after canonically embedding in , becomes a proper elementary extension of .

Let j embed canonically in . Let be the substructure (B′, ∈′) of where B′ is the ∈′-closure of j(A) in B. That is, B′ is the smallest subset of B containing j(A) such that if b ∈ B, b′ ∈ B′ and ⊧ b ∈ b′ then b ∈ B′.

Tag systems were defined by Post [9], [10] and have been studied by a number of researchers including Minsky [7], Maslov [6] and Aanderaa and Belsnes [1]. In their recent paper Aanderaa and Belsnes demonstrated that every r.e. many-one degree (exclusive of the degree of the empty set) is represented by the general halting problem for tag systems, that is, by the family of halting problems ranging over all tag systems. Their result depends upon an informal proof of this property for Turing machines but may be seen to be correct in light of a formal proof due to Overbeek [8]. Our aim is to extend their results to the general word problem for these systems. Specifically, we shall present an effective method which, when applied to an arbitrary r.e. set S, where S is neither empty nor the set of all natural numbers, produces a tag system R′ whose word and halting problems are both of the same many-one degree as the decision problem for S. The proof is realized by first constructing, from the description of an arbitrary Turing machine M, which machine has at least one mortal and one immortal configuration, a 5-register machine R, whose word and halting problems are both of the same many-one degree as the halting problem for M. From R we then construct the desired tag system R′. This construction combined with Overbeek's [8] shows that every r.e. many-one degree (exclusive of the degrees of the empty set and the set of all natural numbers) is represented by the general word and halting problems for tag systems. Moreover our results are seen to be best possible with regard to degrees of unsolvability in that it is not the case that every nonrecursive r.e. one-one degree is represented by either of the general decision problems for tag systems which are considered here. These results were first shown in the author's thesis [3] and were announced in [4], They form part of an extensive study into the many-one equivalence of general decision problems. An overview of the initial findings of this research project may be found in [5].

Definition 1. For a set S and a cardinal κ,

In particular, 2ω denotes the power set of the natural numbers and not the cardinal 2ℵ0. We regard 2ω as a topological space with the usual product topology.

Definition 2. A set S ⊆ 2ω is Ramsey if there is an M ∈ [ω]ω such that either [M]ω ⊆ S or else [M]ω ⊆ 2ω − S.

Erdös and Rado [3, Example 1, p. 434] showed that not every S ⊆ 2ω is Ramsey. In view of the nonconstructive character of the counterexample, one might expect (as Dana Scott has suggested) that all sufficiently definable sets are Ramsey. In fact, our main result (Theorem 2) is that all Borei sets are Ramsey. Soare [10] has applied this result to some problems in recursion theory.

The first positive result on Scott's problem was Ramsey's theorem [8, Theorem A]. The next advance was Nash-Williams' generalization of Ramsey's theorem (Corollary 2), which can be interpreted as saying: If S1 and S2 are disjoint open subsets of 2ω, there is an M ∈ [ω]ω such that either [M]ω ⋂ S1 = ∅ or [M]ω ∩ S2 = ⊆. (This is halfway between “clopen sets are Ramsey” and “open sets are Ramsey.”) Then Galvin [4] stated a generalization of Nash-Williams' theorem (Corollary 1) which says, in effect, that open sets are Ramsey; this was discovered independently by Andrzej Ehrenfeucht, Paul Cohen, and probably many others, but no proof has been published.

The purpose of this paper is to give an axiom system for quantum logic. Here quantum logic is considered to have the structure of an orthomodular lattice. Some authors assume that it has the structure of an orthomodular poset.

In finding this axiom system the implication algebra given in Finch [1] has been very useful. Finch shows there that this algebra can be produced from an orthomodular lattice and vice versa.

Definition. An orthocomplementation N on a poset (partially ordered set) whose partial ordering is denoted by ≤ and which has least and greatest elements 0 and 1 is a unary operation satisfying the following:

(1) the greatest lower bound of a and Na exists and is 0,

(2) a ≤ b implies Nb ≤ Na,

(3) NNa = a.

Definition. An orthomodular lattice is a lattice with meet ∧, join ∨, least and greatest elements 0 and 1 and an orthocomplementation N satisfying

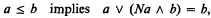
where a ≤ b means a ∧ b = a, as usual.

Definition. A Finch implication algebra is a poset with a partial ordering ≤, least and greatest elements 0 and 1 which is orthocomplemented by N. In addition, it has a binary operation → satisfying the following:

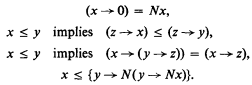
An orthomodular lattice gives a Finch implication algebra by defining → by

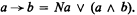
A Finch implication algebra can be changed into an orthomodular lattice by defining the meet ∧ and join ∨ by

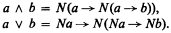
The orthocomplementation is unchanged in both cases.

This paper investigates the problem of extending the recursion theoretic construction of a minimal degree to the Kripke [2]-Platek [5] recursion theory on the ordinals less than an admissible ordinal α, a theory derived from the Takeuti [11] notion of a recursive function on the ordinal numbers. As noted in Sacks [7] when one generalizes the recursion theoretic definition of relative recursiveness to α-recursion theory for α > ω the two usual definitions give rise to two different notions of reducibility. We will show that whenever α is either a countable admissible or a regular cardinal of the constructible universe there is a subset of α whose degree is minimal for both notions of reducibility. The result is an excellent example of a theorem of ordinary recursion theory obtainable via two different constructions, one of which generalizes, the other of which does not. The construction which cannot be lifted to α-recursion theory is that of Spector [10]. We sketch the reasons for this in §3.

In [CLg. II, §15B6], the problem of representing equality in the system by means of an ob Q is discussed; it is shown there that if Q is taken to be a canonical atom of degree 2 and if the axiom scheme

is postulated, then it follows by Rule Eq that

and, if no other properties are postulated for Q, then the converse of (1), Q-consistency, also holds. However, it is also desirable to have, in addition, the property

at least for some obs Z, and the statement is made in [CLg. II, §15B6] that no known way of incorporating this principle existed (at the time this statement was written) in such a way that there was a proof of Q-consistency. In this paper it is shown that if Z is restricted to be a basic canob of degree 1, i.e., if Z is restricted to be a predicate of one argument, then a system in which (2) is postulated can be proved Q-consistent.

The notations and conventions of [CLg. II] especially §15B, will be used throughout the paper.

A recursively enumerable (r.e.) set is mitotic if it is the disjoint union of two r.e. sets both of the same degree of unsolvability. A. H. Lachlan has shown in [3] that there exists a nonmitotic r.e. set. In this paper we make an initial investigation into the class of mitotic sets.

The following results are proved, (i) An r.e. set is mitotic if and only if it is auto-reducible, (ii) There is a nonmitotic r.e. set of degree 0′, (iii) If d is an arbitrary non-recursive r.e. degree then there exists a nonmitotic r.e. set of degree ≤d. (iv) There exists a maximal set which is mitotic and a maximal set which is nonmitotic.

Albert R. Meyer had independently proved (ii) and (iii) for nonautoreducible sets before (i) was known.

The partial order structure of degrees of unsolvability represented by continuous type-2 functional is a proper extension of the partial order structure of type-1 degrees.

That elementary number theory is consistent and can be given a metamathematical consistency proof has been well known since Gentzen's 1936 paper, and a number of different proofs of this result have since been offered. What is presented here is essentially a simplified and generalized version of the proof given by Ackermann in 1940 [1]; but the proof given here applies to systems formalized in standard quantification theory rather than in Hilbert's ε-calculus, and is based upon the analysis of quantificational reasoning given by Herbrand's Fundamental Theorem. Dreben and Denton sketch such a proof in [2], but at a crucial point they follow Ackermann in tying the strategy of their proof too closely to the standard model. This makes the proof more complex than it need be and restricts its application to systems with induction on the standard well-ordering. The present proof is both simpler and more general in that it applies to systems ZR of number theory with induction on arbitrary recursive well-orderings R. This generalization was first obtained by Tait in [11] using functionals of lowest type. Some technical devices employed below are similar to ones used by Tait, but while the proof-theoretic methods employed here are naturally characterizable in terms of functionals of lowest type the present proof avoids the introduction of such functionals into the languages studied.

J. D. Monk has shown that for first order languages with finitely many variables there is no finite set of schema which axiomatizes the universally valid formulas. There are such finite sets of schema which axiomatize the formulas valid in all structures of some fixed finite size.

In this paper we develop certain methods of proof in Quine's set theory NF which have no counterparts elsewhere. These ideas were first used by Specker [5] in his disproof of the Axiom of Choice in NF. They depend on the properties of two related operations, T(n) on cardinal numbers and U(α) on ordinal numbers, which are defined by the equations

for each set x and well ordering R. (Here and below we use Rosser's notation [3].) The definitions insure that the formulas T(x) = y and U(x) = y are stratified when y is assigned a type one higher than x. The importance of T and U stems from the following facts: (i) each of T and U is a 1-1, order preserving operation from its domain onto a proper initial section of its domain; (ii) Tand U commute with most of the standard operations on cardinal and ordinal numbers.

These basic facts are discussed in §1. In §2 we prove in NF that the exponential function 2n is not 1-1. Indeed, there exist cardinal numbers m and n which satisfy

In §3 we prove the following technical result, which has many important applications. Suppose f is an increasing function from an initial segment S of the set NO of ordinal numbers into NO and that f commutes with U.

It is well known that the hypothesis that all real numbers are constructible in the sense of Gödel [1] implies the existence of a Σ21 well-ordering of the Baire space [1, p. 67]. We are concerned with the converse to this theorem. From the assumption of the existence of a Σ21 well-ordering with total domain, we derive various consequences which in the presence of a nonconstructible real seem highly pathological. However, while several of these consequences are obviously absurd, none have as yet been disproven. Indeed some of the stranger consistency proofs of Jensen seem to indicate that there is a possibility that they may be consistent. I am referring to such results as existence of a model for ZF set theory in which the degrees of constructibility form a sequence of type ω + 1 with the (ω + 1)st degree being the only one which contains a nonconstructible real, and that degree being the degree of a Δ31 nonconstructible real.

In what follows we shall use the small Greek letters α, β, γ to range over the Baire space NN where N is the set of natural numbers. We assume that the reader is familiar with the use of trees to encode closed subsets of this space. The class Σ21 is the collection of all those subsets of the Baire space which can be defined by a formula which is Σ21 in a constructible parameter. Correspondingly Π21 will be taken to mean Π11 in a constructible parameter. The proof of the first lemma is left as an exercise. It involves nothing more than coding perfect sets by trees and then counting quantifiers.

An important goal of complexity theory, as we see it, is to characterize those partial recursive functions and recursively enumerable sets having some given complexity properties, and to do so in terms which do not involve the notion of complexity.

As a contribution to this goal, we provide characterizations of the effectively speedable, speedable and levelable [2] sets in purely recursive theoretic terms. We introduce the notion of subcreativeness and show that every program for computing a partial recursive function f can be effectively speeded up on infinitely many integers if and only if the graph of f is subcreative.

In addition, in order to cast some light on the concepts of effectively speedable, speedable and levelable sets we show that all maximal sets are levelable (and hence speedable) but not effectively speedable and we exhibit a set which is not levelable in a very strong sense but yet is effectively speedable.

The purpose of this note is to give a short proof of a conjecture of Feiner that every countable Boolean algebra has an ordered basis that is a lexicographic sum of well-ordered sets over the ordered set η of all rational numbers. Actually, we prove a slightly more precise fact, which is formulated below as Theorem 3. An earlier proof of Feiner's conjecture was obtained by David Cossack (unpublished), using a different method.

Our proof will use the following property of Cantor's dyadic discontinuum D.