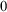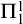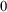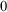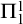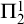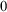1 Introduction
The general project of calibrating the complexity of mathematical theorems and constructions has two important and interrelated classes of measuring rods. One, embodied in what is now called reverse mathematics, is proof theoretic and attempts to determine what axioms are sufficient and even necessary to prove a given theorem. The other is recursion theoretic and attempts to determine how hard (in terms of computational complexity) it is to construct a desired object or how complicated must an object be to satisfy given specifications. Each approach has its standard yardsticks of complexity. For reverse mathematics these are axiom systems in second order arithmetic. For the computational approach they are ones measured by specific constructions. Most prominently, they are calibrated in terms of the Turing jump and its iterates and generalizations. (Standard texts are [Reference Hirschfeldt, Chong, Feng, Slaman, Woodin and Yang12, Reference Simpson28] which emphasize the first and second approaches, respectively.)
The early decades of this subject were marked by a large variety of results characterizing a wide array of theorems and constructions as being one of five or so specific levels of complexity. (These are Simpson’s “big five” axioms systems and the corresponding recursion theoretic construction principles.) They begin with RCA
![]() $_{0}$
which is the standard weak base theory for reverse mathematics. It includes the usual simple first order axioms about
$_{0}$
which is the standard weak base theory for reverse mathematics. It includes the usual simple first order axioms about
![]() $+,\times ,\leq ,\in ,0,1$
and induction for sets X as a free variable. The defining additional axiom scheme is
$+,\times ,\leq ,\in ,0,1$
and induction for sets X as a free variable. The defining additional axiom scheme is
![]() $\Delta _{1}^{0}$
-CA, comprehension for sets defined by both
$\Delta _{1}^{0}$
-CA, comprehension for sets defined by both
![]() $ \Sigma _{1}^{0}$
and
$ \Sigma _{1}^{0}$
and
![]() $\Pi _{1}^{0}$
formulas. This system corresponds to recursive constructions. We assume that it is included in every theory we consider. (For formal definitions and detailed information on all the systems see [Reference Simpson28].) In more recent decades, there has been a proliferation of results placing theorems and constructions outside the big five. Sometimes inserted linearly and sometimes with incomparabilities. They are now collectively often called the “zoo” of reverse mathematics. (For pictures, see https://rmzoo.math.uconn.edu/diagrams/.) The bulk of these interpolations have been at the lower end of these hierarchies. (Technically, this means below ACA
$\Pi _{1}^{0}$
formulas. This system corresponds to recursive constructions. We assume that it is included in every theory we consider. (For formal definitions and detailed information on all the systems see [Reference Simpson28].) In more recent decades, there has been a proliferation of results placing theorems and constructions outside the big five. Sometimes inserted linearly and sometimes with incomparabilities. They are now collectively often called the “zoo” of reverse mathematics. (For pictures, see https://rmzoo.math.uconn.edu/diagrams/.) The bulk of these interpolations have been at the lower end of these hierarchies. (Technically, this means below ACA
![]() $_{0}$
, the proof theoretic system whose defining axiom scheme is comprehension for arithmetic formulas. The recursion theoretic analog is the class of constructions which can be done effectively in finitely many iterations of the Turing jump.)
$_{0}$
, the proof theoretic system whose defining axiom scheme is comprehension for arithmetic formulas. The recursion theoretic analog is the class of constructions which can be done effectively in finitely many iterations of the Turing jump.)
The next systems of reverse mathematics are ATR
![]() $_{0}$
and
$_{0}$
and
![]() $\Pi _{1}^{1}$
-CA
$\Pi _{1}^{1}$
-CA
![]() $ _{0}$
which are defined, respectively, by transfinite iterations of arithmetic comprehension and comprehension for formulas with one second order quantifier followed by an arithmetic formula. Recursion theoretically these roughly correspond to transfinite effective iterations of the Turing jump (hyperarithmetic sets) and Kleene’s hyperjump. A fair number of mathematical theorems and constructions have turned up at precisely these levels but very few between them or above them.
$ _{0}$
which are defined, respectively, by transfinite iterations of arithmetic comprehension and comprehension for formulas with one second order quantifier followed by an arithmetic formula. Recursion theoretically these roughly correspond to transfinite effective iterations of the Turing jump (hyperarithmetic sets) and Kleene’s hyperjump. A fair number of mathematical theorems and constructions have turned up at precisely these levels but very few between them or above them.
As in Barnes, Goh, and Shore [Reference Barnes, Goh and Shore1] (hereafter BGS) which led to this work, our concerns here are with a particularly unusual area of these hierarchies lying recursion theoretically above each fixed bounded countable iteration of the Turing jump but proof theoretically below the system ATR
![]() $_{0}$
. It has a precise recursion theoretic definition (Definition 2.9) but, as the definition relies on using only the standard model of arithmetic and only true well orderings, it lacks a good proof theoretic definition (at least in first order logic). (See [Reference Van Wesep31, Theorem 2.2.2] and also [Reference Montalbán20, remarks after Definition 1.1].) Theorems and theories at this level are called ones of hyperarithmetic analysis (so THAs).
$_{0}$
. It has a precise recursion theoretic definition (Definition 2.9) but, as the definition relies on using only the standard model of arithmetic and only true well orderings, it lacks a good proof theoretic definition (at least in first order logic). (See [Reference Van Wesep31, Theorem 2.2.2] and also [Reference Montalbán20, remarks after Definition 1.1].) Theorems and theories at this level are called ones of hyperarithmetic analysis (so THAs).
There are quite a number of logical theories including ones about choice (
![]() $ \Sigma _{1}^{1}$
-AC
$ \Sigma _{1}^{1}$
-AC
![]() $_{0}$
) and comprehension (
$_{0}$
) and comprehension (
![]() $\Delta _{1}^{1}$
-CA
$\Delta _{1}^{1}$
-CA
![]() $_{0}$
) that fall in this realm. Many were well studied in the 60s and 70s both before and after the introduction of the program of reverse mathematics [Reference Friedman6, Reference Friedman7]. Until BGS, however, there was only one mathematical but not logical example, i.e., one not mentioning classes of first order formulas or their syntactic complexity. It was a result (INDEC) about indecomposability of linear orderings in Jullien’s [Reference Jullien17] thesis (see [Reference Rosenstein25, Lemma 10.3]). It was shown to be a THA by Montalbán [Reference Montalbán20] who investigated its place among the older systems as well as several other logical ones using variations of Steel forcing. In 2008 he included
$_{0}$
) that fall in this realm. Many were well studied in the 60s and 70s both before and after the introduction of the program of reverse mathematics [Reference Friedman6, Reference Friedman7]. Until BGS, however, there was only one mathematical but not logical example, i.e., one not mentioning classes of first order formulas or their syntactic complexity. It was a result (INDEC) about indecomposability of linear orderings in Jullien’s [Reference Jullien17] thesis (see [Reference Rosenstein25, Lemma 10.3]). It was shown to be a THA by Montalbán [Reference Montalbán20] who investigated its place among the older systems as well as several other logical ones using variations of Steel forcing. In 2008 he included
![]() $ \Pi _{1}^{1}$
-Separation and new forcing variations. More analysis was provided by Neeman [Reference Neeman23, Reference Neeman24].
$ \Pi _{1}^{1}$
-Separation and new forcing variations. More analysis was provided by Neeman [Reference Neeman23, Reference Neeman24].
This situation provoked the question as to whether there are other results from the mathematical literature that are THAs. The issue was raised explicitly in Montalbán’s “Open Questions in Reverse Mathematics” [Reference Montalbán22, Q30]. It was answered by BGS who provide a host of such examples and study the relations among them and to previously known systems. (See also [Reference Goh9].) These were all variations and generalizations of a classical theorem of [Reference Halin10] in graph theory (Definition 2.5). (See also [Reference Halin11] and, for a contemporary treatment and references, [Reference Diestel5, Chapter 8].)
This paper grew out of a proof of what we would call a reduction (actually providing an equivalence) between two of these principles in Bowler, Carmesin, and Pott [Reference Bowler, Carmesin and Pott2] (hereafter BCP). While BGS provide a number of such results in RCA
![]() $_{0}$
, the reduction in BCP did not seem to fit the mold. The proof sketch provided there appeared to be elementary. However, a closer look showed that underneath it seemed to use methods that were themselves THAs and about as strong as the principles being proven equivalent. Our expectation was that these methods, like most of the ones studied in BGS, would also prove to be THAs. That turned out not to be the case. Rather, the graph theoretic principle (Definition 3.5) that they used (that allowed one to restrict attention to locally finite graphs) implied (over ACA
$_{0}$
, the reduction in BCP did not seem to fit the mold. The proof sketch provided there appeared to be elementary. However, a closer look showed that underneath it seemed to use methods that were themselves THAs and about as strong as the principles being proven equivalent. Our expectation was that these methods, like most of the ones studied in BGS, would also prove to be THAs. That turned out not to be the case. Rather, the graph theoretic principle (Definition 3.5) that they used (that allowed one to restrict attention to locally finite graphs) implied (over ACA
![]() $_{0}$
) some known THAs. The unusual aspect of the situation was that we could prove that it was not possible to show that they implied any known THA in RCA
$_{0}$
) some known THAs. The unusual aspect of the situation was that we could prove that it was not possible to show that they implied any known THA in RCA
![]() $_{0}$
. In particular they did not even imply ACA
$_{0}$
. In particular they did not even imply ACA
![]() $_{0}$
. We call such principles/theorems/theories almost theorems/theories of hyperarithmetic analysis (ATHAs; Definition 2.10).
$_{0}$
. We call such principles/theorems/theories almost theorems/theories of hyperarithmetic analysis (ATHAs; Definition 2.10).
Indeed, the one that was used in BCP and several variants are very weak over ACA
![]() $_{0}$
. They are
$_{0}$
. They are
![]() $\Pi _{1}^{1}$
, r-
$\Pi _{1}^{1}$
, r-
![]() $\Pi _{2}^{1}$
(Definitions 4.8–4.10), and Tanaka (Definition 7.1) conservative over RCA
$\Pi _{2}^{1}$
(Definitions 4.8–4.10), and Tanaka (Definition 7.1) conservative over RCA
![]() $_{0}$
(and more). We extend all our conservation results to what seem to be new classes of formulas by allowing, in addition to the basic formulas in these classes, closure under conjunctions, disjunctions, first order quantifiers, and universal second order quantifiers (see Definitions 4.9, 4.10, and 7.1). These results also provide extended conservation results for many previously studied theories. In addition, given any countable model
$_{0}$
(and more). We extend all our conservation results to what seem to be new classes of formulas by allowing, in addition to the basic formulas in these classes, closure under conjunctions, disjunctions, first order quantifiers, and universal second order quantifiers (see Definitions 4.9, 4.10, and 7.1). These results also provide extended conservation results for many previously studied theories. In addition, given any countable model
![]() $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
![]() $_{0}$
and any countable collection of subtrees of the tree
$_{0}$
and any countable collection of subtrees of the tree
![]() $N^{<N}$
(of
$N^{<N}$
(of
![]() $ \mathcal {N}$
) (even ones which are not themselves sets in N) which have no branches in
$ \mathcal {N}$
) (even ones which are not themselves sets in N) which have no branches in
![]() $\mathcal {N}$
, we can construct an extension
$\mathcal {N}$
, we can construct an extension
![]() $\mathcal {N} ^{\prime }$
with the same first order part satisfying these principles which adds no branch to any of these subtrees. So, in particular, given any countable collection of subsets of N, one can avoid adding any of them not already in
$\mathcal {N} ^{\prime }$
with the same first order part satisfying these principles which adds no branch to any of these subtrees. So, in particular, given any countable collection of subsets of N, one can avoid adding any of them not already in
![]() $\mathcal {N}$
to the extension
$\mathcal {N}$
to the extension
![]() $\mathcal {N}^{\prime }$
. (An interesting example here is the collection of all subsets of N definable over
$\mathcal {N}^{\prime }$
. (An interesting example here is the collection of all subsets of N definable over
![]() $\mathcal {N}$
.) Moreover, one can construct such extensions
$\mathcal {N}$
.) Moreover, one can construct such extensions
![]() $\mathcal {N} _{0}$
and
$\mathcal {N} _{0}$
and
![]() $\mathcal {N}_{1}$
of
$\mathcal {N}_{1}$
of
![]() $\mathcal {N}$
so that the intersection of their second order parts is that part of
$\mathcal {N}$
so that the intersection of their second order parts is that part of
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
We also show that many simple variations of known THAs such as
![]() $\Sigma _{1}^{1}$
-AC are also ATHAs with all these weakness properties over RCA
$\Sigma _{1}^{1}$
-AC are also ATHAs with all these weakness properties over RCA
![]() $_{0}$
. We prove these results by showing that all the principles studied here can be made true by iterating forcings from a quite general class of forcings that can be implemented to guarantee the conservation and branch or set omitting properties just described. On the other hand, when combined with ACA
$_{0}$
. We prove these results by showing that all the principles studied here can be made true by iterating forcings from a quite general class of forcings that can be implemented to guarantee the conservation and branch or set omitting properties just described. On the other hand, when combined with ACA
![]() $_{0}$
each of these principles is equivalent to an already studied one known to be a THA. We then point out various known separation results for the old principles that also distinguishing among some of these new theories over RCA
$_{0}$
each of these principles is equivalent to an already studied one known to be a THA. We then point out various known separation results for the old principles that also distinguishing among some of these new theories over RCA
![]() $_{0}$
.
$_{0}$
.
Finally, we extend our methods to prove similar results for hierarchies of variations of choice principles that are much stronger than
![]() $\Sigma _{1}^{1}$
-AC and so well beyond THAs. At the end of these hierarchies, we provide principles that have all the same conservation and branch/set omitting properties over RCA
$\Sigma _{1}^{1}$
-AC and so well beyond THAs. At the end of these hierarchies, we provide principles that have all the same conservation and branch/set omitting properties over RCA
![]() $_{0}$
but when combined with ACA
$_{0}$
but when combined with ACA
![]() $_{0}$
are strictly stronger than full second order arithmetic. We also discuss another type of conservation result for sentences of the form
$_{0}$
are strictly stronger than full second order arithmetic. We also discuss another type of conservation result for sentences of the form
![]() $\forall X\exists !Y\Phi (X,Y)$
conjectured by Tanaka for WKL
$\forall X\exists !Y\Phi (X,Y)$
conjectured by Tanaka for WKL
![]() $_{0}$
and proved for it in Simpson, Tanaka, and Yamazaki [Reference Simpson, Tanaka and Yamazaki29] (hereafter STY) as well as strengthenings to include larger classes of sentences (see Definition 7.1).
$_{0}$
and proved for it in Simpson, Tanaka, and Yamazaki [Reference Simpson, Tanaka and Yamazaki29] (hereafter STY) as well as strengthenings to include larger classes of sentences (see Definition 7.1).
Thus, we view this paper not only as introducing a new interesting realm of the reverse mathematics/recursion theoretic universe but as also answering the question raised in [Reference Montalbán22, 6.1.1] immediately after the one about the existence of mathematical THA. Attributing the question to Hirschfeldt, Montalbán points out that there are very few examples where natural equivalences are known to hold over strong theories but not over RCA
![]() $ _{0}$
particularly if one excludes the cases where the only additional axioms needed are forms of induction. Hirschfeldt asked for more. We would say that this paper provides a whole array of pairs of principles which are equivalent over ACA
$ _{0}$
particularly if one excludes the cases where the only additional axioms needed are forms of induction. Hirschfeldt asked for more. We would say that this paper provides a whole array of pairs of principles which are equivalent over ACA
![]() $_{0}$
but not over RCA
$_{0}$
but not over RCA
![]() $_{0}$
and so evidence that in some settings it would make sense to take ACA
$_{0}$
and so evidence that in some settings it would make sense to take ACA
![]() $_{0}$
as the base theory for reverse mathematical investigations rather than RCA
$_{0}$
as the base theory for reverse mathematical investigations rather than RCA
![]() $_{0}$
.
$_{0}$
.
1.1 Outline of the paper
We provide the needed basic graph theoretic notions and principles in Section 2. The next section (Section 3) presents the principles used in BCP as mentioned above as well as some related graph theoretic principles and analyzes their strength over ACA
![]() $_{0}$
. In particular, we show that, over ACA
$_{0}$
. In particular, we show that, over ACA
![]() $_{0}$
, each of them implies some known THAs. In Section 4, we define a large class of forcings that include many well-known ones such as Cohen, Laver, Mathias, Sacks, and Silver forcing and many variations. We then show that generic extensions by any such forcing have all the preservation properties suggested above. Thus any principle that can be made true by iterating such forcings have the conservation and other weakness properties already mentioned. In particular, if the principles are
$_{0}$
, each of them implies some known THAs. In Section 4, we define a large class of forcings that include many well-known ones such as Cohen, Laver, Mathias, Sacks, and Silver forcing and many variations. We then show that generic extensions by any such forcing have all the preservation properties suggested above. Thus any principle that can be made true by iterating such forcings have the conservation and other weakness properties already mentioned. In particular, if the principles are
![]() $\Pi _{2}^{1}$
(see Definition 4.7), and for any instance of the principle there is a forcing in our class that adds a solution, a standard
$\Pi _{2}^{1}$
(see Definition 4.7), and for any instance of the principle there is a forcing in our class that adds a solution, a standard
![]() $\omega $
-length iteration of such forcings guarantees the truth of the principle in the limit model. This supplies all the conservation results for such
$\omega $
-length iteration of such forcings guarantees the truth of the principle in the limit model. This supplies all the conservation results for such
![]() $\Pi _{2}^{1}$
principles and includes many previously known theorems as well as strengthenings of conservation results to larger classes of formulas.
$\Pi _{2}^{1}$
principles and includes many previously known theorems as well as strengthenings of conservation results to larger classes of formulas.
However, the ATHAs in which we are mainly interested are not
![]() $\Pi _{2}^{1}$
principles so some additional twists are needed in addition to supplying the appropriate forcing notions. We analyze the argument of BCP mentioned above as the first (and in many ways the most interesting) of our examples. The definition of the forcing notion and the proof that it supplies solutions to the relevant principles are in Theorem 5.1. To get an iteration that solves all instances of the principle and so provides the desired conservation and weakness properties, we use one of length
$\Pi _{2}^{1}$
principles so some additional twists are needed in addition to supplying the appropriate forcing notions. We analyze the argument of BCP mentioned above as the first (and in many ways the most interesting) of our examples. The definition of the forcing notion and the proof that it supplies solutions to the relevant principles are in Theorem 5.1. To get an iteration that solves all instances of the principle and so provides the desired conservation and weakness properties, we use one of length
![]() $\omega _{1}$
(Theorem 5.2). We then turn our attention to various weaker versions or instances of
$\omega _{1}$
(Theorem 5.2). We then turn our attention to various weaker versions or instances of
![]() $\Sigma _{1}^{1}$
-AC for our next source of ATHAs. Some of these (mathematical as well as logical) appeared naturally in BGS. Others are variations of well-studied classes of choice principles weaker than
$\Sigma _{1}^{1}$
-AC for our next source of ATHAs. Some of these (mathematical as well as logical) appeared naturally in BGS. Others are variations of well-studied classes of choice principles weaker than
![]() $\Sigma _{1}^{1}$
-AC. They are all weak over RCA
$\Sigma _{1}^{1}$
-AC. They are all weak over RCA
![]() $_{0}$
but equivalent to one of the known THAs over ACA
$_{0}$
but equivalent to one of the known THAs over ACA
![]() $_{0}.$
Examples here include unique and finite choice versions of
$_{0}.$
Examples here include unique and finite choice versions of
![]() $\Sigma _{1}^{1}$
-AC. (The former is generally known as weak
$\Sigma _{1}^{1}$
-AC. (The former is generally known as weak
![]() $\Sigma _{1}^{1}$
-AC. The latter is a consequence of the Halin type theorems studied and proven to be THAs in BGS and placed with respect to other studied versions of
$\Sigma _{1}^{1}$
-AC. The latter is a consequence of the Halin type theorems studied and proven to be THAs in BGS and placed with respect to other studied versions of
![]() $\Sigma _{1}^{1}$
-AC in [Reference Goh9].)
$\Sigma _{1}^{1}$
-AC in [Reference Goh9].)
In Section 6 we move beyond
![]() $\Sigma _{1}^{1}$
-AC and study weak version of higher order axioms of choice. The appropriate forcing notions in our class are not hard to come by. As the principles are of arbitrary syntactic complexity, it is not immediate, for example, that adding something that may look like a solution during the construction will actually be a solution at the end of even an
$\Sigma _{1}^{1}$
-AC and study weak version of higher order axioms of choice. The appropriate forcing notions in our class are not hard to come by. As the principles are of arbitrary syntactic complexity, it is not immediate, for example, that adding something that may look like a solution during the construction will actually be a solution at the end of even an
![]() $\omega _{1}$
length iteration. In the strongest case, we modify what it means to provide solutions (Theorem 6.1). We then use the fact that there is a closed unbounded set of ordinals
$\omega _{1}$
length iteration. In the strongest case, we modify what it means to provide solutions (Theorem 6.1). We then use the fact that there is a closed unbounded set of ordinals
![]() $\alpha $
such that the models
$\alpha $
such that the models
![]() $\mathcal {N}_{\alpha }$
are elementary submodels (in the second order language) of our limit model
$\mathcal {N}_{\alpha }$
are elementary submodels (in the second order language) of our limit model
![]() $\mathcal {N}_{\omega _{1}}$
to show that it has the desired properties (Theorem 6.2). A short argument (Theorem 6.3) shows that the whole hierarchies of weak principles are equivalent to the standard choice axioms (
$\mathcal {N}_{\omega _{1}}$
to show that it has the desired properties (Theorem 6.2). A short argument (Theorem 6.3) shows that the whole hierarchies of weak principles are equivalent to the standard choice axioms (
![]() $\Sigma _{n+1}^{1}$
-AC) over ACA
$\Sigma _{n+1}^{1}$
-AC) over ACA
![]() $_{0}$
. At the end, we have two principles with all our conservation and preservation properties which over ACA
$_{0}$
. At the end, we have two principles with all our conservation and preservation properties which over ACA
![]() $_{0}$
are equivalent to the union of all the
$_{0}$
are equivalent to the union of all the
![]() $\Sigma _{n+1}^{1}$
-AC and so strictly stronger than full second order arithmetic.
$\Sigma _{n+1}^{1}$
-AC and so strictly stronger than full second order arithmetic.
The last section is devoted first to a description of about 10-year-old but unpublished work by Tanaka, Montalbán, and primarily Yamazaki getting some of our conservation results for what they call the collection axioms
![]() $ \Pi _{n}^{1}$
and
$ \Pi _{n}^{1}$
and
![]() $\Pi _{\infty }^{1}$
(in our terminology
$\Pi _{\infty }^{1}$
(in our terminology
![]() $\Sigma _{n+1}^{1} $
-AC
$\Sigma _{n+1}^{1} $
-AC
![]() $^{-}$
and
$^{-}$
and
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
). They also extend even earlier work on WKL
$^{-}$
). They also extend even earlier work on WKL
![]() $_{0}$
in STY to get Tanaka conservation (Definition 7.1) for the collection axioms and a couple of other principles. Motivated by this work, we have proven the same and stronger conservation results for all the ATHA principles we consider in this paper for which we use forcing constructions to show that they are very weak over RCA
$_{0}$
in STY to get Tanaka conservation (Definition 7.1) for the collection axioms and a couple of other principles. Motivated by this work, we have proven the same and stronger conservation results for all the ATHA principles we consider in this paper for which we use forcing constructions to show that they are very weak over RCA
![]() $_{0}$
and, in particular, do not imply ACA
$_{0}$
and, in particular, do not imply ACA
![]() $_{0}$
. The basic conservation result (over RCA
$_{0}$
. The basic conservation result (over RCA
![]() $_{0})$
they prove is for sentences of the form
$_{0})$
they prove is for sentences of the form
![]() $\forall X\exists !Y\Phi (X,Y)$
with
$\forall X\exists !Y\Phi (X,Y)$
with
![]() $\Phi $
arithmetic. We get the same results for all of our principles and most of theirs by what seem to be much simpler constructions. In addition, we extend the class of sentences covered by our methods analogously to the extensions made for
$\Phi $
arithmetic. We get the same results for all of our principles and most of theirs by what seem to be much simpler constructions. In addition, we extend the class of sentences covered by our methods analogously to the extensions made for
![]() $\Pi _{1}^{1}$
and r-
$\Pi _{1}^{1}$
and r-
![]() $\Pi _{2}^{1}$
in previous sections. While handling the basic Tanaka conservativity requires some additional notions, the extensions are dealt with as in the
$\Pi _{2}^{1}$
in previous sections. While handling the basic Tanaka conservativity requires some additional notions, the extensions are dealt with as in the
![]() $\Pi _{1}^{1}$
and r-
$\Pi _{1}^{1}$
and r-
![]() $\Pi _{2}^{1}$
conservation results mentioned above.
$\Pi _{2}^{1}$
conservation results mentioned above.
2 Basic notions
Formally, we are working in a model
![]() $\mathcal {N}=(N,S(\mathcal {N}),+,\times , \leq ,\in ,0,1)$
of second order arithmetic. (The first order quantifiers range over N. The second order ones over
$\mathcal {N}=(N,S(\mathcal {N}),+,\times , \leq ,\in ,0,1)$
of second order arithmetic. (The first order quantifiers range over N. The second order ones over
![]() $S(\mathcal {N})$
which is a collection of subset of N.) We generally abbreviate the structures as
$S(\mathcal {N})$
which is a collection of subset of N.) We generally abbreviate the structures as
![]() $ \mathcal {N}=(N,S(\mathcal {N}))$
. We are interested in ones which are models of RCA
$ \mathcal {N}=(N,S(\mathcal {N}))$
. We are interested in ones which are models of RCA
![]() $_{0}$
. When we define semantics or forcing we expand the formal language to include constants for each element of N and
$_{0}$
. When we define semantics or forcing we expand the formal language to include constants for each element of N and
![]() $S(\mathcal {N})$
and possibly some recursive (
$S(\mathcal {N})$
and possibly some recursive (
![]() $\Delta _{1}^{0}$
) predicates. (See Remark 4.4.) Informally, one can think of N as the standard natural numbers
$\Delta _{1}^{0}$
) predicates. (See Remark 4.4.) Informally, one can think of N as the standard natural numbers
![]() $\mathbb {N}$
with the usual operations and relations (and constants for every n and some class of subsets of
$\mathbb {N}$
with the usual operations and relations (and constants for every n and some class of subsets of
![]() $\mathbb {N}$
as well, perhaps, the predicate representing the universal Turing machine as in Remark 4.4). We use standard recursive codings of finite sequences, functions, relations, and structures to represent all such objects as elements of N or
$\mathbb {N}$
as well, perhaps, the predicate representing the universal Turing machine as in Remark 4.4). We use standard recursive codings of finite sequences, functions, relations, and structures to represent all such objects as elements of N or
![]() $S(\mathcal {N)}$
and abuse notation by saying that such objects are in N or
$S(\mathcal {N)}$
and abuse notation by saying that such objects are in N or
![]() $S(\mathcal {N)}$
, or even just by saying that they are in
$S(\mathcal {N)}$
, or even just by saying that they are in
![]() $\mathcal {N}$
, to mean that the corresponding codes are in
$\mathcal {N}$
, to mean that the corresponding codes are in
![]() $N$
or
$N$
or
![]() $S( \mathcal {N})$
. Unless otherwise specified, all sets and structures we consider are countable.
$S( \mathcal {N})$
. Unless otherwise specified, all sets and structures we consider are countable.
Definition 2.1. A graph H is a pair
![]() $\left \langle V,E\right \rangle $
consisting of a set V (of vertices) and a set E of unordered pairs
$\left \langle V,E\right \rangle $
consisting of a set V (of vertices) and a set E of unordered pairs
![]() $\{u,v\}$
with
$\{u,v\}$
with
![]() $u\neq v$
from V (called edges). These structures are also called undirected graphs (or here U-graphs). A structure H of the form
$u\neq v$
from V (called edges). These structures are also called undirected graphs (or here U-graphs). A structure H of the form
![]() $\left \langle V,E\right \rangle $
as above is a directed graph (or here D-graphs) if E consists of ordered pairs
$\left \langle V,E\right \rangle $
as above is a directed graph (or here D-graphs) if E consists of ordered pairs
![]() $\left \langle u,v\right \rangle $
of vertices with
$\left \langle u,v\right \rangle $
of vertices with
![]() $u\neq v$
. To handle both cases simultaneously, we often use X to stand for undirected (U) or directed (D). We then use
$u\neq v$
. To handle both cases simultaneously, we often use X to stand for undirected (U) or directed (D). We then use
![]() $(u,v)$
to stand for the appropriate kind of edge, i.e.,
$(u,v)$
to stand for the appropriate kind of edge, i.e.,
![]() $\{u,v\}$
or
$\{u,v\}$
or
![]() $\left \langle u.v\right \rangle $
. Any such H is locally finite if, for each
$\left \langle u.v\right \rangle $
. Any such H is locally finite if, for each
![]() $u\in V$
, the set
$u\in V$
, the set
![]() $\{v|(u,v)\in E\vee (v,u)\in E\}$
of neighbors of u is finite.
$\{v|(u,v)\in E\vee (v,u)\in E\}$
of neighbors of u is finite.
An X-subgraphof the X-graph H is an X-graph
![]() $ H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
such that
$ H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
such that
![]() $ V^{\prime }\subseteq V$
and
$ V^{\prime }\subseteq V$
and
![]() $E^{\prime }\subseteq E$
.
$E^{\prime }\subseteq E$
.
Definition 2.2. An X-ray in H is pair consisting of an X-subgraph
![]() $H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
and an isomorphism
$H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
and an isomorphism
![]() $f_{H^{\prime }}$
from N with edges
$f_{H^{\prime }}$
from N with edges
![]() $(n,n+1)$
for
$(n,n+1)$
for
![]() $n\in N$
to
$n\in N$
to
![]() $H^{\prime }$
. We also describe this situation by saying that H contains the X-ray
$H^{\prime }$
. We also describe this situation by saying that H contains the X-ray
![]() $\left \langle H^{\prime },f_{H^{\prime }}\right \rangle $
. We sometimes abuse notation by saying that the sequence
$\left \langle H^{\prime },f_{H^{\prime }}\right \rangle $
. We sometimes abuse notation by saying that the sequence
![]() $\left \langle f(n)\right \rangle $
of vertices is an X-ray in H.
$\left \langle f(n)\right \rangle $
of vertices is an X-ray in H.
H contains k many X-rays for
![]() $k\in N$
if there is a sequence
$k\in N$
if there is a sequence
![]() $\left \langle H_{i},f_{i}\right \rangle _{i<k}$
such that each
$\left \langle H_{i},f_{i}\right \rangle _{i<k}$
such that each
![]() $ \left \langle H_{i},f_{i}\right \rangle $
is an X-ray in H (with
$ \left \langle H_{i},f_{i}\right \rangle $
is an X-ray in H (with
![]() $ H_{i}=\left \langle V_{i},E_{i}\right \rangle $
).
$ H_{i}=\left \langle V_{i},E_{i}\right \rangle $
).
H contains k many disjoint (or vertex-disjoint) rays if the
![]() $V_{i}$
are pairwise disjoint. H contains k many edge-disjoint rays if the
$V_{i}$
are pairwise disjoint. H contains k many edge-disjoint rays if the
![]() $E_{i}$
are pairwise disjoint. We often use Y to stand for either vertex (V) or edge (E) as in the following definitions.
$E_{i}$
are pairwise disjoint. We often use Y to stand for either vertex (V) or edge (E) as in the following definitions.
An X-graph H contains arbitrarily many Y-disjoint X-rays if it contains k many such rays for every
![]() $k\in N$
.
$k\in N$
.
An X-graph H contains infinitely many Y-disjoint rays if there is an X-subgraph
![]() $H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
of H and a sequence
$H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
of H and a sequence
![]() $\left \langle H_{i},f_{i}\right \rangle _{i\in N}$
such that each
$\left \langle H_{i},f_{i}\right \rangle _{i\in N}$
such that each
![]() $\left \langle H_{i},f_{i}\right \rangle $
is an X-ray in H (with
$\left \langle H_{i},f_{i}\right \rangle $
is an X-ray in H (with
![]() $H_{i}=\left \langle V_{i},E_{i}\right \rangle $
) such that the
$H_{i}=\left \langle V_{i},E_{i}\right \rangle $
) such that the
![]() $V_{i}$
or
$V_{i}$
or
![]() $E_{i}$
, respectively for
$E_{i}$
, respectively for
![]() $Y=V,E$
, are pairwise disjoint and
$Y=V,E$
, are pairwise disjoint and
![]() $V^{\prime }=\cup V_{i}$
and
$V^{\prime }=\cup V_{i}$
and
![]() $ E^{\prime }=\cup E_{i}$
. (The requirement here that the set of rays
$ E^{\prime }=\cup E_{i}$
. (The requirement here that the set of rays
![]() $ \left \langle H_{i}\right \rangle _{i\in N}$
form or be contained in a subgraph is missing from the case of a finite sequence of rays
$ \left \langle H_{i}\right \rangle _{i\in N}$
form or be contained in a subgraph is missing from the case of a finite sequence of rays
![]() $\left \langle H_{i}\right \rangle _{i<k}$
above. The reason is that it is automatic in the finite case but not the infinite one. In the former, the unions
$\left \langle H_{i}\right \rangle _{i<k}$
above. The reason is that it is automatic in the finite case but not the infinite one. In the former, the unions
![]() $V^{\prime }$
and
$V^{\prime }$
and
![]() $E^{\prime }$
of the
$E^{\prime }$
of the
![]() $V_{i}$
and
$V_{i}$
and
![]() $E_{i}$
are always sets in the model as, e.g.,
$E_{i}$
are always sets in the model as, e.g.,
![]() $v\in V^{\prime }\Leftrightarrow (\exists i<k)(\left \langle i,v\right \rangle \in \left \langle H_{i}\right \rangle _{i<k})$
. If the index set, however, is N, then the quantifier is unbounded and the union may not exist in a model of RCA
$v\in V^{\prime }\Leftrightarrow (\exists i<k)(\left \langle i,v\right \rangle \in \left \langle H_{i}\right \rangle _{i<k})$
. If the index set, however, is N, then the quantifier is unbounded and the union may not exist in a model of RCA
![]() $_{0}$
. Of course, it always exists in models of ACA
$_{0}$
. Of course, it always exists in models of ACA
![]() $ _{0}$
.)
$ _{0}$
.)
Definition 2.3. An X-path P in an X-graph H is defined similarly to single rays except that the domain of f is a proper initial segment of
![]() $ \mathbb {N}$
instead of
$ \mathbb {N}$
instead of
![]() $\mathbb {N}$
itself. Thus they are finite sequences of distinct vertices with edges between successive vertices in the sequence. If
$\mathbb {N}$
itself. Thus they are finite sequences of distinct vertices with edges between successive vertices in the sequence. If
![]() $P=\left \langle x_{0},\ldots ,x_{n}\right \rangle $
is a path, we say it is a path of length n from
$P=\left \langle x_{0},\ldots ,x_{n}\right \rangle $
is a path, we say it is a path of length n from
![]() $x_{0}$
to
$x_{0}$
to
![]() $x_{n}$
.
$x_{n}$
.
Definition 2.4. A tree is a graph T with a designated element r called its root such that for each vertex
![]() $v\neq r$
there is a unique path from r to v. A branch in a tree T is a ray in T starting at its root. The set of all branches in T is denoted by
$v\neq r$
there is a unique path from r to v. A branch in a tree T is a ray in T starting at its root. The set of all branches in T is denoted by
![]() $[T]$
. Note, however, we are restricting ourselves to what would (in set theory) be called countable trees with all nodes of finite rank. Thus, we typically think of trees as subtrees of
$[T]$
. Note, however, we are restricting ourselves to what would (in set theory) be called countable trees with all nodes of finite rank. Thus, we typically think of trees as subtrees of
![]() $N^{<N}$
, i.e., the downward closed (under extension) sets of finite strings of numbers (as vertices) with an edge between
$N^{<N}$
, i.e., the downward closed (under extension) sets of finite strings of numbers (as vertices) with an edge between
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
if and only if they differ by one being an extension of the other by one element, e.g.,
$\tau $
if and only if they differ by one being an extension of the other by one element, e.g.,
![]() and with root
and with root
![]() $\emptyset $
. We call the longest
$\emptyset $
. We call the longest
![]() $\sigma $
which is comparable (under extension) with every element of such a tree its stem.
$\sigma $
which is comparable (under extension) with every element of such a tree its stem.
The starting point of the work in BGS and this paper is a theorem of Halin [Reference Halin10] that we call the infinite ray theorem as expressed in [Reference Diestel5, Theorem 8.2.5(i)].
Definition 2.5 (Halin’s theorem).
IRT, the infinite ray theorem,is the principle that every graph H which contains arbitrarily many disjoint rays contains infinitely many.
The versions of Halin’s theorem which we consider in this paper allow for H to be an undirected or a directed graph and for the disjointness requirement to be vertex or edge. They are labeled along the lines of BGS as IRT
![]() $_{XY}$
to indicate whether the graphs are undirected or directed (
$_{XY}$
to indicate whether the graphs are undirected or directed (
![]() $X=U$
or D) and whether the disjointness refers to the vertices or edges (
$X=U$
or D) and whether the disjointness refers to the vertices or edges (
![]() $Y=V$
or E) in the obvious way. We often state a theorem for all
$Y=V$
or E) in the obvious way. We often state a theorem for all
![]() $XY$
and then in the proof use “graph,” “edge,” and “disjoint” unmodified with the intention that the proof can be read for any of the four cases.
$XY$
and then in the proof use “graph,” “edge,” and “disjoint” unmodified with the intention that the proof can be read for any of the four cases.
Remark 2.6. We point out that unlike BGS (except in Remark 5.11) we do not consider the analogs of IRT for double rays (isomorphic to
![]() $ \mathbb {Z}$
rather than
$ \mathbb {Z}$
rather than
![]() $\mathbb {N}$
). Halin [Reference Halin11] proved the basic case here (UV) and BCP did the UE version. The other two (DE and DV) remain open. Some relevant results about the strength of special cases are in BGS. However, the local finiteness property that originally motivated this paper (Definition 3.5) fails for double rays in the DE and UE cases as can be seen by considering the star graph consisting of countably many copies of
$\mathbb {N}$
). Halin [Reference Halin11] proved the basic case here (UV) and BCP did the UE version. The other two (DE and DV) remain open. Some relevant results about the strength of special cases are in BGS. However, the local finiteness property that originally motivated this paper (Definition 3.5) fails for double rays in the DE and UE cases as can be seen by considering the star graph consisting of countably many copies of
![]() $\mathbb {Z}$
with one vertex common to all the copies. Thus these versions seemed less relevant to our concerns in this paper.
$\mathbb {Z}$
with one vertex common to all the copies. Thus these versions seemed less relevant to our concerns in this paper.
We now move on to the recursion theoretic notions needed to define THAs. Here we are working with the usual set
![]() $\mathbb {N}$
of natural numbers and understand notions such as well-orderings in the usual way—there simply are no descending chains. (As opposed to thinking of some model of arithmetic
$\mathbb {N}$
of natural numbers and understand notions such as well-orderings in the usual way—there simply are no descending chains. (As opposed to thinking of some model of arithmetic
![]() $\mathcal {N}$
with perhaps a nonstandard first order part or even a standard model, i.e.,
$\mathcal {N}$
with perhaps a nonstandard first order part or even a standard model, i.e.,
![]() $\mathcal {N}=\mathbb {N}$
but one in which the notion of well-foundedness for linear orderings as no descending chain in
$\mathcal {N}=\mathbb {N}$
but one in which the notion of well-foundedness for linear orderings as no descending chain in
![]() $S( \mathcal {N})$
is the not the same as no descending chain (possibly outside of
$S( \mathcal {N})$
is the not the same as no descending chain (possibly outside of
![]() $S(\mathcal {N})$
.) A standard reference for hyperarithmetic theory is [Reference Sacks26]. We give a brief list of the notions we need.
$S(\mathcal {N})$
.) A standard reference for hyperarithmetic theory is [Reference Sacks26]. We give a brief list of the notions we need.
Definition 2.7. We represent ordinals
![]() $\alpha $
as well-ordered relations on N. Typically such ordinal notations are endowed with various additional structures such as identifying
$\alpha $
as well-ordered relations on N. Typically such ordinal notations are endowed with various additional structures such as identifying
![]() $0$
, successor, and limit ordinals and specifying cofinal
$0$
, successor, and limit ordinals and specifying cofinal
![]() $\omega $
-sequences for the limit ordinals. An ordinal is recursive (in a set X) if it has a recursive (in X) representation. For a set X and ordinal (notation)
$\omega $
-sequences for the limit ordinals. An ordinal is recursive (in a set X) if it has a recursive (in X) representation. For a set X and ordinal (notation)
![]() $\alpha $
recursive in
$\alpha $
recursive in
![]() $ X$
, we define the transfinite iterations
$ X$
, we define the transfinite iterations
![]() $X^{\alpha }$
of the Turing jump of X by induction:
$X^{\alpha }$
of the Turing jump of X by induction:
![]() $X^{(0)}=X$
;
$X^{(0)}=X$
;
![]() $X^{(\alpha +1)}=(X^{\alpha })^{\prime }$
and for a limit ordinal
$X^{(\alpha +1)}=(X^{\alpha })^{\prime }$
and for a limit ordinal
![]() $\lambda $
,
$\lambda $
,
![]() $X^{(\lambda )}=\oplus \{X^{(\alpha )}|\alpha <\lambda \}$
(or as the sum over the
$X^{(\lambda )}=\oplus \{X^{(\alpha )}|\alpha <\lambda \}$
(or as the sum over the
![]() $X^{(\alpha )}$
in the specified cofinal sequence).
$X^{(\alpha )}$
in the specified cofinal sequence).
Definition 2.8.
![]() $HY\!P(X)$
, the collection of all sets hyperarithmetic in
$HY\!P(X)$
, the collection of all sets hyperarithmetic in
![]() $ X$
consists of those sets recursive in some
$ X$
consists of those sets recursive in some
![]() $X^{(\alpha )}$
for
$X^{(\alpha )}$
for
![]() $\alpha $
an ordinal recursive in X. These are also the sets
$\alpha $
an ordinal recursive in X. These are also the sets
![]() $\Delta _{1}^{1}$
in X.
$\Delta _{1}^{1}$
in X.
Definition 2.9. A sentence (theory) T is a theorem (theory) of hyperarithmetic analysis (THA) if:
-
1. for every
 $X\subseteq \mathbb {N}$
,
$X\subseteq \mathbb {N}$
,
 $(\mathbb {N},HY\!P(X))\vDash T$
and
$(\mathbb {N},HY\!P(X))\vDash T$
and -
2. for every
 $S\subseteq 2^{\mathbb {N}}$
, if
$S\subseteq 2^{\mathbb {N}}$
, if
 $(\mathbb {N},S)\vDash T$
and
$(\mathbb {N},S)\vDash T$
and
 $X\in S$
then
$X\in S$
then
 $HY\!P(X)\subseteq S$
.
$HY\!P(X)\subseteq S$
.
Definition 2.10. A theorem or theory T is an almost theorem (theory) of hyperarithmetic analysis
![]() $(ATHA)$
, if
$(ATHA)$
, if
![]() $T\nvdash $
ACA
$T\nvdash $
ACA
![]() $_{0}$
but
$_{0}$
but
![]() $T+ACA_{0}$
is a THA.
$T+ACA_{0}$
is a THA.
We now turn to defining and analyzing some mathematical and logical theorems that turn out to be ATHAs.
3 ATHA principles
We wish to consider the argument in BCP [top of page 2] that IRT
![]() $_{UE}$
follows from IRT
$_{UE}$
follows from IRT
![]() $_{UV}$
. We fill in their sketch to bring out the use of instances of
$_{UV}$
. We fill in their sketch to bring out the use of instances of
![]() $\Sigma _{1}^{1}$
-AC. They analyze only undirected graphs but the same arguments apply to directed ones so we present the two cases together.
$\Sigma _{1}^{1}$
-AC. They analyze only undirected graphs but the same arguments apply to directed ones so we present the two cases together.
Their proof can be presented as two lemmas:
Lemma 3.1. IRT
![]() $_{XE}$
restricted to locally finite graphs implies IRT
$_{XE}$
restricted to locally finite graphs implies IRT
![]() $_{XE}$
.
$_{XE}$
.
Lemma 3.2. IRT
![]() $_{XV}$
implies IRT
$_{XV}$
implies IRT
![]() $_{XE}$
restricted to locally finite graphs. In fact, IRT
$_{XE}$
restricted to locally finite graphs. In fact, IRT
![]() $_{XV}$
restricted to locally finite graphs implies IRT
$_{XV}$
restricted to locally finite graphs implies IRT
![]() $ _{XE}$
restricted to locally finite graphs.
$ _{XE}$
restricted to locally finite graphs.
The natural proof of Lemma 3.2 takes place in ACA
![]() $_{0}$
.
$_{0}$
.
Proof of Lemma 3.2 (ACA
 $_{0}$
)
$_{0}$
)
Let
![]() $G=\left \langle V,E\right \rangle $
be a locally finite graph with arbitrarily many E-disjoint rays. Consider the line graph
$G=\left \langle V,E\right \rangle $
be a locally finite graph with arbitrarily many E-disjoint rays. Consider the line graph
![]() $L(G)$
of G, i.e., the graph whose vertices are the edges of G and whose edges are the
$L(G)$
of G, i.e., the graph whose vertices are the edges of G and whose edges are the
![]() $ ((x,y),(y,z))$
for
$ ((x,y),(y,z))$
for
![]() $(x,y)\neq (y,z)\in E$
. As G is locally finite so is
$(x,y)\neq (y,z)\in E$
. As G is locally finite so is
![]() $ L(G)$
. (The only way a given
$ L(G)$
. (The only way a given
![]() $(u,v)$
can have an
$(u,v)$
can have an
![]() $(x,y)$
as a neighbor is if they have a vertex in common. So if
$(x,y)$
as a neighbor is if they have a vertex in common. So if
![]() $(u,v)$
had infinitely many neighbors, one of u or v would also have such in G.)
$(u,v)$
had infinitely many neighbors, one of u or v would also have such in G.)
A set of k many E-disjoint rays
![]() $R_{i}=\left \langle V_{i},E_{i}\right \rangle $
in G with isomorphisms
$R_{i}=\left \langle V_{i},E_{i}\right \rangle $
in G with isomorphisms
![]() $f_{i}$
produces k many V-disjoint rays
$f_{i}$
produces k many V-disjoint rays
![]() $\bar {R}_{i}$
with vertices
$\bar {R}_{i}$
with vertices
![]() $(x_{i,n},x_{i,n+1})$
in
$(x_{i,n},x_{i,n+1})$
in
![]() $ L(G)$
where we write
$ L(G)$
where we write
![]() $x_{i,n}$
for
$x_{i,n}$
for
![]() $f_{i}(n)$
. Applying the hypothesis of the lemma gives us infinitely many V-disjoint rays
$f_{i}(n)$
. Applying the hypothesis of the lemma gives us infinitely many V-disjoint rays
![]() $T_{i}$
with vertices
$T_{i}$
with vertices
![]() $ (x_{i,j},x_{i,j+1})$
in
$ (x_{i,j},x_{i,j+1})$
in
![]() $L(G)$
.
$L(G)$
.
Now we use the local finiteness of G to construct the required infinitely many E-disjoint rays
![]() $Q_{i}$
in
$Q_{i}$
in
![]() $G.$
Fix i and
$G.$
Fix i and
![]() $T=T_{i}$
and
$T=T_{i}$
and
![]() $ x_{j}=x_{i,j} $
. By the local finiteness of G, for every
$ x_{j}=x_{i,j} $
. By the local finiteness of G, for every
![]() $v\in V$
there are only finitely many n such that
$v\in V$
there are only finitely many n such that
![]() $v\in \{x_{n},x_{n+1}\}.$
(Otherwise, say v is
$v\in \{x_{n},x_{n+1}\}.$
(Otherwise, say v is
![]() $x_{n}$
for infinitely many n and then
$x_{n}$
for infinitely many n and then
![]() $(v,x_{n+1})$
is a vertex in the
$(v,x_{n+1})$
is a vertex in the
![]() $L(G)$
ray for all of these n. That means, however, that these edges are all distinct and so v has infinitely many neighbors in G for a contradiction.)
$L(G)$
ray for all of these n. That means, however, that these edges are all distinct and so v has infinitely many neighbors in G for a contradiction.)
We build
![]() $Q=Q_{i}$
by recursion starting with
$Q=Q_{i}$
by recursion starting with
![]() $a_{0}=x_{0}$
and let
$a_{0}=x_{0}$
and let
![]() $n_{0}$
be the largest n such that
$n_{0}$
be the largest n such that
![]() $a_{0}=x_{n}$
. Let
$a_{0}=x_{n}$
. Let
![]() $a_{1}=x_{n_{0}+1}$
so
$a_{1}=x_{n_{0}+1}$
so
![]() $ (a_{0},a_{1})\in E$
. Inductively, take
$ (a_{0},a_{1})\in E$
. Inductively, take
![]() $n_{k+1}$
(
$n_{k+1}$
(
![]() $>n_{k}$
) the largest n such that
$>n_{k}$
) the largest n such that
![]() $a_{k}=x_{n}$
and set
$a_{k}=x_{n}$
and set
![]() $a_{k+1}=x_{n_{k}+1}$
. (We can find this n by ACA
$a_{k+1}=x_{n_{k}+1}$
. (We can find this n by ACA
![]() $_{0}$
.) This recursion produces sequences
$_{0}$
.) This recursion produces sequences
![]() $n_{k},a_{k+1}$
with
$n_{k},a_{k+1}$
with
![]() $ Q=\left \langle a_{k}\right \rangle $
a ray in G and
$ Q=\left \langle a_{k}\right \rangle $
a ray in G and
![]() $(a_{n},a_{n+1})\in T$
for every n. Let this Q be
$(a_{n},a_{n+1})\in T$
for every n. Let this Q be
![]() $Q_{i}$
.
$Q_{i}$
.
Claim: The
![]() $Q_{i}$
are E-disjoint in G as required. If not, we have
$Q_{i}$
are E-disjoint in G as required. If not, we have
![]() $ (a_{i,n},a_{i,n+1})=(a_{j,m},a_{j,m+1})$
for some
$ (a_{i,n},a_{i,n+1})=(a_{j,m},a_{j,m+1})$
for some
![]() $i\neq j$
and n and m. However,
$i\neq j$
and n and m. However,
![]() $(a_{i,n},a_{i,n+1})\in T_{i}$
and
$(a_{i,n},a_{i,n+1})\in T_{i}$
and
![]() $(a_{j,m},a_{j,m+1})\in T_{j}$
contradicting the V-disjointness of the
$(a_{j,m},a_{j,m+1})\in T_{j}$
contradicting the V-disjointness of the
![]() $T_{i}$
in
$T_{i}$
in
![]() $L(G)$
.
$L(G)$
.
On the other hand, while the proof of Lemma 3.1 seems to also take place in ACA
![]() $_{0}$
, it, like that of IRT itself (BGS [Theorem 4.1]), relies on a use of
$_{0}$
, it, like that of IRT itself (BGS [Theorem 4.1]), relies on a use of
![]() $\Sigma _{1}^{1}$
-AC to get started.
$\Sigma _{1}^{1}$
-AC to get started.
Proof of Lemma 3.1 (
 $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
 $_{0}$
)
$_{0}$
)
We are given a graph
![]() $G=\left \langle V,E\right \rangle $
with arbitrarily many E-disjoint rays. By
$G=\left \langle V,E\right \rangle $
with arbitrarily many E-disjoint rays. By
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
choose a sequence
$_{0}$
choose a sequence
![]() $ S_{k}=\left \langle R_{k,1},\ldots ,R_{k,k}\right \rangle $
which consists, for each k, of k many E-disjoint rays in G. Now we construct the desired subgraph
$ S_{k}=\left \langle R_{k,1},\ldots ,R_{k,k}\right \rangle $
which consists, for each k, of k many E-disjoint rays in G. Now we construct the desired subgraph
![]() $G^{\prime }$
of
$G^{\prime }$
of
![]() $G.$
It has the same set of vertices
$G.$
It has the same set of vertices
![]() $ V=\{v_{i}|i\in N\}$
as G. We specify its edges by providing a recursive construction of sets
$ V=\{v_{i}|i\in N\}$
as G. We specify its edges by providing a recursive construction of sets
![]() $E_{i}$
of edges putting in a set of edges at each step. We guarantee that each
$E_{i}$
of edges putting in a set of edges at each step. We guarantee that each
![]() $E_{i}$
is a union of finitely many finite sets of E-disjoint rays in G and that after stage s no edge with a vertex
$E_{i}$
is a union of finitely many finite sets of E-disjoint rays in G and that after stage s no edge with a vertex
![]() $ v_{i}$
for
$ v_{i}$
for
![]() $i<s$
is ever put into E after stage s.
$i<s$
is ever put into E after stage s.
Begin at stage
![]() $0$
by putting all the edges in
$0$
by putting all the edges in
![]() $R_{1,1}$
into
$R_{1,1}$
into
![]() $E_{1}$
. Proceeding recursively at stage k we have
$E_{1}$
. Proceeding recursively at stage k we have
![]() $E_{k}$
and consider
$E_{k}$
and consider
![]() $ S_{k}=\left \langle R_{k,1},\ldots ,R_{k,k}\right \rangle $
. Each
$ S_{k}=\left \langle R_{k,1},\ldots ,R_{k,k}\right \rangle $
. Each
![]() $v_{j}$
for
$v_{j}$
for
![]() $ j<k$
appears in
$ j<k$
appears in
![]() $R_{k,i}$
at most once for each
$R_{k,i}$
at most once for each
![]() $i<k$
as
$i<k$
as
![]() $R_{k,i}$
is a ray. As we have the whole sequence of the
$R_{k,i}$
is a ray. As we have the whole sequence of the
![]() $S_{k}$
we can find (using only RCA
$S_{k}$
we can find (using only RCA
![]() $ _{0} $
) the
$ _{0} $
) the
![]() $i,j$
such that
$i,j$
such that
![]() $v_{j}\in R_{k,i}$
and the location n in the sequence where it occurs, say as
$v_{j}\in R_{k,i}$
and the location n in the sequence where it occurs, say as
![]() $x_{k,i,n_{j}}$
. We now put into
$x_{k,i,n_{j}}$
. We now put into
![]() $E_{k+1}$
all the edges appearing in any
$E_{k+1}$
all the edges appearing in any
![]() $R_{k,i}$
after all the
$R_{k,i}$
after all the
![]() $x_{k,i,n_{j}}$
for
$x_{k,i,n_{j}}$
for
![]() $ j<k$
which are defined. Let
$ j<k$
which are defined. Let
![]() $E^{\prime }=\cup E_{k}$
. As, for every k, we have put in a tail of each
$E^{\prime }=\cup E_{k}$
. As, for every k, we have put in a tail of each
![]() $R_{k,i}$
for
$R_{k,i}$
for
![]() $i<k$
into E
$i<k$
into E
![]() $_{k}$
we have guaranteed that
$_{k}$
we have guaranteed that
![]() $G^{\prime }=\left \langle V,E^{\prime }\right \rangle $
contains arbitrarily many E-disjoint rays.
$G^{\prime }=\left \langle V,E^{\prime }\right \rangle $
contains arbitrarily many E-disjoint rays.
Thus we only need to show that
![]() $G^{\prime }$
is locally finite. Consider any vertex
$G^{\prime }$
is locally finite. Consider any vertex
![]() $v_{k}$
. No edge containing
$v_{k}$
. No edge containing
![]() $v_{k}$
as a vertex is put in after stage k. On the other hand,
$v_{k}$
as a vertex is put in after stage k. On the other hand,
![]() $E_{k}$
is the union of finitely many finite sets of E-disjoint rays (all of which have been computed uniformly). Each set of E-disjoint rays in this union has
$E_{k}$
is the union of finitely many finite sets of E-disjoint rays (all of which have been computed uniformly). Each set of E-disjoint rays in this union has
![]() $v_{k}$
appearing at most once in each of its rays. Thus at most two edges containing
$v_{k}$
appearing at most once in each of its rays. Thus at most two edges containing
![]() $v_{k}$
appear in each of the finitely many rays in this set. Thus there are only finitely many edges containing
$v_{k}$
appear in each of the finitely many rays in this set. Thus there are only finitely many edges containing
![]() $v_{k}$
in each of the finite sets of E-disjoint making up
$v_{k}$
in each of the finite sets of E-disjoint making up
![]() $E_{k}$
. All in all, this makes only finitely many edges containing
$E_{k}$
. All in all, this makes only finitely many edges containing
![]() $v_{k}$
get put into
$v_{k}$
get put into
![]() $G^{\prime }$
. (In fact, we can compute the number of such edges in
$G^{\prime }$
. (In fact, we can compute the number of such edges in
![]() $ \mathcal {N}$
.)
$ \mathcal {N}$
.)
Now we study the crucial Lemma 3.1 that reduces the problem to locally finite graphs. We first prove that the IRT
![]() $_{XY}$
theorems for locally finite graphs are strictly weaker than the full theorems. Indeed, they are theorems of ACA
$_{XY}$
theorems for locally finite graphs are strictly weaker than the full theorems. Indeed, they are theorems of ACA
![]() $_{0\text {.}}$
$_{0\text {.}}$
Proposition 3.3 (ACA
 $_{0}$
).
$_{0}$
).
If G is a locally finite X-graph with arbitrarily many Y-disjoint rays then there is a sequence
![]() $\left \langle H_{n}\right \rangle $
of subgraphs of G with each
$\left \langle H_{n}\right \rangle $
of subgraphs of G with each
![]() $H_{n}$
consisting of n many disjoint rays. (This statement is SCR
$H_{n}$
consisting of n many disjoint rays. (This statement is SCR
![]() $_{XY}$
of Definition 5.5 for locally finite graphs.)
$_{XY}$
of Definition 5.5 for locally finite graphs.)
Proof Let
![]() $G=\left \langle V,E\right \rangle $
and
$G=\left \langle V,E\right \rangle $
and
![]() $V=\{v_{i}|i\in N\}$
. For each n and n-tuple
$V=\{v_{i}|i\in N\}$
. For each n and n-tuple
![]() $\left \langle v_{i_{j}}|j<n\right \rangle $
of distinct vertices of G consider the tree
$\left \langle v_{i_{j}}|j<n\right \rangle $
of distinct vertices of G consider the tree
![]() $T_{i,n}$
whose nodes are n-tuples of disjoint paths in G all of the length the height of the node in
$T_{i,n}$
whose nodes are n-tuples of disjoint paths in G all of the length the height of the node in
![]() $T_{i,n}$
. The root of
$T_{i,n}$
. The root of
![]() $T_{i,n}$
is
$T_{i,n}$
is
![]() $\left \langle v_{i_{j}}|j<n\right \rangle $
. If
$\left \langle v_{i_{j}}|j<n\right \rangle $
. If
![]() $\mu =\left \langle \sigma _{j}|j<n\right \rangle \in T_{i,n}$
then its immediate successors are all
$\mu =\left \langle \sigma _{j}|j<n\right \rangle \in T_{i,n}$
then its immediate successors are all
![]() $\nu =\left \langle \tau _{j}|j<n\right \rangle $
such that for each j,
$\nu =\left \langle \tau _{j}|j<n\right \rangle $
such that for each j,
![]() $\tau _{j}$
is an extension of
$\tau _{j}$
is an extension of
![]() $\sigma _{j}$
by one of the finitely many vertices v such that there is an edge from the last vertex in
$\sigma _{j}$
by one of the finitely many vertices v such that there is an edge from the last vertex in
![]() $\sigma _{j}$
to v and the
$\sigma _{j}$
to v and the
![]() $\tau _{j}$
are disjoint paths in G. As G is locally finite, the
$\tau _{j}$
are disjoint paths in G. As G is locally finite, the
![]() $T_{i,n}$
are finitely branching trees (recursive in
$T_{i,n}$
are finitely branching trees (recursive in
![]() $ G^{\prime }$
). Thus by ACA
$ G^{\prime }$
). Thus by ACA
![]() $_{0}$
(recursively in a few jumps of G) we can get the set of
$_{0}$
(recursively in a few jumps of G) we can get the set of
![]() $\left \langle i,n\right \rangle $
such that
$\left \langle i,n\right \rangle $
such that
![]() $T_{i,n}$
has a branch and, indeed, a sequence
$T_{i,n}$
has a branch and, indeed, a sequence
![]() $S_{i,n}$
each a branch in
$S_{i,n}$
each a branch in
![]() $T_{i,n}$
for each such
$T_{i,n}$
for each such
![]() $\left \langle i,n\right \rangle $
. Every such branch provides a subgraph
$\left \langle i,n\right \rangle $
. Every such branch provides a subgraph
![]() $G_{i,n}$
of G which consists of n disjoint rays. We can now just take the desired
$G_{i,n}$
of G which consists of n disjoint rays. We can now just take the desired
![]() $H_{n}$
to be
$H_{n}$
to be
![]() $G_{i,n}$
for the least i such that
$G_{i,n}$
for the least i such that
![]() $T_{i,n}$
has a branch.
$T_{i,n}$
has a branch.
Indeed we now have some equivalences.
Proposition 3.4. ACA
![]() $_{0}$
is equivalent to each IRT
$_{0}$
is equivalent to each IRT
![]() $_{XY}$
for locally finite graphs.
$_{XY}$
for locally finite graphs.
Proof To prove the implication from left to right, suppose G is a locally finite X-graph with arbitrarily many Y-disjoint rays. By Proposition 3.3 and BGS [Theorem 8.2], G has infinitely many Y-disjoint rays. For the other direction, note that the graphs used in BGS [Theorems 4.1, 4.2, and 5.9] to deduce ACA
![]() $_{0}$
from IRT
$_{0}$
from IRT
![]() $_{XY}$
are disjoint unions of finitely branching trees and so locally finite.
$_{XY}$
are disjoint unions of finitely branching trees and so locally finite.
Now we formulate a principle expressing the idea that one can reduce the problem of finding solutions to IRT to considering only the class of locally finite graphs. Of course, as the IRT
![]() $_{XY}$
are THAs and their restrictions to locally finite graphs are provable in ACA
$_{XY}$
are THAs and their restrictions to locally finite graphs are provable in ACA
![]() $_{0}$
, this reduction must be strong.
$_{0}$
, this reduction must be strong.
Definition 3.5.
LF
![]() $_{XY}$
is the principle that every X-graph which contains arbitrarily many Y-disjoint rays contains a locally finite subgraph which also contains arbitrarily many Y-disjoint rays.
$_{XY}$
is the principle that every X-graph which contains arbitrarily many Y-disjoint rays contains a locally finite subgraph which also contains arbitrarily many Y-disjoint rays.
We now work towards analyzing the complexity of the LF
![]() $_{XY}$
.
$_{XY}$
.
Proposition 3.6. In ACA
![]() $_{0}$
, LF
$_{0}$
, LF
![]() $_{XY}\rightarrow $
IRT
$_{XY}\rightarrow $
IRT
![]() $_{XY}$
.
$_{XY}$
.
Proof Suppose we are given a graph H with arbitrarily many disjoint rays. Let
![]() $ H^{\prime }$
be a locally finite subgraph with arbitrarily many rays. Again, Proposition 3.3 and Theorem 8.2 of BGS give us IRT
$ H^{\prime }$
be a locally finite subgraph with arbitrarily many rays. Again, Proposition 3.3 and Theorem 8.2 of BGS give us IRT
![]() $_{XY}$
.
$_{XY}$
.
In fact, over ACA
![]() $_{0}$
we have equivalences.
$_{0}$
we have equivalences.
Proposition 3.7. IRT
![]() $_{XY}{\rightarrow} $
LF
$_{XY}{\rightarrow} $
LF
![]() $_{XY}$
and so they are equivalent over ACA
$_{XY}$
and so they are equivalent over ACA
![]() $_{0}$
.
$_{0}$
.
Proof We are given a graph G with arbitrarily many disjoint rays and want to build a locally finite subgraph with the same property. We begin with the subgraph of the given graph consisting of infinitely many disjoint rays asserted to exist by IRT
![]() $_{XY}$
. As IRT
$_{XY}$
. As IRT
![]() $_{XY}\rightarrow $
ACA
$_{XY}\rightarrow $
ACA
![]() $_{0}$
(BGS [Theorem 5.1]), we can use ACA
$_{0}$
(BGS [Theorem 5.1]), we can use ACA
![]() $_{0}$
to thin out this subgraph so that our new nth ray is simply the nth given ray above the last time any vertex less than n appears in it. (Any vertex appears at most once in any ray.) Thus every vertex less than n appears in at most n many of these new rays. In each one it has edges to at most two other vertices. Thus it is a locally finite subgraph of the original graph and also contains infinitely many disjoint rays. The equivalence now follows from Proposition 3.6.
$_{0}$
to thin out this subgraph so that our new nth ray is simply the nth given ray above the last time any vertex less than n appears in it. (Any vertex appears at most once in any ray.) Thus every vertex less than n appears in at most n many of these new rays. In each one it has edges to at most two other vertices. Thus it is a locally finite subgraph of the original graph and also contains infinitely many disjoint rays. The equivalence now follows from Proposition 3.6.
Proposition 3.8. LF
![]() $_{XY}$
+ACA
$_{XY}$
+ACA
![]() $_{0}$
is a THA.
$_{0}$
is a THA.
Proof Each IRT
![]() $_{XY}$
is a THA by BGS [Theorem 5.1] and so we have the result by Proposition 3.7.
$_{XY}$
is a THA by BGS [Theorem 5.1] and so we have the result by Proposition 3.7.
We will see in Section 5 that none of the LF
![]() $_{XY}$
imply ACA
$_{XY}$
imply ACA
![]() $_{0}$
and so all are ATHAs.
$_{0}$
and so all are ATHAs.
4 A class of forcings for satisfying
 $\Pi _{2}^{1}$
principles
$\Pi _{2}^{1}$
principles
We define a class
![]() $\mathcal {C}$
of notions of forcing
$\mathcal {C}$
of notions of forcing
![]() $\mathcal {P}$
such that forcing with any one of them over a model
$\mathcal {P}$
such that forcing with any one of them over a model
![]() $\mathcal {N}=(N,S(\mathcal {N} ))$
of RCA
$\mathcal {N}=(N,S(\mathcal {N} ))$
of RCA
![]() $_{0}$
has several preservation type properties. (Our forcing language is flexible as to what else it might include for convenience but it does always include constants (as usual denoted by) n (or A) for each element of N (or
$_{0}$
has several preservation type properties. (Our forcing language is flexible as to what else it might include for convenience but it does always include constants (as usual denoted by) n (or A) for each element of N (or
![]() $S(\mathcal {N})$
). Note that these include class forcings in the sense that while each condition is (coded as) a set in
$S(\mathcal {N})$
). Note that these include class forcings in the sense that while each condition is (coded as) a set in
![]() $\mathcal {N}$
, the collection of conditions need not be (coded as) a set in
$\mathcal {N}$
, the collection of conditions need not be (coded as) a set in
![]() $\mathcal {N}$
nor even be definable over
$\mathcal {N}$
nor even be definable over
![]() $\mathcal {N}$
. Similarly, the dense sets we employ do not need to be definable over
$\mathcal {N}$
. Similarly, the dense sets we employ do not need to be definable over
![]() $\mathcal {N}$
. The requirement that the conditions themselves in be
$\mathcal {N}$
. The requirement that the conditions themselves in be
![]() $\mathcal {N}$
serves a couple of purposes. One is that it guarantees that when considering a countable model there are only countably many conditions which are used in the proof or Theorem 4.5 and elsewhere. It is also needed to see that many standard tree forcings are effective (Definition 4.2).
$\mathcal {N}$
serves a couple of purposes. One is that it guarantees that when considering a countable model there are only countably many conditions which are used in the proof or Theorem 4.5 and elsewhere. It is also needed to see that many standard tree forcings are effective (Definition 4.2).
Definition 4.1. A notion of forcing
![]() $\mathcal {P}=\left \langle P,\leq \right \rangle $
is a tree forcing (t-forcing) over
$\mathcal {P}=\left \langle P,\leq \right \rangle $
is a tree forcing (t-forcing) over
![]() $\mathcal {N}$
if the following hold:
$\mathcal {N}$
if the following hold:
-
1. Conditions in
 $\mathcal {P}$
are of the form
$\mathcal {P}$
are of the form
 $\left \langle \tau ,T\right \rangle $
where
$\left \langle \tau ,T\right \rangle $
where
 $T\in S(\mathcal {N})$
is a subtree of
$T\in S(\mathcal {N})$
is a subtree of
 $N^{<N}$
(i.e., a subset of
$N^{<N}$
(i.e., a subset of
 $N^{<N}$
in
$N^{<N}$
in
 $S(\mathcal {N})$
closed under initial segments with respect to
$S(\mathcal {N})$
closed under initial segments with respect to
 $\subseteq $
) and
$\subseteq $
) and
 $\tau $
is an element of T which is comparable with every
$\tau $
is an element of T which is comparable with every
 $\sigma \in T$
.
$\sigma \in T$
. -
2. If
 $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
then
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
then
 $\tau ^{\prime }\supseteq \tau $
and
$\tau ^{\prime }\supseteq \tau $
and
 $T^{\prime }\subseteq T$
,
$T^{\prime }\subseteq T$
, -
3. For every
 $n\in N$
the class
$n\in N$
the class
 $\{\left \langle \tau ,T\right \rangle ||\tau |\geq n\}$
is dense in
$\{\left \langle \tau ,T\right \rangle ||\tau |\geq n\}$
is dense in
 $\mathcal {P}$
, i.e.,
$\mathcal {P}$
, i.e.,
 $(\forall \left \langle \tau ,T\right \rangle \in \mathcal {P})(\exists \left \langle \tau ^{\prime },T^{\prime }\right \rangle )(\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle ~\&~|\tau ^{\prime }|\geq n)$
.
$(\forall \left \langle \tau ,T\right \rangle \in \mathcal {P})(\exists \left \langle \tau ^{\prime },T^{\prime }\right \rangle )(\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle ~\&~|\tau ^{\prime }|\geq n)$
.
Definition 4.2. A tree notion of forcing
![]() $\mathcal {P}$
is an effective tree forcing (et-forcing) if for every
$\mathcal {P}$
is an effective tree forcing (et-forcing) if for every
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {P}$
the class
$\left \langle \tau ,T\right \rangle \in \mathcal {P}$
the class
![]() $Ext(\left \langle \tau ,T\right \rangle )=\{\tau ^{\prime }|(\exists T^{\prime })(\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle )\}$
is
$Ext(\left \langle \tau ,T\right \rangle )=\{\tau ^{\prime }|(\exists T^{\prime })(\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle )\}$
is
![]() $\mathbf { \Sigma }_{1}^{0}$
, i.e., there is an
$\mathbf { \Sigma }_{1}^{0}$
, i.e., there is an
![]() $A\in S(N)$
such that
$A\in S(N)$
such that
![]() $Ext(\left \langle \tau ,T\right \rangle )$
is
$Ext(\left \langle \tau ,T\right \rangle )$
is
![]() $\Sigma _{1}^{0}(A)$
(over N).
$\Sigma _{1}^{0}(A)$
(over N).
Notation 4.3. If
![]() $\mathcal {G}$
is a filter on a t-forcing
$\mathcal {G}$
is a filter on a t-forcing
![]() $\mathcal {P}$
which is generic for a class
$\mathcal {P}$
which is generic for a class
![]() $\mathcal {D}$
of dense sets containing at least the
$\mathcal {D}$
of dense sets containing at least the
![]() $D_{n}=\{\left \langle \tau ,T\right \rangle ||\tau |\geq n\}$
, then the generic function
$D_{n}=\{\left \langle \tau ,T\right \rangle ||\tau |\geq n\}$
, then the generic function
![]() $G:N\mathbb {\rightarrow }N$
associated with
$G:N\mathbb {\rightarrow }N$
associated with
![]() $\mathcal {G}$
is
$\mathcal {G}$
is
![]() $\cup \{\tau |\exists T(\left \langle \tau ,T\right \rangle \in \mathcal {G\} }$
. We then say that G is
$\cup \{\tau |\exists T(\left \langle \tau ,T\right \rangle \in \mathcal {G\} }$
. We then say that G is
![]() $\mathcal {D}$
-generic on
$\mathcal {D}$
-generic on
![]() $\mathcal {P}$
. (Note that this G is always a function from N to N by the definitions of
$\mathcal {P}$
. (Note that this G is always a function from N to N by the definitions of
![]() $ \mathcal {P}$
being a t-forcing and of
$ \mathcal {P}$
being a t-forcing and of
![]() $\mathcal {G}$
being a
$\mathcal {G}$
being a
![]() $\mathcal {D}$
-generic filter on
$\mathcal {D}$
-generic filter on
![]() $\mathcal {P}$
.) We also say that a
$\mathcal {P}$
.) We also say that a
![]() $G:N\rightarrow N$
is on
$G:N\rightarrow N$
is on
![]() $\left \langle \tau ,T\right \rangle $
if
$\left \langle \tau ,T\right \rangle $
if
![]() $G\in \lbrack T]$
, i.e.,
$G\in \lbrack T]$
, i.e.,
![]() $\forall n(G\upharpoonright n\in T)$
. So if G is
$\forall n(G\upharpoonright n\in T)$
. So if G is
![]() $\{D_{n}\}$
-generic it is on every
$\{D_{n}\}$
-generic it is on every
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {G}$
.
$\left \langle \tau ,T\right \rangle \in \mathcal {G}$
.
We denote by
![]() $\mathcal {N}[G]$
the structure for second-order arithmetic with first order part the same as
$\mathcal {N}[G]$
the structure for second-order arithmetic with first order part the same as
![]() $\mathcal {N}$
(i.e., N) and second order part the closure of
$\mathcal {N}$
(i.e., N) and second order part the closure of
![]() $S(\mathcal {N})\cup \{G\}$
under
$S(\mathcal {N})\cup \{G\}$
under
![]() $\Delta _{1}^{0}$
-CA.
$\Delta _{1}^{0}$
-CA.
For
![]() $\sigma \in T$
,
$\sigma \in T$
,
![]() $T^{\sigma }=\{\rho \in T| \ \sigma \supseteq \rho \vee \rho \supseteq \sigma \}$
is what we call the tree T above
$T^{\sigma }=\{\rho \in T| \ \sigma \supseteq \rho \vee \rho \supseteq \sigma \}$
is what we call the tree T above
![]() $ \sigma $
.
$ \sigma $
.
Remark 4.4. There are a variety of ways to define forcing for models of second order arithmetic. Until the very last section of this paper we only need to consider forcing sentences of the form
![]() $\exists k\Phi (k,\bar {n} ,A,G) $
where
$\exists k\Phi (k,\bar {n} ,A,G) $
where
![]() $\Phi $
is formula with, if, one wants, bounded but certainly no unbounded quantifiers,
$\Phi $
is formula with, if, one wants, bounded but certainly no unbounded quantifiers,
![]() $\bar {n}\in N$
,
$\bar {n}\in N$
,
![]() $A\in S(\mathcal {N)}$
(and
$A\in S(\mathcal {N)}$
(and
![]() $ \exists k$
as its only unbounded quantifier) and perhaps some additional fixed recursive predicates. As usual we say
$ \exists k$
as its only unbounded quantifier) and perhaps some additional fixed recursive predicates. As usual we say
![]() $\left \langle \tau ,T\right \rangle \Vdash \exists k\Phi (k,\bar {n},A,G)$
if and only if there is a
$\left \langle \tau ,T\right \rangle \Vdash \exists k\Phi (k,\bar {n},A,G)$
if and only if there is a
![]() $k<|\tau |$
such that
$k<|\tau |$
such that
![]() $\tau $
contains all the information about G needed to guarantee the truth of
$\tau $
contains all the information about G needed to guarantee the truth of
![]() $\Phi (k,\bar {n},A,G)$
(even from the viewpoint of
$\Phi (k,\bar {n},A,G)$
(even from the viewpoint of
![]() $ \mathcal {N}$
). Guarantee here means that
$ \mathcal {N}$
). Guarantee here means that
![]() $\mathcal {N}[G]\vDash \Phi (k,\bar {n },A,G)$
for every
$\mathcal {N}[G]\vDash \Phi (k,\bar {n },A,G)$
for every
![]() $G\supseteq \tau $
. Thus we also write this as
$G\supseteq \tau $
. Thus we also write this as
![]() $\tau \Vdash \exists k\Phi (k,\bar {n},A,G)$
. Note that if
$\tau \Vdash \exists k\Phi (k,\bar {n},A,G)$
. Note that if
![]() $\mathcal {P}$
is an et-forcing then
$\mathcal {P}$
is an et-forcing then
![]() $\{\left \langle \tau ^{\prime },\bar {n}\right \rangle |\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )~\&~\tau ^{\prime }\Vdash \exists k\Phi (k,\bar {n},A,G)\}$
is
$\{\left \langle \tau ^{\prime },\bar {n}\right \rangle |\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )~\&~\tau ^{\prime }\Vdash \exists k\Phi (k,\bar {n},A,G)\}$
is
![]() $\mathbf {\Sigma }_{1}^{0}$
over
$\mathbf {\Sigma }_{1}^{0}$
over
![]() $ \mathcal {N}$
and all
$ \mathcal {N}$
and all
![]() $\mathbf {\Sigma }_{1}^{0}$
formulas over
$\mathbf {\Sigma }_{1}^{0}$
formulas over
![]() $\mathcal {N} [G] $
(with free variables) are equivalent to formulas of this form (with added free variables).
$\mathcal {N} [G] $
(with free variables) are equivalent to formulas of this form (with added free variables).
Personally, we like the recursion theoretic view that includes in the language a recursive predicates (with
![]() $\Delta _{1}^{0}$
definitions independent of
$\Delta _{1}^{0}$
definitions independent of
![]() $\mathcal {N}$
) for the pairing functions and a coding of finite strings
$\mathcal {N}$
) for the pairing functions and a coding of finite strings
![]() $\sigma $
with their length, the relation
$\sigma $
with their length, the relation
![]() $\sigma \subseteq X$
and the universal Turing functional
$\sigma \subseteq X$
and the universal Turing functional
![]() $\Phi (e,\sigma ,x,y)$
. Intuitively
$\Phi (e,\sigma ,x,y)$
. Intuitively
![]() $ \Phi (e,\sigma ,x,y)$
says that machine e with input x and using as an oracle only the finite sequence
$ \Phi (e,\sigma ,x,y)$
says that machine e with input x and using as an oracle only the finite sequence
![]() $\sigma $
converges with output y in at most
$\sigma $
converges with output y in at most
![]() $|\sigma |$
many steps. This, or any other similar coding procedure, provides a universal
$|\sigma |$
many steps. This, or any other similar coding procedure, provides a universal
![]() $\Sigma _{1}^{0}$
predicate, i.e., every
$\Sigma _{1}^{0}$
predicate, i.e., every
![]() $\Sigma _{1}^{0} $
predicate with set variable
$\Sigma _{1}^{0} $
predicate with set variable
![]() $X_{0},\ldots , X_{k}$
and number variables
$X_{0},\ldots , X_{k}$
and number variables
![]() $n_{0},\ldots , n_{l}$
is equivalent to
$n_{0},\ldots , n_{l}$
is equivalent to
![]() $\exists \sigma _{0},\ldots ,\sigma _{k}(\sigma _{0}\subseteq X_{0}\wedge \cdots \wedge \sigma _{k}\subseteq X_{k}~\wedge ~\Phi (e,\left \langle \sigma _{o},\ldots ,\sigma _{k}\right \rangle ,\left \langle n_{0},\ldots ,n_{l}\right \rangle ,1))$
where
$\exists \sigma _{0},\ldots ,\sigma _{k}(\sigma _{0}\subseteq X_{0}\wedge \cdots \wedge \sigma _{k}\subseteq X_{k}~\wedge ~\Phi (e,\left \langle \sigma _{o},\ldots ,\sigma _{k}\right \rangle ,\left \langle n_{0},\ldots ,n_{l}\right \rangle ,1))$
where
![]() $ e\in \mathbb {N}$
can be calculated recursively from the given
$ e\in \mathbb {N}$
can be calculated recursively from the given
![]() $\Sigma _{1}^{0}$
formula. As is common, we often write this as
$\Sigma _{1}^{0}$
formula. As is common, we often write this as
![]() $\Phi _{e}^{X_{0},\ldots ,X_{k}}(n_{0},\ldots , n_{l})=1$
. In this notation, for example, every set in
$\Phi _{e}^{X_{0},\ldots ,X_{k}}(n_{0},\ldots , n_{l})=1$
. In this notation, for example, every set in
![]() $\mathcal {N}[G]$
has its characteristic function of the form
$\mathcal {N}[G]$
has its characteristic function of the form
![]() $\Phi _{e}^{A\oplus G}$
for an
$\Phi _{e}^{A\oplus G}$
for an
![]() $A\in S(\mathcal {N})$
. Similarly,
$A\in S(\mathcal {N})$
. Similarly,
![]() $ \tau $
forcing a
$ \tau $
forcing a
![]() $\Sigma _{1}^{0}$
sentence of the forcing language (with, e.g., set parameter
$\Sigma _{1}^{0}$
sentence of the forcing language (with, e.g., set parameter
![]() $A\in S(\mathcal {N})$
and number parameter
$A\in S(\mathcal {N})$
and number parameter
![]() $n\in N$
) is equivalent to
$n\in N$
) is equivalent to
![]() $\mathcal {N}\vDash \Phi (e,A\upharpoonright |\tau |,\tau ,n,1)$
. These are essentially the only types of sentences we deal with until Section 7.
$\mathcal {N}\vDash \Phi (e,A\upharpoonright |\tau |,\tau ,n,1)$
. These are essentially the only types of sentences we deal with until Section 7.
We note that many common notions of forcing used to produce reals are et-forcings or easily seen to be equivalent to such. These include Cohen, Laver, Mathias, Sacks, and Silver forcing and many variations. Note that we need the fact that the conditions (trees) considered in any particular instance of one of these forcings are elements of the model to see that the forcings are effective. In this paper we use some of these as well as more specialized et-forcings in Section 5 to prove the conservation results that show, in particular, that the principles considered in Section 3 do not imply ACA
![]() $_{0}$
.
$_{0}$
.
Theorem 4.5. If
![]() $\mathcal {P}$
is an et-forcing over a countable model
$\mathcal {P}$
is an et-forcing over a countable model
![]() $ \mathcal {N}$
of
$ \mathcal {N}$
of
![]() $\mathrm {RCA}_{0}$
there is a countable collection
$\mathrm {RCA}_{0}$
there is a countable collection
![]() $\mathcal { D}$
of dense sets (including the ones specified in Definition 4.1) such that:
$\mathcal { D}$
of dense sets (including the ones specified in Definition 4.1) such that:
-
1. If G is
 $\mathcal {P}$
-generic for
$\mathcal {P}$
-generic for
 $\mathcal {D}$
, then
$\mathcal {D}$
, then
 $\mathcal {N} [G]\vDash \mathrm {RCA}_{0}$
.
$\mathcal {N} [G]\vDash \mathrm {RCA}_{0}$
. -
2. If R is a subtree of
 $N^{<N}$
(not necessarily in
$N^{<N}$
(not necessarily in
 $\mathcal {N}$
) with no branch in
$\mathcal {N}$
) with no branch in
 $\mathcal {N}$
, then there is a countable collection
$\mathcal {N}$
, then there is a countable collection
 $ \mathcal {D}^{\prime }\supseteq \mathcal {D}$
of dense sets such that for every G which is
$ \mathcal {D}^{\prime }\supseteq \mathcal {D}$
of dense sets such that for every G which is
 $\mathcal {P}$
-generic for
$\mathcal {P}$
-generic for
 $\mathcal {D}^{\prime }$
there is no branch of R in
$\mathcal {D}^{\prime }$
there is no branch of R in
 $\mathcal {N}[G]$
. We say that forcings with this property omit branches.
$\mathcal {N}[G]$
. We say that forcings with this property omit branches. -
3. If a forcing omits branches then for any countable collection
 $R_{i}$
of trees as in 2 (such as all those in
$R_{i}$
of trees as in 2 (such as all those in
 $\mathcal {N}$
) there is a single
$\mathcal {N}$
) there is a single
 $ \mathcal {D}^{\prime }$
as in 2 which works for every
$ \mathcal {D}^{\prime }$
as in 2 which works for every
 $R_{i}$
. In particular, for a set
$R_{i}$
. In particular, for a set
 $\{C_{i}|i\in \omega \}$
with
$\{C_{i}|i\in \omega \}$
with
 $C_{i}\subseteq N$
and
$C_{i}\subseteq N$
and
 $C_{i}\notin S(\mathcal {N)}$
for every
$C_{i}\notin S(\mathcal {N)}$
for every
 $i\in \omega $
, there is a
$i\in \omega $
, there is a
 $\mathcal {D}^{\prime }\supseteq \mathcal {D}$
such that, for any
$\mathcal {D}^{\prime }\supseteq \mathcal {D}$
such that, for any
 $\mathcal {D}^{\prime }$
-generic
$\mathcal {D}^{\prime }$
-generic
 $ G $
, no
$ G $
, no
 $C_{i}\in \mathcal {N}[G]$
. We say that forcings with this last property avoid cones.
$C_{i}\in \mathcal {N}[G]$
. We say that forcings with this last property avoid cones.
Proof The third clause follows immediately from the second by the countability of
![]() $ S(\mathcal {N})$
and then by taking
$ S(\mathcal {N})$
and then by taking
![]() $R_{i}=\{\rho \in N^{<N}|\rho \subset C_{i}\}$
. We prove each of the first two assertions by specifying the appropriate collections of dense sets.
$R_{i}=\{\rho \in N^{<N}|\rho \subset C_{i}\}$
. We prove each of the first two assertions by specifying the appropriate collections of dense sets.
1. By a classic result of Friedman [Reference Friedman8], it suffices to show that for any
![]() $\Sigma _{1}^{0}$
formula
$\Sigma _{1}^{0}$
formula
![]() $\exists k\Phi (k,m,A,G)$
with
$\exists k\Phi (k,m,A,G)$
with
![]() $A\in S( \mathcal {N})$
such that
$A\in S( \mathcal {N})$
such that
![]() $\mathcal {N}[G]\vDash \exists k\Phi (k,m,A,G)$
there is an
$\mathcal {N}[G]\vDash \exists k\Phi (k,m,A,G)$
there is an
![]() $\mathcal {N}$
-least
$\mathcal {N}$
-least
![]() $m^{\prime }$
such that
$m^{\prime }$
such that
![]() $\mathcal {N}[G]\vDash \exists k\Phi (k,m^{\prime },A,G)$
. By the definition of G there is a condition
$\mathcal {N}[G]\vDash \exists k\Phi (k,m^{\prime },A,G)$
. By the definition of G there is a condition
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {G}$
such that
$\left \langle \tau ,T\right \rangle \in \mathcal {G}$
such that
![]() $ \tau \Vdash \exists k\Phi (k,m,A,G)$
. We show that the conditions that guarantee that there is an
$ \tau \Vdash \exists k\Phi (k,m,A,G)$
. We show that the conditions that guarantee that there is an
![]() $\mathcal {N}$
-minimal such m are dense below
$\mathcal {N}$
-minimal such m are dense below
![]() $ \left \langle \tau ,T\right \rangle $
and so we can extend
$ \left \langle \tau ,T\right \rangle $
and so we can extend
![]() $\mathcal {D}$
to guarantee that
$\mathcal {D}$
to guarantee that
![]() $\mathcal {N}[G]\vDash $
RCA
$\mathcal {N}[G]\vDash $
RCA
![]() $_{0}$
as there are only countably many
$_{0}$
as there are only countably many
![]() $\Sigma _{1}^{0}$
formulas
$\Sigma _{1}^{0}$
formulas
![]() $\exists k\Phi (k,m,A,G)$
and conditions
$\exists k\Phi (k,m,A,G)$
and conditions
![]() $ \left \langle \tau ,T\right \rangle $
. As
$ \left \langle \tau ,T\right \rangle $
. As
![]() $\mathcal {P}$
is an et-forcing the set
$\mathcal {P}$
is an et-forcing the set
![]() $\{m^{\prime }\leq m|(\exists \tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )(\tau ^{\prime }\Vdash \exists k\Phi (k,m^{\prime },A,G))\}$
is
$\{m^{\prime }\leq m|(\exists \tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )(\tau ^{\prime }\Vdash \exists k\Phi (k,m^{\prime },A,G))\}$
is
![]() $\mathbf {\Sigma }_{1}^{0}$
in
$\mathbf {\Sigma }_{1}^{0}$
in
![]() $\mathcal {N}$
and so as
$\mathcal {N}$
and so as
![]() $\mathcal {N}\vDash $
RCA
$\mathcal {N}\vDash $
RCA
![]() $_{0}$
, there is an
$_{0}$
, there is an
![]() $\mathcal {N}$
-least such
$\mathcal {N}$
-least such
![]() $m^{\prime }$
with an associated
$m^{\prime }$
with an associated
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle $
. If
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle $
. If
![]() $ \mathcal {D}$
includes the corresponding dense set consisting of such
$ \mathcal {D}$
includes the corresponding dense set consisting of such
![]() $ \left \langle \tau ^{\prime },T^{\prime }\right \rangle $
for each
$ \left \langle \tau ^{\prime },T^{\prime }\right \rangle $
for each
![]() $ \left \langle \tau ,T\right \rangle $
, it is clear that
$ \left \langle \tau ,T\right \rangle $
, it is clear that
![]() $m^{\prime }$
is the least m such that
$m^{\prime }$
is the least m such that
![]() $\mathcal {N}[G^{\prime }]\vDash \exists k\Phi (k,m,A,G^{\prime })$
for any
$\mathcal {N}[G^{\prime }]\vDash \exists k\Phi (k,m,A,G^{\prime })$
for any
![]() $\mathcal {D}$
-generic
$\mathcal {D}$
-generic
![]() $G^{\prime }$
as desired. (Otherwise, there would be a
$G^{\prime }$
as desired. (Otherwise, there would be a
![]() $\left \langle \tau ^{\prime \prime },T^{\prime \prime }\right \rangle \leq \left \langle \tau ^{\prime },T^{\prime }\right \rangle , $
a
$\left \langle \tau ^{\prime \prime },T^{\prime \prime }\right \rangle \leq \left \langle \tau ^{\prime },T^{\prime }\right \rangle , $
a
![]() $k^{\prime }\in N$
, and an
$k^{\prime }\in N$
, and an
![]() $m^{\prime \prime }<_{\mathcal {N }}m^{\prime }$
such that
$m^{\prime \prime }<_{\mathcal {N }}m^{\prime }$
such that
![]() $\tau ^{\prime \prime }\Vdash \Phi (k^{\prime },m^{\prime \prime },A,G)$
.)
$\tau ^{\prime \prime }\Vdash \Phi (k^{\prime },m^{\prime \prime },A,G)$
.)
2. Consider any R as in the claim. We again want to specify the additional dense sets needed. Consider an arbitrary function in some
![]() $\mathcal {N}[G]$
. By the definition of
$\mathcal {N}[G]$
. By the definition of
![]() $\mathcal {N}[G]$
(and basic facts of about recursive functions true in RCA
$\mathcal {N}[G]$
(and basic facts of about recursive functions true in RCA
![]() $_{0}$
), it is of the form
$_{0}$
), it is of the form
![]() $\Phi _{e}^{A\oplus G}$
for some
$\Phi _{e}^{A\oplus G}$
for some
![]() $e\in N$
and
$e\in N$
and
![]() $A\in S(\mathcal {N})$
.
$A\in S(\mathcal {N})$
.
If for every
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {G}$
there is a
$\left \langle \tau ,T\right \rangle \in \mathcal {G}$
there is a
![]() $ \rho \notin R$
(
$ \rho \notin R$
(
![]() $\rho \in N^{<N}$
) and a
$\rho \in N^{<N}$
) and a
![]() $\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
such that
$\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
such that
![]() $\tau ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(l)=\rho (l)$
for every
$\tau ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(l)=\rho (l)$
for every
![]() $l<|\rho |$
then the set of conditions guaranteeing that
$l<|\rho |$
then the set of conditions guaranteeing that
![]() $\Phi _{e}^{A\oplus G}$
is not on R is dense. Thus we may assume that we have a
$\Phi _{e}^{A\oplus G}$
is not on R is dense. Thus we may assume that we have a
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {G}$
such that for every
$\left \langle \tau ,T\right \rangle \in \mathcal {G}$
such that for every
![]() $\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
and every
$\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
and every
![]() $\rho $
, if
$\rho $
, if
![]() $\tau ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(l)=\rho (l)$
for every
$\tau ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(l)=\rho (l)$
for every
![]() $l<|\rho |$
, then
$l<|\rho |$
, then
![]() $\rho \in R$
.
$\rho \in R$
.
Next, if there is a
![]() $\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
and an
$\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
and an
![]() $l\in N$
such that there is no
$l\in N$
such that there is no
![]() $m\in N$
and
$m\in N$
and
![]() $\tau ^{\prime \prime }\in Ext(\left \langle \tau ,T\right \rangle )$
with
$\tau ^{\prime \prime }\in Ext(\left \langle \tau ,T\right \rangle )$
with
![]() $\tau ^{\prime \prime }\supseteq \tau ^{\prime }$
such that
$\tau ^{\prime \prime }\supseteq \tau ^{\prime }$
such that
![]() $\tau ^{\prime \prime }\Vdash \Phi _{e}^{A\oplus G}(l)=m$
then the associated
$\tau ^{\prime \prime }\Vdash \Phi _{e}^{A\oplus G}(l)=m$
then the associated
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
guarantees that
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
guarantees that
![]() $\Phi _{e}^{A\oplus G}(l)\uparrow $
and so
$\Phi _{e}^{A\oplus G}(l)\uparrow $
and so
![]() $\Phi _{e}^{A\oplus G}$
is again not a branch on R. Thus we may assume that for every
$\Phi _{e}^{A\oplus G}$
is again not a branch on R. Thus we may assume that for every
![]() $l\in N$
and
$l\in N$
and
![]() $\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
there is an
$\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
there is an
![]() $m\in N$
and
$m\in N$
and
![]() $\tau ^{\prime \prime }\in Ext(\left \langle \tau ,T\right \rangle )$
with
$\tau ^{\prime \prime }\in Ext(\left \langle \tau ,T\right \rangle )$
with
![]() $\tau ^{\prime \prime }\supseteq \tau ^{\prime }$
such that
$\tau ^{\prime \prime }\supseteq \tau ^{\prime }$
such that
![]() $\tau ^{\prime \prime }\Vdash \Phi _{e}^{A\oplus G}(l)=m$
.
$\tau ^{\prime \prime }\Vdash \Phi _{e}^{A\oplus G}(l)=m$
.
We now prove that there is a branch f on R which is in
![]() $S(\mathcal {N})$
for a contradiction: By our last assumption on
$S(\mathcal {N})$
for a contradiction: By our last assumption on
![]() $\left \langle \tau ,T\right \rangle $
, we can define an
$\left \langle \tau ,T\right \rangle $
, we can define an
![]() $f:N\mathbb {\rightarrow }N$
by recursion in
$f:N\mathbb {\rightarrow }N$
by recursion in
![]() $\mathcal {N}$
starting with our
$\mathcal {N}$
starting with our
![]() $\left \langle \tau ,T\right \rangle $
and
$\left \langle \tau ,T\right \rangle $
and
![]() $ \tau _{-1}=\tau $
: We build sequences of
$ \tau _{-1}=\tau $
: We build sequences of
![]() $\tau _{l}\in Ext(\left \langle \tau ,T\right \rangle )$
and
$\tau _{l}\in Ext(\left \langle \tau ,T\right \rangle )$
and
![]() $m_{l}$
such that
$m_{l}$
such that
![]() $\tau _{l}\Vdash \Phi _{e}^{A\oplus G}(l)=m_{l}$
and
$\tau _{l}\Vdash \Phi _{e}^{A\oplus G}(l)=m_{l}$
and
![]() $\tau _{l}\subseteq \tau _{l+1}$
. This is a recursive procedure in
$\tau _{l}\subseteq \tau _{l+1}$
. This is a recursive procedure in
![]() $\mathcal {N}$
as
$\mathcal {N}$
as
![]() $\mathcal {P}$
is an et-forcing and so we can search for the next witnesses (and find them) effectively in
$\mathcal {P}$
is an et-forcing and so we can search for the next witnesses (and find them) effectively in
![]() $\mathcal {N}$
. By our first assumption on
$\mathcal {N}$
. By our first assumption on
![]() $\left \langle \tau ,T\right \rangle $
, the sequence
$\left \langle \tau ,T\right \rangle $
, the sequence
![]() $\left \langle m_{l}|l<n\right \rangle $
is in R for every
$\left \langle m_{l}|l<n\right \rangle $
is in R for every
![]() $n\in N$
and so f is the desired branch on R in
$n\in N$
and so f is the desired branch on R in
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
Another property of extensions of theories expressing weakness is having a minimal pair of extensions. We note that it follows from the cone avoiding property in an even stronger form.
Corollary 4.6. If
![]() $\mathcal {N}_{0}$
and
$\mathcal {N}_{0}$
and
![]() $\mathcal {N}_{1}$
are countable models of RCA
$\mathcal {N}_{1}$
are countable models of RCA
![]() $_{0}$
with the same first order part N,
$_{0}$
with the same first order part N,
![]() $\mathcal {P}_{0}$
and
$\mathcal {P}_{0}$
and
![]() $\mathcal {P}_{1}$
are et-forcings with classes
$\mathcal {P}_{1}$
are et-forcings with classes
![]() $\mathcal {D}_{0}$
and
$\mathcal {D}_{0}$
and
![]() $\mathcal {D}_{1}$
of dense sets as above (over
$\mathcal {D}_{1}$
of dense sets as above (over
![]() $\mathcal {N}_{0}$
and
$\mathcal {N}_{0}$
and
![]() $\mathcal {N}_{1}$
, respectively), then there are
$\mathcal {N}_{1}$
, respectively), then there are
![]() $G_{i}$
for
$G_{i}$
for
![]() $i=0,1$
which are
$i=0,1$
which are
![]() $\mathcal {D}_{i}$
-generic for
$\mathcal {D}_{i}$
-generic for
![]() $\mathcal {P}_{i}$
such that
$\mathcal {P}_{i}$
such that
![]() $\mathcal {N}_{0}[G_{0}],\mathcal {N} _{1}[G_{1}]\vDash RCA_{0}$
and
$\mathcal {N}_{0}[G_{0}],\mathcal {N} _{1}[G_{1}]\vDash RCA_{0}$
and
![]() $\mathcal {N}_{0}[G_{0}]\cap \mathcal {N} _{1}[G_{1}]=\mathcal {N}_{0}\cap \mathcal {N}_{1}$
. In fact, for any countable models
$\mathcal {N}_{0}[G_{0}]\cap \mathcal {N} _{1}[G_{1}]=\mathcal {N}_{0}\cap \mathcal {N}_{1}$
. In fact, for any countable models
![]() $\mathcal {N}\subseteq \mathcal {N}_{0}$
of RCA
$\mathcal {N}\subseteq \mathcal {N}_{0}$
of RCA
![]() $_{0}$
with the same first order part and
$_{0}$
with the same first order part and
![]() $\mathcal {P}$
an et-forcing over
$\mathcal {P}$
an et-forcing over
![]() $\mathcal {N}$
there is a countable collection
$\mathcal {N}$
there is a countable collection
![]() $\mathcal {D}$
of dense sets in
$\mathcal {D}$
of dense sets in
![]() $\mathcal {P}$
such that for any
$\mathcal {P}$
such that for any
![]() $\mathcal {D}$
-generic G,
$\mathcal {D}$
-generic G,
![]() $\mathcal {N}_{1}=\mathcal {N} [G]\vDash RCA_{0}$
and
$\mathcal {N}_{1}=\mathcal {N} [G]\vDash RCA_{0}$
and
![]() $\mathcal {N}_{0}\cap \mathcal {N}_{1}=\mathcal {N}$
. (Note that
$\mathcal {N}_{0}\cap \mathcal {N}_{1}=\mathcal {N}$
. (Note that
![]() $\mathcal {N}_{0}\cap \mathcal {N}_{1}$
denotes the second order structure whose first order part is N and second order part is
$\mathcal {N}_{0}\cap \mathcal {N}_{1}$
denotes the second order structure whose first order part is N and second order part is
![]() $S(\mathcal { N}_{0})\cap S(\mathcal {N}_{1})$
.)
$S(\mathcal { N}_{0})\cap S(\mathcal {N}_{1})$
.)
Proof Let
![]() $C_{i}$
list the subsets of N which are in
$C_{i}$
list the subsets of N which are in
![]() $\mathcal {N}_{0}$
but not in
$\mathcal {N}_{0}$
but not in
![]() $\mathcal {N}$
. Apply Theorem 4.5.3 to get the desired collection of dense sets.
$\mathcal {N}$
. Apply Theorem 4.5.3 to get the desired collection of dense sets.
From now on, in all the cases where we establish or use the omitting branches property similar definitions and conclusions can be made for avoiding cones and having minimal pairs of extensions. In particular, this applies to Definition 4.7, Theorems 4.13 and 6.2, and Corollary 7.6.
It is now standard to prove that any
![]() $\Pi _{2}^{1}$
principle
$\Pi _{2}^{1}$
principle
![]() $Q\equiv \ \forall X(\Phi (X)\rightarrow \exists Y\Psi (X,Y)$
with
$Q\equiv \ \forall X(\Phi (X)\rightarrow \exists Y\Psi (X,Y)$
with
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
arithmetic for which solutions can be provided by an et-forcing
$\Psi $
arithmetic for which solutions can be provided by an et-forcing
![]() $\mathcal {P}$
are
$\mathcal {P}$
are
![]() $\Pi _{1}^{1}$
and r-
$\Pi _{1}^{1}$
and r-
![]() $\Pi _{2}^{1}$
conservative over RCA
$\Pi _{2}^{1}$
conservative over RCA
![]() $_{0}$
. We formulate some relevant notions more generally for later use.
$_{0}$
. We formulate some relevant notions more generally for later use.
Definition 4.7. Let
![]() $Q\equiv \ \forall X(\Phi (X)\rightarrow \exists Y\Psi (X,Y))$
be a principle. Instances of Q are specified by an
$Q\equiv \ \forall X(\Phi (X)\rightarrow \exists Y\Psi (X,Y))$
be a principle. Instances of Q are specified by an
![]() $ X $
such that
$ X $
such that
![]() $\Phi (X)$
holds. A set
$\Phi (X)$
holds. A set
![]() $Y$
is a solution for the instance of Q specified by X if
$Y$
is a solution for the instance of Q specified by X if
![]() $\Psi (X,Y)$
holds. If
$\Psi (X,Y)$
holds. If
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are arithmetic we say Q is a
$\Psi $
are arithmetic we say Q is a
![]() $\Pi _{2}^{1}$
principle. We also consider sets or schemes of such sentences as principles in the obvious way. Note that we distinguish between principles and theories by subscripting with
$\Pi _{2}^{1}$
principle. We also consider sets or schemes of such sentences as principles in the obvious way. Note that we distinguish between principles and theories by subscripting with
![]() $0$
to denote the theory gotten by adding the principle to the axioms of RCA
$0$
to denote the theory gotten by adding the principle to the axioms of RCA
![]() $_{0}$
. Thus, for example, we denote the
$_{0}$
. Thus, for example, we denote the
![]() $\Pi _{2}^{1}$
principle that every infinite subtree
$\Pi _{2}^{1}$
principle that every infinite subtree
![]() $2^{<N}$
has an branch by WKL while WKL
$2^{<N}$
has an branch by WKL while WKL
![]() $_{0}$
is the standard theory gotten by adding this principle on to RCA
$_{0}$
is the standard theory gotten by adding this principle on to RCA
![]() $_{0}$
.
$_{0}$
.
-
1. We say that solutions to Q can be provided by forcing if, for every countable
 $\mathcal {N}\mathbf {\vDash }$
RCA
$\mathcal {N}\mathbf {\vDash }$
RCA
 $_{0}$
and instance of Q specified by an
$_{0}$
and instance of Q specified by an
 $X\in N$
, there is a notion of forcing
$X\in N$
, there is a notion of forcing
 $\mathcal {P}$
over
$\mathcal {P}$
over
 $\mathcal {N}$
and a countable collection
$\mathcal {N}$
and a countable collection
 $\mathcal {D}$
of dense subclasses of
$\mathcal {D}$
of dense subclasses of
 $\mathcal {P}$
such that for every
$\mathcal {P}$
such that for every
 $\mathcal {D}$
-generic G for
$\mathcal {D}$
-generic G for
 $\mathcal {P}$
,
$\mathcal {P}$
,
 $\mathcal {N}[G]\vDash $
RCA
$\mathcal {N}[G]\vDash $
RCA
 $_{0}~\&\ \exists Y\Psi (X,Y)$
.
$_{0}~\&\ \exists Y\Psi (X,Y)$
. -
2. We say that solutions can be added omitting branches to trees if the forcing
 $\mathcal {P}$
and dense sets
$\mathcal {P}$
and dense sets
 $\mathcal {D}$
can always be chosen so that, in addition, any subtree of
$\mathcal {D}$
can always be chosen so that, in addition, any subtree of
 $N^{<N}$
(of
$N^{<N}$
(of
 $\mathcal {N}$
) that has no branch in
$\mathcal {N}$
) that has no branch in
 $S(\mathcal {N})$
has no branch in
$S(\mathcal {N})$
has no branch in
 $\mathcal {N}[G]$
.
$\mathcal {N}[G]$
.
One can now prove by fairly standard methods that providing solutions by the various types of forcing insures specific conservation results and other evidences of the weakness of the given principle. We extend the usual arguments for conservation results to cover larger classes of formulas that we now describe.
Definition 4.8. If
![]() $\Gamma $
is a class of sentences and T a theory of second order arithmetic, we say T is
$\Gamma $
is a class of sentences and T a theory of second order arithmetic, we say T is
![]() $\Gamma $
conservative (over RCA
$\Gamma $
conservative (over RCA
![]() $_{0}$
), if for every
$_{0}$
), if for every
![]() $\Lambda \in \Gamma $
such that
$\Lambda \in \Gamma $
such that
![]() $T\vdash \Lambda $
, RCA
$T\vdash \Lambda $
, RCA
![]() $ _{0}\vdash \Lambda $
.
$ _{0}\vdash \Lambda $
.
Definition 4.9. A theory T is
![]() $\Pi _{1}^{1}$
conservative if it is conservative for the class of sentences
$\Pi _{1}^{1}$
conservative if it is conservative for the class of sentences
![]() $\Lambda $
of the form
$\Lambda $
of the form
![]() $\forall X\Phi (X)$
with
$\forall X\Phi (X)$
with
![]() $\Phi $
arithmetic. We extend this to G-
$\Phi $
arithmetic. We extend this to G-
![]() $\Pi _{1}^{1}$
, generalized
$\Pi _{1}^{1}$
, generalized
![]() $\Pi _{1}^{1}$
, conservative by including all sentences
$\Pi _{1}^{1}$
, conservative by including all sentences
![]() $\Lambda $
in the G-
$\Lambda $
in the G-
![]() $\Pi _{1}^{1}$
class of formulas defined by closing the quantifier free formulas under conjunction (
$\Pi _{1}^{1}$
class of formulas defined by closing the quantifier free formulas under conjunction (
![]() $\wedge $
), disjunction (
$\wedge $
), disjunction (
![]() $\vee $
), first order quantification (
$\vee $
), first order quantification (
![]() $ \forall x$
and
$ \forall x$
and
![]() $\exists x$
for number variables), and universal second order quantification (
$\exists x$
for number variables), and universal second order quantification (
![]() $\forall X$
for set variables).
$\forall X$
for set variables).
Definition 4.10. Hirschfeldt, Shore, and Slaman [Reference Hirschfeldt, Shore and Slaman15, Corollary 3.15] define r -
![]() $\Pi _{2}^{1}$
conservativity by the class of sentences
$\Pi _{2}^{1}$
conservativity by the class of sentences
![]() $ \Lambda $
of the form
$ \Lambda $
of the form
![]() $\forall X(\Phi (X)\rightarrow \exists Y\Theta (X,Y))$
where
$\forall X(\Phi (X)\rightarrow \exists Y\Theta (X,Y))$
where
![]() $\Phi $
is arithmetic and
$\Phi $
is arithmetic and
![]() $\Theta $
is
$\Theta $
is
![]() $\Sigma _{3}^{0}$
. We extend this to G-r-
$\Sigma _{3}^{0}$
. We extend this to G-r-
![]() $\Pi _{2}^{1}$
conservativity by including all sentences in the G- r-
$\Pi _{2}^{1}$
conservativity by including all sentences in the G- r-
![]() $\Pi _{2}^{1}$
class of formulas defined by closing all formulas which are either quantifier free or of the form
$\Pi _{2}^{1}$
class of formulas defined by closing all formulas which are either quantifier free or of the form
![]() $\exists Y\Theta (Y)$
where
$\exists Y\Theta (Y)$
where
![]() $\Theta $
is
$\Theta $
is
![]() $ \Sigma _{3}^{0}$
under the same operations as in the definition of G-
$ \Sigma _{3}^{0}$
under the same operations as in the definition of G-
![]() $\Pi _{1}^{1}$
(
$\Pi _{1}^{1}$
(
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
,
$\vee $
,
![]() $\forall x$
,
$\forall x$
,
![]() $\exists x$
, and
$\exists x$
, and
![]() $\forall X$
). Note that the G- r-
$\forall X$
). Note that the G- r-
![]() $\Pi _{2}^{1}$
class of formulas contains the G-
$\Pi _{2}^{1}$
class of formulas contains the G-
![]() $\Pi _{1}^{1}$
class of formulas and so G - r-
$\Pi _{1}^{1}$
class of formulas and so G - r-
![]() $\Pi _{2}^{1}$
conservativity implies G-
$\Pi _{2}^{1}$
conservativity implies G-
![]() $ \Pi _{1}^{1}$
conservativity.
$ \Pi _{1}^{1}$
conservativity.
We introduce other classes of conservativity results related to sentences of the form
![]() $\forall X\exists !Y\Phi (X,Y)$
for
$\forall X\exists !Y\Phi (X,Y)$
for
![]() $\Phi $
arithmetic in Section 7. They require additional uniformity type conditions on our et-forcings.
$\Phi $
arithmetic in Section 7. They require additional uniformity type conditions on our et-forcings.
All of our proofs of conservation results have the same general format. We have a class
![]() $\Gamma $
of formulas and a theory T of second order arithmetic. We want to prove T is conservative (over RCA
$\Gamma $
of formulas and a theory T of second order arithmetic. We want to prove T is conservative (over RCA
![]() $_{0}$
) for sentences in
$_{0}$
) for sentences in
![]() $\Gamma $
. For the sake of a contradiction, we assume that there is a sentence
$\Gamma $
. For the sake of a contradiction, we assume that there is a sentence
![]() $\Lambda \in \Gamma $
such that
$\Lambda \in \Gamma $
such that
![]() $T\vdash \Lambda $
and a countable model
$T\vdash \Lambda $
and a countable model
![]() $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
![]() $_{0}$
such that
$_{0}$
such that
![]() $\mathcal {N}\vDash \lnot \Lambda $
. We then construct, by iterated forcing, a model
$\mathcal {N}\vDash \lnot \Lambda $
. We then construct, by iterated forcing, a model
![]() $\mathcal {N} _{\infty }$
of T. In each case, we have a notion of forcing that adds solutions for all the sentences of T, e.g., of
$\mathcal {N} _{\infty }$
of T. In each case, we have a notion of forcing that adds solutions for all the sentences of T, e.g., of
![]() $\Pi _{2}^{1}$
principles Q. We construct a limit ordinal length iteration of forcings producing witnesses for the solutions for these principle. For
$\Pi _{2}^{1}$
principles Q. We construct a limit ordinal length iteration of forcings producing witnesses for the solutions for these principle. For
![]() $\Pi _{2}^{1}$
principles these have length
$\Pi _{2}^{1}$
principles these have length
![]() $\omega $
but other lengths will be used and we denote the length ambiguously by
$\omega $
but other lengths will be used and we denote the length ambiguously by
![]() $\infty $
. This gives us a sequence of models
$\infty $
. This gives us a sequence of models
![]() $\mathcal {N}_{i+i}=\mathcal {N}_{i}[G_{i}]$
and
$\mathcal {N}_{i+i}=\mathcal {N}_{i}[G_{i}]$
and
![]() $\mathcal {N}_{\lambda }=(N,\cup \{S(\mathcal {N}_{\alpha })|\alpha <\lambda \}$
of RCA
$\mathcal {N}_{\lambda }=(N,\cup \{S(\mathcal {N}_{\alpha })|\alpha <\lambda \}$
of RCA
![]() $_{0}$
(all with the same first order part N) such that
$_{0}$
(all with the same first order part N) such that
![]() $\mathcal {N}_{\infty }=(N,\cup \{S(\mathcal {N}_{i})|i<\infty \})$
is a model of RCA
$\mathcal {N}_{\infty }=(N,\cup \{S(\mathcal {N}_{i})|i<\infty \})$
is a model of RCA
![]() $_{0}+T$
by arranging that every instance of the principles Q of T specified by an X in some
$_{0}+T$
by arranging that every instance of the principles Q of T specified by an X in some
![]() $\mathcal {N}_{i}$
is given a solution Y in some later
$\mathcal {N}_{i}$
is given a solution Y in some later
![]() $\mathcal {N}_{j}$
.
$\mathcal {N}_{j}$
.
Next, we argue that
![]() $\mathcal {N}_{\infty }\vDash \lnot \Lambda $
as well for a contradiction. We prove that the truth of
$\mathcal {N}_{\infty }\vDash \lnot \Lambda $
as well for a contradiction. We prove that the truth of
![]() $\lnot \Lambda $
is preserved for all sentences
$\lnot \Lambda $
is preserved for all sentences
![]() $\Lambda \in \Gamma $
with constants from N and
$\Lambda \in \Gamma $
with constants from N and
![]() $S(N)$
by an induction on the complexity of
$S(N)$
by an induction on the complexity of
![]() $\Lambda $
. The argument can be seen as playing a game between the two models to eliminate number quantifiers or universal set quantifiers as well as the positive connectives. This will then complete each proof of conservativity that we provide.
$\Lambda $
. The argument can be seen as playing a game between the two models to eliminate number quantifiers or universal set quantifiers as well as the positive connectives. This will then complete each proof of conservativity that we provide.
Theorem 4.11. If solutions to a
![]() $\Pi _{2}^{1}$
principle Q can be provided by forcing, then RCA
$\Pi _{2}^{1}$
principle Q can be provided by forcing, then RCA
![]() $_{0}+Q$
is G-
$_{0}+Q$
is G-
![]() $\Pi _{1}^{1}$
conservative over RCA
$\Pi _{1}^{1}$
conservative over RCA
![]() $_{0}.$
$_{0}.$
Proof We begin the plan outlined above with quantifier free G-
![]() $\Pi _{1}^{1}$
sentences
$\Pi _{1}^{1}$
sentences
![]() $\Lambda $
with constants from N and
$\Lambda $
with constants from N and
![]() $S(\mathcal {N})$
. Here the truth of both
$S(\mathcal {N})$
. Here the truth of both
![]() $\Lambda $
and
$\Lambda $
and
![]() $\lnot \Lambda $
are preserved from
$\lnot \Lambda $
are preserved from
![]() $\mathcal {N} $
to
$\mathcal {N} $
to
![]() $\mathcal {N}_{\infty }$
as
$\mathcal {N}_{\infty }$
as
![]() $N=N_{\infty }$
and
$N=N_{\infty }$
and
![]() $S(\mathcal {N})\subseteq S(\mathcal {N}_{\infty })$
. Suppose next that
$S(\mathcal {N})\subseteq S(\mathcal {N}_{\infty })$
. Suppose next that
![]() $\Lambda =\Delta _{0}\wedge \Delta _{1}$
. As
$\Lambda =\Delta _{0}\wedge \Delta _{1}$
. As
![]() $\mathcal {N}\vDash \lnot \Lambda $
,
$\mathcal {N}\vDash \lnot \Lambda $
,
![]() $\mathcal {N}\vDash \lnot \Delta _{i}$
for at least one
$\mathcal {N}\vDash \lnot \Delta _{i}$
for at least one
![]() $i\in \{0,1\}$
. By induction then
$i\in \{0,1\}$
. By induction then
![]() $ \mathcal {N}_{\infty }\vDash \lnot \Delta _{i}$
as well as required. If
$ \mathcal {N}_{\infty }\vDash \lnot \Delta _{i}$
as well as required. If
![]() $ \Lambda =\Delta _{0}\vee \Delta _{1}$
and
$ \Lambda =\Delta _{0}\vee \Delta _{1}$
and
![]() $\mathcal {N}\vDash \lnot \Lambda $
then
$\mathcal {N}\vDash \lnot \Lambda $
then
![]() $\mathcal {N}\vDash \lnot \Delta _{0}\wedge \lnot \Delta _{1}$
and so by induction
$\mathcal {N}\vDash \lnot \Delta _{0}\wedge \lnot \Delta _{1}$
and so by induction
![]() $\mathcal {N}_{\infty }\vDash \lnot \Delta _{0}\wedge \lnot \Delta _{1}$
and
$\mathcal {N}_{\infty }\vDash \lnot \Delta _{0}\wedge \lnot \Delta _{1}$
and
![]() $\mathcal {N}_{\infty }\vDash \lnot (\Delta _{0}\vee \Delta _{1})$
as required. Next, suppose
$\mathcal {N}_{\infty }\vDash \lnot (\Delta _{0}\vee \Delta _{1})$
as required. Next, suppose
![]() $\Lambda =\forall x\Delta (x)$
and
$\Lambda =\forall x\Delta (x)$
and
![]() $\mathcal {N} \vDash \lnot \Lambda $
. Choose an
$\mathcal {N} \vDash \lnot \Lambda $
. Choose an
![]() $n\in N$
such that
$n\in N$
such that
![]() $\mathcal {N}\vDash \lnot \Delta (n)$
. By induction,
$\mathcal {N}\vDash \lnot \Delta (n)$
. By induction,
![]() $\mathcal {N}_{\infty }\vDash \lnot \Delta (n)$
and so
$\mathcal {N}_{\infty }\vDash \lnot \Delta (n)$
and so
![]() $\mathcal {N}_{\infty }\vDash \lnot \forall x\Delta (x)$
. Suppose
$\mathcal {N}_{\infty }\vDash \lnot \forall x\Delta (x)$
. Suppose
![]() $\Lambda =\exists x\Delta (x)$
and
$\Lambda =\exists x\Delta (x)$
and
![]() $\mathcal {N}\vDash \lnot \Lambda $
. If
$\mathcal {N}\vDash \lnot \Lambda $
. If
![]() $ \mathcal {N}_{\infty }\vDash \exists x\Delta (x)$
choose a witness
$ \mathcal {N}_{\infty }\vDash \exists x\Delta (x)$
choose a witness
![]() $n\in N_{\infty }=N$
so that
$n\in N_{\infty }=N$
so that
![]() $\mathcal {N}_{\infty }\vDash \Delta (n)$
. As
$\mathcal {N}_{\infty }\vDash \Delta (n)$
. As
![]() $\Delta (n)$
is also a sentence in
$\Delta (n)$
is also a sentence in
![]() $\Gamma $
, we have that
$\Gamma $
, we have that
![]() $\mathcal {N}\vDash \Delta (n)$
by induction for the desired contradiction. Finally, if
$\mathcal {N}\vDash \Delta (n)$
by induction for the desired contradiction. Finally, if
![]() $\Lambda =\forall X\Delta (X)$
and
$\Lambda =\forall X\Delta (X)$
and
![]() $\mathcal {N}\vDash \lnot \Lambda $
, choose a
$\mathcal {N}\vDash \lnot \Lambda $
, choose a
![]() $W\in S(\mathcal {N})$
such that
$W\in S(\mathcal {N})$
such that
![]() $\mathcal {N}\vDash \lnot \Delta (W)$
. As
$\mathcal {N}\vDash \lnot \Delta (W)$
. As
![]() $\Delta (W)$
is a sentence in
$\Delta (W)$
is a sentence in
![]() $\Gamma $
, we again have
$\Gamma $
, we again have
![]() $\mathcal {N}_{\infty }\vDash \lnot \Delta (W)$
as required.
$\mathcal {N}_{\infty }\vDash \lnot \Delta (W)$
as required.
Similarly, we can prove a G-r-
![]() $\Pi _{2}^{1}$
conservation result for such Q when solutions are provided by et-forcings using Theorem 4.5.2.
$\Pi _{2}^{1}$
conservation result for such Q when solutions are provided by et-forcings using Theorem 4.5.2.
Theorem 4.12. If solutions to a
![]() $\Pi _{2}^{1}$
principle Q can be provided omitting branches, then RCA
$\Pi _{2}^{1}$
principle Q can be provided omitting branches, then RCA
![]() $_{0}+Q$
is G-r-
$_{0}+Q$
is G-r-
![]() $\Pi _{2}^{1}$
conservative over RCA
$\Pi _{2}^{1}$
conservative over RCA
![]() $_{0}$
.
$_{0}$
.
Proof The argument for quantifier free sentences is as in Theorem 4.11 as are the inductive cases for
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
,
$\vee $
,
![]() $\exists x$
,
$\exists x$
,
![]() $\forall x$
, and
$\forall x$
, and
![]() $\forall X$
. Here we also have to begin with sentences
$\forall X$
. Here we also have to begin with sentences
![]() $ \Lambda $
of the form
$ \Lambda $
of the form
![]() $\exists Y\Theta (\bar {x},\bar {y},Y)$
with
$\exists Y\Theta (\bar {x},\bar {y},Y)$
with
![]() $\Theta $
a
$\Theta $
a
![]() $\Sigma _{3}^{0}$
formula with constants from N and
$\Sigma _{3}^{0}$
formula with constants from N and
![]() $S(\mathcal {N})$
and suppose that
$S(\mathcal {N})$
and suppose that
![]() $\mathcal {N}\vDash \lnot \Lambda $
. As in [Reference Hirschfeldt, Shore and Slaman15, last paragraph of page 5818], the point here is that for any model
$\mathcal {N}\vDash \lnot \Lambda $
. As in [Reference Hirschfeldt, Shore and Slaman15, last paragraph of page 5818], the point here is that for any model
![]() $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
![]() $_{0}$
the failure of a sentence
$_{0}$
the failure of a sentence
![]() $\exists Y\Theta (Y)$
with
$\exists Y\Theta (Y)$
with
![]() $\Theta $
being
$\Theta $
being
![]() $\Sigma _{3}^{0}$
(with set constants
$\Sigma _{3}^{0}$
(with set constants
![]() $\bar {W}$
) is equivalent to their being, for each
$\bar {W}$
) is equivalent to their being, for each
![]() $k\in N$
, a specifically defined tree
$k\in N$
, a specifically defined tree
![]() $T_{k}$
(recursive in
$T_{k}$
(recursive in
![]() $\bar {W}$
) which has no branch in the model. Thus none of these trees has a branch in
$\bar {W}$
) which has no branch in the model. Thus none of these trees has a branch in
![]() $\mathcal {N}$
and so by our assumptions on the forcings none in
$\mathcal {N}$
and so by our assumptions on the forcings none in
![]() $\mathcal {N}_{\infty }$
either. Thus
$\mathcal {N}_{\infty }$
either. Thus
![]() $\mathcal {N} _{\omega }\vDash \lnot \exists Y\Theta (\bar {x},\bar {y}.Y)$
as required.
$\mathcal {N} _{\omega }\vDash \lnot \exists Y\Theta (\bar {x},\bar {y}.Y)$
as required.
We next note the analog of these conservation results for forcings omitting branches.
Theorem 4.13. If Q is a
![]() $\Pi _{2}^{1}$
principle such that solutions can be added omitting branches, i.e., if
$\Pi _{2}^{1}$
principle such that solutions can be added omitting branches, i.e., if
![]() $\mathcal {N}\vDash $
RCA
$\mathcal {N}\vDash $
RCA
![]() $_{0}$
is countable,
$_{0}$
is countable,
![]() $\{R_{j}|j\in \omega \}\subseteq S(\mathcal {N})$
and
$\{R_{j}|j\in \omega \}\subseteq S(\mathcal {N})$
and
![]() $\forall j\in \omega (R_{j}$
is a subtree of the
$\forall j\in \omega (R_{j}$
is a subtree of the
![]() $N^{<N}$
of
$N^{<N}$
of
![]() $\mathcal {N}$
without a branch in
$\mathcal {N}$
without a branch in
![]() $\mathcal {N})$
, then there is an extension
$\mathcal {N})$
, then there is an extension
![]() $\mathcal {N}^{\prime }$
of
$\mathcal {N}^{\prime }$
of
![]() $\mathcal {N}$
with the same first order part such that
$\mathcal {N}$
with the same first order part such that
![]() $\mathcal {N} ^{\prime }\vDash Q+$
RCA
$\mathcal {N} ^{\prime }\vDash Q+$
RCA
![]() $_{0}$
and no
$_{0}$
and no
![]() $R_{j}$
has a branch in
$R_{j}$
has a branch in
![]() $S(\mathcal {N} ^{\prime })$
.
$S(\mathcal {N} ^{\prime })$
.
Proof As there are here no conservation results to verify the proof is simply the basic argument given above for the construction. Then one simply notes that by the choice of forcings no branch is added on for any
![]() $R_{i}$
at any successor step and so none enter at a limit level either.
$R_{i}$
at any successor step and so none enter at a limit level either.
We now note that by interspersing the appropriate forcings in the iterations, the class of problems described in each of the two clauses of Definition 4.7 (and so also cone avoiding and minimal pair extension) are closed under conjunction. Indeed, if they hold for each
![]() $ Q_{i} $
for
$ Q_{i} $
for
![]() $i\in \omega $
they hold for the theory
$i\in \omega $
they hold for the theory
![]() $T=\{Q_{i}|i\in \omega \} $
. So to then do the conservation results for G-
$T=\{Q_{i}|i\in \omega \} $
. So to then do the conservation results for G-
![]() $\Pi _{1}^{1}$
(Theorem 4.11) and G-r-
$\Pi _{1}^{1}$
(Theorem 4.11) and G-r-
![]() $\Pi _{1}^{1}$
(Theorem 4.12) via extensions constructed omitting branches and avoiding cones. Thus we can add on any principle with solutions given by et-forcings such as COH [Reference Cholak, Jockusch and Slaman4, Theorem 9.1] and [Reference Hirschfeldt and Shore14, Theorem 2.21] (Mathias forcing); AMT [Reference Hirschfeldt, Shore and Slaman15, Corollary 3.15] as well as BCT-II and RCA
$\Pi _{1}^{1}$
(Theorem 4.12) via extensions constructed omitting branches and avoiding cones. Thus we can add on any principle with solutions given by et-forcings such as COH [Reference Cholak, Jockusch and Slaman4, Theorem 9.1] and [Reference Hirschfeldt and Shore14, Theorem 2.21] (Mathias forcing); AMT [Reference Hirschfeldt, Shore and Slaman15, Corollary 3.15] as well as BCT-II and RCA
![]() $_{0}^{+}$
of Brown and Simpson [Reference Brown and Simpson3, Section 4 and Corollary 6.5] and
$_{0}^{+}$
of Brown and Simpson [Reference Brown and Simpson3, Section 4 and Corollary 6.5] and
![]() $\Pi _{\infty }^{0}G=\cup \Pi _{n}^{0}G$
in the terminology of Hirschfeldt, Lange, and Shore [Reference Hirschfeldt, Lange and Shore13, p. 89]
$\Pi _{\infty }^{0}G=\cup \Pi _{n}^{0}G$
in the terminology of Hirschfeldt, Lange, and Shore [Reference Hirschfeldt, Lange and Shore13, p. 89]
![]() $\Pi _{\infty }^{0}=\cup \Pi _{n}^{0}$
(Cohen forcing); and the existence of minimal covers for Turing reducibility (as mentioned in [Reference Shore27, p. 395]; Sacks forcing).
$\Pi _{\infty }^{0}=\cup \Pi _{n}^{0}$
(Cohen forcing); and the existence of minimal covers for Turing reducibility (as mentioned in [Reference Shore27, p. 395]; Sacks forcing).
Remark 4.14. Moving outside of et-forcings, we can, for example, extend the G-
![]() $\Pi _{1}^{1}$
conservation results from RCA
$\Pi _{1}^{1}$
conservation results from RCA
![]() $_{0}$
to WKL
$_{0}$
to WKL
![]() $_{0}$
as WKL is a
$_{0}$
as WKL is a
![]() $\Pi _{2}^{1}$
principle for which solutions can be provided by forcing (Harrington; see [Reference Simpson28, Section IX.2]). So, in particular, if solutions to a
$\Pi _{2}^{1}$
principle for which solutions can be provided by forcing (Harrington; see [Reference Simpson28, Section IX.2]). So, in particular, if solutions to a
![]() $\Pi _{2}^{1}$
principle Q can be provided by forcing, then
$\Pi _{2}^{1}$
principle Q can be provided by forcing, then
![]() $ Q+WKL_{0}\nvdash ACA_{0}$
as ACA
$ Q+WKL_{0}\nvdash ACA_{0}$
as ACA
![]() $_{0}$
is not
$_{0}$
is not
![]() $\Pi _{1}^{1}$
conservative over RCA
$\Pi _{1}^{1}$
conservative over RCA
![]() $_{0}$
. (Indeed, [Reference Simpson28, Corollary VIII.1.8] shows that ACA
$_{0}$
. (Indeed, [Reference Simpson28, Corollary VIII.1.8] shows that ACA
![]() $_{0}$
is not conservative over RCA
$_{0}$
is not conservative over RCA
![]() $_{0}$
even for
$_{0}$
even for
![]() $\Pi _{1}^{0}$
sentences.) Note that as WKL is itself an r-
$\Pi _{1}^{0}$
sentences.) Note that as WKL is itself an r-
![]() $\Pi _{2}^{1}$
formula, it is not r-
$\Pi _{2}^{1}$
formula, it is not r-
![]() $\Pi _{2}^{1} $
conservative over RCA
$\Pi _{2}^{1} $
conservative over RCA
![]() $_{0}$
and so solutions for it cannot be produced by et-forcings. (They are, however, produced in the usual proof by tree forcings, just not effective ones.)
$_{0}$
and so solutions for it cannot be produced by et-forcings. (They are, however, produced in the usual proof by tree forcings, just not effective ones.)
The proof in [Reference Simpson28, Corollary VIII.1.8] is an application of Gödel’s second incompleteness theorem. A semantic and more dramatic demonstration that, in this setting,
![]() $Q+WKL_{0}\nvdash ACA_{0}$
is provided by Theorem 4.5.3 when solutions for Q can be provided by cone avoiding forcings: If
$Q+WKL_{0}\nvdash ACA_{0}$
is provided by Theorem 4.5.3 when solutions for Q can be provided by cone avoiding forcings: If
![]() $\mathcal {N}$
is a model of RCA
$\mathcal {N}$
is a model of RCA
![]() $_{0}$
but not ACA
$_{0}$
but not ACA
![]() $_{0}$
, i.e., there is an
$_{0}$
, i.e., there is an
![]() $X\in S(\mathcal {N)}$
such that there is no
$X\in S(\mathcal {N)}$
such that there is no
![]() $Y\in S(\mathcal {N})$
satisfying the definition of
$Y\in S(\mathcal {N})$
satisfying the definition of
![]() $X^{\prime }$
then there is an extension
$X^{\prime }$
then there is an extension
![]() $\mathcal {N} ^{\prime }$
of
$\mathcal {N} ^{\prime }$
of
![]() $\mathcal {N}$
with the same first order part which also has no such Y. Indeed, we can even omit every subset of N which is definable over
$\mathcal {N}$
with the same first order part which also has no such Y. Indeed, we can even omit every subset of N which is definable over
![]() $\mathcal {N}$
but not in
$\mathcal {N}$
but not in
![]() $S(\mathcal {N})$
. These remarks also apply when we add on WKL as the forcing that provides solutions for it has the cone avoiding property by using the standard arguments for cone avoiding for
$S(\mathcal {N})$
. These remarks also apply when we add on WKL as the forcing that provides solutions for it has the cone avoiding property by using the standard arguments for cone avoiding for
![]() $\Pi _{1}^{0}$
forcing in recursion theory [Reference Jockusch and Soare16].
$\Pi _{1}^{0}$
forcing in recursion theory [Reference Jockusch and Soare16].
We would like to apply all these results to the principles LF
![]() $_{XY}$
of Definition 3.5 as well as others to show that they do not imply ACA
$_{XY}$
of Definition 3.5 as well as others to show that they do not imply ACA
![]() $ _{0}$
and indeed are highly conservative over RCA
$ _{0}$
and indeed are highly conservative over RCA
![]() $_{0}$
. As we already showed that each LF
$_{0}$
. As we already showed that each LF
![]() $_{XY}$
becomes a THA when added to ACA
$_{XY}$
becomes a THA when added to ACA
![]() $_{0}$
, this will show that all of them (even when combined with each other as well as WKL, COH, and more) are ATHAs. Our plan is to first show that they all have solutions provided by et-forcings. The problem will then be that they are not
$_{0}$
, this will show that all of them (even when combined with each other as well as WKL, COH, and more) are ATHAs. Our plan is to first show that they all have solutions provided by et-forcings. The problem will then be that they are not
![]() $\Pi _{2}^{1}$
principles and so we will also have to extend the theorems above to a larger class of principles.
$\Pi _{2}^{1}$
principles and so we will also have to extend the theorems above to a larger class of principles.
5 Extending the class of principles
We want to prove that the principles asserted to be ATHAs in Section 3 do not imply ACA
![]() $_{0}$
by showing that solutions can be provided by et-forcings and that we can extend the conservation/preservation results of Section 4 to a wider class of principles than
$_{0}$
by showing that solutions can be provided by et-forcings and that we can extend the conservation/preservation results of Section 4 to a wider class of principles than
![]() $\Pi _{2}^{1}$
that include all of the ones that we claimed to be ATHAs and more. We begin with showing how solutions for all of them can be provided by et-forcings. The most interesting ones are the ones about finding locally finite subgraphs with various properties that began our study of ATHAs: LF
$\Pi _{2}^{1}$
that include all of the ones that we claimed to be ATHAs and more. We begin with showing how solutions for all of them can be provided by et-forcings. The most interesting ones are the ones about finding locally finite subgraphs with various properties that began our study of ATHAs: LF
![]() $_{XY}$
.
$_{XY}$
.
Theorem 5.1. Given an X-graph H in a countable
![]() $\mathcal {N}\vDash RCA_{0}$
which contains arbitrarily many Y-disjoint rays we can define an et-forcing
$\mathcal {N}\vDash RCA_{0}$
which contains arbitrarily many Y-disjoint rays we can define an et-forcing
![]() $\mathcal {P}$
and a countable collection of dense sets
$\mathcal {P}$
and a countable collection of dense sets
![]() $\mathcal {D }$
such that any
$\mathcal {D }$
such that any
![]() $\mathcal {D}$
-generic G provides a locally finite X-subgraph
$\mathcal {D}$
-generic G provides a locally finite X-subgraph
![]() $H^{\prime }$
of H which also contains arbitrarily many Y-disjoint rays.
$H^{\prime }$
of H which also contains arbitrarily many Y-disjoint rays.
Proof The set of vertices of
![]() $H^{\prime }$
is just that of H which, without loss of generality, we may take to be N. Thus we only need to specify the edges of
$H^{\prime }$
is just that of H which, without loss of generality, we may take to be N. Thus we only need to specify the edges of
![]() $H^{\prime }$
. We use a pairing function to view the numbers n as all possible edges. We write
$H^{\prime }$
. We use a pairing function to view the numbers n as all possible edges. We write
![]() $M(v,n)$
to mean that the vertex v is an element of the edge n.
$M(v,n)$
to mean that the vertex v is an element of the edge n.
Our conditions
![]() $\left \langle \tau ,T\right \rangle $
will satisfy various requirements in addition to the ones common to all et-forcings. The first is that, the trees are binary (i.e., subsets of
$\left \langle \tau ,T\right \rangle $
will satisfy various requirements in addition to the ones common to all et-forcings. The first is that, the trees are binary (i.e., subsets of
![]() $2^{<N}$
) and for any
$2^{<N}$
) and for any
![]() $\sigma \in T$
, if (the pair) n is not an edge in H then
$\sigma \in T$
, if (the pair) n is not an edge in H then
![]() $\sigma (n)=0$
. Thus each generic
$\sigma (n)=0$
. Thus each generic
![]() $G:N\mathbb {\rightarrow }N$
can be seen as a subgraph of H in
$G:N\mathbb {\rightarrow }N$
can be seen as a subgraph of H in
![]() $\mathcal {N}[G]$
. (G supplies the characteristic function of the set of edges. The set of vertices we have already set to be N.)
$\mathcal {N}[G]$
. (G supplies the characteristic function of the set of edges. The set of vertices we have already set to be N.)
The intuition behind the rest of the definition of the notion of forcing is that we want to be able, on one hand, to specify that the set of edges from some sequence of disjoint rays of length m can be added to the final graph. On the other, for an arbitrary vertex v we want to be able to specify that no additional edges containing v can be added to the graph and to guarantee that only finitely many of the edges already guaranteed to be in the graph have v as a vertex.
To these ends, for each potential condition
![]() $\left \langle \tau ,T\right \rangle $
we first specify various sets of edges n based on what the condition says about their membership in G. First we have the
$\left \langle \tau ,T\right \rangle $
we first specify various sets of edges n based on what the condition says about their membership in G. First we have the
![]() $n>|\tau |$
such that all branches G in T have
$n>|\tau |$
such that all branches G in T have
![]() $G(n)=1$
. We denote the set of such n as
$G(n)=1$
. We denote the set of such n as
![]() $Y^{\left \langle \tau ,T\right \rangle }=\{n>|\tau ||(\forall \sigma \in T)(\sigma (n)=1)\}$
. Next we have the ones with
$Y^{\left \langle \tau ,T\right \rangle }=\{n>|\tau ||(\forall \sigma \in T)(\sigma (n)=1)\}$
. Next we have the ones with
![]() $G(n)=0$
for all
$G(n)=0$
for all
![]() $ G$
on T,
$ G$
on T,
![]() $N^{\left \langle \tau ,T\right \rangle }=\{n>|\tau ||(\forall \sigma \in T)(\sigma (n)=0)\}$
. Finally, we have the n at which G can go either way,
$N^{\left \langle \tau ,T\right \rangle }=\{n>|\tau ||(\forall \sigma \in T)(\sigma (n)=0)\}$
. Finally, we have the n at which G can go either way,
![]() . Note that as T is binary all these sets are in
. Note that as T is binary all these sets are in
![]() $ \mathcal {N}$
(even uniformly in
$ \mathcal {N}$
(even uniformly in
![]() $\left \langle \tau ,T\right \rangle $
). We require that every
$\left \langle \tau ,T\right \rangle $
). We require that every
![]() $n>|\tau |$
is in one of these (clearly disjoint) sets.
$n>|\tau |$
is in one of these (clearly disjoint) sets.
We also impose some requirements on the nature of the first two of these three sets. For
![]() $Y^{\left \langle \tau ,T\right \rangle }$
there is a function
$Y^{\left \langle \tau ,T\right \rangle }$
there is a function
![]() $f_{\left \langle \tau ,T\right \rangle }=f$
such that
$f_{\left \langle \tau ,T\right \rangle }=f$
such that
![]() $\forall v(f(v)=|\{n\in Y^{\left \langle \tau ,T\right \rangle }|M(v,n)\}|)$
. So not only are there only finitely many
$\forall v(f(v)=|\{n\in Y^{\left \langle \tau ,T\right \rangle }|M(v,n)\}|)$
. So not only are there only finitely many
![]() $n\in Y^{\left \langle \tau ,T\right \rangle }$
such that
$n\in Y^{\left \langle \tau ,T\right \rangle }$
such that
![]() $ v $
is a member of the edge n but we know how many and so we can uniformly determine which they are. Finally, for
$ v $
is a member of the edge n but we know how many and so we can uniformly determine which they are. Finally, for
![]() $N^{\left \langle \tau ,T\right \rangle }$
there is a finite set
$N^{\left \langle \tau ,T\right \rangle }$
there is a finite set
![]() $A_{\left \langle \tau ,T\right \rangle }=A$
such that
$A_{\left \langle \tau ,T\right \rangle }=A$
such that
![]() $(\forall n\in N^{\left \langle \tau ,T\right \rangle })(\exists v\in A)M(n,v)$
and
$(\forall n\in N^{\left \langle \tau ,T\right \rangle })(\exists v\in A)M(n,v)$
and
![]() $(\forall n>|\tau |)(\forall v\in A)(M(n,v)\rightarrow n\notin U^{\left \langle \tau ,T\right \rangle })$
. We call such f and A witnesses that a
$(\forall n>|\tau |)(\forall v\in A)(M(n,v)\rightarrow n\notin U^{\left \langle \tau ,T\right \rangle })$
. We call such f and A witnesses that a
![]() $\left \langle \tau ,T\right \rangle $
satisfying the other requirements on
$\left \langle \tau ,T\right \rangle $
satisfying the other requirements on
![]() $Y^{\left \langle \tau ,T\right \rangle }$
,
$Y^{\left \langle \tau ,T\right \rangle }$
,
![]() $N^{\left \langle \tau ,T\right \rangle }$
and
$N^{\left \langle \tau ,T\right \rangle }$
and
![]() $U^{\left \langle \tau ,T\right \rangle }$
is a condition. Note that f is uniquely determined but A need not be.
$U^{\left \langle \tau ,T\right \rangle }$
is a condition. Note that f is uniquely determined but A need not be.
Given this set of conditions, the forcing partial order is just the one defined by the basic requirement for et-forcings in Definition 4.1.2.
Note that if
![]() $\left \langle \tau ,T\right \rangle $
is a condition with witnesses f and A and
$\left \langle \tau ,T\right \rangle $
is a condition with witnesses f and A and
![]() $\sigma \in T$
with
$\sigma \in T$
with
![]() $|\sigma |>|\tau |$
then
$|\sigma |>|\tau |$
then
![]() $ \left \langle \sigma ,T^{\sigma }\right \rangle $
(as defined in Notation 4.3) is also a condition with the same A and a slightly modified
$ \left \langle \sigma ,T^{\sigma }\right \rangle $
(as defined in Notation 4.3) is also a condition with the same A and a slightly modified
![]() $ f^{\prime }$
as witnesses: let
$ f^{\prime }$
as witnesses: let
![]() $f^{\prime }(v)=f(v)-|\{n\in Y^{\left \langle \tau ,T\right \rangle }|~|\tau |\leq n<|\sigma |~\wedge M(v,n)\}|$
. Thus we have defined an et-forcing.
$f^{\prime }(v)=f(v)-|\{n\in Y^{\left \langle \tau ,T\right \rangle }|~|\tau |\leq n<|\sigma |~\wedge M(v,n)\}|$
. Thus we have defined an et-forcing.
We now argue that we can describe a collection
![]() $\mathcal {D}$
of dense sets that guarantee that any
$\mathcal {D}$
of dense sets that guarantee that any
![]() $\mathcal {D}$
-generic G determines (as described above) a locally finite subgraph
$\mathcal {D}$
-generic G determines (as described above) a locally finite subgraph
![]() $H^{\prime }$
of H which contains arbitrarily many disjoint rays.
$H^{\prime }$
of H which contains arbitrarily many disjoint rays.
First, we claim that for each vertex v and condition
![]() $\left \langle \tau ,T\right \rangle $
with witnesses A and f as above there is a
$\left \langle \tau ,T\right \rangle $
with witnesses A and f as above there is a
![]() $ \left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
with witnesses
$ \left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
with witnesses
![]() $f^{\prime }$
and
$f^{\prime }$
and
![]() $A^{\prime }$
such that
$A^{\prime }$
such that
![]() $ v\in A^{\prime }$
. In fact, it is easy to see from the definition of the allowed conditions that for any
$ v\in A^{\prime }$
. In fact, it is easy to see from the definition of the allowed conditions that for any
![]() $v\notin A_{\left \langle \tau ,T\right \rangle }$
, there is a
$v\notin A_{\left \langle \tau ,T\right \rangle }$
, there is a
![]() $T^{\prime }\subseteq T$
such that
$T^{\prime }\subseteq T$
such that
![]() $ \left \langle \tau ,T^{\prime }\right \rangle $
is a condition with witness f and
$ \left \langle \tau ,T^{\prime }\right \rangle $
is a condition with witness f and
![]() $A^{\prime }=A\cup \{v\}$
. We refine T by removing any
$A^{\prime }=A\cup \{v\}$
. We refine T by removing any
![]() $\sigma \supset \tau $
such that there is an
$\sigma \supset \tau $
such that there is an
![]() $n\geq |\tau |$
which is an edge containing v as a vertex such that both
$n\geq |\tau |$
which is an edge containing v as a vertex such that both
![]() and
and
![]() are in T and
are in T and
![]() $\sigma (n)=1$
. This moves n from
$\sigma (n)=1$
. This moves n from
![]() $U^{\left \langle \tau ,T\right \rangle }$
to
$U^{\left \langle \tau ,T\right \rangle }$
to
![]() $N^{\left \langle \tau ,T\right \rangle }$
and so does not affect the calculation of the required f.
$N^{\left \langle \tau ,T\right \rangle }$
and so does not affect the calculation of the required f.
So, by genericity (for these dense sets), for any vertex v there is a condition
![]() $\left \langle \tau ,T\right \rangle $
in the generic filter such that it has a witness
$\left \langle \tau ,T\right \rangle $
in the generic filter such that it has a witness
![]() $A_{\left \langle \tau ,T\right \rangle }$
containing v .
$A_{\left \langle \tau ,T\right \rangle }$
containing v .
As for this enforcing local finiteness, consider any condition
![]() $\left \langle \tau ,T\right \rangle $
with witnesses such that
$\left \langle \tau ,T\right \rangle $
with witnesses such that
![]() $v\in A_{\left \langle \tau ,T\right \rangle }$
. We claim that for any G on T there are only finitely many n with
$v\in A_{\left \langle \tau ,T\right \rangle }$
. We claim that for any G on T there are only finitely many n with
![]() $G(n)=1$
and
$G(n)=1$
and
![]() $M(v,n)$
. Of course, there are at most
$M(v,n)$
. Of course, there are at most
![]() $|\tau |$
many edges
$|\tau |$
many edges
![]() $n<|\tau |$
such that
$n<|\tau |$
such that
![]() $M(v,n)$
. There are only
$M(v,n)$
. There are only
![]() $f(v)$
many
$f(v)$
many
![]() $n\in Y^{\left \langle \tau ,T\right \rangle }=Y^{\left \langle \tau ,T^{\prime }\right \rangle }$
such that
$n\in Y^{\left \langle \tau ,T\right \rangle }=Y^{\left \langle \tau ,T^{\prime }\right \rangle }$
such that
![]() $M(v,n)$
and by our second condition about
$M(v,n)$
and by our second condition about
![]() $v\in A$
there are no
$v\in A$
there are no
![]() $n\in U^{\left \langle \tau ,T\right \rangle }$
such that
$n\in U^{\left \langle \tau ,T\right \rangle }$
such that
![]() $ M(v,n)$
. Of course, there are no
$ M(v,n)$
. Of course, there are no
![]() $n\in N^{\left \langle \tau ,T^{\prime }\right \rangle }$
such that
$n\in N^{\left \langle \tau ,T^{\prime }\right \rangle }$
such that
![]() $G(n)=1$
. (We have, in fact, uniformly over all
$G(n)=1$
. (We have, in fact, uniformly over all
![]() $ G$
on T calculated the number of n such that
$ G$
on T calculated the number of n such that
![]() $M(v,n)$
.)
$M(v,n)$
.)
Finally, we show that for each
![]() $m\in N$
and condition
$m\in N$
and condition
![]() $\left \langle \tau ,T\right \rangle $
with witnesses as above, there is an extension
$\left \langle \tau ,T\right \rangle $
with witnesses as above, there is an extension
![]() $ \left \langle \tau ,T^{\prime }\right \rangle $
such that for any G on
$ \left \langle \tau ,T^{\prime }\right \rangle $
such that for any G on
![]() $ \left \langle \tau ,T^{\prime }\right \rangle $
the associated graph contains
$ \left \langle \tau ,T^{\prime }\right \rangle $
the associated graph contains
![]() $ m$
many disjoint rays.
$ m$
many disjoint rays.
By assumption there is a sequence
![]() $\left \langle V_{i},E_{i},f_{i}\right \rangle _{i<m+|\tau |}$
of disjoint rays in H. Obviously, there are at most
$\left \langle V_{i},E_{i},f_{i}\right \rangle _{i<m+|\tau |}$
of disjoint rays in H. Obviously, there are at most
![]() $|\tau |$
many n such that
$|\tau |$
many n such that
![]() $\tau (n)=0$
. As each edge n can appear in at most one
$\tau (n)=0$
. As each edge n can appear in at most one
![]() $E_{i}$
we can thin out the given sequence to one
$E_{i}$
we can thin out the given sequence to one
![]() $\left \langle V_{i}^{\prime },E_{i}^{\prime },f_{i}^{\prime }\right \rangle _{i<m}$
of disjoint rays none of which contains an edge n for which
$\left \langle V_{i}^{\prime },E_{i}^{\prime },f_{i}^{\prime }\right \rangle _{i<m}$
of disjoint rays none of which contains an edge n for which
![]() $\tau (n)=0$
.
$\tau (n)=0$
.
Next we deal with the conditions imposed by
![]() $A_{\left \langle \tau ,T\right \rangle }$
. For each
$A_{\left \langle \tau ,T\right \rangle }$
. For each
![]() $i<m$
we let
$i<m$
we let
![]() $g(i)=0$
if no
$g(i)=0$
if no
![]() $v\in A_{\left \langle \tau ,T\right \rangle }$
is in
$v\in A_{\left \langle \tau ,T\right \rangle }$
is in
![]() $V_{i}^{\prime }$
. Otherwise we let
$V_{i}^{\prime }$
. Otherwise we let
![]() $g(i)=\max \{n|f_{i}^{\prime }(n)\in A_{\left \langle \tau ,T\right \rangle }$
and
$g(i)=\max \{n|f_{i}^{\prime }(n)\in A_{\left \langle \tau ,T\right \rangle }$
and
![]() $f_{i}^{\prime }(n)\in V_{i}^{\prime }\}+1$
. Our construction so far guarantees that
$f_{i}^{\prime }(n)\in V_{i}^{\prime }\}+1$
. Our construction so far guarantees that
![]() $g:m\rightarrow N$
is a member of
$g:m\rightarrow N$
is a member of
![]() $ \mathcal {N}$
. Thus we can thin out
$ \mathcal {N}$
. Thus we can thin out
![]() $\left \langle V_{i}^{\prime },E_{i}^{\prime },f_{i}^{\prime }\right \rangle _{i<m}$
by taking the tail of each
$\left \langle V_{i}^{\prime },E_{i}^{\prime },f_{i}^{\prime }\right \rangle _{i<m}$
by taking the tail of each
![]() $V_{i}^{\prime }$
beyond
$V_{i}^{\prime }$
beyond
![]() $g(i)$
to get
$g(i)$
to get
![]() $V_{i}^{\prime \prime }=V_{i}^{\prime }-\{f_{i}^{\prime }(n)|n<g(i)\}$
,
$V_{i}^{\prime \prime }=V_{i}^{\prime }-\{f_{i}^{\prime }(n)|n<g(i)\}$
,
![]() $E_{i}^{\prime \prime }=E_{i}^{\prime }-\{\left \langle f_{i}^{\prime }(n),f_{i}^{\prime }(n+1)\right \rangle |n<g(i)\}$
, and
$E_{i}^{\prime \prime }=E_{i}^{\prime }-\{\left \langle f_{i}^{\prime }(n),f_{i}^{\prime }(n+1)\right \rangle |n<g(i)\}$
, and
![]() $f_{i}^{\prime \prime }(n)=f_{i}^{\prime }(n+g(i))$
. Let
$f_{i}^{\prime \prime }(n)=f_{i}^{\prime }(n+g(i))$
. Let
![]() $E^{\prime \prime }=\cup \{E_{i}^{\prime \prime }|i<m\}$
. This sequence clearly provides m many disjoint rays in H. Thus (by genericity) it suffices to define a condition
$E^{\prime \prime }=\cup \{E_{i}^{\prime \prime }|i<m\}$
. This sequence clearly provides m many disjoint rays in H. Thus (by genericity) it suffices to define a condition
![]() $\left \langle \tau ,T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
such that
$\left \langle \tau ,T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
such that
![]() $E^{\prime \prime }\subseteq Y^{\left \langle \tau ,T^{\prime }\right \rangle }$
as then for any G on
$E^{\prime \prime }\subseteq Y^{\left \langle \tau ,T^{\prime }\right \rangle }$
as then for any G on
![]() $\left \langle \tau ,T^{\prime }\right \rangle $
,
$\left \langle \tau ,T^{\prime }\right \rangle $
,
![]() $G(n)=1$
for all the edges
$G(n)=1$
for all the edges
![]() $n\in \ E_{i}^{\prime \prime }$
for every
$n\in \ E_{i}^{\prime \prime }$
for every
![]() $i<m$
and so
$i<m$
and so
![]() $ \left \langle V_{i}^{\prime \prime },E_{i}^{\prime \prime },f_{i}^{\prime \prime }\right \rangle _{i<m}$
shows in
$ \left \langle V_{i}^{\prime \prime },E_{i}^{\prime \prime },f_{i}^{\prime \prime }\right \rangle _{i<m}$
shows in
![]() $\mathcal {N}[G]$
that the subgraph
$\mathcal {N}[G]$
that the subgraph
![]() $ H^{\prime }$
of H associated with G has m many disjoint rays.
$ H^{\prime }$
of H associated with G has m many disjoint rays.
The crucial point is that we have designed
![]() $\left \langle V_{i}^{\prime \prime },E_{i}^{^{\prime \prime }},f_{i}^{\prime \prime }\right \rangle _{i<m} $
so that
$\left \langle V_{i}^{\prime \prime },E_{i}^{^{\prime \prime }},f_{i}^{\prime \prime }\right \rangle _{i<m} $
so that
![]() $E^{\prime \prime }\cap N^{\left \langle \tau ,T\right \rangle }=\emptyset $
. Thus we may define a tree
$E^{\prime \prime }\cap N^{\left \langle \tau ,T\right \rangle }=\emptyset $
. Thus we may define a tree
![]() $T^{\prime }\subseteq T$
by simply removing all
$T^{\prime }\subseteq T$
by simply removing all
![]() $\sigma $
such that
$\sigma $
such that
![]() $\sigma (n)=0$
for some
$\sigma (n)=0$
for some
![]() $n\in E^{\prime \prime }$
. This change at most moves some edges
$n\in E^{\prime \prime }$
. This change at most moves some edges
![]() $n\in U^{\left \langle \tau ,T\right \rangle }$
to
$n\in U^{\left \langle \tau ,T\right \rangle }$
to
![]() $Y^{\left \langle \tau ,T^{\prime }\right \rangle }$
and makes
$Y^{\left \langle \tau ,T^{\prime }\right \rangle }$
and makes
![]() $Y^{\left \langle \tau ,T^{\prime }\right \rangle }=Y=Y^{\left \langle \tau ,T\right \rangle }\cup E^{\prime \prime }$
as desired while keeping
$Y^{\left \langle \tau ,T^{\prime }\right \rangle }=Y=Y^{\left \langle \tau ,T\right \rangle }\cup E^{\prime \prime }$
as desired while keeping
![]() $N^{\left \langle \tau ,T^{\prime }\right \rangle }=N^{\left \langle \tau ,T\right \rangle }$
. If
$N^{\left \langle \tau ,T^{\prime }\right \rangle }=N^{\left \langle \tau ,T\right \rangle }$
. If
![]() $\left \langle \tau ,T^{\prime }\right \rangle $
is a condition, it clearly extends
$\left \langle \tau ,T^{\prime }\right \rangle $
is a condition, it clearly extends
![]() $\left \langle \tau ,T\right \rangle $
and so we only have to verify that it is one. As we already have the required facts about
$\left \langle \tau ,T\right \rangle $
and so we only have to verify that it is one. As we already have the required facts about
![]() $Y^{\left \langle \tau ,T^{\prime }\right \rangle }$
,
$Y^{\left \langle \tau ,T^{\prime }\right \rangle }$
,
![]() $N^{\left \langle \tau ,T\right \rangle }$
, and
$N^{\left \langle \tau ,T\right \rangle }$
, and
![]() $ U^{\left \langle \tau ,T^{\prime }\right \rangle } $
, we only need to supply witnesses
$ U^{\left \langle \tau ,T^{\prime }\right \rangle } $
, we only need to supply witnesses
![]() $f^{\prime }$
and
$f^{\prime }$
and
![]() $A^{\prime }$
. As we have the witness f for
$A^{\prime }$
. As we have the witness f for
![]() $ \left \langle \tau ,T\right \rangle $
, to get
$ \left \langle \tau ,T\right \rangle $
, to get
![]() $f^{\prime }$
it clearly suffices to compute for each v the number of
$f^{\prime }$
it clearly suffices to compute for each v the number of
![]() $n>|\tau |$
such that
$n>|\tau |$
such that
![]() $n\in E^{\prime \prime }-Y^{\left \langle \tau ,T\right \rangle }$
and
$n\in E^{\prime \prime }-Y^{\left \langle \tau ,T\right \rangle }$
and
![]() $M(v,n)$
. We begin with the sequence
$M(v,n)$
. We begin with the sequence
![]() $\left \langle V_{i}^{\prime \prime },E_{i}^{^{\prime \prime }},f_{i}^{\prime \prime }\right \rangle _{i<m}$
of disjoint rays such that
$\left \langle V_{i}^{\prime \prime },E_{i}^{^{\prime \prime }},f_{i}^{\prime \prime }\right \rangle _{i<m}$
of disjoint rays such that
![]() $E^{\prime \prime }=\cup \{E_{i}^{^{\prime \prime }}|i<m\}$
. We first determine those i for which
$E^{\prime \prime }=\cup \{E_{i}^{^{\prime \prime }}|i<m\}$
. We first determine those i for which
![]() $v\in V_{i}^{\prime \prime }$
. (For the other
$v\in V_{i}^{\prime \prime }$
. (For the other
![]() $ j$
there are no
$ j$
there are no
![]() $n\in E_{j}^{\prime \prime }$
with
$n\in E_{j}^{\prime \prime }$
with
![]() $M(v,n)$
.) As v appears in each of these
$M(v,n)$
.) As v appears in each of these
![]() $V_{i}^{\prime \prime }$
only once, there are at most two such edges in each of these
$V_{i}^{\prime \prime }$
only once, there are at most two such edges in each of these
![]() $E_{i}^{\prime \prime }$
. Using this information we can determine for which edges
$E_{i}^{\prime \prime }$
. Using this information we can determine for which edges
![]() $n\in E_{i}^{^{\prime \prime }}-Y^{\left \langle \tau ,T\right \rangle }$
we have
$n\in E_{i}^{^{\prime \prime }}-Y^{\left \langle \tau ,T\right \rangle }$
we have
![]() $M(v,n).$
As the
$M(v,n).$
As the
![]() $ E_{i}^{\prime \prime }$
are disjoint, we can now simply add up the contributions (of one or two) from each
$ E_{i}^{\prime \prime }$
are disjoint, we can now simply add up the contributions (of one or two) from each
![]() $E_{i}^{\prime \prime }-Y^{\left \langle \tau ,T\right \rangle }$
with
$E_{i}^{\prime \prime }-Y^{\left \langle \tau ,T\right \rangle }$
with
![]() $v\in V_{i}^{\prime \prime }$
to get the amount we need to add to
$v\in V_{i}^{\prime \prime }$
to get the amount we need to add to
![]() $f(v)$
to get the desired
$f(v)$
to get the desired
![]() $f^{\prime }(v)$
. Finally, as
$f^{\prime }(v)$
. Finally, as
![]() $N^{\left \langle \tau ,T\right \rangle }=N^{\left \langle \tau ,T^{\prime }\right \rangle }$
and
$N^{\left \langle \tau ,T\right \rangle }=N^{\left \langle \tau ,T^{\prime }\right \rangle }$
and
![]() $U^{\left \langle \tau ,T^{\prime }\right \rangle }\subseteq U^{\left \langle \tau ,T\right \rangle }$
, we can take the witness A for
$U^{\left \langle \tau ,T^{\prime }\right \rangle }\subseteq U^{\left \langle \tau ,T\right \rangle }$
, we can take the witness A for
![]() $\left \langle \tau ,T\right \rangle $
to also be the desired witness
$\left \langle \tau ,T\right \rangle $
to also be the desired witness
![]() $A^{\prime }$
for
$A^{\prime }$
for
![]() $\left \langle \tau ,T^{\prime }\right \rangle $
.
$\left \langle \tau ,T^{\prime }\right \rangle $
.
So solutions to all the LF principles can be provided by et-forcings. We would like to draw the conclusions that give the conservation and preservation results of Theorems 4.11–4.13 for all the LF principles. The problem is that they are not
![]() $\Pi _{2}^{1}$
-principles. We actually needed two properties of principles to get the applications we proved for
$\Pi _{2}^{1}$
-principles. We actually needed two properties of principles to get the applications we proved for
![]() $\Pi _{2}^{1}$
principles.
$\Pi _{2}^{1}$
principles.
One was that once a solution was provided in
![]() $\mathcal {N}[G]$
by forcing, it remained a solution in each later extension and so at the end. This was immediate from the fact that the properties of interest were arithmetic and that the extensions preserved the first order part of the model. This property still holds for the conclusions of the LF principles as the conditions required of the constructed subgraph
$\mathcal {N}[G]$
by forcing, it remained a solution in each later extension and so at the end. This was immediate from the fact that the properties of interest were arithmetic and that the extensions preserved the first order part of the model. This property still holds for the conclusions of the LF principles as the conditions required of the constructed subgraph
![]() $H^{\prime }$
(local finiteness) and the finite sequences
$H^{\prime }$
(local finiteness) and the finite sequences
![]() $\left \langle V_{i},E_{i},f_{i}\right \rangle _{i<m}$
(they are finite sequences of rays) are also arithmetic.
$\left \langle V_{i},E_{i},f_{i}\right \rangle _{i<m}$
(they are finite sequences of rays) are also arithmetic.
The other property was that every instance of the problem that is in the final limit model already appears in one of the models along the way. (This allows us to handle all the instances that there are at end as we go along.) This property is not obvious for the LF principles as the condition for H to be an instance is that H is a graph that contains arbitrarily many rays and so of the form
![]() $\forall m\exists W(\left \langle W^{[i]}|i<m\right \rangle $
is a sequence of m many disjoint rays in H). It could be that for some graph H constructed along the way the required Ws for each
$\forall m\exists W(\left \langle W^{[i]}|i<m\right \rangle $
is a sequence of m many disjoint rays in H). It could be that for some graph H constructed along the way the required Ws for each
![]() $m\in N$
get constructed cofinally in the sequence of extensions and so are instances in the limit model never solved along the way. (There are special situations for which this cannot happen. One, in particular, is that the failure of X to be an instance is equivalent to some trees T in the model with H do not have branches in the model. Examples of this situation is TAC and its variants in Proposition 5.13 and Definition 5.15. As et-forcings preserve this fact, H would not be an instance in the limit stage model.) Here we provide a simpler more generally applicable solution: extend the iteration to
$m\in N$
get constructed cofinally in the sequence of extensions and so are instances in the limit model never solved along the way. (There are special situations for which this cannot happen. One, in particular, is that the failure of X to be an instance is equivalent to some trees T in the model with H do not have branches in the model. Examples of this situation is TAC and its variants in Proposition 5.13 and Definition 5.15. As et-forcings preserve this fact, H would not be an instance in the limit stage model.) Here we provide a simpler more generally applicable solution: extend the iteration to
![]() $\omega _{1}$
. (One can also get by with a countable iteration albeit longer than
$\omega _{1}$
. (One can also get by with a countable iteration albeit longer than
![]() $\omega $
by a look ahead procedure to make sure possible instances with parameters that we have now but witnesses that may occur later are handled now. The
$\omega $
by a look ahead procedure to make sure possible instances with parameters that we have now but witnesses that may occur later are handled now. The
![]() $\omega _{1}$
iteration is, however, simpler and useful later.)
$\omega _{1}$
iteration is, however, simpler and useful later.)
Theorem 5.2. Each of the LF
![]() $_{XY}$
principles is G-r-
$_{XY}$
principles is G-r-
![]() $\Pi _{2}^{1}$
(and so G-r-
$\Pi _{2}^{1}$
(and so G-r-
![]() $\Pi _{1}^{1}$
) conservative over RCA
$\Pi _{1}^{1}$
) conservative over RCA
![]() $_{0}$
. Moreover, they can be realized in extensions that omit branches (and so avoid cones) as in Theorem 4.13.
$_{0}$
. Moreover, they can be realized in extensions that omit branches (and so avoid cones) as in Theorem 4.13.
Proof Continue the iteration by the et-forcings that provide solutions to an instance of one of the LF
![]() $_{XY}$
principles through
$_{XY}$
principles through
![]() $\omega _{1}$
many steps in such a way that every H that appears as an instance at any
$\omega _{1}$
many steps in such a way that every H that appears as an instance at any
![]() $ \mathcal {N}_{\alpha }$
gets a solution in some
$ \mathcal {N}_{\alpha }$
gets a solution in some
![]() $\mathcal {N}_{\beta +1}$
for
$\mathcal {N}_{\beta +1}$
for
![]() $ \beta \geq \alpha $
. At limit levels we still act continuously:
$ \beta \geq \alpha $
. At limit levels we still act continuously:
![]() $\mathcal {N} _{\lambda }$
is the union of the
$\mathcal {N} _{\lambda }$
is the union of the
![]() $\mathcal {N}_{\alpha }$
for
$\mathcal {N}_{\alpha }$
for
![]() $\alpha <\lambda $
. Now if
$\alpha <\lambda $
. Now if
![]() $H\in \mathcal {N}_{\omega _{1}}$
is an instance of the LF
$H\in \mathcal {N}_{\omega _{1}}$
is an instance of the LF
![]() $ _{XY}$
principle then, not only does H appear in some
$ _{XY}$
principle then, not only does H appear in some
![]() $\mathcal {N} _{\alpha }$
, but so do all the witnesses for H containing m many disjoint rays for every m as there are only countably many
$\mathcal {N} _{\alpha }$
, but so do all the witnesses for H containing m many disjoint rays for every m as there are only countably many
![]() $m\in \mathcal {N }$
and the full sequence is of length
$m\in \mathcal {N }$
and the full sequence is of length
![]() $\omega _{1}$
.
$\omega _{1}$
.
Theorem 5.3. All of the LF
![]() $_{XY}$
principles are ATHAs. Indeed, the conjunction of all of them is an ATHA. Moreover, one can add on all other principles for which solutions can be provided by any of et-forcings mentioned above (Cohen, Laver, Mathias, Sacks, and Silver) while maintaining G-r-
$_{XY}$
principles are ATHAs. Indeed, the conjunction of all of them is an ATHA. Moreover, one can add on all other principles for which solutions can be provided by any of et-forcings mentioned above (Cohen, Laver, Mathias, Sacks, and Silver) while maintaining G-r-
![]() $\Pi _{2}^{1}$
(and so G-r-
$\Pi _{2}^{1}$
(and so G-r-
![]() $\Pi _{1}^{1}$
) conservativity over RCA
$\Pi _{1}^{1}$
) conservativity over RCA
![]() $_{0}$
and realizations by extensions that omit branches (and so avoid cones). One can also add WKL to the theory while maintaining G-r-
$_{0}$
and realizations by extensions that omit branches (and so avoid cones). One can also add WKL to the theory while maintaining G-r-
![]() $\Pi _{1}^{1}$
conservativity and realizations by extensions that avoid cones. Thus even with WKL added the conjunction of all of these principles still do not prove ACA
$\Pi _{1}^{1}$
conservativity and realizations by extensions that avoid cones. Thus even with WKL added the conjunction of all of these principles still do not prove ACA
![]() $_{0}$
and remain an ATHA.
$_{0}$
and remain an ATHA.
Proof Each of these four principles together with ACA
![]() $_{0}$
is a THA by Proposition 3.6. By Theorem 5.2, none of them imply ACA
$_{0}$
is a THA by Proposition 3.6. By Theorem 5.2, none of them imply ACA
![]() $ _{0}$
. Combining them and any other principles for which solutions can be added by et-forcings and even WKL by
$ _{0}$
. Combining them and any other principles for which solutions can be added by et-forcings and even WKL by
![]() $\omega _{1}$
iterations is routine following the route indicated in Remark 4.14 and the comments proceeding it for
$\omega _{1}$
iterations is routine following the route indicated in Remark 4.14 and the comments proceeding it for
![]() $\omega $
length iterations.
$\omega $
length iterations.
We now turn to other examples from the work on Halin type theorems as well as direct variations of choice principles. The guiding idea here is that when a principle calls for a solution which is a sequence
![]() $X_{i}$
of sets each satisfying some property
$X_{i}$
of sets each satisfying some property
![]() $\Psi (i,X)$
we are willing to accept some variations. One is that we accept a sequence
$\Psi (i,X)$
we are willing to accept some variations. One is that we accept a sequence
![]() $Y_{i}$
such that each
$Y_{i}$
such that each
![]() $Y_{i}$
differs from an
$Y_{i}$
differs from an
![]() $X_{i}$
as required by a finite set. The other basic variation is that we allow the desired witnesses to be arbitrarily distributed among the
$X_{i}$
as required by a finite set. The other basic variation is that we allow the desired witnesses to be arbitrarily distributed among the
![]() $Y_{i}$
. That is, for each i there is a j such that
$Y_{i}$
. That is, for each i there is a j such that
![]() $\Psi (i,Y_{j})$
. We designate these modifications of a principle P by
$\Psi (i,Y_{j})$
. We designate these modifications of a principle P by
![]() $P^{\ast }$
and
$P^{\ast }$
and
![]() $P^{-}$
, respectively. Of course, we could also consider allowing both changes: the list contains a finite variant of each
$P^{-}$
, respectively. Of course, we could also consider allowing both changes: the list contains a finite variant of each
![]() $X_{i}$
. The proof of the following implication shows that nothing new appears with this combination.
$X_{i}$
. The proof of the following implication shows that nothing new appears with this combination.
Proposition 5.4 (RCA
 $_{0}$
).
$_{0}$
).
For any principle P whose conclusion asks for a sequence
![]() $ X_{i}$
such that
$ X_{i}$
such that
![]() $\forall i\Psi (i,X_{i})$
,
$\forall i\Psi (i,X_{i})$
,
![]() $P^{\ast }\rightarrow P^{-}$
.
$P^{\ast }\rightarrow P^{-}$
.
Proof Take the solutions
![]() $Y_{i}$
given by
$Y_{i}$
given by
![]() $P^{\ast }$
and construct the sequence
$P^{\ast }$
and construct the sequence
![]() $ Y_{i,\sigma }$
for each finite (binary) string
$ Y_{i,\sigma }$
for each finite (binary) string
![]() $\sigma $
with
$\sigma $
with
![]() $Y_{i,\sigma }(n)=\sigma (n)$
for
$Y_{i,\sigma }(n)=\sigma (n)$
for
![]() $n<|\sigma |$
and
$n<|\sigma |$
and
![]() $Y_{i,\sigma }(n)=Y_{i}(n)$
for
$Y_{i,\sigma }(n)=Y_{i}(n)$
for
![]() $ n\geq |\sigma |$
.
$ n\geq |\sigma |$
.
We begin with a principle from BGS that we examined for locally finite graphs in Proposition 3.3. It extracts the use of
![]() $\Sigma _{1}^{1}$
-AC needed to prove the Halin-type theorems IRT
$\Sigma _{1}^{1}$
-AC needed to prove the Halin-type theorems IRT
![]() $_{XY}$
in ACA
$_{XY}$
in ACA
![]() $_{0}$
as in BGS [Theorem 8.2].
$_{0}$
as in BGS [Theorem 8.2].
Definition 5.5 (SCR
 $_{XY}$
).
$_{XY}$
).
If an X-graph G has arbitrarily many Y -disjoint X-rays then there is a Z such that, for each k,
![]() $Z^{[k]}$
is a sequence
$Z^{[k]}$
is a sequence
![]() $\left \langle Z_{k,i}|1\leq i\leq k\right \rangle $
of pairwise Y -disjoint X-rays in G.
$\left \langle Z_{k,i}|1\leq i\leq k\right \rangle $
of pairwise Y -disjoint X-rays in G.
We note a couple of facts about SCR
![]() $_{XY}$
from BGS [Proposition 7.3 and Corollary 7.4] that include its being a THA and then a couple of variations along the lines described above that produce ATHAs.
$_{XY}$
from BGS [Proposition 7.3 and Corollary 7.4] that include its being a THA and then a couple of variations along the lines described above that produce ATHAs.
Proposition 5.6. (RCA
![]() $_{0}$
) SCR
$_{0}$
) SCR
![]() $_{XY}~\rightarrow ~$
ACA
$_{XY}~\rightarrow ~$
ACA
![]() $_{0}$
.
$_{0}$
.
Corollary 5.7. (RCA
![]() $_{0}$
) SCR
$_{0}$
) SCR
![]() $_{XY}~\Leftrightarrow ~$
IRT
$_{XY}~\Leftrightarrow ~$
IRT
![]() $_{XY}$
.
$_{XY}$
.
Definition 5.8. A sequence
![]() $\left \langle x_{n}\right \rangle $
of vertices in an X-graph G is almost an X-ray in G if, for some k,
$\left \langle x_{n}\right \rangle $
of vertices in an X-graph G is almost an X-ray in G if, for some k,
![]() $\left \langle x_{k+n}\right \rangle $
is an X-ray in G. A sequence
$\left \langle x_{k+n}\right \rangle $
is an X-ray in G. A sequence
![]() $\left \langle X_{n}\right \rangle $
of almost X-rays
$\left \langle X_{n}\right \rangle $
of almost X-rays
![]() $\left \langle x_{n,i}\right \rangle $
is almost Y-disjoint if for every
$\left \langle x_{n,i}\right \rangle $
is almost Y-disjoint if for every
![]() $n\neq m$
there are only finitely many
$n\neq m$
there are only finitely many
![]() $i,j$
such that
$i,j$
such that
![]() $x_{n,i}=x_{m,j}$
(for
$x_{n,i}=x_{m,j}$
(for
![]() $Y=V$
). For
$Y=V$
). For
![]() $Y=E$
we require that there are only finitely many
$Y=E$
we require that there are only finitely many
![]() $i,j$
such that
$i,j$
such that
![]() $ (x_{n,i},x_{n,i+1})=(x_{m,j},x_{m,j+1})$
.
$ (x_{n,i},x_{n,i+1})=(x_{m,j},x_{m,j+1})$
.
Definition 5.9 (SCR
 $_{XY}^{\ast }$
).
$_{XY}^{\ast }$
).
If an X-graph G has arbitrarily many pairwise almost Y-disjoint almost X-rays then there is a Z such that, for each k,
![]() $Z^{[k]}$
is a sequence
$Z^{[k]}$
is a sequence
![]() $\left \langle Z_{k,i}|1\leq i\leq k\right \rangle $
of pairwise almost Y-disjoint almost X-rays in G. (Note the use of
$\left \langle Z_{k,i}|1\leq i\leq k\right \rangle $
of pairwise almost Y-disjoint almost X-rays in G. (Note the use of
![]() $\ast $
here and in later such principles is suggested by the common usage of
$\ast $
here and in later such principles is suggested by the common usage of
![]() $=^{\ast }$
to mean equal up to finite difference and is not related to the induction axioms characterizing, e.g., ACA
$=^{\ast }$
to mean equal up to finite difference and is not related to the induction axioms characterizing, e.g., ACA
![]() $_{0}^{\ast }$
and related principles in BGS.)
$_{0}^{\ast }$
and related principles in BGS.)
Definition 5.10 (SCR
 $_{XY}^{-}$
).
$_{XY}^{-}$
).
If an X-graph G has arbitrarily many pairwise almost
![]() $ Y $
-disjoint almost X-rays then there is a Z such that, for each k, there is an l such that
$ Y $
-disjoint almost X-rays then there is a Z such that, for each k, there is an l such that
![]() $Z^{[l]}$
is a sequence
$Z^{[l]}$
is a sequence
![]() $\left \langle Z_{k,i}|1\leq i\leq k\right \rangle $
of pairwise almost Y-disjoint almost
$\left \langle Z_{k,i}|1\leq i\leq k\right \rangle $
of pairwise almost Y-disjoint almost
![]() $ X$
-rays in G.
$ X$
-rays in G.
Clearly each of ACA
![]() $_{0}$
+ SCR
$_{0}$
+ SCR
![]() $_{XY}^{\ast }$
and ACA
$_{XY}^{\ast }$
and ACA
![]() $_{0}$
+SCR
$_{0}$
+SCR
![]() $_{XY}^{-}$
imply SCR
$_{XY}^{-}$
imply SCR
![]() $_{XY}$
, a THA. Thus to show that SCR
$_{XY}$
, a THA. Thus to show that SCR
![]() $_{XY}^{\ast }$
and SCR
$_{XY}^{\ast }$
and SCR
![]() $ _{XY}^{-}$
are ATHAs, we only have to show that they do not imply ACA
$ _{XY}^{-}$
are ATHAs, we only have to show that they do not imply ACA
![]() $_{0}$
. As should be expected, all eight variants have solutions provided by et-forcings and so satisfy all the conclusions of Theorems 4.11 –4.13. However, instead of presenting specific forcing notions for them we turn to
$_{0}$
. As should be expected, all eight variants have solutions provided by et-forcings and so satisfy all the conclusions of Theorems 4.11 –4.13. However, instead of presenting specific forcing notions for them we turn to
![]() $\Sigma _{1}^{1}$
-AC. It is clear that it implies SCR
$\Sigma _{1}^{1}$
-AC. It is clear that it implies SCR
![]() $_{XY}$
. The
$_{XY}$
. The
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $^{-}$
analogs for it also imply those of SCR
$^{-}$
analogs for it also imply those of SCR
![]() $_{XY}$
and we provide the notions of forcing for them instead. This then shows that all of these principles are ATHAs. We will then consider other well studied weakenings of
$_{XY}$
and we provide the notions of forcing for them instead. This then shows that all of these principles are ATHAs. We will then consider other well studied weakenings of
![]() $\Sigma _{1}^{1}$
-AC which are THAs but whose
$\Sigma _{1}^{1}$
-AC which are THAs but whose
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $ ^{-}$
analogs will also be ATHAs. In the next section we turn to stronger versions of choice which are too strong to be THAs but whose
$ ^{-}$
analogs will also be ATHAs. In the next section we turn to stronger versions of choice which are too strong to be THAs but whose
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $ ^{-}$
variants also have all of the same weakness properties over RCA
$ ^{-}$
variants also have all of the same weakness properties over RCA
![]() $_{0}$
.
$_{0}$
.
Remark 5.11. We make an brief exception to Remark 2.6 to sketch one consideration of double rays in directed graphs because we can get ATHAs which yield equivalences with a standard theory. We say a sequence
![]() $ \left \langle x_{n}|n\in \mathbb {Z}\right \rangle $
of vertices in a D-graph G is almost a double directed ray in G if changing finitely many of the
$ \left \langle x_{n}|n\in \mathbb {Z}\right \rangle $
of vertices in a D-graph G is almost a double directed ray in G if changing finitely many of the
![]() $x_{n}$
to a different vertex or removing it from the list (and reindexing) produces a double directed ray. From the natural analogs SCR
$x_{n}$
to a different vertex or removing it from the list (and reindexing) produces a double directed ray. From the natural analogs SCR
![]() $ _{DYD}$
for double Y-disjoint directed rays we form the analogous SCR
$ _{DYD}$
for double Y-disjoint directed rays we form the analogous SCR
![]() $ _{DYD}^{\ast }$
and SCR
$ _{DYD}^{\ast }$
and SCR
![]() $_{DYD}^{-}$
where, as we have allowed removing vertices in the definition of almost rays, we use full Y-disjointness. As for SCR
$_{DYD}^{-}$
where, as we have allowed removing vertices in the definition of almost rays, we use full Y-disjointness. As for SCR
![]() $_{XY}$
, these are also consequences of
$_{XY}$
, these are also consequences of
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $ _{0}^{\ast }$
and
$ _{0}^{\ast }$
and
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}^{-}$
, respectively and so weak over RCA
$_{0}^{-}$
, respectively and so weak over RCA
![]() $_{0}$
. On the other hand, it is easy to see from the proof of BGS [Theorem 6.13] that, as for SCR
$_{0}$
. On the other hand, it is easy to see from the proof of BGS [Theorem 6.13] that, as for SCR
![]() $_{XY}$
, SCR
$_{XY}$
, SCR
![]() $_{DYD}^{\ast }$
, and SCR
$_{DYD}^{\ast }$
, and SCR
![]() $ _{DYD}^{-}$
restricted to directed forests (i.e., directed graphs whose underlying graph gotten by symmetrizing the edge relation is a disjoint union of trees) plus ACA
$ _{DYD}^{-}$
restricted to directed forests (i.e., directed graphs whose underlying graph gotten by symmetrizing the edge relation is a disjoint union of trees) plus ACA
![]() $_{0}$
is equivalent to
$_{0}$
is equivalent to
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
over I
$_{0}$
over I
![]() $\Sigma _{1}^{1}$
. Thus we have two more mathematical ATHAs for which we actually know that, with the addition of ACA
$\Sigma _{1}^{1}$
. Thus we have two more mathematical ATHAs for which we actually know that, with the addition of ACA
![]() $_{0}$
, they are equivalent to
$_{0}$
, they are equivalent to
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
over I
$_{0}$
over I
![]() $\Sigma _{1}^{1}$
.
$\Sigma _{1}^{1}$
.
As there is some variation in the formulations of these principles in the literature, we want to make the versions and the relations among them explicit. We begin with
![]() $\Sigma _{1}^{1}$
-AC itself which is a THA.
$\Sigma _{1}^{1}$
-AC itself which is a THA.
Definition 5.12.
![]() $\Sigma _{1}^{1}$
-AC is the principle
$\Sigma _{1}^{1}$
-AC is the principle
![]() $\forall A[\forall n\exists X\Phi (n,X)\rightarrow \exists Y\forall n\Phi (n,Y^{[n]})]$
. Here
$\forall A[\forall n\exists X\Phi (n,X)\rightarrow \exists Y\forall n\Phi (n,Y^{[n]})]$
. Here
![]() $ \Phi $
is an arithmetic formula possibly with free set variables A and X but not Y. (We take these restrictions on the free set variables for granted in all future similar situations.) Equivalently (over RCA
$ \Phi $
is an arithmetic formula possibly with free set variables A and X but not Y. (We take these restrictions on the free set variables for granted in all future similar situations.) Equivalently (over RCA
![]() $_{0})$
, we may allow
$_{0})$
, we may allow
![]() $\Phi $
to be
$\Phi $
to be
![]() $\Sigma _{1}^{1}$
.
$\Sigma _{1}^{1}$
.
One direction of this equivalence in RCA
![]() $_{0}$
is immediate as all arithmetic formulas are trivially equivalent to
$_{0}$
is immediate as all arithmetic formulas are trivially equivalent to
![]() $\Sigma _{1}^{1}$
formulas. For the other direction consider
$\Sigma _{1}^{1}$
formulas. For the other direction consider
![]() $\Phi =\exists Z\Psi (A,n,X,Z)$
(
$\Phi =\exists Z\Psi (A,n,X,Z)$
(
![]() $\Psi $
arithmetic). One simply considers the instance
$\Psi $
arithmetic). One simply considers the instance
![]() $\forall n\exists X\Psi (A,n,X^{[0]},X^{[1]})$
. Clearly one can recursively recover the Y required for
$\forall n\exists X\Psi (A,n,X^{[0]},X^{[1]})$
. Clearly one can recursively recover the Y required for
![]() $\Phi $
from the one given by
$\Phi $
from the one given by
![]() $\Sigma _{1}^{1}$
-AC for
$\Sigma _{1}^{1}$
-AC for
![]() $\Psi (A,n,X^{[0]},X^{[1]})$
. We choose the version with
$\Psi (A,n,X^{[0]},X^{[1]})$
. We choose the version with
![]() $\Phi $
arithmetic to match the common terminology for weak
$\Phi $
arithmetic to match the common terminology for weak
![]() $\Sigma _{1}^{1}$
-AC (U-
$\Sigma _{1}^{1}$
-AC (U-
![]() $\Sigma _{1}^{1}$
-AC below). On the other hand, there is another common a priori weaker version for which the proof of the equivalence uses ACA
$\Sigma _{1}^{1}$
-AC below). On the other hand, there is another common a priori weaker version for which the proof of the equivalence uses ACA
![]() $_{0}$
. This is not an issue for
$_{0}$
. This is not an issue for
![]() $\Sigma _{1}^{1}$
-AC as even this “weaker” version implies ACA
$\Sigma _{1}^{1}$
-AC as even this “weaker” version implies ACA
![]() $_{0}$
. This will no longer be true of our
$_{0}$
. This will no longer be true of our
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $^{-}$
variants.
$^{-}$
variants.
Proposition 5.13 (ACA
 $_{0}$
).
$_{0}$
).
![]() $\Sigma _{1}^{1}$
-AC is equivalent to the principle TAC: For every sequence
$\Sigma _{1}^{1}$
-AC is equivalent to the principle TAC: For every sequence
![]() $T_{i}$
of trees, if
$T_{i}$
of trees, if
![]() $\forall n\exists f(f\in \lbrack T_{i}])$
, then
$\forall n\exists f(f\in \lbrack T_{i}])$
, then
![]() $\exists f\forall n(f^{[n]}\in \lbrack T_{n}])$
.
$\exists f\forall n(f^{[n]}\in \lbrack T_{n}])$
.
This proposition is well known and follows easily from the normal form theorem proved in ACA
![]() $_{0}$
as Lemma V.5.4 of [Reference Simpson28].
$_{0}$
as Lemma V.5.4 of [Reference Simpson28].
We now define our variants of
![]() $\Sigma _{1}^{1}$
-AC.
$\Sigma _{1}^{1}$
-AC.
Notation 5.14. For a function f, finite string
![]() $\mu $
(or set X), and
$\mu $
(or set X), and
![]() $\sigma $
a finite (binary) string we write
$\sigma $
a finite (binary) string we write
![]() $f_{\sigma }$
,
$f_{\sigma }$
,
![]() $\mu _{\sigma }$
(or
$\mu _{\sigma }$
(or
![]() $X_{\sigma }$
) to mean the function, finite string (or set) gotten by using
$X_{\sigma }$
) to mean the function, finite string (or set) gotten by using
![]() $\sigma $
to define its initial segment of length
$\sigma $
to define its initial segment of length
![]() $|\sigma |$
:
$|\sigma |$
:
![]() $f_{\sigma }(i)=\sigma (i)$
for
$f_{\sigma }(i)=\sigma (i)$
for
![]() $i<|\sigma |$
,
$i<|\sigma |$
,
![]() $f_{\sigma }(i)=f(i)$
for
$f_{\sigma }(i)=f(i)$
for
![]() $i\geq |\sigma |$
and similarly for
$i\geq |\sigma |$
and similarly for
![]() $\mu _{\sigma }$
and
$\mu _{\sigma }$
and
![]() $X_{\sigma }$
. We write
$X_{\sigma }$
. We write
![]() $f_{\sigma }^{[n]}$
for
$f_{\sigma }^{[n]}$
for
![]() $ (f^{[n]})_{\sigma }$
and
$ (f^{[n]})_{\sigma }$
and
![]() $X_{\sigma }^{[n]}$
for
$X_{\sigma }^{[n]}$
for
![]() $(X^{[n]})_{\sigma }$
. Similarly, for a tree T we write
$(X^{[n]})_{\sigma }$
. Similarly, for a tree T we write
![]() $T_{\sigma }=\{\mu _{\sigma }|\mu \in T\}$
. We write
$T_{\sigma }=\{\mu _{\sigma }|\mu \in T\}$
. We write
![]() $T_{\rho }^{\sigma }$
for
$T_{\rho }^{\sigma }$
for
![]() $(T^{\sigma })_{\rho }$
where
$(T^{\sigma })_{\rho }$
where
![]() $ T^{\sigma }$
is defined in Notation 4.3.
$ T^{\sigma }$
is defined in Notation 4.3.
Definition 5.15. For
![]() $\Phi $
arithmetic:
$\Phi $
arithmetic:
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
:
$^{\ast }$
:
![]() $\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\exists \sigma \Phi (A,n,Y_{\sigma }^{[n]})]$
and
$\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\exists \sigma \Phi (A,n,Y_{\sigma }^{[n]})]$
and
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{-}$
:
$^{-}$
:
![]() $\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\exists m\Phi (A,n,Y^{[m]})]$
.
$\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\exists m\Phi (A,n,Y^{[m]})]$
.
TAC
![]() $^{\ast }$
: For every sequence
$^{\ast }$
: For every sequence
![]() $\left \langle T_{n}\right \rangle $
of trees, if
$\left \langle T_{n}\right \rangle $
of trees, if
![]() $\forall n\exists f(f\in \lbrack T_{n}])$
then
$\forall n\exists f(f\in \lbrack T_{n}])$
then
![]() $\exists f\forall n\exists \sigma (f_{\sigma }^{[n]}\in \lbrack T_{n}])$
.
$\exists f\forall n\exists \sigma (f_{\sigma }^{[n]}\in \lbrack T_{n}])$
.
TAC
![]() $^{-}$
: For every sequence
$^{-}$
: For every sequence
![]() $\left \langle T_{n}\right \rangle $
of trees, if
$\left \langle T_{n}\right \rangle $
of trees, if
![]() $\forall n\exists f(f\in \lbrack T_{n}])$
then
$\forall n\exists f(f\in \lbrack T_{n}])$
then
![]() $\exists f\forall n\exists m(f^{[m]}\in \lbrack T_{n}])$
.
$\exists f\forall n\exists m(f^{[m]}\in \lbrack T_{n}])$
.
As with
![]() $\Sigma _{1}^{1}$
-AC,
$\Sigma _{1}^{1}$
-AC,
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{-}$
are each equivalent (over RCA
$^{-}$
are each equivalent (over RCA
![]() $_{0}$
) to the analogous principle with
$_{0}$
) to the analogous principle with
![]() $\Phi $
being
$\Phi $
being
![]() $\Sigma _{1}^{1}$
.
$\Sigma _{1}^{1}$
.
Proposition 5.16. In RCA
![]() $_{0}$
,
$_{0}$
,
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $\rightarrow \Sigma _{1}^{1}$
-AC
$\rightarrow \Sigma _{1}^{1}$
-AC
![]() $^{\kern1.2pt \ast }\rightarrow \Sigma _{1}^{1}$
-AC
$^{\kern1.2pt \ast }\rightarrow \Sigma _{1}^{1}$
-AC
![]() $^{\kern1.2pt -}~\&~$
TAC
$^{\kern1.2pt -}~\&~$
TAC
![]() $^{\kern1.2pt \ast }$
;
$^{\kern1.2pt \ast }$
;
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\kern1.2pt -}\rightarrow $
TAC
$^{\kern1.2pt -}\rightarrow $
TAC
![]() $^{\kern1.2pt -}$
; TAC
$^{\kern1.2pt -}$
; TAC
![]() $^{\kern1.2pt \ast }\rightarrow $
TAC
$^{\kern1.2pt \ast }\rightarrow $
TAC
![]() $^{\kern1.2pt -}$
and TAC
$^{\kern1.2pt -}$
and TAC
![]() $^{\kern1.2pt -}\rightarrow $
TAC
$^{\kern1.2pt -}\rightarrow $
TAC
![]() $^{\kern1.2pt \ast }$
. In ACA
$^{\kern1.2pt \ast }$
. In ACA
![]() $_{0}$
all of these principles are equivalent to
$_{0}$
all of these principles are equivalent to
![]() $\Sigma _{1}^{1}$
-AC.
$\Sigma _{1}^{1}$
-AC.
Proof The implication
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $\rightarrow \Sigma _{1}^{1}$
-AC
$\rightarrow \Sigma _{1}^{1}$
-AC
![]() $^{\kern1.2pt \ast } $
is immediate as solutions to instances of the former are also solutions to the same instance of the latter. The implications from a
$^{\kern1.2pt \ast } $
is immediate as solutions to instances of the former are also solutions to the same instance of the latter. The implications from a
![]() $^{\ast }$
version to the corresponding
$^{\ast }$
version to the corresponding
![]() $^{-}$
one in RCA
$^{-}$
one in RCA
![]() $_{0}$
are essentially instances of Proposition 5.4. Of course, the versions of TAC are simply special cases of the corresponding one for
$_{0}$
are essentially instances of Proposition 5.4. Of course, the versions of TAC are simply special cases of the corresponding one for
![]() $\Sigma _{1}^{1}$
-AC. (The
$\Sigma _{1}^{1}$
-AC. (The
![]() $ \left \langle T_{i}\right \rangle $
is absorbed into the set parameters.) For the equivalences in ACA
$ \left \langle T_{i}\right \rangle $
is absorbed into the set parameters.) For the equivalences in ACA
![]() $_{0}$
it thus suffices to show that TAC
$_{0}$
it thus suffices to show that TAC
![]() $ ^{-}\rightarrow \Sigma _{1}^{1}$
-AC
$ ^{-}\rightarrow \Sigma _{1}^{1}$
-AC
![]() $_{0}$
. First note that TAC follows from TAC
$_{0}$
. First note that TAC follows from TAC
![]() $^{-}$
in ACA
$^{-}$
in ACA
![]() $_{0}$
as, given an instance of TAC and the f provided by TAC
$_{0}$
as, given an instance of TAC and the f provided by TAC
![]() $^{-}$
, one can construct the one required by TAC recursively in the jump of f and the given sequence of trees. Now we have
$^{-}$
, one can construct the one required by TAC recursively in the jump of f and the given sequence of trees. Now we have
![]() $\Sigma _{1}^{1}$
-AC by Proposition 5.13.
$\Sigma _{1}^{1}$
-AC by Proposition 5.13.
Finally that RCA
![]() $_{0}\vdash ~$
TAC
$_{0}\vdash ~$
TAC
![]() $^{-}\rightarrow $
TAC
$^{-}\rightarrow $
TAC
![]() $^{\ast }$
requires an argument that does not work for the
$^{\ast }$
requires an argument that does not work for the
![]() $\Sigma _{1}^{1}$
-AC analogs. We are given a sequence
$\Sigma _{1}^{1}$
-AC analogs. We are given a sequence
![]() $\left \langle T_{n}\right \rangle $
of trees such that
$\left \langle T_{n}\right \rangle $
of trees such that
![]() $ \forall n\exists f(f\in \lbrack T_{n}])$
and an f such that
$ \forall n\exists f(f\in \lbrack T_{n}])$
and an f such that
![]() $\forall n\exists m(f^{[m]}\in \lbrack T_{n}])$
and must produce a g such that
$\forall n\exists m(f^{[m]}\in \lbrack T_{n}])$
and must produce a g such that
![]() $ \forall n\exists \sigma (g_{\sigma }^{[n]}\in \lbrack T_{n}]$
. To construct
$ \forall n\exists \sigma (g_{\sigma }^{[n]}\in \lbrack T_{n}]$
. To construct
![]() $ g^{[n]}$
we start by copying
$ g^{[n]}$
we start by copying
![]() $f^{[0]}$
until we have an
$f^{[0]}$
until we have an
![]() $s_{0}$
such that
$s_{0}$
such that
![]() $ f^{[0]}\upharpoonright s_{0}+1\notin T_{n}.$
If we never find such an s we have computed a branch on
$ f^{[0]}\upharpoonright s_{0}+1\notin T_{n}.$
If we never find such an s we have computed a branch on
![]() $T_{n}$
and so
$T_{n}$
and so
![]() $g^{[n]}=g_{\emptyset }^{[n]}$
is as required. If we find such an
$g^{[n]}=g_{\emptyset }^{[n]}$
is as required. If we find such an
![]() $s_{0}$
we switch to copying
$s_{0}$
we switch to copying
![]() $f^{[1]}$
for inputs from
$f^{[1]}$
for inputs from
![]() $s_{0}$
onward. We continue until we once again fall off
$s_{0}$
onward. We continue until we once again fall off
![]() $T_{n}$
, i.e.,
$T_{n}$
, i.e.,
![]() $f^{[1]}\upharpoonright s_{1}+1\notin T_{n}$
. By the conclusion of TAC
$f^{[1]}\upharpoonright s_{1}+1\notin T_{n}$
. By the conclusion of TAC
![]() $^{-}$
from some point onward there is a fixed m such that we are copying
$^{-}$
from some point onward there is a fixed m such that we are copying
![]() $ f^{[m]}$
and
$ f^{[m]}$
and
![]() $f^{[m]}\in \lbrack T_{n}]$
. We have thus constructed a g such that
$f^{[m]}\in \lbrack T_{n}]$
. We have thus constructed a g such that
![]() $g_{\sigma }\in \lbrack T_{n}]$
with
$g_{\sigma }\in \lbrack T_{n}]$
with
![]() $\sigma =f^{[m]}\upharpoonright s_{m-1}$
.
$\sigma =f^{[m]}\upharpoonright s_{m-1}$
.
We do not know if RCA
![]() $_{0}\vdash \Sigma _{1}^{1}$
-AC
$_{0}\vdash \Sigma _{1}^{1}$
-AC
![]() $^{-} \ \rightarrow \ \Sigma _{1}^{1}$
-AC
$^{-} \ \rightarrow \ \Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
. We also note other views of
$^{\ast }$
. We also note other views of
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{-}$
.
$^{-}$
.
Proposition 5.17. In RCA
![]() $_{0}$
,
$_{0}$
,
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
is equivalent to
$^{\ast }$
is equivalent to
![]() $\Sigma _{1}^{1}$
-AC restricted to predicates
$\Sigma _{1}^{1}$
-AC restricted to predicates
![]() $\Phi (A,n,X)$
that are invariant under finite changes in X, i.e.,
$\Phi (A,n,X)$
that are invariant under finite changes in X, i.e.,
![]() $\forall A\forall n\forall X\forall \sigma (\Phi (A,n,X)\Leftrightarrow \Phi (A,n,X_{\sigma }))$
.
$\forall A\forall n\forall X\forall \sigma (\Phi (A,n,X)\Leftrightarrow \Phi (A,n,X_{\sigma }))$
.
Proof If a given instance
![]() $\Phi (A,n,X)$
of
$\Phi (A,n,X)$
of
![]() $\Sigma _{1}^{1}$
-AC is invariant under finite changes then a solution for the same instance of
$\Sigma _{1}^{1}$
-AC is invariant under finite changes then a solution for the same instance of
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
is also one for
$^{\ast }$
is also one for
![]() $\Sigma _{1}^{1}$
-AC. In the other direction, given an instance
$\Sigma _{1}^{1}$
-AC. In the other direction, given an instance
![]() $\Phi (A,n,X)$
of
$\Phi (A,n,X)$
of
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
, consider the one
$^{\ast }$
, consider the one
![]() $\Psi (A,n,X)\equiv \exists \sigma \Phi (A,n,X_{\sigma })$
for
$\Psi (A,n,X)\equiv \exists \sigma \Phi (A,n,X_{\sigma })$
for
![]() $\Sigma _{1}^{1}$
-AC. Clearly
$\Sigma _{1}^{1}$
-AC. Clearly
![]() $\Psi (A,n,X)$
is closed under finite changes and any
$\Psi (A,n,X)$
is closed under finite changes and any
![]() $\Sigma _{1}^{1}$
-AC solution for
$\Sigma _{1}^{1}$
-AC solution for
![]() $\Psi $
is also a
$\Psi $
is also a
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
solution for the
$^{\ast }$
solution for the
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
instance
$^{\ast }$
instance
![]() $\Phi (A,n,X)$
.
$\Phi (A,n,X)$
.
As for
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{-}$
, when we told some people about some of the results in this paper both Antonio Montalbán and Keita Yokoyama informed us of some early work by Tanaka, Yamazaki, and Montalbán on variations of choice principles. In particular, they considered
$^{-}$
, when we told some people about some of the results in this paper both Antonio Montalbán and Keita Yokoyama informed us of some early work by Tanaka, Yamazaki, and Montalbán on variations of choice principles. In particular, they considered
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{-}$
under the natural name
$^{-}$
under the natural name
![]() $\Sigma _{1}^{1}$
-collection as well as the natural generalizations we call
$\Sigma _{1}^{1}$
-collection as well as the natural generalizations we call
![]() $\Sigma _{n}^{1}$
-AC
$\Sigma _{n}^{1}$
-AC
![]() $^{-}$
and
$^{-}$
and
![]() $ \Sigma _{\infty }^{1}$
-AC
$ \Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
under the names
$^{-}$
under the names
![]() $\Pi _{n}^{1}$
-collection and
$\Pi _{n}^{1}$
-collection and
![]() $\Pi _{\infty }^{1}$
-collection and proved several conservation results. We discuss those results in Section 7.
$\Pi _{\infty }^{1}$
-collection and proved several conservation results. We discuss those results in Section 7.
Theorem 5.18. For each of the
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $^{-}$
versions of
$^{-}$
versions of
![]() $\Sigma _{1}^{1}$
-AC in Definition 5.15 solutions can be provided by et-forcings. Thus they are G-r-
$\Sigma _{1}^{1}$
-AC in Definition 5.15 solutions can be provided by et-forcings. Thus they are G-r-
![]() $\Pi _{2}^{1}$
(and so G-r-
$\Pi _{2}^{1}$
(and so G-r-
![]() $\Pi _{1}^{1}$
) conservative over RCA
$\Pi _{1}^{1}$
) conservative over RCA
![]() $_{0}$
. Moreover, they can be realized in extensions that omit branches (and so avoid cones) as in Theorem 4.13.
$_{0}$
. Moreover, they can be realized in extensions that omit branches (and so avoid cones) as in Theorem 4.13.
Proof By Proposition 5.16 it suffices to prove the theorem for
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
. Given a countable model
$^{\ast }$
. Given a countable model
![]() $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
![]() $_{0}$
and an arithmetic
$_{0}$
and an arithmetic
![]() $\Phi $
such that
$\Phi $
such that
![]() $\mathcal {N}\vDash \forall n\exists X\Phi (A,n,X)$
we define a forcing with conditions
$\mathcal {N}\vDash \forall n\exists X\Phi (A,n,X)$
we define a forcing with conditions
![]() $\left \langle \tau ,T\right \rangle $
such that, in
$\left \langle \tau ,T\right \rangle $
such that, in
![]() $\mathcal {N}$
, there is a finite set F and a sequence
$\mathcal {N}$
, there is a finite set F and a sequence
![]() $\left \langle X_{i}|i\in F\right \rangle $
such that
$\left \langle X_{i}|i\in F\right \rangle $
such that
![]() $\forall i\in F\Phi (A,i,X_{i})$
and for all
$\forall i\in F\Phi (A,i,X_{i})$
and for all
![]() $\sigma \in T$
,
$\sigma \in T$
,
![]() $|\sigma |>n\geq |\tau |$
with
$|\sigma |>n\geq |\tau |$
with
![]() $n=\left \langle i,m\right \rangle $
for some
$n=\left \langle i,m\right \rangle $
for some
![]() $i\in F$
,
$i\in F$
,
![]() $\sigma (n)=X_{i}(m)$
. (Otherwise there are no restrictions on
$\sigma (n)=X_{i}(m)$
. (Otherwise there are no restrictions on
![]() $\sigma $
.)
$\sigma $
.)
It is now easy to see that the associated notion of forcing is et: If
![]() $ \left \langle \tau ,T\right \rangle $
is a condition and
$ \left \langle \tau ,T\right \rangle $
is a condition and
![]() $\sigma \in T$
then
$\sigma \in T$
then
![]() $ \left \langle \sigma ,T^{\sigma }\right \rangle $
is a condition with the same F and
$ \left \langle \sigma ,T^{\sigma }\right \rangle $
is a condition with the same F and
![]() $X_{i}$
which extends
$X_{i}$
which extends
![]() $\left \langle \tau ,T\right \rangle $
. It is also clear the sets
$\left \langle \tau ,T\right \rangle $
. It is also clear the sets
![]() $D_{i}$
of conditions such that i is a member of the associated F are dense. (Just thin out a given
$D_{i}$
of conditions such that i is a member of the associated F are dense. (Just thin out a given
![]() $\left \langle \tau ,T\right \rangle $
by choosing an
$\left \langle \tau ,T\right \rangle $
by choosing an
![]() $X_{i}$
such that
$X_{i}$
such that
![]() $\Phi (A,i,X_{i})$
and keeping only those
$\Phi (A,i,X_{i})$
and keeping only those
![]() $\sigma \in T$
which satisfy the condition that
$\sigma \in T$
which satisfy the condition that
![]() $\sigma (\left \langle i,m\right \rangle )=X_{i}(m)$
for
$\sigma (\left \langle i,m\right \rangle )=X_{i}(m)$
for
![]() $\left \langle i,m\right \rangle \geq |\tau |$
.) Moreover, for any G on this thinned out tree,
$\left \langle i,m\right \rangle \geq |\tau |$
.) Moreover, for any G on this thinned out tree,
![]() $G^{[i]}=^{\ast }X_{i}$
. Thus for any G generic for these
$G^{[i]}=^{\ast }X_{i}$
. Thus for any G generic for these
![]() $D_{i}$
,
$D_{i}$
,
![]() $ G $
is the desired witness for this instance of
$ G $
is the desired witness for this instance of
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast } $
.
$^{\ast } $
.
The argument in the proof of Theorem 5.2 now shows that all the desired properties hold for these choice principles as well.
We now turn to
![]() $\Sigma _{1}^{1}$
-AC itself and some of its choice like consequences. Each of them has versions with the property
$\Sigma _{1}^{1}$
-AC itself and some of its choice like consequences. Each of them has versions with the property
![]() $\Psi (i,Y)$
required of the
$\Psi (i,Y)$
required of the
![]() $X_{i}$
being arithmetic or equivalently
$X_{i}$
being arithmetic or equivalently
![]() $\Sigma _{1}^{1}$
and versions with it being
$\Sigma _{1}^{1}$
and versions with it being
![]() $\Pi _{2}^{0}$
or equivalently asking for a branch on a tree
$\Pi _{2}^{0}$
or equivalently asking for a branch on a tree
![]() $T_{i}$
in a uniform sequence of trees. These are easily seen to be equivalent over ACA
$T_{i}$
in a uniform sequence of trees. These are easily seen to be equivalent over ACA
![]() $_{0}$
but not over RCA
$_{0}$
but not over RCA
![]() $_{0}$
. In particular, we want to consider the versions where we restrict the principles to
$_{0}$
. In particular, we want to consider the versions where we restrict the principles to
![]() $\Phi $
such that, for each n, there are only finitely many X for which
$\Phi $
such that, for each n, there are only finitely many X for which
![]() $\Phi (A,n,X)$
holds (F-
$\Phi (A,n,X)$
holds (F-
![]() $\Sigma _{1}^{1}$
-AC) or exactly one such X (U-
$\Sigma _{1}^{1}$
-AC) or exactly one such X (U-
![]() $\Sigma _{1}^{1}$
-AC) which is generally called weak
$\Sigma _{1}^{1}$
-AC) which is generally called weak
![]() $\Sigma _{1}^{1}$
-AC. These can also be phrased in terms of sequences
$\Sigma _{1}^{1}$
-AC. These can also be phrased in terms of sequences
![]() $\left \langle T_{i}\right \rangle $
of trees as in TAC by restricting to
$\left \langle T_{i}\right \rangle $
of trees as in TAC by restricting to
![]() $T_{i}$
with only finitely many or exactly one branch. We will explicitly just consider the
$T_{i}$
with only finitely many or exactly one branch. We will explicitly just consider the
![]() $\Sigma _{1}^{1}$
-AC versions. We are here interested in the
$\Sigma _{1}^{1}$
-AC versions. We are here interested in the
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $^{-}$
versions.
$^{-}$
versions.
Theorem 5.19. RCA
![]() $_{0}\vdash \Sigma _{1}^{1}$
-AC
$_{0}\vdash \Sigma _{1}^{1}$
-AC
![]() $^{\ast }\rightarrow $
F-
$^{\ast }\rightarrow $
F-
![]() $ \Sigma _{1}^{1}$
-AC
$ \Sigma _{1}^{1}$
-AC
![]() $^{\ast }\rightarrow $
U-
$^{\ast }\rightarrow $
U-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
. None of these implications can be reversed and all of these principles are ATHAs. The same holds for the
$^{\ast }$
. None of these implications can be reversed and all of these principles are ATHAs. The same holds for the
![]() $^{-}$
versions.
$^{-}$
versions.
Proof We consider the
![]() $^{\ast }$
versions but all the arguments apply to the
$^{\ast }$
versions but all the arguments apply to the
![]() $^{-}$
ones as well.
$^{-}$
ones as well.
It is obvious that
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}\rightarrow \Sigma _{1}^{1}$
-AC
$_{0}\rightarrow \Sigma _{1}^{1}$
-AC
![]() $ ^{\ast }\rightarrow $
F-
$ ^{\ast }\rightarrow $
F-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }\rightarrow $
U-
$^{\ast }\rightarrow $
U-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
in RCA
$^{\ast }$
in RCA
![]() $_{0}$
. As in Proposition 5.16, it is easy to see that with the addition of ACA
$_{0}$
. As in Proposition 5.16, it is easy to see that with the addition of ACA
![]() $_{0}$
each of the
$_{0}$
each of the
![]() $^{\ast }$
principles is equivalent to the standard unstarred version. Each of the standard principles is a THA (see [Reference Montalbán21, p. 564], the references therein, and [Reference Goh9]). Theorem 5.18 shows that none of them implies ACA
$^{\ast }$
principles is equivalent to the standard unstarred version. Each of the standard principles is a THA (see [Reference Montalbán21, p. 564], the references therein, and [Reference Goh9]). Theorem 5.18 shows that none of them implies ACA
![]() $_{0}$
(over RCA
$_{0}$
(over RCA
![]() $_{0})$
and so are all ATHAs. The known separations of all of the unstarred versions provide witnesses that are even standard models of much more than ACA
$_{0})$
and so are all ATHAs. The known separations of all of the unstarred versions provide witnesses that are even standard models of much more than ACA
![]() $_{0}$
(see [Reference Goh9, Reference Steel30, Reference Van Wesep31]). They then are also witnesses for the nonimplications among the
$_{0}$
(see [Reference Goh9, Reference Steel30, Reference Van Wesep31]). They then are also witnesses for the nonimplications among the
![]() $ ^{\ast }$
versions.
$ ^{\ast }$
versions.
6 Higher choice principles
In this section we want to study the
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $^{-}$
variations of choice principles that replace the arithmetic formulas
$^{-}$
variations of choice principles that replace the arithmetic formulas
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
in
$\Psi $
in
![]() $\Sigma _{1}^{1}$
-AC by arbitrary formulas. The usual terminology has
$\Sigma _{1}^{1}$
-AC by arbitrary formulas. The usual terminology has
![]() $ \Sigma _{n+1}^{1}$
-AC being the principle
$ \Sigma _{n+1}^{1}$
-AC being the principle
![]() $\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\Phi (A,n,Y^{[n]})]$
for
$\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\Phi (A,n,Y^{[n]})]$
for
![]() $\Phi \ \Sigma _{n+1}^{1}$
. As with
$\Phi \ \Sigma _{n+1}^{1}$
. As with
![]() $\Sigma _{1}^{1}$
these and their
$\Sigma _{1}^{1}$
these and their
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $^{-}$
versions are equivalent to the ones with
$^{-}$
versions are equivalent to the ones with
![]() $\Phi $
being
$\Phi $
being
![]() $\Pi _{n}^{1}$
. We take the
$\Pi _{n}^{1}$
. We take the
![]() $\Pi _{n}^{1}$
versions to be our official definitions for notational convenience. As usual
$\Pi _{n}^{1}$
versions to be our official definitions for notational convenience. As usual
![]() $\Sigma _{\infty }^{1}$
-AC is the union of all the
$\Sigma _{\infty }^{1}$
-AC is the union of all the
![]() $\Sigma _{n+1}^{1}$
-AC and so for the
$\Sigma _{n+1}^{1}$
-AC and so for the
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $^{-}$
versions. The variations on these principles supply us with another collection of principles that are very weak over RCA
$^{-}$
versions. The variations on these principles supply us with another collection of principles that are very weak over RCA
![]() $_{0}$
but very strong over ACA
$_{0}$
but very strong over ACA
![]() $_{0}$
. At the end we have
$_{0}$
. At the end we have
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
(and so
$^{\ast }$
(and so
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
) which have solutions produced (in a new sense) by et-forcings and for which we argue for all the properties guaranteed for
$^{-}$
) which have solutions produced (in a new sense) by et-forcings and for which we argue for all the properties guaranteed for
![]() $\Pi _{2}^{1}$
principles by Theorems 4.11–4.13. The forcing notions are quite straightforward. The argument that the property holds at the limit of even an
$\Pi _{2}^{1}$
principles by Theorems 4.11–4.13. The forcing notions are quite straightforward. The argument that the property holds at the limit of even an
![]() $\omega _{1}$
length iteration, however, needs a new twist.
$\omega _{1}$
length iteration, however, needs a new twist.
For
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
actually, there is a very simple known et-forcing that does more and requires no new ideas. The small trick is that one adds to a given countable
$^{-}$
actually, there is a very simple known et-forcing that does more and requires no new ideas. The small trick is that one adds to a given countable
![]() $\mathcal {N}\ \vDash $
RCA
$\mathcal {N}\ \vDash $
RCA
![]() $_{0}$
a generic G such that
$_{0}$
a generic G such that
![]() $\forall A\in S(\mathcal {N})(\exists i)(A=G^{[i]})$
. The conditions are just
$\forall A\in S(\mathcal {N})(\exists i)(A=G^{[i]})$
. The conditions are just
![]() $\left \langle \tau ,T\right \rangle $
with T a binary tree such that, in
$\left \langle \tau ,T\right \rangle $
with T a binary tree such that, in
![]() $\mathcal {N}$
, there is a finite set F and a sequence
$\mathcal {N}$
, there is a finite set F and a sequence
![]() $ \left \langle A_{i}|i\in F\right \rangle $
such that for
$ \left \langle A_{i}|i\in F\right \rangle $
such that for
![]() $\sigma \in T$
with
$\sigma \in T$
with
![]() $ |\sigma |>\left \langle i,n\right \rangle \geq |\tau |$
(
$ |\sigma |>\left \langle i,n\right \rangle \geq |\tau |$
(
![]() $i\in F$
and
$i\in F$
and
![]() $n\in N$
),
$n\in N$
),
![]() $\sigma (\left \langle i,n\right \rangle )=A_{i}(n)$
. Otherwise, for
$\sigma (\left \langle i,n\right \rangle )=A_{i}(n)$
. Otherwise, for
![]() $\sigma \supseteq \tau $
there are no restrictions on
$\sigma \supseteq \tau $
there are no restrictions on
![]() $\sigma \in T$
. Clearly this forcing adds a G as required. Iterating this forcing
$\sigma \in T$
. Clearly this forcing adds a G as required. Iterating this forcing
![]() $\omega _{1}$
many times gives a model
$\omega _{1}$
many times gives a model
![]() $\mathcal {N}_{\omega _{1}}$
of
$\mathcal {N}_{\omega _{1}}$
of
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
: For any instance specified by
$^{-}$
: For any instance specified by
![]() $\forall n\exists X\Phi (A,n,X)$
with
$\forall n\exists X\Phi (A,n,X)$
with
![]() $ A\in \mathcal {N}_{\omega _{1}}$
and so
$ A\in \mathcal {N}_{\omega _{1}}$
and so
![]() $A\in \mathcal {N}_{\alpha }$
for
$A\in \mathcal {N}_{\alpha }$
for
![]() $ \alpha $
countable, witness
$ \alpha $
countable, witness
![]() $X_{n}$
that
$X_{n}$
that
![]() $\exists X\Phi (n,X)$
for each n appear in some
$\exists X\Phi (n,X)$
for each n appear in some
![]() $\mathcal {N}_{\beta }$
for a countable
$\mathcal {N}_{\beta }$
for a countable
![]() $\beta $
. Thus each is a
$\beta $
. Thus each is a
![]() $G_{\beta +1}^{[k]}$
for some k as required by
$G_{\beta +1}^{[k]}$
for some k as required by
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
.
$^{-}$
.
Our proof for
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
requires more interesting twists and we present it in detail. As
$^{\ast }$
requires more interesting twists and we present it in detail. As
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
implies all of the other principles in RCA
$^{\ast }$
implies all of the other principles in RCA
![]() $_{0}$
, proving the conservation results for it implies them for the others. Thus we need not expand on the sketch just given for
$_{0}$
, proving the conservation results for it implies them for the others. Thus we need not expand on the sketch just given for
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
.
$^{-}$
.
Theorem 6.1. For
![]() $\mathcal {N}$
a countable model of RCA
$\mathcal {N}$
a countable model of RCA
![]() $_{0}$
, and any second order
$_{0}$
, and any second order
![]() $\Phi $
such that
$\Phi $
such that
![]() $\mathcal {N}\vDash \forall k\exists X\Phi (A,k,X)$
and
$\mathcal {N}\vDash \forall k\exists X\Phi (A,k,X)$
and
![]() $\mathcal {N}^{\prime }$
a countable extension of
$\mathcal {N}^{\prime }$
a countable extension of
![]() $\mathcal {N}$
satisfying RCA
$\mathcal {N}$
satisfying RCA
![]() $_{0}$
with the same first order part as
$_{0}$
with the same first order part as
![]() $\mathcal {N}$
, there is an et-forcing
$\mathcal {N}$
, there is an et-forcing
![]() $\mathcal {P}$
over
$\mathcal {P}$
over
![]() $\mathcal {N}^{\prime }$
with an appropriate collection
$\mathcal {N}^{\prime }$
with an appropriate collection
![]() $\mathcal {D}$
of dense sets such that for any
$\mathcal {D}$
of dense sets such that for any
![]() $ \mathcal {D}$
-generic G,
$ \mathcal {D}$
-generic G,
![]() $G^{[k]}\in S(\mathcal {N})$
for every
$G^{[k]}\in S(\mathcal {N})$
for every
![]() $k\in N$
and for every
$k\in N$
and for every
![]() $k\in N$
,
$k\in N$
,
![]() $\mathcal {N}\vDash \exists \sigma \Phi (A,k,G_{\sigma }^{[k]})$
.
$\mathcal {N}\vDash \exists \sigma \Phi (A,k,G_{\sigma }^{[k]})$
.
Proof Forcing conditions are like those described above for
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $ ^{-}$
but tied to
$ ^{-}$
but tied to
![]() $\Phi $
and A:
$\Phi $
and A:
![]() $\left \langle \tau ,T\right \rangle $
with
$\left \langle \tau ,T\right \rangle $
with
![]() $ T$
a binary tree such that there is, in
$ T$
a binary tree such that there is, in
![]() $\mathcal {N}$
, a finite set F and a sequence
$\mathcal {N}$
, a finite set F and a sequence
![]() $\left \langle X_{i}|i\in F\right \rangle $
such
$\left \langle X_{i}|i\in F\right \rangle $
such
![]() $\mathcal {N\vDash } \Phi (A,i,X_{i})$
for every
$\mathcal {N\vDash } \Phi (A,i,X_{i})$
for every
![]() $i\in F$
and for
$i\in F$
and for
![]() $\sigma \supseteq \tau $
and
$\sigma \supseteq \tau $
and
![]() $ |\sigma |=\left \langle i,n\right \rangle \geq |\tau |$
, if
$ |\sigma |=\left \langle i,n\right \rangle \geq |\tau |$
, if
![]() $i\in F$
,
$i\in F$
,
![]() . For other
. For other
![]() $\left \langle i,n\right \rangle $
, both
$\left \langle i,n\right \rangle $
, both
![]() and
and
![]() are in T. While this forcing is not in general definable over
are in T. While this forcing is not in general definable over
![]() $\mathcal {N} ^{\prime }$
as it refers to membership in
$\mathcal {N} ^{\prime }$
as it refers to membership in
![]() $\mathcal {N}$
, it is clearly an et-forcing over
$\mathcal {N}$
, it is clearly an et-forcing over
![]() $\mathcal {N}^{\prime }$
as each condition is in
$\mathcal {N}^{\prime }$
as each condition is in
![]() $\mathcal { N\subseteq N}^{\prime }$
and
$\mathcal { N\subseteq N}^{\prime }$
and
![]() $\sigma \in Ext(\left \langle \tau ,T\right \rangle )\Leftrightarrow \sigma \in T$
as then
$\sigma \in Ext(\left \langle \tau ,T\right \rangle )\Leftrightarrow \sigma \in T$
as then
![]() $\left \langle \sigma ,T_{\sigma }\right \rangle \leq \left \langle \tau ,T\right \rangle $
. Moreover, the sets
$\left \langle \sigma ,T_{\sigma }\right \rangle \leq \left \langle \tau ,T\right \rangle $
. Moreover, the sets
![]() $\{\left \langle \tau ,T\right \rangle |i\in F_{\left \langle \tau ,T\right \rangle }\}$
are clearly dense for each i (again even if not definable over
$\{\left \langle \tau ,T\right \rangle |i\in F_{\left \langle \tau ,T\right \rangle }\}$
are clearly dense for each i (again even if not definable over
![]() $\mathcal {N}^{\prime }$
). Thus, for any
$\mathcal {N}^{\prime }$
). Thus, for any
![]() $ \mathcal {D}$
-generic G where
$ \mathcal {D}$
-generic G where
![]() $\mathcal {D}$
includes these sets, it is clear that
$\mathcal {D}$
includes these sets, it is clear that
![]() $G^{[i]}=^{\ast }X$
for some X such that
$G^{[i]}=^{\ast }X$
for some X such that
![]() $\mathcal {N}\vDash \Phi (A,i,X)$
as required for G to satisfy the desired property.
$\mathcal {N}\vDash \Phi (A,i,X)$
as required for G to satisfy the desired property.
We now wish to iterate this theorem to produce the desired extension
![]() $ \mathcal {N}_{\omega _{1}}\vDash \Sigma _{\infty }^{1}-AC^{\ast }$
.
$ \mathcal {N}_{\omega _{1}}\vDash \Sigma _{\infty }^{1}-AC^{\ast }$
.
Theorem 6.2. If
![]() $\mathcal {N}$
is a countable model of RCA
$\mathcal {N}$
is a countable model of RCA
![]() $_{0}$
then there are extensions
$_{0}$
then there are extensions
![]() $\mathcal {N}_{\alpha }$
for
$\mathcal {N}_{\alpha }$
for
![]() $\alpha <\omega _{1}$
with the same first order part as
$\alpha <\omega _{1}$
with the same first order part as
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $\cup \{\mathcal {N}_{\alpha }|\alpha <\omega _{1}\}=\mathcal {N}_{\omega _{1}}\vDash $
RCA
$\cup \{\mathcal {N}_{\alpha }|\alpha <\omega _{1}\}=\mathcal {N}_{\omega _{1}}\vDash $
RCA
![]() $_{0}+\Sigma _{\infty }^{1}$
-AC
$_{0}+\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
generated by extensions via et-forcings which therefore omits branches (and so avoids cones). Thus
$^{\ast }$
generated by extensions via et-forcings which therefore omits branches (and so avoids cones). Thus
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
is also G-r-
$^{\ast }$
is also G-r-
![]() $\Pi _{2}^{1}$
(and so G-r-
$\Pi _{2}^{1}$
(and so G-r-
![]() $\Pi _{1}^{1}$
) conservative over RCA
$\Pi _{1}^{1}$
) conservative over RCA
![]() $_{0}$
.
$_{0}$
.
Proof We define a sequence
![]() $\mathcal {N}_{\alpha }$
,
$\mathcal {N}_{\alpha }$
,
![]() $\alpha <\omega _{1}$
of countable models of RCA
$\alpha <\omega _{1}$
of countable models of RCA
![]() $_{0}$
with the same first order part. We begin with
$_{0}$
with the same first order part. We begin with
![]() $ \mathcal {N}_{0}=\mathcal {N}$
. Given
$ \mathcal {N}_{0}=\mathcal {N}$
. Given
![]() $\mathcal {N}_{\alpha }$
we list the countably many instances given by
$\mathcal {N}_{\alpha }$
we list the countably many instances given by
![]() $A_{j}$
and
$A_{j}$
and
![]() $\Phi _{j}$
for
$\Phi _{j}$
for
![]() $j\in \omega $
such that
$j\in \omega $
such that
![]() $\mathcal {N}_{\alpha }\vDash \forall k\exists X\Phi _{j}(A_{j},k,X) $
. We then define an
$\mathcal {N}_{\alpha }\vDash \forall k\exists X\Phi _{j}(A_{j},k,X) $
. We then define an
![]() $\omega $
length iteration to construct
$\omega $
length iteration to construct
![]() $\mathcal {N}_{\alpha ,l}$
starting at
$\mathcal {N}_{\alpha ,l}$
starting at
![]() $\mathcal {N}_{a,0}=\mathcal {N}_{\alpha }$
and taking
$\mathcal {N}_{a,0}=\mathcal {N}_{\alpha }$
and taking
![]() $\mathcal {N}_{\alpha ,l+1}$
to be an extension of
$\mathcal {N}_{\alpha ,l+1}$
to be an extension of
![]() $\mathcal {N} _{\alpha ,l}$
by a generic for the forcing described above for the lth instance of
$\mathcal {N} _{\alpha ,l}$
by a generic for the forcing described above for the lth instance of
![]() $\forall n\exists X\Phi (A,n,X)$
in
$\forall n\exists X\Phi (A,n,X)$
in
![]() $\mathcal {N}_{\alpha }$
. We set
$\mathcal {N}_{\alpha }$
. We set
![]() $\mathcal {N}_{\alpha +1}=\cup \{\mathcal {N}_{\alpha ,l}|l\in \omega \}$
. As we use et-forcings, all the conditions needed for our conclusions are met along the way and at
$\mathcal {N}_{\alpha +1}=\cup \{\mathcal {N}_{\alpha ,l}|l\in \omega \}$
. As we use et-forcings, all the conditions needed for our conclusions are met along the way and at
![]() $\mathcal {N}_{\omega _{1}}=\cup \{\mathcal {N}_{\alpha }|\alpha <\omega _{1}\}$
.
$\mathcal {N}_{\omega _{1}}=\cup \{\mathcal {N}_{\alpha }|\alpha <\omega _{1}\}$
.
All that needs to be verified here beyond what was done for
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
is that
$^{\ast }$
is that
![]() $\mathcal {N}_{\omega _{1}}\vDash \Sigma _{\infty }^{1}$
-AC
$\mathcal {N}_{\omega _{1}}\vDash \Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
. The crucial fact here is that the
$^{\ast }$
. The crucial fact here is that the
![]() $\alpha $
such that
$\alpha $
such that
![]() $ \mathcal {N}_{\alpha }$
is an elementary submodel of
$ \mathcal {N}_{\alpha }$
is an elementary submodel of
![]() $\mathcal {N}_{\omega _{1}}$
(in the full second order language) include a closed unbounded set. With this in mind, consider any
$\mathcal {N}_{\omega _{1}}$
(in the full second order language) include a closed unbounded set. With this in mind, consider any
![]() $A\in \mathcal {N}_{\omega _{1}}$
and
$A\in \mathcal {N}_{\omega _{1}}$
and
![]() $\Phi (A,n,X)$
such that
$\Phi (A,n,X)$
such that
![]() $\mathcal {N}_{\omega _{1}}\vDash \forall n\exists X\Phi (A,n,X)$
. Take an
$\mathcal {N}_{\omega _{1}}\vDash \forall n\exists X\Phi (A,n,X)$
. Take an
![]() $\alpha $
such that
$\alpha $
such that
![]() $A\in \mathcal {N}_{\alpha }$
which is an elementary submodel of
$A\in \mathcal {N}_{\alpha }$
which is an elementary submodel of
![]() $\mathcal {N}_{\omega _{1}}$
and so also satisfies
$\mathcal {N}_{\omega _{1}}$
and so also satisfies
![]() $ \forall n\exists X\Phi (A,n,X)$
. Our construction therefore guarantees that there is an l and a
$ \forall n\exists X\Phi (A,n,X)$
. Our construction therefore guarantees that there is an l and a
![]() $Z\in \mathcal {N}_{\alpha ,l}$
so that for every
$Z\in \mathcal {N}_{\alpha ,l}$
so that for every
![]() $n\in N$
,
$n\in N$
,
![]() $Z^{[n]}\in \mathcal {N}_{\alpha }$
and
$Z^{[n]}\in \mathcal {N}_{\alpha }$
and
![]() $\mathcal {N}_{\alpha }\vDash \exists \sigma \Phi (A,n,Z_{\sigma }^{[n]})$
. As
$\mathcal {N}_{\alpha }\vDash \exists \sigma \Phi (A,n,Z_{\sigma }^{[n]})$
. As
![]() $A,Z\in \mathcal {N}_{\omega _{1}}$
which is an elementary extension of
$A,Z\in \mathcal {N}_{\omega _{1}}$
which is an elementary extension of
![]() $\mathcal {N}_{\alpha }$
, we now have that
$\mathcal {N}_{\alpha }$
, we now have that
![]() $\mathcal {N}_{\omega _{1}}\vDash \exists \sigma \Phi (A,n,Z_{\sigma }^{[n]})$
for every
$\mathcal {N}_{\omega _{1}}\vDash \exists \sigma \Phi (A,n,Z_{\sigma }^{[n]})$
for every
![]() $n\in N$
and so
$n\in N$
and so
![]() $\mathcal {N}_{\omega _{1}}\vDash \exists Z\forall n\exists \sigma \Phi (A,n,Z_{\sigma }^{[n]})$
as required.
$\mathcal {N}_{\omega _{1}}\vDash \exists Z\forall n\exists \sigma \Phi (A,n,Z_{\sigma }^{[n]})$
as required.
Theorem 6.3. For each
![]() $n\in \omega $
, ACA
$n\in \omega $
, ACA
![]() $_{0}\vdash \Sigma _{n+2}^{1}$
-AC
$_{0}\vdash \Sigma _{n+2}^{1}$
-AC
![]() $ ^{\ast }\rightarrow \Sigma _{n+2}^{1}$
-AC
$ ^{\ast }\rightarrow \Sigma _{n+2}^{1}$
-AC
![]() $^{-}\rightarrow \Sigma _{n+1}^{1}$
-CA
$^{-}\rightarrow \Sigma _{n+1}^{1}$
-CA
![]() $_{0}$
and so ACA
$_{0}$
and so ACA
![]() $_{0}\vdash \Sigma _{\infty }^{1}$
-AC
$_{0}\vdash \Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }\rightarrow \Sigma _{\infty }^{1}$
-AC
$^{\ast }\rightarrow \Sigma _{\infty }^{1}$
-AC
![]() $^{-}\rightarrow \Sigma _{n+1}^{1}$
-CA
$^{-}\rightarrow \Sigma _{n+1}^{1}$
-CA
![]() $ _{0}$
.
$ _{0}$
.
Proof The implication
![]() $\Sigma _{n+2}^{1}$
-AC
$\Sigma _{n+2}^{1}$
-AC
![]() $^{\ast }\rightarrow \Sigma _{n+2}^{1}$
-AC
$^{\ast }\rightarrow \Sigma _{n+2}^{1}$
-AC
![]() $^{-}$
is Proposition 5.4. We prove
$^{-}$
is Proposition 5.4. We prove
![]() $\Sigma _{n+2}^{1}$
-AC
$\Sigma _{n+2}^{1}$
-AC
![]() $ ^{-}\rightarrow \Sigma _{n+1}^{1}$
-CA
$ ^{-}\rightarrow \Sigma _{n+1}^{1}$
-CA
![]() $_{0}$
in ACA
$_{0}$
in ACA
![]() $_{0}$
by induction on n. Consider
$_{0}$
by induction on n. Consider
![]() $\exists X\Psi (k,X)$
for a
$\exists X\Psi (k,X)$
for a
![]() $\Pi _{n}^{1}$
formula
$\Pi _{n}^{1}$
formula
![]() $\Psi $
(
$\Psi $
(
![]() $\Pi _{0}^{1}$
is arithmetic). We want to prove that there is a set
$\Pi _{0}^{1}$
is arithmetic). We want to prove that there is a set
![]() $ R=\{k|\exists X\Psi (k,X)\}$
. Define
$ R=\{k|\exists X\Psi (k,X)\}$
. Define
![]() $\Phi (k,X)$
as
$\Phi (k,X)$
as
![]() $\Psi (k,X)~\vee ~(X=\emptyset \wedge \lnot \exists Y\psi (k,Y))$
. Clearly
$\Psi (k,X)~\vee ~(X=\emptyset \wedge \lnot \exists Y\psi (k,Y))$
. Clearly
![]() $\Phi $
is
$\Phi $
is
![]() $\Pi _{n+1}^{1}$
and
$\Pi _{n+1}^{1}$
and
![]() $\forall k\exists X\Phi (k,X)$
. Thus we may apply
$\forall k\exists X\Phi (k,X)$
. Thus we may apply
![]() $\Sigma _{n+2}^{1}$
-AC
$\Sigma _{n+2}^{1}$
-AC
![]() $^{-}$
to get a set Z such that
$^{-}$
to get a set Z such that
![]() $\forall k\exists m\Phi (k,Z^{[m]})$
. Thus
$\forall k\exists m\Phi (k,Z^{[m]})$
. Thus
![]() $k\in R\Leftrightarrow \exists X\Psi (k,X)\Leftrightarrow \exists m\Psi (k,Z^{[m]})$
. Now
$k\in R\Leftrightarrow \exists X\Psi (k,X)\Leftrightarrow \exists m\Psi (k,Z^{[m]})$
. Now
![]() $S=\{\left \langle k,m\right \rangle |\Psi (k,Z^{[m]})\}$
is
$S=\{\left \langle k,m\right \rangle |\Psi (k,Z^{[m]})\}$
is
![]() $\Pi _{n}^{1}$
and so exists by induction. (For
$\Pi _{n}^{1}$
and so exists by induction. (For
![]() $n=0$
this is ACA
$n=0$
this is ACA
![]() $_{0}$
.) And so
$_{0}$
.) And so
![]() $R=\{k|\exists m(\left \langle k,m\right \rangle \in S\}$
exists by ACA
$R=\{k|\exists m(\left \langle k,m\right \rangle \in S\}$
exists by ACA
![]() $_{0}$
.
$_{0}$
.
Thus we have whole hierarchies of principles that are very weak over RCA
![]() $ _{0} $
but very strong over ACA
$ _{0} $
but very strong over ACA
![]() $_{0}$
and indeed equivalent to a hierarchy of standard systems. At the end,
$_{0}$
and indeed equivalent to a hierarchy of standard systems. At the end,
![]() $\Sigma _{\infty }^{1}-AC^{\ast }$
and
$\Sigma _{\infty }^{1}-AC^{\ast }$
and
![]() $ \Sigma _{\infty }^{1}$
-AC
$ \Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
are G-r-
$^{-}$
are G-r-
![]() $\Pi _{2}^{1}$
conservative over RCA
$\Pi _{2}^{1}$
conservative over RCA
![]() $ _{0}$
with extensions omitting branches but, over ACA
$ _{0}$
with extensions omitting branches but, over ACA
![]() $_{0}$
, are both equivalent to
$_{0}$
, are both equivalent to
![]() $\Sigma _{\infty }^{1}-AC_{\infty }$
and so strictly stronger than full second order arithmetic (Feferman and Levy; see [Reference Simpson28, Remark VII.6.3]). We view these results and the ones on ATHAs that are equivalent to known THAs over ACA
$\Sigma _{\infty }^{1}-AC_{\infty }$
and so strictly stronger than full second order arithmetic (Feferman and Levy; see [Reference Simpson28, Remark VII.6.3]). We view these results and the ones on ATHAs that are equivalent to known THAs over ACA
![]() $_{0}$
as supplying answers to the question raised by Hirschfeldt and repeated in [Reference Montalbán22] by providing an ample list of many pairs of principles that are very different over RCA
$_{0}$
as supplying answers to the question raised by Hirschfeldt and repeated in [Reference Montalbán22] by providing an ample list of many pairs of principles that are very different over RCA
![]() $_{0}$
but equivalent over ACA
$_{0}$
but equivalent over ACA
![]() $_{0}$
. It could well be argued that these weak ones should really be seen as the same as their strong counterparts in an analysis that works over ACA
$_{0}$
. It could well be argued that these weak ones should really be seen as the same as their strong counterparts in an analysis that works over ACA
![]() $_{0}$
rather than RCA
$_{0}$
rather than RCA
![]() $_{0}$
.
$_{0}$
.
7 Tanaka conservativity
We close with some words about earlier work on the collection axioms (
![]() $ \Sigma _{n}^{1}$
-AC
$ \Sigma _{n}^{1}$
-AC
![]() $^{-}$
and
$^{-}$
and
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
) and another type of conservation result that was brought to our attention by this work which applies to all the principles we have investigated here.
$^{-}$
) and another type of conservation result that was brought to our attention by this work which applies to all the principles we have investigated here.
The work by Tanaka, Montalbán, and Yamazaki on conservativity of
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
(or as they call it,
$^{-}$
(or as they call it,
![]() $\Pi _{\infty }^{1}$
collection) over RCA
$\Pi _{\infty }^{1}$
collection) over RCA
![]() $_{0}$
has, far as we have determined, never been published. The only source I have access to is a set of slides from a talk by Yamazaki [Reference Yamazaki33] sent to me by Keita Yokoyama. Based on those slides, the methods used seem considerably more complicated than the ones presented here. In particular, to prove
$_{0}$
has, far as we have determined, never been published. The only source I have access to is a set of slides from a talk by Yamazaki [Reference Yamazaki33] sent to me by Keita Yokoyama. Based on those slides, the methods used seem considerably more complicated than the ones presented here. In particular, to prove
![]() $\Pi _{1}^{1}$
conservativity they seem to restrict attention to principle models of RCA
$\Pi _{1}^{1}$
conservativity they seem to restrict attention to principle models of RCA
![]() $_{0}$
(ones with a single set such that every set in the model is recursive in it) and use both
$_{0}$
(ones with a single set such that every set in the model is recursive in it) and use both
![]() $\Pi _{1}^{0}$
forcing (i.e., infinite binary trees recursive in a single set) and forcing with uniformly pointed perfect trees along with
$\Pi _{1}^{0}$
forcing (i.e., infinite binary trees recursive in a single set) and forcing with uniformly pointed perfect trees along with
![]() $\omega _{1}$
iterations. (Of course, the slides just outline proofs at best.)
$\omega _{1}$
iterations. (Of course, the slides just outline proofs at best.)
Our proofs, certainly for
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
and, I would say, even for
$^{-}$
and, I would say, even for
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
, are much simpler. Yamazaki does get more by including WKL
$^{\ast }$
, are much simpler. Yamazaki does get more by including WKL
![]() $_{0}$
as well (and so the use of
$_{0}$
as well (and so the use of
![]() $\Pi _{1}^{0} $
forcing makes sense). We have already pointed out that for
$\Pi _{1}^{0} $
forcing makes sense). We have already pointed out that for
![]() $\Pi _{1}^{1}$
conservativity, we can easily add solutions to WKL to our constructions with its own forcing notion (with
$\Pi _{1}^{1}$
conservativity, we can easily add solutions to WKL to our constructions with its own forcing notion (with
![]() $\Pi _{1}^{0}$
classes) to get this
$\Pi _{1}^{0}$
classes) to get this
![]() $\Pi _{1}^{1}$
conservativity result and the same one for
$\Pi _{1}^{1}$
conservativity result and the same one for
![]() $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
. Yamazaki does not consider r-
$^{\ast }$
. Yamazaki does not consider r-
![]() $\Pi _{2}^{1}$
conservativity although he does present an analog of minimal pairs for models of WKL
$\Pi _{2}^{1}$
conservativity although he does present an analog of minimal pairs for models of WKL
![]() $_{0}$
from [Reference Simpson, Tanaka and Yamazaki29]. They are used in STY even in their proof of
$_{0}$
from [Reference Simpson, Tanaka and Yamazaki29]. They are used in STY even in their proof of
![]() $\Pi _{1}^{1}$
conservativity. I expect this analysis was motivated in the same way as in STY by the desire to prove a different kind of conservativity over RCA
$\Pi _{1}^{1}$
conservativity. I expect this analysis was motivated in the same way as in STY by the desire to prove a different kind of conservativity over RCA
![]() $_{0}$
conjectured for WKL
$_{0}$
conjectured for WKL
![]() $_{0}$
by Tanaka and proved in STY. We establish this conservation result for
$_{0}$
by Tanaka and proved in STY. We establish this conservation result for
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
and indeed for all principles we have analyzed using forcing. Moreover, we prove both a generalization of Tanaka conservativity analogous to our generalization for
$^{\ast }$
and indeed for all principles we have analyzed using forcing. Moreover, we prove both a generalization of Tanaka conservativity analogous to our generalization for
![]() $\Pi _{1}^{1}$
conservativity (Definition 4.9 and Theorem 4.11) and a more inclusive variation analogous to our generalization of r-
$\Pi _{1}^{1}$
conservativity (Definition 4.9 and Theorem 4.11) and a more inclusive variation analogous to our generalization of r-
![]() $\Pi _{2}^{1}$
conservativity (Definition 4.10 and Theorem 4.12). (This one fails for WKL as for the previously mentioned r-
$\Pi _{2}^{1}$
conservativity (Definition 4.10 and Theorem 4.12). (This one fails for WKL as for the previously mentioned r-
![]() $\Pi _{2}^{1}$
conservativity as it is more general.)
$\Pi _{2}^{1}$
conservativity as it is more general.)
Definition 7.1.
Tanaka conservativity means conservativity for all sentences of the form
![]() $\forall X\exists !Y\Phi (X,Y)$
for arithmetic
$\forall X\exists !Y\Phi (X,Y)$
for arithmetic
![]() $\Phi $
. We define G-Tanaka conservativity to be conservativity for sentences in the class of G-Tanaka formulas which are formed by closing the quantifier free formulas and those of the form
$\Phi $
. We define G-Tanaka conservativity to be conservativity for sentences in the class of G-Tanaka formulas which are formed by closing the quantifier free formulas and those of the form
![]() $\exists !Y\Phi (Y)$
for arithmetic
$\exists !Y\Phi (Y)$
for arithmetic
![]() $\Phi $
under the same operations as for G-
$\Phi $
under the same operations as for G-
![]() $\Pi _{1}^{1}$
in Definition 4.9 (
$\Pi _{1}^{1}$
in Definition 4.9 (
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
,
$\vee $
,
![]() $\forall x$
,
$\forall x$
,
![]() $\exists x$
, and
$\exists x$
, and
![]() $\forall X$
). We define the G-r-Tanaka formulasas we did the G-Tanaka ones but including formulas of the form
$\forall X$
). We define the G-r-Tanaka formulasas we did the G-Tanaka ones but including formulas of the form
![]() $\exists !Y\exists Z\Psi ( \bar {x},Y,Z)$
with
$\exists !Y\exists Z\Psi ( \bar {x},Y,Z)$
with
![]() $\Psi $
a
$\Psi $
a
![]() $\Sigma _{3}^{0}$
formula in the base class of formulas (and then closing under
$\Sigma _{3}^{0}$
formula in the base class of formulas (and then closing under
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
,
$\vee $
,
![]() $\forall x$
,
$\forall x$
,
![]() $\exists x$
, and
$\exists x$
, and
![]() $\forall X$
). G-r-Tanaka conservativity is then defined as usual.
$\forall X$
). G-r-Tanaka conservativity is then defined as usual.
Remark 7.2. Tanaka conservativity was called
![]() $\mathfrak {Uniq}$
conservativity in [Reference Yamazaki34]. He studied it primarily for
$\mathfrak {Uniq}$
conservativity in [Reference Yamazaki34]. He studied it primarily for
![]() $\Pi _{2}^{1}$
principles including WKL, COH, RCA
$\Pi _{2}^{1}$
principles including WKL, COH, RCA
![]() $^{+}$
(or
$^{+}$
(or
![]() $\Pi _{\infty }^{1}$
G) over RCA
$\Pi _{\infty }^{1}$
G) over RCA
![]() $_{0}$
+ I
$_{0}$
+ I
![]() $ \Sigma _{n}^{0}$
and he cites earlier work of Kihara [Reference Kihara18] on COH and Yamazaki [Reference Yamazaki32] on RCA
$ \Sigma _{n}^{0}$
and he cites earlier work of Kihara [Reference Kihara18] on COH and Yamazaki [Reference Yamazaki32] on RCA
![]() $^{+}$
and unpublished work on COH. We thank Yokoyama for these references as well.
$^{+}$
and unpublished work on COH. We thank Yokoyama for these references as well.
It is clear that G-r-Tanaka conservativity includes all the other versions defined here as well as those in Section 4. We prove these conservativity results by isolating one extra property of et-forcings needed to carry out the proof and note that the et-forcings used for our
![]() $\Sigma _{\infty }^{1}-AC^{\ast }$
results as well as all the others in this paper have this property. The idea is that for any condition
$\Sigma _{\infty }^{1}-AC^{\ast }$
results as well as all the others in this paper have this property. The idea is that for any condition
![]() $\left \langle \tau ,T\right \rangle $
the subtrees above any two
$\left \langle \tau ,T\right \rangle $
the subtrees above any two
![]() $\rho ,\sigma \in T$
of the same length look the same. Although stronger or simpler restrictions can be given that fit most of our examples, we formulate “look the same” in a fairly general way that matches our overall approach to et-forcings yet is strong enough to eliminate some technical problems.
$\rho ,\sigma \in T$
of the same length look the same. Although stronger or simpler restrictions can be given that fit most of our examples, we formulate “look the same” in a fairly general way that matches our overall approach to et-forcings yet is strong enough to eliminate some technical problems.
Definition 7.3. An et-forcing
![]() $\mathcal {P}$
is uniform (a uet-forcing) if, for every condition
$\mathcal {P}$
is uniform (a uet-forcing) if, for every condition
![]() $\left \langle \tau ,T\right \rangle $
, every
$\left \langle \tau ,T\right \rangle $
, every
![]() $\rho ,\sigma \in Ext(\left \langle \tau ,T\right \rangle )$
with
$\rho ,\sigma \in Ext(\left \langle \tau ,T\right \rangle )$
with
![]() $|\rho |=|\sigma |$
, and every
$|\rho |=|\sigma |$
, and every
![]() $\left \langle \rho ^{\prime \prime },R^{\prime \prime }\right \rangle \leq \left \langle \rho ^{\prime },R^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
with
$\left \langle \rho ^{\prime \prime },R^{\prime \prime }\right \rangle \leq \left \langle \rho ^{\prime },R^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
with
![]() $\rho \subseteq \rho ^{\prime } $
,
$\rho \subseteq \rho ^{\prime } $
,
![]() $\left \langle \rho _{\sigma }^{\prime \prime },R_{\sigma }^{\prime \prime }\right \rangle \leq \left \langle \rho _{\sigma }^{\prime },R_{\sigma }^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
. (Of course, then
$\left \langle \rho _{\sigma }^{\prime \prime },R_{\sigma }^{\prime \prime }\right \rangle \leq \left \langle \rho _{\sigma }^{\prime },R_{\sigma }^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
. (Of course, then
![]() $\sigma \subseteq \rho _{\sigma }^{\prime }$
.) As a technical convenience we add on another condition that clearly cannot change the results of a forcing construction: If
$\sigma \subseteq \rho _{\sigma }^{\prime }$
.) As a technical convenience we add on another condition that clearly cannot change the results of a forcing construction: If
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {P}$
and the stem of T is some
$\left \langle \tau ,T\right \rangle \in \mathcal {P}$
and the stem of T is some
![]() $\sigma \supset \tau $
then
$\sigma \supset \tau $
then
![]() $ \left \langle \rho ,T\right \rangle \leq \left \langle \tau ,T\right \rangle $
whenever
$ \left \langle \rho ,T\right \rangle \leq \left \langle \tau ,T\right \rangle $
whenever
![]() $\sigma \supseteq \rho \supseteq \tau $
.
$\sigma \supseteq \rho \supseteq \tau $
.
The crucial lemma that we need about uet-forcings is the following:
Lemma 7.4. Suppose
![]() $\mathcal {P}$
is a uet-forcing (over a countable
$\mathcal {P}$
is a uet-forcing (over a countable
![]() $ \mathcal {N}\vDash $
RCA
$ \mathcal {N}\vDash $
RCA
![]() $_{0}$
) and
$_{0}$
) and
![]() $\mathcal {D}$
is a countable collection of dense sets. We can extend
$\mathcal {D}$
is a countable collection of dense sets. We can extend
![]() $\mathcal {D}$
to another countable collection of dense sets
$\mathcal {D}$
to another countable collection of dense sets
![]() $\mathcal {D}^{\prime }$
such that for any
$\mathcal {D}^{\prime }$
such that for any
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {P}$
,
$\left \langle \tau ,T\right \rangle \in \mathcal {P}$
,
![]() $\rho ,\sigma \in Ext(\left \langle \tau ,T\right \rangle )$
of the same length and
$\rho ,\sigma \in Ext(\left \langle \tau ,T\right \rangle )$
of the same length and
![]() $\mathcal {D}^{\prime }$
-generic
$\mathcal {D}^{\prime }$
-generic
![]() $ G\supseteq \rho $
whose generic filter contains
$ G\supseteq \rho $
whose generic filter contains
![]() $\left \langle \tau ,T\right \rangle $
,
$\left \langle \tau ,T\right \rangle $
,
![]() $G_{\sigma }$
is
$G_{\sigma }$
is
![]() $\mathcal {D}$
-generic.
$\mathcal {D}$
-generic.
Proof We want to guarantee that for any
![]() $G\supseteq \rho $
with a
$G\supseteq \rho $
with a
![]() $\mathcal {D} ^{\prime }$
-generic sequence
$\mathcal {D} ^{\prime }$
-generic sequence
![]() $\left \langle \rho ^{i},R^{i}\right \rangle $
(i.e., for each
$\left \langle \rho ^{i},R^{i}\right \rangle $
(i.e., for each
![]() $D^{\prime }\in \mathcal {D}^{\prime }$
, there is an i such that
$D^{\prime }\in \mathcal {D}^{\prime }$
, there is an i such that
![]() $\left \langle \rho ^{i},R^{i}\right \rangle \in D^{\prime }$
) all extending
$\left \langle \rho ^{i},R^{i}\right \rangle \in D^{\prime }$
) all extending
![]() $\left \langle \tau ,T\right \rangle $
and wlog
$\left \langle \tau ,T\right \rangle $
and wlog
![]() $ \rho ^{i}\supseteq \rho $
,
$ \rho ^{i}\supseteq \rho $
,
![]() $\left \langle \rho _{\sigma }^{i},R_{\sigma }^{i}\right \rangle $
is a
$\left \langle \rho _{\sigma }^{i},R_{\sigma }^{i}\right \rangle $
is a
![]() $\mathcal {D}$
-generic sequence. It is a decreasing sequence of conditions all extending
$\mathcal {D}$
-generic sequence. It is a decreasing sequence of conditions all extending
![]() $\left \langle \tau ,T\right \rangle $
by uniformity. Of course, its generic (
$\left \langle \tau ,T\right \rangle $
by uniformity. Of course, its generic (
![]() $\cup \rho _{\sigma }^{i}$
) is
$\cup \rho _{\sigma }^{i}$
) is
![]() $ G_{\sigma }$
as required. Consider then any
$ G_{\sigma }$
as required. Consider then any
![]() $D\in \mathcal {D}$
. We want an
$D\in \mathcal {D}$
. We want an
![]() $ m $
such that
$ m $
such that
![]() $\left \langle \rho _{\sigma }^{m},R_{\sigma }^{m}\right \rangle \in D$
. We define a
$\left \langle \rho _{\sigma }^{m},R_{\sigma }^{m}\right \rangle \in D$
. We define a
![]() $D^{\prime }$
by removing all
$D^{\prime }$
by removing all
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \rho ^{0},R^{0}\right \rangle $
from D and adding in
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \rho ^{0},R^{0}\right \rangle $
from D and adding in
![]() $\left \langle \tau _{\rho }^{\prime },T_{\rho }^{\prime }\right \rangle $
for each
$\left \langle \tau _{\rho }^{\prime },T_{\rho }^{\prime }\right \rangle $
for each
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \rho _{\sigma }^{0},R_{\sigma }^{0}\right \rangle $
in D.
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \rho _{\sigma }^{0},R_{\sigma }^{0}\right \rangle $
in D.
Now if
![]() $D^{\prime }$
is dense we can put it into
$D^{\prime }$
is dense we can put it into
![]() $\mathcal {D}^{\prime }$
. On this assumption, we have an m such that
$\mathcal {D}^{\prime }$
. On this assumption, we have an m such that
![]() $\left \langle \rho ^{m},R^{m}\right \rangle =\left \langle \tau _{\rho }^{\prime },T_{\rho }^{\prime }\right \rangle $
for some
$\left \langle \rho ^{m},R^{m}\right \rangle =\left \langle \tau _{\rho }^{\prime },T_{\rho }^{\prime }\right \rangle $
for some
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \rho _{\sigma }^{0},R_{\sigma }^{0}\right \rangle $
in D. Now
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \rho _{\sigma }^{0},R_{\sigma }^{0}\right \rangle $
in D. Now
![]() $\left \langle \rho _{\sigma }^{m},R_{\sigma }^{m}\right \rangle =\left \langle (\tau _{\rho }^{\prime })_{\sigma },(T_{\rho }^{\prime })_{\sigma }\right \rangle =\left \langle \tau ^{\prime },T^{\prime }\right \rangle \in D$
as required. (Note that
$\left \langle \rho _{\sigma }^{m},R_{\sigma }^{m}\right \rangle =\left \langle (\tau _{\rho }^{\prime })_{\sigma },(T_{\rho }^{\prime })_{\sigma }\right \rangle =\left \langle \tau ^{\prime },T^{\prime }\right \rangle \in D$
as required. (Note that
![]() $\tau ^{\prime }\supseteq \rho _{\sigma }^{0}\supseteq \sigma $
so
$\tau ^{\prime }\supseteq \rho _{\sigma }^{0}\supseteq \sigma $
so
![]() $(\tau _{\rho }^{\prime })_{\sigma }=\tau ^{\prime }$
as
$(\tau _{\rho }^{\prime })_{\sigma }=\tau ^{\prime }$
as
![]() $|\sigma |=\left \vert \rho \right \vert $
.)
$|\sigma |=\left \vert \rho \right \vert $
.)
All that remains is to prove that each such
![]() $D^{\prime }$
is dense. Consider any
$D^{\prime }$
is dense. Consider any
![]() $\left \langle \tau ,T\right \rangle $
. If it is incompatible with
$\left \langle \tau ,T\right \rangle $
. If it is incompatible with
![]() $ \left \langle \rho ^{0},R^{0}\right \rangle $
then any extension in D is in
$ \left \langle \rho ^{0},R^{0}\right \rangle $
then any extension in D is in
![]() $ D^{\prime }$
. Otherwise we have a
$ D^{\prime }$
. Otherwise we have a
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle $
extending both. By uniformity,
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle $
extending both. By uniformity,
![]() $\left \langle \tau _{\sigma }^{\prime },T_{\sigma }^{\prime }\right \rangle \leq \left \langle \rho _{\sigma }^{0},R_{\sigma }^{0}\right \rangle $
. By the density of D we have a
$\left \langle \tau _{\sigma }^{\prime },T_{\sigma }^{\prime }\right \rangle \leq \left \langle \rho _{\sigma }^{0},R_{\sigma }^{0}\right \rangle $
. By the density of D we have a
![]() $\left \langle \tau ^{\prime \prime },T^{\prime \prime }\right \rangle \leq \left \langle \tau _{\sigma }^{\prime },T_{\sigma }^{\prime }\right \rangle $
in D. So by uniformity again,
$\left \langle \tau ^{\prime \prime },T^{\prime \prime }\right \rangle \leq \left \langle \tau _{\sigma }^{\prime },T_{\sigma }^{\prime }\right \rangle $
in D. So by uniformity again,
![]() $\left \langle \tau _{\rho }^{\prime \prime },T_{\rho }^{\prime \prime }\right \rangle \leq \left \langle (\tau _{\sigma }^{\prime })_{\rho },(T_{\sigma }^{\prime })_{\rho }\right \rangle =\left \langle \tau ^{\prime },T^{\prime }\right \rangle $
as required.
$\left \langle \tau _{\rho }^{\prime \prime },T_{\rho }^{\prime \prime }\right \rangle \leq \left \langle (\tau _{\sigma }^{\prime })_{\rho },(T_{\sigma }^{\prime })_{\rho }\right \rangle =\left \langle \tau ^{\prime },T^{\prime }\right \rangle $
as required.
Up until now we have not needed more about forcing than the starting level for
![]() $\Sigma _{1}^{0}$
sentences. For Theorem 7.5 we need to be able to handle all arithmetic sentences. Rather than try to give formal definitions for models
$\Sigma _{1}^{0}$
sentences. For Theorem 7.5 we need to be able to handle all arithmetic sentences. Rather than try to give formal definitions for models
![]() $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
![]() $_{0}$
(of which there are several in the literature of reverse mathematics) we just note the relevant properties. Typically one considers forcings which are at least definable. While most of the ones we have used are definable, the one for
$_{0}$
(of which there are several in the literature of reverse mathematics) we just note the relevant properties. Typically one considers forcings which are at least definable. While most of the ones we have used are definable, the one for
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
was not. Now one can make due with definable forcings there by at every even stage or limit stage
$^{\ast }$
was not. Now one can make due with definable forcings there by at every even stage or limit stage
![]() $\lambda $
first using the forcing defined for
$\lambda $
first using the forcing defined for
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{-}$
that makes every
$^{-}$
that makes every
![]() $A\in \mathcal {N}_{\lambda }$
a column of
$A\in \mathcal {N}_{\lambda }$
a column of
![]() $G_{\lambda +1}$
. Then one can define the forcing we wanted to use at each successor stage for
$G_{\lambda +1}$
. Then one can define the forcing we wanted to use at each successor stage for
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $^{\ast }$
for the
$^{\ast }$
for the
![]() $G_{\lambda +n+2}$
and defining the forcing over
$G_{\lambda +n+2}$
and defining the forcing over
![]() $ \mathcal {N}_{\lambda +n+1}$
where one can quantify over sets in
$ \mathcal {N}_{\lambda +n+1}$
where one can quantify over sets in
![]() $\mathcal {N} _{\lambda }$
by using
$\mathcal {N} _{\lambda }$
by using
![]() $G_{\lambda +1}$
as a parameter. However, we claim that this is not really necessary to get the required properties of forcing. What we want to know is that we can define the forcing relation
$G_{\lambda +1}$
as a parameter. However, we claim that this is not really necessary to get the required properties of forcing. What we want to know is that we can define the forcing relation
![]() $ \left \langle \tau ,T\right \rangle \Vdash \Theta $
starting at the
$ \left \langle \tau ,T\right \rangle \Vdash \Theta $
starting at the
![]() $\Sigma _{1}^{0}$
level as before so that there it depends only on the
$\Sigma _{1}^{0}$
level as before so that there it depends only on the
![]() $\tau $
in our conditions
$\tau $
in our conditions
![]() $\left \langle \tau ,T\right \rangle $
in
$\left \langle \tau ,T\right \rangle $
in
![]() $\mathcal {N}$
and implies truth for all extensions of
$\mathcal {N}$
and implies truth for all extensions of
![]() $\tau $
. (This level includes what we have already assumed about members of
$\tau $
. (This level includes what we have already assumed about members of
![]() $\mathcal {N}[G]$
being of a form that we think of as
$\mathcal {N}[G]$
being of a form that we think of as
![]() $\Phi _{e}^{A\oplus G}$
for
$\Phi _{e}^{A\oplus G}$
for
![]() $e\in N$
and
$e\in N$
and
![]() $A\in S(\mathcal {N})$
in a way that only relies on the initial segments
$A\in S(\mathcal {N})$
in a way that only relies on the initial segments
![]() $\tau $
of G in the conditions in the generic filter.) We can then continue on up the arithmetic hierarchy so as to guarantee the density of conditions deciding each sentence and forcing equals truth for all sufficiently generic sets. (So for G generic,
$\tau $
of G in the conditions in the generic filter.) We can then continue on up the arithmetic hierarchy so as to guarantee the density of conditions deciding each sentence and forcing equals truth for all sufficiently generic sets. (So for G generic,
![]() $\mathcal {N}[G]\vDash \Theta $
if and only if there is a condition
$\mathcal {N}[G]\vDash \Theta $
if and only if there is a condition
![]() $\left \langle \tau ,T\right \rangle $
in the generic filter such that
$\left \langle \tau ,T\right \rangle $
in the generic filter such that
![]() $\left \langle \tau ,T\right \rangle \Vdash \Theta $
.) We are not concerned with the level of the definability of the forcing relation (or even with the notions being definable over
$\left \langle \tau ,T\right \rangle \Vdash \Theta $
.) We are not concerned with the level of the definability of the forcing relation (or even with the notions being definable over
![]() $\mathcal {N}$
at all).
$\mathcal {N}$
at all).
If one wanted to be more specific, we would deal only with prenex normal sentences and take negation to be a shorthand for the prenex normal equivalent of the negation of the given sentence. At the
![]() $\Pi _{1}^{0}$
level we explicitly define
$\Pi _{1}^{0}$
level we explicitly define
![]() $\left \langle \tau ,T\right \rangle \Vdash \forall x\Phi (x,G)$
as there being no
$\left \langle \tau ,T\right \rangle \Vdash \forall x\Phi (x,G)$
as there being no
![]() $\sigma \in Ext(\left \langle \tau ,T\right \rangle )$
and no n such that
$\sigma \in Ext(\left \langle \tau ,T\right \rangle )$
and no n such that
![]() $\sigma \Vdash \lnot \Phi (n,G)$
. We then proceed by induction on the number of quantifiers in our prenex normal
$\sigma \Vdash \lnot \Phi (n,G)$
. We then proceed by induction on the number of quantifiers in our prenex normal
![]() $ \Phi $
as usual:
$ \Phi $
as usual:
![]() $\left \langle \tau ,T\right \rangle \Vdash \exists x\Psi (x,G)$
if
$\left \langle \tau ,T\right \rangle \Vdash \exists x\Psi (x,G)$
if
![]() $\left \langle \tau ,T\right \rangle \Vdash \Psi (n,G)$
for some n;
$\left \langle \tau ,T\right \rangle \Vdash \Psi (n,G)$
for some n;
![]() $\left \langle \tau ,T\right \rangle \Vdash \forall x\Psi (x,G)$
if there is no
$\left \langle \tau ,T\right \rangle \Vdash \forall x\Psi (x,G)$
if there is no
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
and no n such that
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
and no n such that
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \Vdash \lnot \Psi (n,G)$
. In any case, there are countably many dense sets that guarantee the every arithmetic sentence about G (with parameters from the ground model
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \Vdash \lnot \Psi (n,G)$
. In any case, there are countably many dense sets that guarantee the every arithmetic sentence about G (with parameters from the ground model
![]() $\mathcal {N}$
) or its negation is forced and that being forced is equivalent to the sentence being true in the generic extension. We assume that all generics in the rest of this section are generic for all these dense sets as well as the ones of Theorems 4.5.1 and 4.5.2 for all trees in
$\mathcal {N}$
) or its negation is forced and that being forced is equivalent to the sentence being true in the generic extension. We assume that all generics in the rest of this section are generic for all these dense sets as well as the ones of Theorems 4.5.1 and 4.5.2 for all trees in
![]() $\mathcal {N}$
with no branches in
$\mathcal {N}$
with no branches in
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
We can now state the main property need for our conservation results.
Theorem 7.5. For any countable model
![]() $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
![]() $_{0}$
and any extension
$_{0}$
and any extension
![]() $\mathcal {N}_{\infty }$
constructed at each successor stage
$\mathcal {N}_{\infty }$
constructed at each successor stage
![]() $ \alpha +1$
via a uet-forcing and any G-r-Tanaka sentence
$ \alpha +1$
via a uet-forcing and any G-r-Tanaka sentence
![]() $\Lambda $
, if
$\Lambda $
, if
![]() $ \mathcal {N}\vDash \lnot \Lambda $
then
$ \mathcal {N}\vDash \lnot \Lambda $
then
![]() $\mathcal {N}_{\infty }\vDash \lnot \Lambda $
.
$\mathcal {N}_{\infty }\vDash \lnot \Lambda $
.
Proof The argument for quantifier free sentences is as in Theorem 4.11 as are the inductive cases for
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
,
$\vee $
,
![]() $\exists x$
,
$\exists x$
,
![]() $\forall x$
, and
$\forall x$
, and
![]() $\forall X$
. We need to verify the claim for sentences of the form
$\forall X$
. We need to verify the claim for sentences of the form
![]() $\exists !Y\Phi (Y)$
for arithmetic
$\exists !Y\Phi (Y)$
for arithmetic
![]() $\Phi $
and
$\Phi $
and
![]() $\exists !Y\exists Z\Psi (Y,Z)$
with
$\exists !Y\exists Z\Psi (Y,Z)$
with
![]() $\Psi $
a
$\Psi $
a
![]() $\Sigma _{3}^{0}$
formula (each with constants for elements of N and
$\Sigma _{3}^{0}$
formula (each with constants for elements of N and
![]() $S(\mathcal {N})$
).
$S(\mathcal {N})$
).
Consider first one of the forms
![]() $\exists !Y\Phi (Y)$
for arithmetic
$\exists !Y\Phi (Y)$
for arithmetic
![]() $\Phi $
. If there are two Y in
$\Phi $
. If there are two Y in
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $\mathcal {N}\vDash \Phi (Y)$
then they also satisfy the same sentence in
$\mathcal {N}\vDash \Phi (Y)$
then they also satisfy the same sentence in
![]() $\mathcal {N}_{\infty }$
for the desired contradiction. So we assume there is no such Y in
$\mathcal {N}_{\infty }$
for the desired contradiction. So we assume there is no such Y in
![]() $\mathcal {N}$
while there is (exactly) one, say V, in
$\mathcal {N}$
while there is (exactly) one, say V, in
![]() $\mathcal {N}_{\infty }$
. So there is a least
$\mathcal {N}_{\infty }$
. So there is a least
![]() $\alpha $
such that
$\alpha $
such that
![]() $V\in \mathcal {N}_{\alpha +1}=\mathcal {N} _{\alpha }[G]$
. (We write G for
$V\in \mathcal {N}_{\alpha +1}=\mathcal {N} _{\alpha }[G]$
. (We write G for
![]() $G_{\alpha }$
for notational convenience.) Let
$G_{\alpha }$
for notational convenience.) Let
![]() $V=\Phi _{e}^{A\oplus G}$
for some
$V=\Phi _{e}^{A\oplus G}$
for some
![]() $A\in S(\mathcal {N}_{\alpha })$
and
$A\in S(\mathcal {N}_{\alpha })$
and
![]() $ v_{n}=V(n)$
.
$ v_{n}=V(n)$
.
We now take a
![]() $\left \langle \tau ,T\right \rangle $
in the generic filter for G (for the forcing used over
$\left \langle \tau ,T\right \rangle $
in the generic filter for G (for the forcing used over
![]() $\mathcal {N}_{\alpha }$
) such that
$\mathcal {N}_{\alpha }$
) such that
![]() $ \left \langle \tau ,T\right \rangle \Vdash \forall x(\Phi _{e}^{A\oplus G}(x)=0\vee \Phi _{e}^{A\oplus G}(x)=1)\wedge \Phi (\Phi _{e}^{A\oplus G})$
. For each n we have a
$ \left \langle \tau ,T\right \rangle \Vdash \forall x(\Phi _{e}^{A\oplus G}(x)=0\vee \Phi _{e}^{A\oplus G}(x)=1)\wedge \Phi (\Phi _{e}^{A\oplus G})$
. For each n we have a
![]() $\left \langle \tau _{n},T_{n}\right \rangle $
in the generic filter for G (and so wlog extending
$\left \langle \tau _{n},T_{n}\right \rangle $
in the generic filter for G (and so wlog extending
![]() $\left \langle \tau ,T\right \rangle $
) such that
$\left \langle \tau ,T\right \rangle $
) such that
![]() $\tau _{n}\Vdash \Phi _{e}^{A\oplus G}(n)=v_{n}$
. Much as in the proof of Theorem 4.5, if there is no
$\tau _{n}\Vdash \Phi _{e}^{A\oplus G}(n)=v_{n}$
. Much as in the proof of Theorem 4.5, if there is no
![]() $\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
and n such that
$\tau ^{\prime }\in Ext(\left \langle \tau ,T\right \rangle )$
and n such that
![]() $\tau ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(n)=1-v_{n}$
then
$\tau ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(n)=1-v_{n}$
then
![]() $V=\Phi _{e}^{A\oplus G}\in \mathcal {N}_{\alpha }$
for a contradiction. By the definition of uet-forcings we may choose
$V=\Phi _{e}^{A\oplus G}\in \mathcal {N}_{\alpha }$
for a contradiction. By the definition of uet-forcings we may choose
![]() $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
and
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
and
![]() $ m\geq n$
such that
$ m\geq n$
such that
![]() $|\tau _{m}|=|\tau ^{\prime }|=k>|\tau |$
. As
$|\tau _{m}|=|\tau ^{\prime }|=k>|\tau |$
. As
![]() $G\supseteq \tau _{m}$
is generic,
$G\supseteq \tau _{m}$
is generic,
![]() $G_{\tau ^{\prime }}$
is generic for the dense sets deciding all arithmetic formulas and so as
$G_{\tau ^{\prime }}$
is generic for the dense sets deciding all arithmetic formulas and so as
![]() $\left \langle \tau ,T\right \rangle $
is also in the filter for
$\left \langle \tau ,T\right \rangle $
is also in the filter for
![]() $G_{\tau ^{\prime }}$
,
$G_{\tau ^{\prime }}$
,
![]() $\mathcal { N}_{\alpha }[G_{\tau ^{\prime }}]\vDash \forall x(\Phi _{e}^{A\oplus G}(x)=0\vee \Phi _{e}^{A\oplus G}(x)=1)\wedge \Phi (\Phi _{e}^{A\oplus G})$
. As
$\mathcal { N}_{\alpha }[G_{\tau ^{\prime }}]\vDash \forall x(\Phi _{e}^{A\oplus G}(x)=0\vee \Phi _{e}^{A\oplus G}(x)=1)\wedge \Phi (\Phi _{e}^{A\oplus G})$
. As
![]() $G_{\tau ^{\prime }}$
differs from G by a finite set, it is also in
$G_{\tau ^{\prime }}$
differs from G by a finite set, it is also in
![]() $ \mathcal {N}_{\alpha }[G]=\mathcal {N}_{\alpha }[G_{\tau ^{\prime }}]=\mathcal { N}_{\alpha +1}$
. Thus in
$ \mathcal {N}_{\alpha }[G]=\mathcal {N}_{\alpha }[G_{\tau ^{\prime }}]=\mathcal { N}_{\alpha +1}$
. Thus in
![]() $\mathcal {N}_{\alpha +1}$
,
$\mathcal {N}_{\alpha +1}$
,
![]() $\Phi _{e}^{A\oplus G}=V^{\prime }$
and
$\Phi _{e}^{A\oplus G}=V^{\prime }$
and
![]() $\Phi _{e}^{A\oplus G}=V$
both exist, are different at
$\Phi _{e}^{A\oplus G}=V$
both exist, are different at
![]() $ n $
, and are witnesses for the arithmetic formula
$ n $
, and are witnesses for the arithmetic formula
![]() $\Phi (Y)$
. Thus they remain such in
$\Phi (Y)$
. Thus they remain such in
![]() $\mathcal {N}_{\infty }$
for a contradiction.
$\mathcal {N}_{\infty }$
for a contradiction.
We now turn to the case for
![]() $\Lambda $
of the form
$\Lambda $
of the form
![]() $\exists !Y\exists Z\Psi (Y,Z)$
for a
$\exists !Y\exists Z\Psi (Y,Z)$
for a
![]() $\Sigma _{3}^{0}$
formula
$\Sigma _{3}^{0}$
formula
![]() $\Psi $
. As in the previous case we have a least
$\Psi $
. As in the previous case we have a least
![]() $\alpha $
such that there is witness V for Y in
$\alpha $
such that there is witness V for Y in
![]() $\mathcal {N} _{\alpha +1}$
. If there is also a witness U for Z in
$\mathcal {N} _{\alpha +1}$
. If there is also a witness U for Z in
![]() $\mathcal {N} _{\alpha +1}$
then essentially the same argument as above (writing U as
$\mathcal {N} _{\alpha +1}$
then essentially the same argument as above (writing U as
![]() $ \Phi _{i}^{B,G}$
) shows that there are two distinct witnesses V and
$ \Phi _{i}^{B,G}$
) shows that there are two distinct witnesses V and
![]() $ V^{\prime }$
in
$ V^{\prime }$
in
![]() $\mathcal {N}_{\alpha +1}$
which have witness U and
$\mathcal {N}_{\alpha +1}$
which have witness U and
![]() $ U^{\prime }$
such that
$ U^{\prime }$
such that
![]() $\mathcal {N}_{\alpha +1}\vDash \Psi (X,V,U)\wedge \Psi (X,V^{\prime },U^{\prime })$
which again provides the contradiction to there being only one witness for Y in
$\mathcal {N}_{\alpha +1}\vDash \Psi (X,V,U)\wedge \Psi (X,V^{\prime },U^{\prime })$
which again provides the contradiction to there being only one witness for Y in
![]() $\mathcal {N}_{\infty }$
. On the other hand, as in the proof of Theorem 4.12, if there is no such
$\mathcal {N}_{\infty }$
. On the other hand, as in the proof of Theorem 4.12, if there is no such
![]() $ U$
in
$ U$
in
![]() $\mathcal {N}_{\alpha +1}$
then, for every k, the tree in
$\mathcal {N}_{\alpha +1}$
then, for every k, the tree in
![]() $\mathcal {N} _{\alpha +1}$
(recursive in V) associated with k being a witness for the
$\mathcal {N} _{\alpha +1}$
(recursive in V) associated with k being a witness for the
![]() $\Sigma _{3}^{0}$
formula
$\Sigma _{3}^{0}$
formula
![]() $\Psi $
has no branch in
$\Psi $
has no branch in
![]() $\mathcal {N}_{\alpha +1}$
. By Theorem 4.5.3 the nonexistence of a branch in any of these trees is propagated through the iteration and so V has no witness for Z in
$\mathcal {N}_{\alpha +1}$
. By Theorem 4.5.3 the nonexistence of a branch in any of these trees is propagated through the iteration and so V has no witness for Z in
![]() $\mathcal {N}_{\infty }$
for another contradiction.
$\mathcal {N}_{\infty }$
for another contradiction.
By our usual arguments, this theorem provides the further conservation results for all our principles as well as many others as corollaries.
Corollary 7.6. The following principles (and even their union) are all G-r-Tanaka (and hence G-Tanaka, G-r-
![]() $\Pi _{2}^{1}$
and G-
$\Pi _{2}^{1}$
and G-
![]() $\Pi _{1}^{1}$
) conservative over RCA
$\Pi _{1}^{1}$
) conservative over RCA
![]() $_{0}$
via extensions with forcings that omit branches (and so avoid cones):
$_{0}$
via extensions with forcings that omit branches (and so avoid cones):
![]() $\Sigma _{\infty }^{1}-AC^{\ast }$
(and all its consequences such as
$\Sigma _{\infty }^{1}-AC^{\ast }$
(and all its consequences such as
![]() $\Sigma _{\infty }^{1}-AC^{-}$
,
$\Sigma _{\infty }^{1}-AC^{-}$
,
![]() $\Sigma _{n}^{1}-AC^{\ast }$
, and
$\Sigma _{n}^{1}-AC^{\ast }$
, and
![]() $\Sigma _{n}^{1}-AC^{-}$
, SCR
$\Sigma _{n}^{1}-AC^{-}$
, SCR
![]() $_{XY}^{\ast }$
and SCR
$_{XY}^{\ast }$
and SCR
![]() $_{XY}^{-}$
), LF
$_{XY}^{-}$
), LF
![]() $_{XY}$
, COH, AMT,
$_{XY}$
, COH, AMT,
![]() $\Pi _{\infty }^{0}G$
(RCA
$\Pi _{\infty }^{0}G$
(RCA
![]() $_{0}^{+}$
), the existence of minimal covers for Turing reducibility and related theorems.
$_{0}^{+}$
), the existence of minimal covers for Turing reducibility and related theorems.
Proof We need only check that the et-forcings used or mentioned so far are actually uet-forcings. These checks are basically straightforward except for Sacks forcing. The version of Sacks forcing typically used to construct, for example, minimal covers is not uniform in our sense. This application as well as other similar results can, as is well known, be proven using uniform recursive (in a specific A) trees as conditions (as in [Reference Lerman19, Chapter VI]. That construction is then easily seen to be one with a uet-forcing.
The proof of the case for
![]() $\exists !Y\Phi (Y)$
in Theorem 7.5 essentially shows that if there is a
$\exists !Y\Phi (Y)$
in Theorem 7.5 essentially shows that if there is a
![]() $Y\in S(\mathcal {N}[G])-S(\mathcal {N})$
for a sufficiently generic G over a uet-forcing such that
$Y\in S(\mathcal {N}[G])-S(\mathcal {N})$
for a sufficiently generic G over a uet-forcing such that
![]() $\mathcal {N} [G]\vDash \Phi (Y)$
then there are at least two
$\mathcal {N} [G]\vDash \Phi (Y)$
then there are at least two
![]() $Z\in S(\mathcal {N}[G])$
such that
$Z\in S(\mathcal {N}[G])$
such that
![]() $\mathcal {N}[G]\vDash \Phi (Z)$
. We improve this to there being infinitely many. We then mention some applications of this improvement as well as that of going to G-Tanaka formulas that do not seem to follow from standard Tanaka conservativity.
$\mathcal {N}[G]\vDash \Phi (Z)$
. We improve this to there being infinitely many. We then mention some applications of this improvement as well as that of going to G-Tanaka formulas that do not seem to follow from standard Tanaka conservativity.
Proposition 7.7. If
![]() $\mathcal {N}\vDash RCA_{0}$
is countable,
$\mathcal {N}\vDash RCA_{0}$
is countable,
![]() $\mathcal {P}$
is a uet-forcing over
$\mathcal {P}$
is a uet-forcing over
![]() $\mathcal {N}$
, G is generic over
$\mathcal {N}$
, G is generic over
![]() $\mathcal {P}$
, and
$\mathcal {P}$
, and
![]() $\Theta (Y)$
is an arithmetic formula over
$\Theta (Y)$
is an arithmetic formula over
![]() $\mathcal {N}$
such that there is a
$\mathcal {N}$
such that there is a
![]() $Y\in S( \mathcal {N}[G])-S(\mathcal {N})$
for which
$Y\in S( \mathcal {N}[G])-S(\mathcal {N})$
for which
![]() $\mathcal {N}[G]\vDash \Theta (Y)$
then there is a sequence
$\mathcal {N}[G]\vDash \Theta (Y)$
then there is a sequence
![]() $\left \langle Y_{i}|i\in N\right \rangle \in S( \mathcal {N}[G])$
with the
$\left \langle Y_{i}|i\in N\right \rangle \in S( \mathcal {N}[G])$
with the
![]() $Y_{i}$
pairwise distinct such that
$Y_{i}$
pairwise distinct such that
![]() $\mathcal {N} [G]\vDash (\forall i)(\Theta (Y_{i}))$
. (Actually if one correctly defines the forcing relation for all second order sentences, essentially the same argument will work for arbitrary
$\mathcal {N} [G]\vDash (\forall i)(\Theta (Y_{i}))$
. (Actually if one correctly defines the forcing relation for all second order sentences, essentially the same argument will work for arbitrary
![]() $\Theta $
.)
$\Theta $
.)
Proof Suppose that the Y given by the proposition is
![]() $\Phi _{e}^{A\oplus G}$
for some
$\Phi _{e}^{A\oplus G}$
for some
![]() $e\in N$
and
$e\in N$
and
![]() $A\in S(\mathcal {N})$
and
$A\in S(\mathcal {N})$
and
![]() $\left \langle \tau ,T\right \rangle \Vdash \Theta (\Phi _{e}^{A\oplus G})$
. The argument in the proof of Theorem 7.5 shows that for any
$\left \langle \tau ,T\right \rangle \Vdash \Theta (\Phi _{e}^{A\oplus G})$
. The argument in the proof of Theorem 7.5 shows that for any
![]() $\sigma \subseteq G$
(and so
$\sigma \subseteq G$
(and so
![]() $\sigma \in Ext(\left \langle \tau ,T\right \rangle $
) there are
$\sigma \in Ext(\left \langle \tau ,T\right \rangle $
) there are
![]() $\sigma ^{\prime },\tau ^{\prime }\supseteq \sigma $
in
$\sigma ^{\prime },\tau ^{\prime }\supseteq \sigma $
in
![]() $Ext(\left \langle \tau ,T\right \rangle )$
,
$Ext(\left \langle \tau ,T\right \rangle )$
,
![]() $j\neq k$
and x such that
$j\neq k$
and x such that
![]() $\sigma ^{\prime }\subseteq G $
,
$\sigma ^{\prime }\subseteq G $
,
![]() $\sigma ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(x)=j$
and
$\sigma ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(x)=j$
and
![]() $\tau ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(x)=k$
. In
$\tau ^{\prime }\Vdash \Phi _{e}^{A\oplus G}(x)=k$
. In
![]() $\mathcal {N}[G]$
we can then recursively in G construct sequences
$\mathcal {N}[G]$
we can then recursively in G construct sequences
![]() $\sigma _{i},\tau _{i},x_{i},j_{i}$
, and
$\sigma _{i},\tau _{i},x_{i},j_{i}$
, and
![]() $k_{i}$
such that
$k_{i}$
such that
![]() $\sigma _{i}\subseteq \sigma _{i+1}\subseteq G$
,
$\sigma _{i}\subseteq \sigma _{i+1}\subseteq G$
,
![]() $ \sigma _{i}\subseteq \tau _{i}\in Ext(\left \langle \tau ,T\right \rangle )$
,
$ \sigma _{i}\subseteq \tau _{i}\in Ext(\left \langle \tau ,T\right \rangle )$
,
![]() $ \sigma _{i+1}\Vdash \Phi _{e}^{A\oplus G}(x_{i})=j_{i}$
, and
$ \sigma _{i+1}\Vdash \Phi _{e}^{A\oplus G}(x_{i})=j_{i}$
, and
![]() $\tau _{i}\Vdash \Phi _{e}^{A\oplus G}(x_{i})=k_{i}\neq j_{i}$
. We now claim that the sequence
$\tau _{i}\Vdash \Phi _{e}^{A\oplus G}(x_{i})=k_{i}\neq j_{i}$
. We now claim that the sequence
![]() $\Phi _{e}^{A\oplus G_{\tau _{i}}}$
is as desired. The argument in Theorem 7.5 shows that each of these is in
$\Phi _{e}^{A\oplus G_{\tau _{i}}}$
is as desired. The argument in Theorem 7.5 shows that each of these is in
![]() $\mathcal {N}[G]$
and satisfies
$\mathcal {N}[G]$
and satisfies
![]() $\Theta $
there. The construction guarantees that, for each i,
$\Theta $
there. The construction guarantees that, for each i,
![]() $ \Phi _{e}^{A\oplus G_{\tau _{i}}}(x_{i})=k_{i}\neq j_{i}=\Phi _{e}^{A\oplus G_{\sigma _{i+1}}}(x_{i})=\Phi _{e}^{A\oplus G}(x_{i})=\Phi _{e}^{A\oplus G_{\tau _{l}}}(x_{i})$
for every
$ \Phi _{e}^{A\oplus G_{\tau _{i}}}(x_{i})=k_{i}\neq j_{i}=\Phi _{e}^{A\oplus G_{\sigma _{i+1}}}(x_{i})=\Phi _{e}^{A\oplus G}(x_{i})=\Phi _{e}^{A\oplus G_{\tau _{l}}}(x_{i})$
for every
![]() $l>i$
. Thus the
$l>i$
. Thus the
![]() $\Phi _{e}^{A\oplus G_{\tau _{i}}}$
are pairwise distinct.
$\Phi _{e}^{A\oplus G_{\tau _{i}}}$
are pairwise distinct.
We now consider some generalizations of unique existence assertions to other cardinality quantifiers and applications to show that for such assertions we can also derive information about the existence of recursive solutions. (This is done in STY [Theorem 4.18] for unique existence for WKL
![]() $_{0}$
.)
$_{0}$
.)
We begin by formalizing the notions of “there are exactly,” “at least,” or “at most” m many Y such that
![]() $\Phi (Y) $
holds. In general,
$\Phi (Y) $
holds. In general,
![]() $\Phi $
can be arbitrary but we will restrict our attention to the arithmetic case for our applications. We are formalizing the definition of cardinality m that asserts the existence of a one–one correspondence with the natural numbers less than m in a way that works well in RCA
$\Phi $
can be arbitrary but we will restrict our attention to the arithmetic case for our applications. We are formalizing the definition of cardinality m that asserts the existence of a one–one correspondence with the natural numbers less than m in a way that works well in RCA
![]() $_{0}$
.
$_{0}$
.
Definition 7.8. We say that there are exactly m many Y such that
![]() $ \Phi (Y)$
,
$ \Phi (Y)$
,
![]() $(\exists ^{=m}Y)\Phi (Y)$
, if there is a pairwise distinct sequence
$(\exists ^{=m}Y)\Phi (Y)$
, if there is a pairwise distinct sequence
![]() $\left \langle Y_{i}|i<m\right \rangle $
such that
$\left \langle Y_{i}|i<m\right \rangle $
such that
![]() $(\forall i<m)\Phi (Y_{i})$
and
$(\forall i<m)\Phi (Y_{i})$
and
![]() $\forall W(\Phi (W)\rightarrow \exists i<m)((W=Y_{i}))$
. Note that, in RCA
$\forall W(\Phi (W)\rightarrow \exists i<m)((W=Y_{i}))$
. Note that, in RCA
![]() $_{0}$
, this is equivalent to the existence of a unique such sequence where the
$_{0}$
, this is equivalent to the existence of a unique such sequence where the
![]() $Y_{i}$
are in strict ascending lexicographic order. It is also worth pointing out that for
$Y_{i}$
are in strict ascending lexicographic order. It is also worth pointing out that for
![]() $m\in \mathbb {N}$
we can express this by a single formula not mentioning m. On the other hand, we can view m as a variable over the numbers N in any model of RCA
$m\in \mathbb {N}$
we can express this by a single formula not mentioning m. On the other hand, we can view m as a variable over the numbers N in any model of RCA
![]() $_{0}$
. This allows to express the quantifier there are finitely many Y such that
$_{0}$
. This allows to express the quantifier there are finitely many Y such that
![]() $ \Phi (Y)$
as
$ \Phi (Y)$
as
![]() $\exists m(\exists ^{=m}Y)(\Phi (Y))$
which we write as
$\exists m(\exists ^{=m}Y)(\Phi (Y))$
which we write as
![]() $ (\exists ^{Fin}Y)(\Phi (Y))$
. Similarly, we say
$ (\exists ^{Fin}Y)(\Phi (Y))$
. Similarly, we say
![]() $(\exists ^{\geq m}Y)\Phi (Y) $
or
$(\exists ^{\geq m}Y)\Phi (Y) $
or
![]() $(\exists ^{\leq m}Y)(\phi (Y))$
, if there is a pairwise distinct sequence
$(\exists ^{\leq m}Y)(\phi (Y))$
, if there is a pairwise distinct sequence
![]() $\left \langle Y_{i}|i<m\right \rangle $
such that
$\left \langle Y_{i}|i<m\right \rangle $
such that
![]() $(\forall i<m)\Phi (Y)$
or, respectively, if there is a pairwise distinct sequence
$(\forall i<m)\Phi (Y)$
or, respectively, if there is a pairwise distinct sequence
![]() $ \left \langle Y_{i}|i<m\right \rangle $
such that
$ \left \langle Y_{i}|i<m\right \rangle $
such that
![]() $\forall W(\Phi (W)\rightarrow \exists i<m)((W=Y_{i}))$
. Of course,
$\forall W(\Phi (W)\rightarrow \exists i<m)((W=Y_{i}))$
. Of course,
![]() $(\exists ^{=m}Y)\Phi (Y)\Leftrightarrow (\exists ^{\geq m}Y)\Phi (Y)~\&~(\exists ^{\leq m}Y)(\phi (Y))$
.
$(\exists ^{=m}Y)\Phi (Y)\Leftrightarrow (\exists ^{\geq m}Y)\Phi (Y)~\&~(\exists ^{\leq m}Y)(\phi (Y))$
.
We now give some applications.
Theorem 7.9. Let Q be any of the theories mentioned in this section (or combinations of them) which can be guaranteed to hold by iterating uet-forcings over any countable model
![]() $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
![]() $_{0}$
to produce a model
$_{0}$
to produce a model
![]() $\mathcal {N} _{\infty }$
of Q with the same first order part as
$\mathcal {N} _{\infty }$
of Q with the same first order part as
![]() $\mathcal {N}$
. Let
$\mathcal {N}$
. Let
![]() $ \Phi (Y)$
be any arithmetic formula of the pure second order language, i.e., lightfaced—with no parameters—and with its only free variable being Y and
$ \Phi (Y)$
be any arithmetic formula of the pure second order language, i.e., lightfaced—with no parameters—and with its only free variable being Y and
![]() $k\in \mathbb {N}$
be a standard number. Note that below by recursive we mean lightfaced
$k\in \mathbb {N}$
be a standard number. Note that below by recursive we mean lightfaced
![]() $\Delta _{1}^{0}$
.
$\Delta _{1}^{0}$
.
-
1. If
 $Q\vdash (\exists ^{Fin}Y)\Phi (Y)$
then RCA
$Q\vdash (\exists ^{Fin}Y)\Phi (Y)$
then RCA
 $_{0}\vdash (\exists ^{Fin}Y)\Phi (Y)$
.
$_{0}\vdash (\exists ^{Fin}Y)\Phi (Y)$
. -
2. If
 $Q\vdash (\exists ^{Fin}Y)\Phi (Y) \ \&~(\exists ^{\geq k}Y)\Phi (Y) $
then RCA
$Q\vdash (\exists ^{Fin}Y)\Phi (Y) \ \&~(\exists ^{\geq k}Y)\Phi (Y) $
then RCA
 $_{0}\vdash (\exists ^{Fin}Y)\Phi (Y) ~ \&~(\exists ^{\geq k}Y)(Y$
is recursive and
$_{0}\vdash (\exists ^{Fin}Y)\Phi (Y) ~ \&~(\exists ^{\geq k}Y)(Y$
is recursive and
 $\Phi (Y))$
.
$\Phi (Y))$
. -
3. If
 $Q\vdash (\exists ^{\leq k}Y)\Phi (Y)$
then RCA
$Q\vdash (\exists ^{\leq k}Y)\Phi (Y)$
then RCA
 $_{0}\vdash (\exists ^{\leq k}Y)\Phi (Y)$
.
$_{0}\vdash (\exists ^{\leq k}Y)\Phi (Y)$
. -
4. If
 $Q\vdash (\exists ^{=k}Y)\Phi (Y)$
then RCA
$Q\vdash (\exists ^{=k}Y)\Phi (Y)$
then RCA
 $_{0}\vdash (\exists ^{=k}Y)\Phi (Y)~\&~(\forall Y)(\Phi (Y)\rightarrow Y$
is recursive).
$_{0}\vdash (\exists ^{=k}Y)\Phi (Y)~\&~(\forall Y)(\Phi (Y)\rightarrow Y$
is recursive).
Proof For each assertion, suppose we have a countable
![]() $\mathcal {N}\vDash RCA_{0}$
which provides a counterexample to the desired conclusion. We argue for a contradiction to the associated hypothesis.
$\mathcal {N}\vDash RCA_{0}$
which provides a counterexample to the desired conclusion. We argue for a contradiction to the associated hypothesis.
-
1. Note that
 $(\exists ^{Fin}Y)\Phi (Y)$
is equivalent (in RCA
$(\exists ^{Fin}Y)\Phi (Y)$
is equivalent (in RCA
 $_{0})$
to
$_{0})$
to
 $ \exists m\exists !Z(Z$
is a sequence of sets
$ \exists m\exists !Z(Z$
is a sequence of sets
 $\left \langle Z_{i}|i<m\right \rangle $
in strictly ascending lexicographical order such that
$\left \langle Z_{i}|i<m\right \rangle $
in strictly ascending lexicographical order such that
 $(\forall i<m)(\Phi (Z_{i}))$
. As the formula in parentheses here is arithmetical (in m and Z), the whole assertion is a G-Tanaka sentence. Theorem 7.5 then guarantees that it and so
$(\forall i<m)(\Phi (Z_{i}))$
. As the formula in parentheses here is arithmetical (in m and Z), the whole assertion is a G-Tanaka sentence. Theorem 7.5 then guarantees that it and so
 $(\exists ^{Fin}Y)\Phi (Y)$
is a theorem of RCA
$(\exists ^{Fin}Y)\Phi (Y)$
is a theorem of RCA
 $_{0}$
as desired.
$_{0}$
as desired. -
2. We already have that RCA
 $_{0}\vdash (\exists ^{Fin}Y)\Phi (Y)$
and so we assume that we have a countable model
$_{0}\vdash (\exists ^{Fin}Y)\Phi (Y)$
and so we assume that we have a countable model
 $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
 $_{0}$
not containing k many recursive solutions to
$_{0}$
not containing k many recursive solutions to
 $\Phi $
. Let
$\Phi $
. Let
 $\mathcal {N}^{\prime }$
have the same first order part as
$\mathcal {N}^{\prime }$
have the same first order part as
 $\mathcal {N}$
and second order part
$\mathcal {N}$
and second order part
 $R( \mathcal {N})$
the collection of subsets of N which are recursive in
$R( \mathcal {N})$
the collection of subsets of N which are recursive in
 $ \mathcal {N}$
. Of course,
$ \mathcal {N}$
. Of course,
 $\mathcal {N}^{\prime }\vDash RCA_{0}$
as well but as
$\mathcal {N}^{\prime }\vDash RCA_{0}$
as well but as
 $\mathcal {N}$
and
$\mathcal {N}$
and
 $\mathcal {N}^{\prime }$
have the same first order part, they have the same recursive sets and so
$\mathcal {N}^{\prime }$
have the same first order part, they have the same recursive sets and so
 $\mathcal {N}^{\prime }\vDash \lnot \exists ^{\geq k}Y(\Phi (Y))$
. Now construct
$\mathcal {N}^{\prime }\vDash \lnot \exists ^{\geq k}Y(\Phi (Y))$
. Now construct
 $\mathcal {N}_{\infty }^{\prime }\vDash Q$
by an iteration beginning with
$\mathcal {N}_{\infty }^{\prime }\vDash Q$
by an iteration beginning with
 $\mathcal {N}^{\prime }$
. By our assumption, there are at least k many solutions Y for
$\mathcal {N}^{\prime }$
. By our assumption, there are at least k many solutions Y for
 $\Phi $
in
$\Phi $
in
 $ \mathcal {N}_{\infty }^{\prime }$
and so one not in
$ \mathcal {N}_{\infty }^{\prime }$
and so one not in
 $\mathcal {N}^{\prime }$
must appear for the first time at some
$\mathcal {N}^{\prime }$
must appear for the first time at some
 $\mathcal {N}_{\alpha +1}$
. Proposition 7.7 then guarantees that there is, in
$\mathcal {N}_{\alpha +1}$
. Proposition 7.7 then guarantees that there is, in
 $\mathcal {N} _{\alpha +1}$
and so in
$\mathcal {N} _{\alpha +1}$
and so in
 $\mathcal {N}_{\infty }$
, an infinite sequence
$\mathcal {N}_{\infty }$
, an infinite sequence
 $ \left \langle Z_{i}\right \rangle $
of solutions to
$ \left \langle Z_{i}\right \rangle $
of solutions to
 $\Phi $
for the desired contradiction to the assumption that
$\Phi $
for the desired contradiction to the assumption that
 $Q\vdash (\exists ^{Fin}Y)\Phi (Y)$
.
$Q\vdash (\exists ^{Fin}Y)\Phi (Y)$
. -
3. This one is simple. If we have a countable model
 $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
 $ _{0}$
with more than k many solutions Y for
$ _{0}$
with more than k many solutions Y for
 $\Phi $
then all of them are solutions in
$\Phi $
then all of them are solutions in
 $\mathcal {N}_{\infty }$
for a contradiction.
$\mathcal {N}_{\infty }$
for a contradiction. -
4. This follows directly from the previous cases.
If in the previous theorem and proof we consider formulas
![]() $\Phi (X,Y)$
with a free set variable X and assume that the hypotheses hold for the universal closure with respect to X, then so do the conclusions where we replace recursive by recursive in X.
$\Phi (X,Y)$
with a free set variable X and assume that the hypotheses hold for the universal closure with respect to X, then so do the conclusions where we replace recursive by recursive in X.
Acknowledgment
The author was partially supported by NSF Grant DMS-1161175.