We study the first-order consequences of Ramsey’s Theorem for k-colourings of n-tuples, for fixed 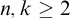 $n, k \ge 2$, over the relatively weak second-order arithmetic theory
$n, k \ge 2$, over the relatively weak second-order arithmetic theory 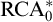 $\mathrm {RCA}^*_0$. Using the Chong–Mourad coding lemma, we show that in a model of
$\mathrm {RCA}^*_0$. Using the Chong–Mourad coding lemma, we show that in a model of 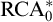 $\mathrm {RCA}^*_0$ that does not satisfy
$\mathrm {RCA}^*_0$ that does not satisfy 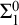 $\Sigma ^0_1$ induction,
$\Sigma ^0_1$ induction, 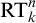 $\mathrm {RT}^n_k$ is equivalent to its relativization to any proper
$\mathrm {RT}^n_k$ is equivalent to its relativization to any proper 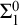 $\Sigma ^0_1$-definable cut, so its truth value remains unchanged in all extensions of the model with the same first-order universe.
$\Sigma ^0_1$-definable cut, so its truth value remains unchanged in all extensions of the model with the same first-order universe.
We give a complete axiomatization of the first-order consequences of 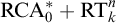 $\mathrm {RCA}^*_0 + \mathrm {RT}^n_k$ for
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_k$ for 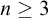 $n \ge 3$. We show that they form a non-finitely axiomatizable subtheory of
$n \ge 3$. We show that they form a non-finitely axiomatizable subtheory of 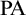 $\mathrm {PA}$ whose
$\mathrm {PA}$ whose 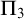 $\Pi _3$ fragment coincides with
$\Pi _3$ fragment coincides with 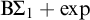 $\mathrm {B} \Sigma _1 + \exp $ and whose
$\mathrm {B} \Sigma _1 + \exp $ and whose 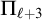 $\Pi _{\ell +3}$ fragment for
$\Pi _{\ell +3}$ fragment for 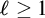 $\ell \ge 1$ lies between
$\ell \ge 1$ lies between 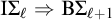 $\mathrm {I} \Sigma _\ell \Rightarrow \mathrm {B} \Sigma _{\ell +1}$ and
$\mathrm {I} \Sigma _\ell \Rightarrow \mathrm {B} \Sigma _{\ell +1}$ and 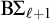 $\mathrm {B} \Sigma _{\ell +1}$. We also give a complete axiomatization of the first-order consequences of
$\mathrm {B} \Sigma _{\ell +1}$. We also give a complete axiomatization of the first-order consequences of 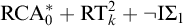 $\mathrm {RCA}^*_0 + \mathrm {RT}^2_k + \neg \mathrm {I} \Sigma _1$. In general, we show that the first-order consequences of
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_k + \neg \mathrm {I} \Sigma _1$. In general, we show that the first-order consequences of 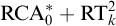 $\mathrm {RCA}^*_0 + \mathrm {RT}^2_k$ form a subtheory of
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_k$ form a subtheory of 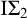 $\mathrm {I} \Sigma _2$ whose
$\mathrm {I} \Sigma _2$ whose 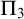 $\Pi _3$ fragment coincides with
$\Pi _3$ fragment coincides with 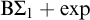 $\mathrm {B} \Sigma _1 + \exp $ and whose
$\mathrm {B} \Sigma _1 + \exp $ and whose 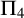 $\Pi _4$ fragment is strictly weaker than
$\Pi _4$ fragment is strictly weaker than 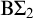 $\mathrm {B} \Sigma _2$ but not contained in
$\mathrm {B} \Sigma _2$ but not contained in 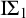 $\mathrm {I} \Sigma _1$.
$\mathrm {I} \Sigma _1$.
Additionally, we consider a principle 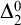 $\Delta ^0_2$-
$\Delta ^0_2$-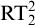 $\mathrm {RT}^2_2$ which is defined like
$\mathrm {RT}^2_2$ which is defined like 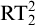 $\mathrm {RT}^2_2$ but with both the
$\mathrm {RT}^2_2$ but with both the 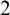 $2$-colourings and the solutions allowed to be
$2$-colourings and the solutions allowed to be 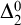 $\Delta ^0_2$-sets rather than just sets. We show that the behaviour of
$\Delta ^0_2$-sets rather than just sets. We show that the behaviour of 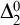 $\Delta ^0_2$-
$\Delta ^0_2$-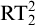 $\mathrm {RT}^2_2$ over
$\mathrm {RT}^2_2$ over 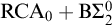 $\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$ is in many ways analogous to that of
$\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$ is in many ways analogous to that of 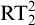 $\mathrm {RT}^2_2$ over
$\mathrm {RT}^2_2$ over 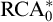 $\mathrm {RCA}^*_0$, and that
$\mathrm {RCA}^*_0$, and that 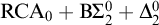 $\mathrm {RCA}_0 + \mathrm {B} \Sigma ^0_2 + \Delta ^0_2$-
$\mathrm {RCA}_0 + \mathrm {B} \Sigma ^0_2 + \Delta ^0_2$-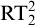 $\mathrm {RT}^2_2$ is
$\mathrm {RT}^2_2$ is 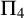 $\Pi _4$- but not
$\Pi _4$- but not 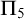 $\Pi _5$-conservative over
$\Pi _5$-conservative over 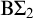 $\mathrm {B} \Sigma _2$. However, the statement we use to witness failure of
$\mathrm {B} \Sigma _2$. However, the statement we use to witness failure of 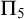 $\Pi _5$-conservativity is not provable in
$\Pi _5$-conservativity is not provable in 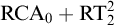 $\mathrm {RCA}_0 +\mathrm {RT}^2_2$.
$\mathrm {RCA}_0 +\mathrm {RT}^2_2$.
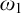 $\omega _1$
$\omega _1$
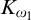 $ K_{\omega _1}$ AND
$ K_{\omega _1}$ AND 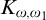 $K_{\omega ,\omega _1}$
$K_{\omega ,\omega _1}$