Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-12T22:58:54.709Z Has data issue: false hasContentIssue false
  • English
  • Français

The characterization of monadic logic

Published online by Cambridge University Press:  12 March 2014

Leslie H. Tharp
Leslie H. Tharp*
Affiliation:
Rockefeller University, New York, New York 10021
Get access Rights & Permissions [Opens in a new window]

Extract

The first section of this paper is concerned with the intrinsic properties of elementary monadic logic (EM), and characterizations in the spirit of Lindström [2] are given. His proofs do not apply to monadic logic since relations are used, and intrinsic properties of EM turn out to differ in certain ways from those of the elementary logic of relations (i.e., the predicate calculus), which we shall call EL. In the second section we investigate connections between higher-order monadic and polyadic logics.

EM is the subsystem of EL which results by the restriction to one-place predicate letters. We omit constants (for simplicity) but take EM to contain identity. Let a type be any finite sequence (possibly empty) of one-place predicate letters. A model M of type 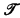has a nonempty universe ∣M∣ and assigns to each predicate letter P of 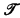a subset PM of ∣M∣.

Let us take a monadic logic L to be any collection of classes of models, called L-classes, satisfying the following:

1. All models in a given L-class are of the same type (called the type of the class).

2. Isomorphic models lie in the same L-classes.

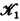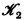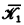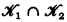3. If and are L-classes of the same type, then and are L-classes.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 38 , Issue 3 , September 1973 , pp. 481 - 488
Copyright
Copyright © Association for Symbolic Logic 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Tharp, Leslie H., The characterization of monadic logic, Notices of the American Mathematical Society, vol. 19 (1972), p. A–455. Abstract #72T-E42. (This abstract announces the results of §1 of the present paper.)Google Scholar
[2]Lindström, Per, On extensions of elementary logic, Theoria, vol. 35 (1969), pp. 1–11.CrossRefGoogle Scholar
[3]Lindström, Per, First order predicate logic with generalized quantifiers, Theoria, vol. 32 (1966), pp. 186–195.CrossRefGoogle Scholar
[4]Jensen, Ronald Bjorn, Ein neuer Beweisfür die Entscheidbarkeit des einstelligen Prädikatenkalküls mit Identität, Archiv für mathematische Logik und Grundlagenforschung, vol. 7 (1965), pp. 128–138.CrossRefGoogle Scholar
[5]Ackermann, Wilhelm, Solvable cases of the decision problem, North-Holland, Amsterdam, 1954.Google Scholar
[6]Lévy, Azriel, A hierarchy of formulas in set theory, Memoirs of the American Mathematical Society, No. 57, 1965.Google Scholar