Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T09:09:50.943Z Has data issue: false hasContentIssue false
  • English
  • Français

Definability and initial segments of c-degrees

Published online by Cambridge University Press:  12 March 2014

Robert S. Lubarsky
Robert S. Lubarsky*
Affiliation:
Department of Mathematics, Cornell University, Ithaca, New York 14853
Get access Rights & Permissions [Opens in a new window]

Abstract

We combine two techniques of set theory relating to mininal degrees of constructibility. Jensen constructed a minimal real which is additionally a 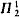singleton. Groszek built an initial segment of order type 1 + α*, for any ordinal α. This paper shows how to force a 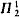singleton such that the c-degrees beneath it, all represented by reals, are of type 1 + α*, for many ordinals α. We also examine the definability α needs to be so represented by a real.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 4 , December 1988 , pp. 1070 - 1081
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

[A] Adamowicz, Zofia, Constructible semi-lattices of degrees of constructibility, Set theory and hierarchy theory. V (Lachlan, A. et al., editors), Lecture Notes in Mathematics, vol. 619, Springer-Verlag, Berlin, 1977, pp. 1–43.CrossRefGoogle Scholar
[G] Groszek, Marcia, in preparation.Google Scholar
[J] Jensen, Ronald, Definable sets of minimal degree, Mathematical logic and foundations of set theory (Bar-Hillel, Y., editor), North-Holland, Amsterdam, 1970, pp. 122–128.Google Scholar
[Le] Lerman, Manuel, Degrees of unsolvability. Springer-Verlag, Berlin, 1983.CrossRefGoogle Scholar
[Lu] Lubarsky, Robert, Lattices of c-degrees, Annals of Pure and Applied Logic, vol. 36 (1987), pp. 115–118.CrossRefGoogle Scholar
[Sa] Sacks, Gerald E., Countable admissible ordinals and hyperdegrees, Advances in Mathematics, vol. 20 (1976), pp. 213–262.CrossRefGoogle Scholar
[Sa1] Sacks, Gerald E., Forcing with perfect closed sets, Axiomatic set theory (Scott, D. S., editor), Proceedings of Symposia in Pure Mathematics, vol. 13, part 1, American Mathematical Society, Providence, Rhode Island, 1971, pp. 331–355.CrossRefGoogle Scholar