Article contents
Defining algebraic elements
Published online by Cambridge University Press: 12 March 2014
Extract
This paper is a survey and a synthesis of the various approaches to defining algebraic elements. Most of it is devoted to proving the following result.
Let T be a universal theory with the Amalgamation Property. Then for T the notions of algebraic element introduced by Robinson, Jónsson, and Morley are identical. Furthermore, they extend in a natural way the notion of algebraic element introduced by Park, and used by Lachlan and Baldwin and by Kueker.
In the course of proving this we shall construct the algebraic closure as a suitable injective hull and prove a unique factorisation theorem for algebraic predicates.
We shall also show (in §3) that if T is closed under products then algebraic elements all have degree 1. Thus in algebra, algebraic elements reduce to epimorphisms.
To demonstrate the remarkable stability of the notion we shall show (at the end of §5) that defining algebraic elements by infinitary formulas yields no new ones.
Let L be a language. The cardinality of the set of formulas of L is denoted by ∣L∣. An L-theory is a deductively closed set of L-sentences. We let 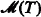 denote the category of models of T and (L-structure) homomorphisms between them. If A is a substructure of B we write A ≤ B. We call u: A → B an injection if u is an isomorphism of A with a substructure of B, and let
denote the category of models of T and (L-structure) homomorphisms between them. If A is a substructure of B we write A ≤ B. We call u: A → B an injection if u is an isomorphism of A with a substructure of B, and let 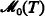 denote the subcategory of
denote the subcategory of 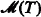 consisting of all injections.
consisting of all injections.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1973
References
REFERENCES
- 8
- Cited by

