Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-03-01T02:13:06.569Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTALITY RANK

Part of: Model theory

Published online by Cambridge University Press:  15 August 2022

ROLAND WALKER Open the ORCID record for ROLAND WALKER [Opens in a new window]
ROLAND WALKER*
Affiliation:
DEPARTMENT OF MATHEMATICS, STATISTICS, AND COMPUTER SCIENCE UNIVERSITY OF ILLINOIS AT CHICAGO 851 S MORGAN STREET, 322 SEO, MC 249 CHICAGO, IL 60607-7045, USA
*
E-mail: rwalke20@uic.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Building on Pierre Simon’s notion of distality, we introduce distality rank as a property of first-order theories and give examples for each rank m such that 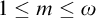$1\leq m \leq \omega $ . For NIP theories, we show that distality rank is invariant under base change. We also define a generalization of type orthogonality called m-determinacy and show that theories of distality rank m require certain products to be m-determined. Furthermore, for NIP theories, this behavior characterizes m-distality. If we narrow the scope to stable theories, we observe that m-distality can be characterized by the maximum cycle size found in the forking “geometry,” so it coincides with $(m-1)$ -triviality. On a broader scale, we see that m-distality is a strengthening of Saharon Shelah’s notion of m-dependence.

Keywords

model theoryclassification theorygeometric stability theoryindiscernible sequencesdependent theoriesrandom graphs

MSC classification

Primary: 03C45: Classification theory, stability and related concepts
Secondary: 03C52: Properties of classes of models
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 2 , June 2023 , pp. 704 - 737
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aschenbrenner, M., Chernikov, A., Gehret, A., and Ziegler, M., Distality in valued fields and related structures. Transactions of the American Mathematical Society, vol. 375 (2022), no. 7, 4641–4710. MR 4439488.CrossRefGoogle Scholar
Boxall, G. and Kestner, C., The definable $(p,q)$ -theorem for distal theories, this Journal, vol. 83 (2018), no. 1, pp. 123–127.Google Scholar
Chernikov, A., Galvin, D., and Starchenko, S., Cutting lemma and Zarankiewicz’s problem in distal structures. Selecta Mathematica, vol. 26 (2020), no. 2, Article no. 25, 27 pp.CrossRefGoogle Scholar
Chernikov, A. and Hempel, N., Mekler’s construction and generalized stability. Israel Journal of Mathematics , vol. 230 (2019), no. 2, pp. 745–769.CrossRefGoogle Scholar
Chernikov, A. and Hempel, N., On n-dependent groups and fields II. Forum of Mathematics, Sigma , vol. 9 (2021), Article no. e38, 51 pp.CrossRefGoogle Scholar
Chernikov, A., Palacin, D., and Takeuchi, K., On n-dependence. Notre Dame Journal of Formal Logic , vol. 60 (2019), no. 2, pp. 195–214.CrossRefGoogle Scholar
Chernikov, A. and Simon, P., Externally definable sets and dependent pairs II. Transactions of the American Mathematical Society , vol. 367 (2015), no. 7, pp. 5217–5235.CrossRefGoogle Scholar
Chernikov, A. and Starchenko, S., Regularity lemma for distal structures. Journal of the European Mathematical Society , vol. 20 (2018), no. 10, pp. 2437–2466.CrossRefGoogle Scholar
Chernikov, A. and Towsner, H., Hypergraph regularity and higher arity VC-dimension, preprint, 2020, arXiv:2010.00726.Google Scholar
Gehret, A. and Kaplan, E., Distality for the asymptotic couple of the field of logarithmic transseries. Notre Dame Journal of Formal Logic , vol. 61 (2020), no. 2, pp. 341–361.CrossRefGoogle Scholar
Goode, J. B., Some trivial considerations, this Journal, vol. 56 (1991), no. 2, pp. 624–631.Google Scholar
Hempel, N., On n-dependent groups and fields. Mathematical Logic Quarterly , vol. 62 (2016), no. 3, pp. 215–224.CrossRefGoogle Scholar
Hieronymi, P. and Nell, T., Distal and non-distal pairs, this Journal, vol. 82 (2017), no. 1, pp. 375–383.Google Scholar
Hodges, W., A Shorter Model Theory , Cambridge University Press, Cambridge, 1997.Google Scholar
Kaplan, I., Shelah, S., and Simon, P., Exact saturation in simple and NIP theories. Journal of Mathematical Logic , vol. 17 (2017), no. 1, Article no. 1750001, 18 pp.CrossRefGoogle Scholar
Marker, D., Model Theory: An Introduction, Graduate Texts in Mathematics, vol. 217, Springer, New York, 2002.Google Scholar
Marker, D., Model theory of valued fields. AMS Open Math Notes , 2019, OMN:201906.110798.Google Scholar
Nell, T., Distal and non-distal behavior in pairs. Mathematical Logic Quarterly , vol. 65 (2019), no. 1, pp. 23–36.CrossRefGoogle Scholar
Shelah, S., Strongly dependent theories. Israel Journal of Mathematics , vol. 204 (2014), no. 1, pp. 1–83.CrossRefGoogle Scholar
Shelah, S., Definable groups for dependent and 2-dependent theories. Sarajevo Journal of Mathematics , vol. 13(25) (2017), no. 1, pp. 3–25.Google Scholar
Simon, P., Distal and non-distal NIP theories. Annals of Pure and Applied Logic , vol. 164 (2013), no. 3, pp. 294–318.CrossRefGoogle Scholar
Simon, P., A Guide to NIP Theories, Lecture Notes in Logic, vol. 44, Association for Symbolic Logic and Cambridge Scientific, Cambridge, 2015.CrossRefGoogle Scholar
Simon, P., Type decomposition in NIP theories. Journal of the European Mathematical Society, vol. 22 (2020), no. 2, pp. 455–476.CrossRefGoogle Scholar
Tent, K. and Ziegler, M., A Course in Model Theory, Lecture Notes in Logic, vol. 40, Association for Symbolic Logic and Cambridge University Press, Cambridge, 2012.CrossRefGoogle Scholar
Terry, C., VCℓ-dimension and the jump to the fastest speed of a hereditary $\mathcal {L}$ -property. Proceedings of the American Mathematical Society, vol. 146 (2018), no. 7, pp. 3111–3126.CrossRefGoogle Scholar
Wilson, R. J., Introduction to Graph Theory, fourth ed., Longman, Harlow, 1996.Google Scholar